用于光学瞬变源搜寻的交叉证认快速算法*

徐 洋，吴 潮，万 萌，赵九鑫，田海俊，裘予雷，魏建彦，刘 勇

（1.三峡大学，湖北宜昌 443002；2.中国科学院国家天文台，北京 100012；3.香港科技大学，香港）

用于光学瞬变源搜寻的交叉证认快速算法*

徐 洋1，2，吴 潮2，万 萌2，赵九鑫3，田海俊1，2，裘予雷2，魏建彦2，刘 勇1

（1.三峡大学，湖北宜昌 443002；2.中国科学院国家天文台，北京 100012；3.香港科技大学，香港）

现代宽视场光学瞬变源巡天的大数据量特性和数据处理的高实时性要求，对利用星表交叉证认寻找瞬变源的方法提出了挑战。提出了一种基于等经纬分区建立空间索引的快速星表交叉证认算法。该算法通过对参考星表按相同经度和纬度间隔将视场所覆盖的天区划分为一个二维空间网格，并将二维网格直接与二维数组相对应，建立起星表的快速分区索引，从而实现处理速度的极大提升。算法的代码化测试结果为：对于天区覆盖为15°×15°记录条数为22万条的星表，在Intel Core i7 2600k CPU上的运行时间为0.3 s，比多级三角划分算法（Hierarchical Triangular Mesh，HTM）快34倍。测试结果表明该算法能很好地满足，如地面广角相机阵这样的大型宽场瞬变源巡天项目的数据处理实时性需求。同时详细地分析了算法中各个参数的意义和优化方法，并对算法的特点和适用范围进行了深入的讨论。

天文数据处理；交叉证认；等间隔分区；星表匹配；数组索引

光学瞬变源巡天的观测与研究是当今天文领域的一个前沿课题之一。比如美国在未来十年将重点支持的大型巡天望远镜（Large Synoptic Survey Telescope，LSST），其主要科学目标之一即为光学瞬变源的寻找［1］；我国正在兴建的地面广角相机阵（Ground Wide-Angle Camera，GWAC），其主要科学目标也是光学瞬变源（包括伽玛暴）的搜索。当前，从大视场的光学巡天观测中发现光学瞬变源的主要数据处理方法有：（1）通过直接的图像比较［2-3］（即图像相减的方法）获取残差图，然后分析残差图像找出瞬变天体目标。（2）通过直接的星表匹配方法［4-5］，将观测星表与已知的模板星表进行位置与流量的匹配，从而寻找出瞬变天体目标。这两种寻找瞬变源的方法各有优缺点，在实际使用过程中需要根据工程需求进行选取与优化。当前，对于LSST和GWAC这样大视场海量数据（LSST［6］：3.2 Giga-Pixel Image/10 s，GWAC：1.1 Giga-Pixel images/15 s）巡天项目寻找光学瞬变源所面临的最大挑战，无论是图像比较法还是星表模板匹配方法，都需要解决如何提高实时处理这些海量数据并找出瞬变源的速度问题。LSST项目目前正在尝试开发利用GPU进行图像比较方法的提速和开发机器学习算法对于瞬变源分类的实时自动处理。而对于GWAC项目，根据其数据特点，即低数据采样率，星表模板匹配方法更适合于光学瞬变源寻找的处理。星表模板匹配方法的速度瓶颈主要存在于星表的匹配计算（即交叉证认），因为在交叉证认过程中需要进行无数次的星表匹配计算。根据GWAC项目的实时性处理要求，对于一个GWAC星场（15°×15°）星数大约20万与同样星场的模板星表（星数约为20万）完成交叉证认所需要的时间必须在1 s之内，这对于传统的星表交叉证认算法的处理速度提出了一个挑战。

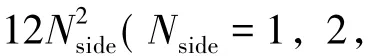
以上这些传统的交叉证认方法的研究主要在多波段天文学研究和数据挖掘中发挥着重要的作用，它们处理的数据对象是针对海量数据的交叉证认，处理的数据量级约为108到1010记录数，对星表相互交叉并无实时性处理要求。而对于瞬变源寻找的交叉证认则具有实时性要求并且数据量级在105左右。因此，对于如GWAC这样的瞬变源巡天项目，必须开展实时快速交叉证认算法的相关研究。

基于类似于GWAC这样的宽视场瞬变源巡天数据特点，即视场大约为200平方度，相互交叉星表的记录条数为20万条左右的数据，提出了一种基于等经纬分区的矩阵映射索引的实时快速交叉证认算法。本算法适用于宽视场瞬变源巡天中的瞬变源快速搜索需求，经过实际代码测试本算法能将以上数据的交叉证认时间控制在1 s之内。

本文主要通过算法的具体描述和算法的程序化实现与测试，表明本算法具有快速和高效的特点。在第2节，主要描述本算法的主要特征和具体过程，同时详细讨论算法的适用性和各参数的影响与选择；第3节，主要介绍算法的代码化和测试；最后一节，详细讨论了算法的特点和适用范围。

1 算法描述

算法的主要思想是通过等经纬分区将模板星表按所在天区的位置坐标即经、纬度划分为若干个相同经度和相同纬度间隔的空间二维矩阵，然后将这一矩阵映射到内存的二维数组，使得数组的每个元素与二维矩阵的每个单元格之间建立对应关系，从而建立起快速的寻址索引。由于采用经纬度的等间隔分区，使得索引建立过程的计算量大大减少，同时，通过数组索引又使得数据的搜索过程大大加快，从而实现整个交叉证认过程的加速。通过实验和分析表明在对于观测视场为200平方度左右的宽场巡天数据，本算法比较三角划分法（HTM）和多级等面积同赤纬划分法（HEALPix）等经典的分区法，在分区和建立索引的运算速度上具有优势。但等经纬分区的每个网格球面积与赤纬值有很大的依赖关系，尤其在极区附近较为显著，本算法对于这一因素所带来的影响进行了详细的分析，经过必要的分析和分段处理，妥善地解决了这个问题，使算法在速度和可靠性上都有了保证。

算法的处理流程如图1，主要过程包括（1）对模板星表建立分区索引。（a）对模板星表按赤经和赤纬划分为等间隔分区网格（二维分区网格）；（b）等间隔分区网格与内存数组建立映射关系；（2）星表查询。根据观测目标星的位置，查询所有相关的邻近网格，并搜索出所有相关网格的参考星；（3）匹配计算。对搜索得到的所有相关邻近参考星与观测目标星进行距离匹配计算。

1.1 建立模板星表的分区索引

建立模板星表分区索引的大致过程为：首先，扫描模板星表找出赤经、赤纬的最大值和最小值；然后，按间隔距离d（单位为度）分别在赤经和赤纬方向上将星表天区分为等间隔的分区网格。从而，建立起一个拥有M×N个网格数的空间二维分区网格，网格间距为d。最后，在计算机内存中开辟一个M×N的二维数组，将这个二维数组与空间二维网格建立起映射关系，从而实现分区网格的快速索引过程。

图1 快速交叉证认算法流程图Fig.1 Flowchart of the fast cross-identification algorithm

1.1.1 模板星表分区

模板星表分区即要实现将模板星表所在天区覆盖区域按等经度和等纬度间隔划分为M×N的空间网格（二维矩阵）。如图2，将模板星表中的赤经、赤纬的最大和最小值用 Rαmax，Rαmin，Decmax，Decmin表示，图中A、B、C、D代表模板星表所覆盖天区的4个顶点，按等距离d，将这一天区分解为M×N的空间二维网格。分区的赤经方向上的网格数M和赤纬方向的网格数N分别由下式计算给出：

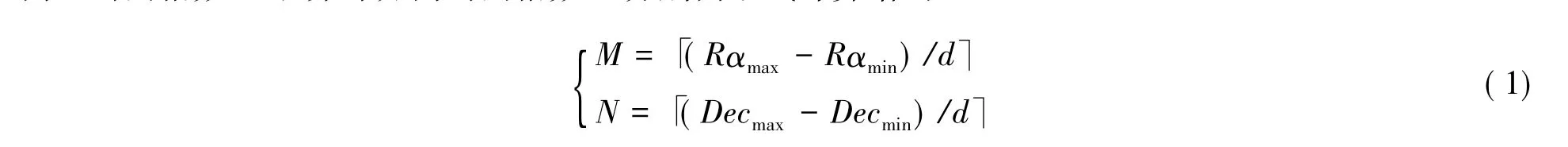
式中，“「⌉”为向上取整算符。分区网格按照从左到右、从下到上依次递增的方式进行编码，分区网格在矩阵网格中的坐标取值范围为（0，0）到（M-1，N-1），图中C点对应的分区坐标为（0，0），B点对应的分区坐标为（M-1，N-1）。

对于相同距离间隔d的分区网格在天球上的面积大小与所在的赤纬数值有很强的依赖关系，即对于相同的距离间隔d，在极区的覆盖面积会大大小于在赤道附近的面积。如果分区间隔d选取不适当，会导致分区面积过大或者过小从而影响计算的速度。因此，对于每个模板星表都需要首先分析该模板星表中心视场的赤纬值，从而决定分区间隔d的取值大小。

图2 星表等间隔分区图Fig.2 Illustration of the partition of the sky coverage of an object catalog with equal intervals

根据模板星表视场中心的赤纬值，天区的划分优化如下：

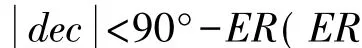
（2）间隔距离d的优化选择：d的取值大小会决定分区网格面积的大小和建立映射过程中开辟内存数组的大小而影响计算机资源的消耗情况。因此在实际使用中，需要根据不同情况处理d值的选取：星表天区在高纬度区域、面积较大或内存较小时，d的取值应偏大；反之星表天区在低纬度区域、面积较小或内存较大时，d的取值应偏小，但是应保证d的值＞ER。关于分区间隔d对计算性能的影响在后面的程序测试中会给出详细测试结果。

1.1.2 建立分区索引

将模板星表中的参考星按空间二维网格分区后与二维数组建立映射关系，从而建立起星表的分区索引。模板星表中的参考星（ra_r，dec_r）在二维分区网格中的坐标可由下面计算公式得出：

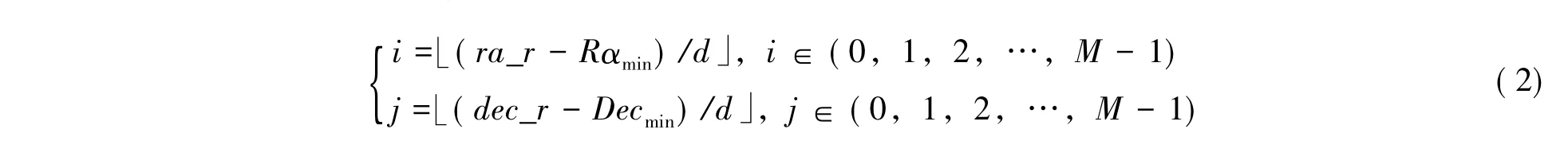
1.2 星表查询

星表的查询过程即要实现根据观测星表中的目标星位置（ra_t，dec_t），查询出所有与目标星邻近的参考星。实现过程如图3。首先，根据目标星位置（ra_t，dec_t）计算出所有相关邻近空间网格；然后，计算这些网格在二维分区网格中的坐标（i，j）；最后，通过坐标（i，j）查询出二维数组中所有对应位置的参考星。

图3 星表查询流程图Fig.3 Flowchart of a search in an object catalog

1.2.1 计算观测目标星的所有邻近匹配网格

查找观测目标星的邻近分区网格即为计算以目标星位置为中心，以星表总相关交叉误差半径（ER）为半径的圆所覆盖的所有网格。目标星邻近匹配网格的分布如图4，黑色点代表观测目标星，半径为ER的圆代表观测目标星的匹配区域，左边四幅图为远离极区时的匹配区域分布，第5幅图代表靠近极区时的匹配区域分布。由图4可知，由于天球坐标的球面特性，在以观测目标星为中心以ER为半径的球面覆盖，对于不同纬度的等经纬分区网格的范围是不同的。为保证没有查询遗漏，对于如何计算邻近匹配网格需要进行如下的分析与讨论。

图4 匹配区域各分布情况图Fig.4 Various cases of overlapping of sky interval（s）by a circular search area

如图5，P（ra，dec）为观测目标星的位置，虚线所示圆环为总交叉相关误差半径ER的覆盖区域，θ和α分别表示在赤纬与赤经方向的半径跨度。根据天体球面坐标系的特性，在赤纬方向半径跨度为：θ=ER，与所在赤纬值的大小无关。而在赤径方向上的半径跨度α则和所在赤纬值有相关性，用公式表示如下（由大圆距离公式［17］推导而来）：

为进一步研究各变量的相互关系，图6给出了α与θ和dec的相关关系，其中图6（a）的各曲线表示θ（等于ER）分别为2″～25″时，α与dec的关系，图6（b）则表示对不同θ，α（dec）与α（dec= 0°）的比率随赤纬变化关系。从图6（b）看出所有不同θ的α比率曲线都在同一条曲线上，这表明α比率与θ值无关。分析图6可以看出，当赤纬小于60°时，α的变化比较平缓（α（dec=60°）的值约为α（dec=0°）的值的两倍），当赤纬＞60°时，α的值急剧增大，为了避免多次计算α值对程序性能的影响，且兼顾极区的情况，可以分段对α进行取值：

图5 以总交叉误差为半径（ER）的圆在天球上的覆盖图

Fig.5 Coordinates and extended angles of a circle of radius ER on the celestial sphere

考虑到dec沿赤纬方向的变化，如图6，实际使用时为保证搜索的完整性，将dec=dec_C+ER代入以上各式，各种情况下的计算可归纳如下：

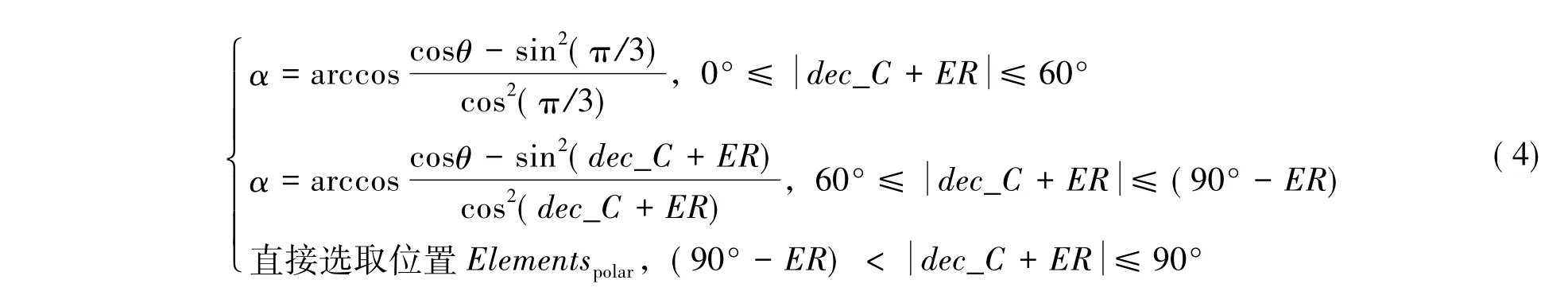
图6（a）赤经跨度α值与不同的赤纬跨度θ值的关系曲线图；（b）赤经跨度α值的比率与赤纬值的相关曲线图Fig.6（a）The relations ofαvs.Declination for different values ofθ；（b）The ratio ofα to the equatorial value vs.Declination

1.2.2 提取邻近匹配网格中的参考星数据

当观测目标星位置为（ra，dec）时，根据天球坐标特性取θ=ER，同时由（4）式可计算出α的值。由θ和α即可计算出匹配网格坐标it和jt，计算公式如下：

索引坐标为（it，jt），根据it和jt的整数的取值范围，即可通过排列组合得出所有邻近匹配网格坐标，同时，如果α＞90°-ER，则需要另加一个网格Elementspolar。根据这些匹配网格索引地址，即可快速提取出地址所对应的参考星数据。

1.3 匹配计算

将提取出来的所有参考星与观测目标星依次计算大圆距离，若第i颗参考星的大圆距离Lt为所有大圆距离中的最小值，且Lt小于误差半径ER，则认为第i颗参考星与目标星匹配成功，即完成该目标星的交叉证认。然后进行下一颗观测目标星的参考星搜索和匹配过程。

2 程序实现及性能测试

基于星表天区的等间隔分区特性，程序直接使用二维数组存储星表的二维矩阵网格信息，同时网格中的星以链表形式线性存储。如图7为程序的处理流程，图中星表A为模板星表链表（S1、S2、S3…代表星），星表B为观测目标星表链表，中间为分区索引数组（A1、A2、A3…代表分区网格）。

程序的实现过程：

（1）如图7中过程①，建立分区索引。程序通过扫描模板星表确定星表天区的边界，对天区在赤经和赤纬上按间隔d进行分区，并用二维数组存储分区索引，同时对极区情况单独申请一个存储空间，用于索引极区中的参考星。

（2）如图7中过程②，依次计算观测星表中每颗目标星的匹配网格集。计算匹配网格集是一个计算密集型过程，第2.2.1小节已讨论一部分优化方案，为进一步提升程序性能，可在程序运行之初，根据模板星表的赤纬的最大值和最小值，采用（4）式建立一个赤纬间隔为ER的α值索引，这样在程序运行过程中，可通过观测目标星匹配区域的最大赤纬值dec+θ直接查询α的值，无需对每个观测目标星都计算一次α值，这种方式在数据量较大时，性能提升尤为明显。

（3）如图7中过程③，匹配计算。依次根据目标星的匹配网格集中的网格索引，查找模板星表二维分区网格中的对应网格，并与网格中的所有星进行匹配计算，找出匹配距离最小的星，如果该距离小于ER，则认为这两颗星匹配成功。

图7 快速星表匹配算法程序处理过程Fig.7 The processing of the fast cross-identification algorithm

基于Intel Core i7 2600k CPU对本算法和HTM算法进行性能测试对比，针对HTM算法的测试主要基于HTM库［18］和DIF库［19］，其中HTM库中包含HTM算法的基本分区过程实现（包括分区编号的生成），DIF库中包含针对HTM算法的目标星邻近分区查找函数实现。同时选取位置测量误差20″作为ER的取值。

结合前文多方面的优化措施及精确邻近网格计算过程，本算法在面向GWAC类似的交叉证认需求时表现出优异的性能及匹配精度。具体测试结果如表1、表2、表3和表4，表中分区时间为模板星表建立分区索引所需的时间，计算时间包括查询分区网格和匹配计算所需的时间，总时间为分区时间和计算时间之和。

表1和表2分别为本算法在10万个分区网格和HTM算法在分区递归深度为10时，对不同规模数据在匹配过程中的分区时间、计算时间及总时间的统计。对比表1和表2可以得出，无论是分区时间还是计算时间，本算法在速度上有明显的优势，在GWAC类似规模的22万条星表记录匹配时，本算法比HTM算法快34倍。

表3为本算法在不同分区个数下针对22万条星表记录的详细性能测试。从表3可以看出，随着分区的增多，分区大小d的取值逐渐减少，总时间是逐渐减少的。在分区数为60万个时，分区大小d=45″，大于星表总相关交叉误差半径ER的20″，因而在d＞ER时，可以进一步增加分区个数，以获得匹配速度的提升。在分区大小d＞ER时，增加分区个数之所以能够提升程序性能，是因为分区个数的增加使每个分区中的参考星个数减少，即通过分区直接排除了不相关的参考星，从而匹配计算（计算大圆距离）的次数减少，达到程序性能的提升。在程序的内存消耗方面，60万个分区所占用的内存空间大约为10MB，这对目前GB级别的内存基本没有影响。考虑到对计算机资源的合理利用，在程序性能满足需求时，分区个数不应该大于模板星表的记录数，比如对22万条星表记录，推荐分区个数为10万到20万个。

表1 本算法在10万分区网格数时的不同数据量的运行时间表Table 1 The performance of our algorithm in searching catalogs of various object numbers w ith a fixed grid consisting of 100 000 intervals

表2 HTM算法在分区递归深度为10时的不同数据量的运行时间表Table 2 The performance of the HTM algorithm in searching catalogs of various object numbers w ith a fixed recursion depth of 10

表3 本算法在22万条星表记录时的不同分区数的运行时间对比Table 3 The performance of our algorithm in searching a catalog of 220 000 records w ith various grid-interval numbers

表4为HTM算法在不同分区递归深度下针对22万条星表记录的详细性能测试。HTM算法为全天区分区算法，如果按照全天区方式存储分区索引（可与数组建立线性映射关系，索引速度快），则在递归深度为12时，总分区个数为1.34亿个，分区索引信息需要占用2 GB的内存空间，此时的有效分区（分区中参考星个数大于等于1个）个数仅为4万个，分区利用率极低，而且递归深度每加1，占用的内存空间就会增大四倍。为减少分区索引所占用的内存空间，以在有限内存下对HTM算法在不同分区递归深度的性能进行测试，测试程序采用线性链表只存储有效分区，在递归深度为12时，索引信息仅占用内存1.3MB。从表中可以看出，总时间随着递归深度增加先减少后增加，在递归深度为10时达到最优的性能。导致该现象的原因是：分区个数随着递归深度的增加呈指数增加，而每个分区索引号的计算都需要通过多次递归计算得到，计算复杂，因而分区时间也呈指数增加。

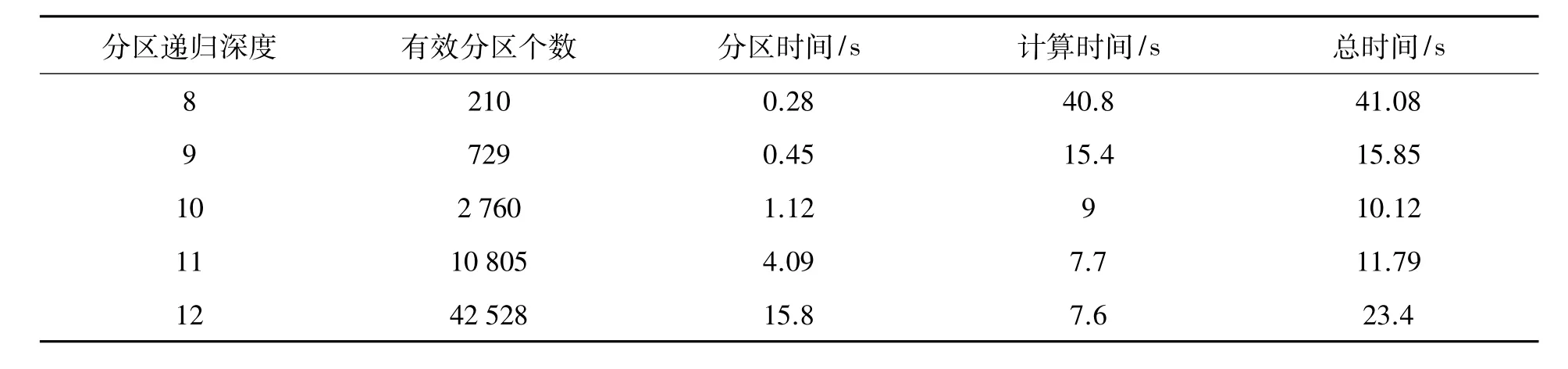
表4 HTM算法在22万条星表记录时的不同分区递归深度的运行时间对比Table 4 The performance of the HTM algorithm in searching a catalog of 220 000 recordsw ith various recursion-depth values

3 讨论与总结

为满足实时寻找瞬变源的交叉证认需求，本文提出了一个基于等经纬分区的矩阵映射索引的实时快速交叉证认算法。该算法对星表天区在赤经赤纬方向上按等间隔进行划分，将划分后的空间网格与二维数组间建立映射关系，实现分区的快速索引。本算法的分区索引建立过程和邻近分区的查找过程，相比传统分区算法计算复杂度大大降低，从而实现交叉证认过程的大幅提速。对于天区覆盖为15°× 15°记录条数为22万条的星表，在Intel Core i7 2600k CPU上的运行时间为0.3 s，相比HTM算法提速约34倍。

本算法在根据观测目标星位置搜索邻近网格区域的查询上，采用随着观测目标星赤纬值的变化，动态调整赤经方向的跨度α值，从而有效保证算法对不同赤纬天区的适用范围，克服了由于等经纬分区对于不同纬度时分区面积的不均匀性而导致的查询遗漏问题。同时，本算法所涉及的另一参数分区间隔d的大小直接影响算法的计算速度。d的取值大小影响每个网格天区面积的大小和总网格数的多少。d值越小则每个网格所覆盖的天区面积越少，意味着空间定位程度越高，最后被筛选剩下的参数与匹配的星数也就越小，从而会提高运算速度，但总网格数会增大又会增加计算机资源的消耗情况，而降低运算速度，反之亦然。为保证因分区网格过小导致出现过多无星的空网格而消耗计算机资源，分区间隔参数d必须大于星表总相关交叉误差半径ER。考虑上述因素的平衡关系，一般来说在计算机资源足够的情况下，d取3倍的总交叉误差半径较为合适。

本算法主要针对宽场瞬变源巡天的快速实时处理而开发，相对于传统的应用广泛的HTM和HEALpix算法，主要是在星表的分区过程和观测目标星的邻近匹配网格查找过程等方面根据实际需要进行了改进。（1）本算法采用等经纬间隔方式分区，分区形状在数值上表现为矩形网格，通过单步除法运算即可确定各分区范围；而HTM算法的分区形状为球面三角形，HEALpix算法的分区形状为曲线组成的等面积四边形，都要通过多次递归逐步分割天区。（2）基于等经纬间隔的矩形网格，只需根据观察目标星的邻近匹配区域在赤经赤纬方向上的跨度值进行单步除法运算，即可确定其邻近匹配网格；而HTM和HEALpix算法的该过程仍然需要递归运算，同时计算邻近匹配区域所覆盖的分区网格（球面三角形或不规则四边形）过程复杂度高。

本交叉证认算法适合于宽场光学瞬变源的实时搜索处理，如GWAC项目和我国南极的CSstar项目都可适用，同时也适用于这些项目的时序测光需要，因为通过筛选非匹配星可以找出瞬变源，而通过匹配星则可将同一星放在一块得到测光序列。算法的实际测试表明本算法的速度能很好地满足GWAC项目的工程需求。本算法对于天区的覆盖面积约束为100平方度～200平方度。对于更大天区的星表匹配，随着天区赤纬跨度的增大，分区面积差异和α值的差异会急剧增大，从而带来严重的性能问题。将来在处理更大天区和更大数据量的星表交叉证认时，可选用GPU并行方案，将模板星表和观测目标星表同时进行等间隔分区操作，将编号相同的参考分区网格和观测目标分区网格交由GPU上的同一线程处理，不同的分区由不同线程处理，这样在大量线程的同时并行处理下，程序的吞吐率会得到质的提高，从而为将来的算法移植和改进提供一个途径和研究方向。

［1］LSST［EB/OL］.［2012-11-3］.http：//www.lsst.org/lsst/science/scientist_transient.

［2］Alard C.Image subtraction using a space-varying kernel［J］.Astronomy and Astrophysics Supplement，2000，144：363-370.

［3］Bramich D M.A new algorithm for difference image analysis［J］.Monthly Notices of the Royal Astronomical Society，2008，386（1）：77-81.

［4］BhattiW A，Richmond MW，Ford H C，et al.Variable point sources in sloan digital sky survey stripe 82［J］.The Astrophysical Journal Supplement，2010，186（1）：233-258.

［5］Telezhinsky I，Eckert D，Savchenko V，et al.The catalog of variable sources detected by INTEGRAL［J］.Astronomy and Astrophysics，2010，522（1）：280-295.

［6］Vestrand ThomasW.Hot-wiring the Transient Universe［EB/OL］.［2012-11-03］.http：//www.cacr.caltech.edu/hotwired2/book/chapters/Introduction.pdf.

［7］Clive Page.Cross-matching Catalogues：Proposed Implementation［EB/OL］.［2012-11-03］.http：//wiki.astrogrid.org/pub/Astrogrid/DataDocs/crossmatch.htm l.

［8］Szalay A，Gray J，Fekete G，et al.Indexing the sphere with the hierarchical triangular mesh［J］.ARXIV，2007：arXiv：cs/0701164.

［9］Gorski K M，Wandelt B D，Hansen F K，et al.The HEALPix Primer［J］.ARXIV，1999： arXiv：astro-ph/9905275.

［10］Gray J，M A Nieto-Santisteban，A Szalay.The zones algorithm for finding points-near-a-point or cross-matching spatial datasets［J］.ARXIV，2006：arXiv：cs/0701171.

［11］Gray J，Szalay A S，Nieto-Santisteban M A，et al.There goes the neighborhood：relational algebra for spatial data search［J］.ARXIV，2004：arXiv：cs/0408031.

［12］ Nieto-Santisteban M A，Thakar A R，Szalay A S.Cross-matching very large data-sets［J］.Johns Hopkins University，Baltimore，2006.

［13］ 高丹，张彦霞，赵永恒.海量多波段星表数据的交叉证认的实现［J］.天文研究与技术——国家天文台台刊，2005，2（3）：186-193.Gao Dan，Zhang Yanxia，Zhao Yongheng.The realization of cross-identification based on huge multi-wavelength catalog data［J］.Astronomical Research＆ Technology——Publications of National Astronomical Observatories of China，2005，2（3）：186-193.

［14］ 高丹.海量天文数据融合系统的开发与数据挖掘算法的研究［D］.北京：中国科学院国家天文台，2008.

［15］Zhao Qing，Sun Jizhou，Yu Ce，et al.A paralleled large-scale astronomical cross-matching function［C］//Proceedings of the 9thInternational Conference on Algorithms and Architectures for Parallel Processing.Berlin：Springer，2009：604-614.

［16］ 赵青，孙济洲，肖健，等.基于MapReduce模型的分布式天文交叉证认［J］.计算机应用研究，2010，27（9）：3322-3325.Zhao Qing，Sun Jizhou，Xiao Jian，et al.Distributed astronomical cross-match based on MapReducemodel［J］.Application Research of Computers，2010，27（9）：3322-3325.

［17］ Great Circle Distance［EB/OL］.［2012-11-03］.http：//en.wikipedia.org/wiki/Great-circle_ distance.

［18］ HTM库［EB/OL］.［2012-11-03］.http：//www.skyserver.org/htm/.

［19］ DIF库［EB/OL］.［2012-11-03］.http：//ross.iasfbo.inaf.it/dif/.

A Fast Cross-Identification Algorithm for Searching Optical Transient Sources

Xu Yang1，2，Wu Chao2，Wan Meng2，Zhao Jiuxin3，Tian Haijun1，2，Qiu Yulei2，Wei Jianyan2，Liu Yong1
（1.Department of Computer Science and Technology，University of Three Gorges of China，Yichang，443002，China，Email：yxuctgu@gmail.com；2.National Astronomical Observatories，Chinese Academy of Sciences，Beijing 100012，China；3.University of Science＆Technology of Hong Kong）

With the development of modern wide-field optical transient（OT）surveys，the traditional methods of cross identification are facing a great challenge in real-time search of OT sources from data of large volumes.To overcome the difficulties encountered by the traditionalmethods，we propose a novel algorithm to speed up the search.This algorithm divides the sky coverage of the object catalog into a grid of regionswith a constant size in both Right-Ascension（RA）and Declination（Dec）directions.Ituses a fastapproach to index the grid regions，and maps them into a two-dimensional array in the computermemory.Our tests show that it takes the algorithm 0.3 seconds to perform cross identification in a catalog of 220 000 records if run on a computer of an Intel Core i7 2600k CPU.This is about34 times faster than the HTM algorithm.This indicates that our algorithm can meet the requirements on fast real-time OT-source search in a modern wide-field OT survey project，such as the Chinese Ground Wide-Angle Camera（GWAC）project.We also explain in detail the parameters of the functions of the algorithm and specify the optimal values of the parameters.We finally discuss the scope of applications and certain features of the algorithm.

Astronomical data processing；Cross identification；Division with even intervals；Catalog cross identification；Array indexing

TP302

：A

：1672-7673（2013）03-0273-10

国家自然科学基金（10903010）；国家自然科学天文联合基金（U1231123）；三峡大学启动经费（KJ2011B069）；三峡大学研究生科研创新基金（2011CX050）资助.

2012-11-16；修定日期：2012-12-26

徐 洋，男，硕士.研究方向：高性能计算.Email：yxuctgu@gmail.com

CN 53-1189/P ISSN 1672-7673