在近距双星系统中同步双星达到轨道圆形化时的轨道和自转演化的数值解和演化趋势
李林森
(东北师范大学物理学院,吉林长春 130024)
在近距双星系统中同步双星达到轨道圆形化时的轨道和自转演化的数值解和演化趋势
李林森
(东北师范大学物理学院,吉林长春 130024)
从非同步自转双星的轨道和自转的演化方程组推出同步双星的轨道和自转的演化方程组。用数值积分法给出演化方程组的数值解。计算同步自转双星EKCep达到轨道圆形化的时间和那时的轨道半长轴、轨道偏心率和主星自转角速度的演变数值。最后对轨道和自转的演化趋势做了推论。
同步自转双星EKCep;轨道圆化时间;轨道和自转;数值解
潮汐摩擦在近距双星系统中对轨道和自转的演化伴有重要角色。文[1-2]利用能量和角动量的方法研究了在近距双星系统中潮汐平衡和演化问题,但他的研究较少涉及轨道和自转的同步性。自转同步性的一系列研究首先是由文[3-4]完成的。文[5]研究了主序前收缩星晚型星的轨道圆形化问题并给出了数值结果。近年来,也有不少学者对双星自转和同步性的观测和理论研究做了工作。例如:文[6-8]等作者对双星自转的观测和同步性做了大量工作,特别对大陵五型双星的自转和同步性的统计观测。文[9]给出了判断双星同步自转的一种新方法。文[10-11]研究了非同步转动双星的轨道和自转的演化。文[12]给出了判断双星自转同步性的表象描述法。文[13]研究了太阳型双星的同步性观测。文[14]在文[12]的研究基础上又给出了判断分光双星自转同步性的方法。
作者在文[15]用分析法研究了在主序上轨道偏心率较小的同步双星(β-Per)的轨道和自转演化的分析解。本文用数值法研究了轨道偏心率较大的同步双星(EKCep)的轨道和自转演化的数值解和演化趋势。
1 从非自转同步演化方程组化为自转同步演化方程组
Zahn(1989)给出了由于潮汐摩擦使轨道半长轴a,轨道偏心率e和自转角速度的长期演化的一般方程组[4]:


式中,R和M分别表示主星的半径和质量;q=M’/M,M’为伴星质量;ω表示轨道角速度(平均运动);I表示转动惯量。对流摩擦时间tf和λIm已由Zahan&Bouchet(1989b)给出[5]:

式中,L和Te分别是主星的光度和表面有效温度;f⊙和T⊙e分别表示太阳的对流摩擦时间和表面有效温度。


根据Kepler第三定律也可写成以下联立方程组:

式中,T表示轨道周期(平均运动);P表示主星的自转周期。
轨道圆形化时间tair是[4]

对于同步双星λ=κ2(拱线进动常数)
2 长期演化方程组的数值解法
方程组(5)-(7)是三元联立常微分方程组。这类方程组可直接用积分方程组的分析解法;另外也可以用数值解法。前者可用指数级数展开得到分析解,但指数级数展开后只能对轨道偏心率小的项可以略去,对轨道偏心率较大的双星不能略去。本文所研究的同步双星EKCep的轨道偏心率较大(e =0.11),故不能用指数级数展开的分析法,只能用数值积分法。
数值积分常微分方程组最好采用四阶龙格—库塔解法。将前节方程组(5)-(7)写成适用于四阶龙格—库塔解法如下形式:

对于主序星或亚巨星,其半径R是不变的或R为常数。
龙格—库塔四阶解的形式是:
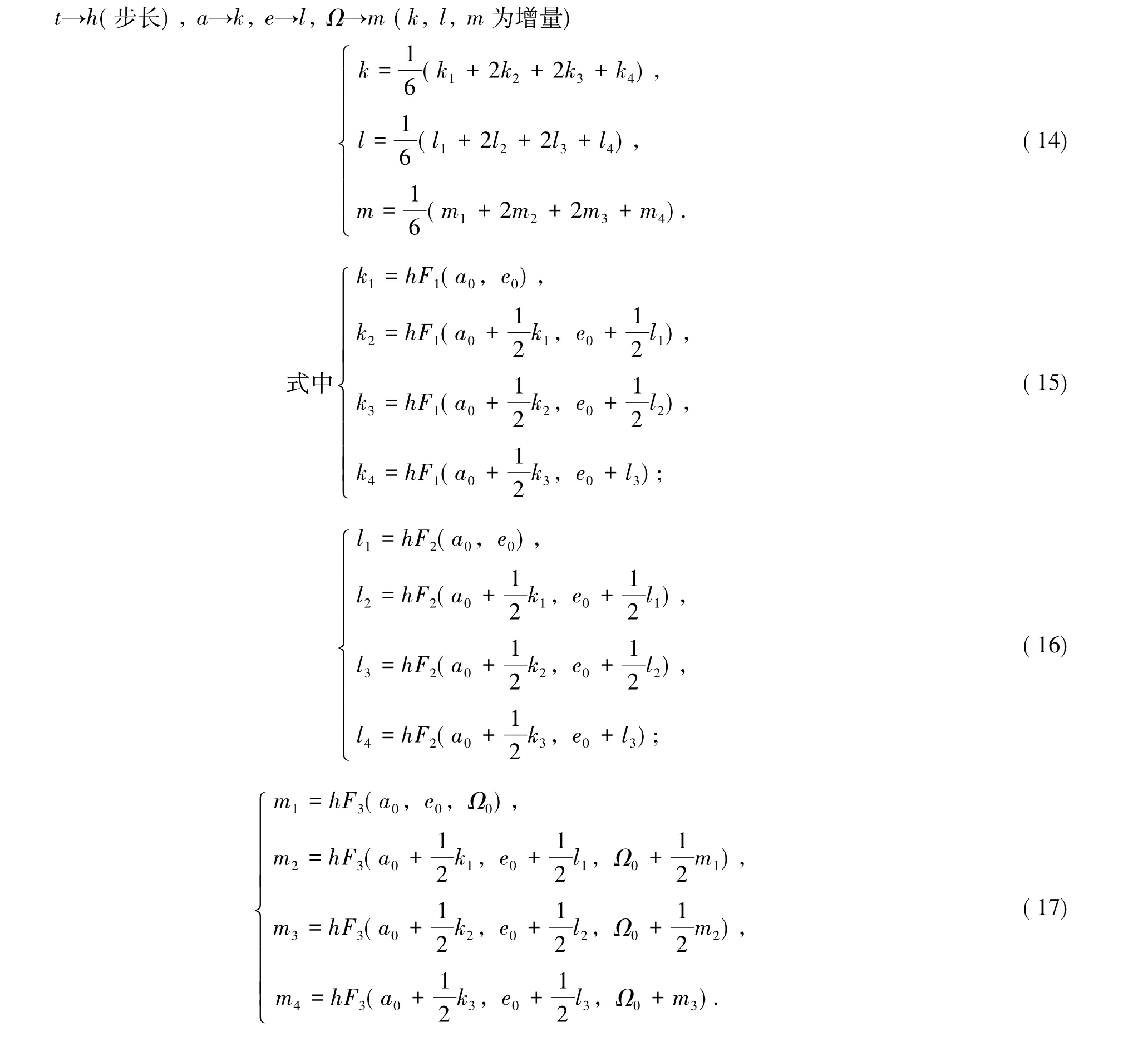
3 同步双星EKCep达到轨道同形化时的轨道和自转的演化数值解
本文利用前节的龙格—库塔计算方法计算同步双星EKCep达到轨道圆形化时轨道半长轴、轨道偏心率、轨道周期、轨道角速度和主星自转角速度的演化值。对于密近双星EKCep其系统属于DS(分离)系统。根据文[16]给出的光谱型,主星是AOV(AO型主序星),但根据文[6-7,17]主星是AOIV型(AO型亚巨星)。根据文[16]系统的同步性V=20 km/s,Vk=18 km/s。文[7]也给出Vsini=20 km/s,Vk= 18 km/s,所以判断此双星系是同步双星。此双星系的轨道参数:文[7-8,17]均给出的轨道偏心率e= 0.11。文[18]给出的轨道参数:T=4.427 8日,a=16.72R⊙,R=1.35R⊙,R’=1.14R⊙,q=M’/M=0.56,SM=M+M’=3.20M⊙,即M=2.05M⊙,M’=1.15M⊙,Te=103 200K(主星)。文[5]给出f⊙=0.433年,Te⊙=577 00K。根据上述V=20 km/s,R=1.35R⊙,Ω0=V/R=2.128 6×10-5rad/s,将这些数据代入(4)式,得潮汐摩擦时间:

对于同步双星λ=k2(拱线常数)。k2可用文[19]根据logm的数值在表中查找k2的对应值。但本文log2.05=0.317 7,表中没有k2的对应值。故只好用Cowlling公式计算k1=k2=k[20]
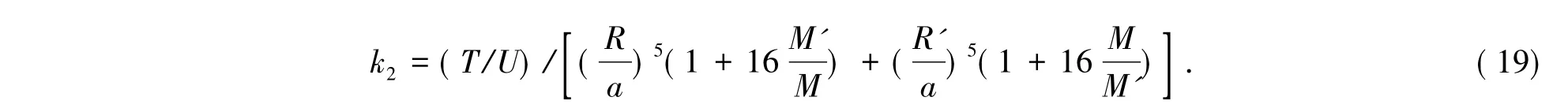
其中U是拱线进动周期,文[21]给出的数据,对于EKCep,U=4000年。将上述T、U、R、R’、M和M’代入上式后得:
k2=0.033 59.
再将λ=k2=0.033 59,tf=0.253 3年以及q=0.56,R=1.35R⊙,a=16.72R⊙代入(11)式后得轨道圆形化时间:t再将q,k,t,R,M和I代入(13)式中有:


在前节龙格—库塔公式(14)-(17)中利用初始条件值a0=16.7R0,e0=0.11,Ω0=V/R=2.128 6× 10-5rad/s以及A、B、C和h=ta.r=2.275 7×108年值,逐步得到
k1=-1.097R⊙,k2=-0.348 0R⊙,k3=-0.535 3R⊙,k4=-0.951 8R6,
l1=-0.109 97,l2=-0.071 9,l3=-0.081 1,l4=-0.035 7,
m1=2.430 7×10-5rad/s,m2=1.170 1×10-5rad/s,m3=1.464 2×10-5rad/s,m4=0.034 4×10-5rad/s.将这些数值代入(14)式得到轨道圆形化时轨道和自转的演变增量:
k=-0.636 0R⊙,l=-0.051 6,m=1.288 8×10-5rad/s.所以轨道达到圆形化时轨道半长轴、偏心率和主星自转角速度各值为:

即在2.275 7×108年内轨道和自转的变化值:
δa=-0.636 0R⊙,δe=-0.051 6,δΩ=+1.288 8×10-5rad/s.积分(8)-(10)式的结果给出:
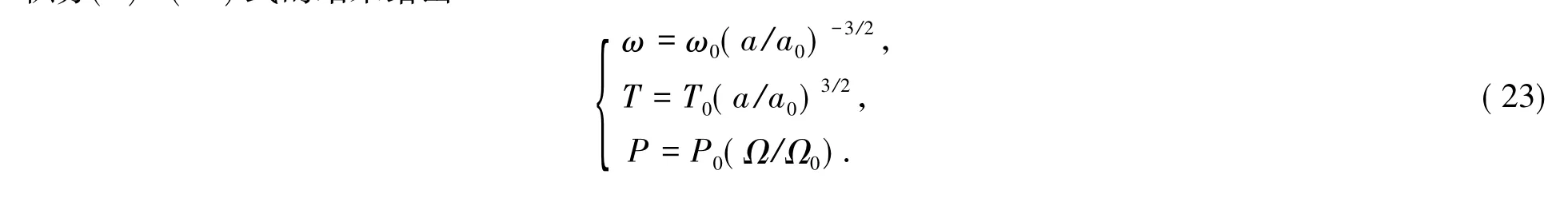
式中,T0=4.427 8日;ω=2π/T0=1.419 0 rad/日;P0=2π/Ω0=3.416 4日。
将a0=16.72R⊙,a=16.084R⊙,Ω0=2.128 8×10-5rad/s和Ω=3.417 4×10-5rad/s代入上式后得:
ω=1.503 8 rad/日,T=4.177 6日,P=2.127 7日,δω=+0.084 8 rad/日,δT=-0.250 2日,δP=-1.288 7日,δΩ=+1.288 6×10-5rad/s。
4 推论
根据前节的计算结果,可以推论同步双星EKCep两子星达到轨道圆形化时轨道和自转的演化趋势:
(1)轨道半长轴在近2×108年内从开始值16.72R⊙减少到16.084R⊙;
(2)轨道偏心率在近2×108年内从0.11减少到0.058 4;
(3)轨道角速度(平均运动)在近2×108年内从1.419 0 rad/日加速到1.503 8 rad/日;
(4)轨道周期在近2×108年内从4.427 8日缩短到4.177 6日;
(5)主星的自转角速度在近2×108年从开始值2.128 6×10-5rad/s加速到3.417 4×10-5rad/s;
(6)主星的自转周期在近2×108年内从开始值3.416 4日缩短到2.127 7日。
从同步演化方程组(5)-(10)还可推论轨道达到圆形化时间以后轨道半长轴和轨道偏心率也继续减少;轨道平均运动继续加速,轨道周期继续缩短,而主星自转角速度继续加速,周期继续缩短。
[1]P Hut.Stability of tidal equilibrium[J].Astronomy and Astrophysics,1980,92:167-170.
[2]P Hut.Tidal evolution in Close binary system[J].Astronomy and Astrophysics,1981,99:126-140.
[3]JP Zahn.Tidal friction in close binary stars[J].Astronomy and Astrophysics,1977,57:383-394.
[4]JP Zahn.Tidal evolution of close binary stars,I.Revisiting the theory of the equilibrium tide[J].Astronomy and Astrophysics,1989,220:112-116.
[5]JP Zahn,L Bouchet.Tidal evolution of close binary stars II.Orbital Circula-rization of late-type binaries[J].Astronomy and Astrophysics,1989,223(1):112-118.
[6]谭徽松.大陵五型双星的自转统计研究[J].天文学报,1989,30(2):135-148.Tan Huisong.Statistical study of the rotation of Algols[J].Acta Astronomical Sinica,1989,30(2):135-148.
[7]谭徽松,潘开科,汪洵浩.密近双星自转的测量和研究(II)自转同步性的计算[J].天体物理学报,1995,15(1):57-69.Tan Huisong,Pan Kaike,Wang Xunhao.Measurement and Study of Rotation in Close Binary Stars(Ⅱ)Synchronization Calculation[J].Acta Astrophysica Sinica,1995,15(1):57-69.
[8]潘开科.密近双星自转的测量和研究(III)同步性的统计性质 [J].天体物理学报,1996,16(3):291-297.Pan Kaike.Measurement and study of rotation in close binary stars(Ⅲ)statistical analysis of synchronization[J].Acta Astrophysica Sinica,1996,16(3):291-297.
[9]李林森.判断双星自转同步性的一种新方法 [J].天体物理学报,1998,18(1):77-82.Li Linsen.A new method for judging the synchronous rotation of binary stars[J].Acta Astrophysica Sinica,1998,18(1):77-82.
[10] 黄润乾,曽艺容.非同步转动双星系统的演化 [J].中国科学A辑,数学,2000,30(2): 187-192.
[11]Huang Runqian,Zeng Yiron.Evolution of Non-Synchronized Binary Systems[J].Science in China,Series A.Mathematics,2000,43(3):331-336.
[12]Li Linsen.An apparent descriptive method for judging the synchronization of rotation of binary stars[J].Journal of Astrophysics and Astronomy,2004,25(3-4):203-212.
[13] SMeibom,RDMathieu,K G Stassun.An observational study of tidal synchronization in Solar-binary stars in the open clusters M 35 and M34[J].The Astrophys Journal,2006,653(2):621-635.
[14] 李林森.判断分光双星自转同步性方法的理论改进[J].天文研究与技术——国家天文台台刊,2009,6(4):264-270.Li Linsen.Theoretical improvement ofmethods for judging the synchronization of self rotations of stars in a spectroscopic binary system [J].Astronomical Research & Technology——Publications of National Astronomical Observatories of China,2009,6(4):264-270.
[15]Li Linsen.Orbit and spin evolution of synchronous binary stars on the main sequence[J].Research in Astronomy and Astrophysics,2012,12(12):1673-1680.
[16]G Giuricin,FMardirossian,M Mezzetti.Synchronization in eclipsing binary stars[J].Astronomy and Astrophysics,1984,131(1):152-158.
[17] A H Batten,JM Fletcher,D GMaccarthy.Eight catalogue of the orbital elements of spectroscopic binary system[J].Publication of Dominion Astrophysics of Observatory,1989,17:1-127.
[18] H K Brancewiez,T Z Dworak.A catalogue of parameters for eclipsing binaries[J].Acta Astronomica,1980,30(4):501-524.
[19]A Claret,A Gimenez.Evolutionary stellarmodels using Rogers&Iglesias opacitieswith particalar attention to internal structure constants[J].Astronomy and Astrophysics Supplement Series,1992,96(1):255-261.
[20]T G Cowlling.On themotion of the apsidal line in close binary systems[J].Monthly Notices of the Royal Astronomical Society,1938,98(2):734-743.
[21]T Hegeds.AN up-dated List of eclipsing binaries showing apsidal motion[J].Bulletin d' Information du Centre de Donnees Stellaire,1988,35(1):15-28.
Numerical Solutions and Evolutionary Trends of the Orbit and Rotation of a Synchronous Binary-Star System at the Orbital Circularization Time
Li Linsen
(School of Physics,Northeast Normal University,Changchun 130024,China)
This paper derives a setof equations for the orbitand self-rotation of a synchronous binary-star system from the set of equations for non-synchronous binary stars.The numerical solutions of the equations as derived are subsequently given by using a numerical method.The circularization time,and the numerical values of the orbital semi-major axis,eccentricity,and the rotational angular velocity together with other parameters at that time are calculated for the synchronous binary-star system EKCep.The paper finallymakes certain colollaries about the evolutionary trends of the orbit and self-rotation of the system.
Synchronous binary stars EKCep;Orbital circularization time;Orbit and rotation;Numerical solution
P144;P153
:A
:1672-7673(2013)03-0249-06
2012-08-26;修定日期:2012-09-14
李林森,男,教授.研究方向:天体轨道参数变化和天体自转理论.Email:dbsd-lls@163.com
CN 53-1189/P ISSN 1672-7673

