阵列接收系统的噪声温度分析*

段 焱，王 壮，程 翥

（1.国防科技大学电子科学与工程学院ATR实验室，湖南长沙 410073；2.国防科技大学电子科学与工程学院电子工程所，湖南长沙 410073）

阵列接收系统的噪声温度分析*

段 焱1，王 壮1，程 翥2

（1.国防科技大学电子科学与工程学院ATR实验室，湖南长沙 410073；2.国防科技大学电子科学与工程学院电子工程所，湖南长沙 410073）

针对射电天文抗干扰技术对于射电天文观测设备灵敏度的影响，分析了评估自适应波束形成技术对阵列接收系统的噪声温度影响。首先通过噪声信号模型，获取了影响系统噪声温度变化的参数，并在此基础上研究了天线增益、接收机增益和耦合性等系统参数的不确定性对于噪声温度的影响，最后利用仿真实验分析了理想系统条件下当前主要的自适应波束形成算法对于系统噪声温度的影响。结果表明基于自适应波束形成的抗干扰方法在天文信号源和干扰信号源重合的情况下已不再适用。

射电天文；信号处理；自适应波束形成；噪声温度

在射电天文领域中，抗干扰处理不仅要抑制干扰，更要考虑抗干扰方案对于天文应用的影响。由于天文信号在大部分情况下可以看成噪声功率的微小增加，需要很长的积累才能从噪声中显现，这使得在设计射电天文抗干扰方法时，不仅需要考虑干扰的抑制，还要保证系统噪声温度的可控性和可预知性。因此，系统噪声温度的起伏不仅决定了射电天文观测工具对天文信号的最小可检测级别［1］，也是衡量射电天文抗干扰技术性能的重要指标之一。

对于新一代采用了相控阵接收体制的射电天文望远镜［2］，由于多通道接收的特点，传统的基于单通道接收机的噪声温度标准差公式已不适用基于阵列接收系统的射电天文望远镜。针对上述问题，文［3］作者通过建立和分析阵列接收系统的散射矩阵模型，得到了阵列接收系统输出的等效系统噪声温度和波束形成器权值间的参数关系，并基于上述关系推导和分析了阵列接收系统的波束灵敏度公式；文［4］作者通过阵列接收系统的阻抗矩阵模型得到了相同的结论，而且证明了这两种分析方法是等价的［5］。目前，基于波束形成的空域滤波不仅在雷达、通信、声纳等领域广泛应用［6］，同时针对相控阵接收体制的射电天文望远镜的这类抗干扰方法也已经在射电天文领域取得了应用［7-8］。这种方法的应用使得接收机的增益不仅是一个随机变量，也由于权值的更新有了时变的特性，进而使得阵列接收系统的噪声温度和噪声温度标准差有了时变特性。因此，获得自适应波束形成器的权值与系统噪声温度之间的参数是必要的。并且在此基础上，可以从对噪声影响的角度，分析现有的自适应波束形成的抗干扰算法被验证是否适用于射电天文抗干扰技术中。

基于文献［3-5］的研究成果，本文建立了相控阵体制射电天文望远镜的噪声信号模型，并分析了系统参数不确定性和系统间耦合对系统噪声参数的影响。在此基础上，通过仿真实验验证了理想系统条件下基于自适应波束形成的抗干扰处理对于系统噪声温度的影响。

1 噪声信号模型

对于基于阵列接收系统的射电接收机而言，其接收机结构如图1［9］。对于接收机前端，其具体组成如图2［1，10］。

图1 基于阵列接收系统的射电接收机示意图Fig.1 Structureofthereceiverfortheantennaarray

图2 接收机前端组成示意图Fig.2 Structureofthefrontendofthereceiver

一般来说，接收机前端由低噪声放大器（LNA）、混频器、中频放大器（IF）、带通滤波器等组成。假设阵列接收系统有M个阵元，接收的信号为窄带信号，接收机前端的处理带宽为B，增益grec为M ×M大小的矩阵。令波束形成器的权值为一个M×1维的复矢量W，

从系统外部进入的噪声信号n1的分量独立同分布，在第n个时刻n1为一个M×1维的列矢量［2］：

这里，n1［n］的各个分量为互不相关的高斯白噪声。其中，nsp［n］表示从天线旁瓣进入的地面辐射噪声，也称溢出噪声；nbg［n］和natm［n］分别表示天空背景噪声和大气微波辐射噪声。那么n1［n］的每个分量的方差为［10］：

式中，T1表示n1［n］各个分量的等效噪声温度；Δf为天线接收的频率范围；kb为波尔兹曼常数；ηrad表示阵列天线的接收效率，它是一个与天线散射矩阵、接收机前端增益、波束形成器权值矢量有关的值［3，11］，即：

对于从外部进入系统的噪声信号，其等效噪声温度T1可以表示为一个与天线方向图和功率增益的函数［12］：

式中，Ga（θ，φ）表示天线的功率方向图；p（θ，φ）表示外来噪声功率密度（W/Hz/steradian）的空间分布。从（4）、（5）式可以看出，n1功率的大小受到了天线接收效率、功率方向图的影响，他们均与波束形成器的权值有关。因此对于采用了自适应波束形成技术的阵列系统，其接收效率不再是一个恒定值。天线的功率增益方向图对噪声温度的影响的分析将在第三部分中给出。

n1［n］经过接收机前端和波束形成器后，波束形成器输出的噪声n2［n］为：

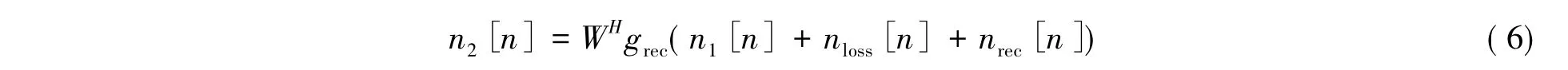
其中nrec［n］为接收机前端产生的，各个支路间相互独立的噪声信号。nloss［n］表示天线热损耗产生的噪声信号，两者都可以认为是高斯白噪声。对于nloss［n］，假设每一路的热损耗噪声独立同分布，nloss［n］的第m个支路的噪声功率为：

式中，T0表示环境温度。从上述过程中可以看到，整个处理过程是一个线性的处理过程，因此最终的输出n2［n］也是一个高斯白噪声，其功率为：

其中Rn1、Rnloss、Rnrec分别为n1［n］、nloss［n］、nrec［n］的自相关矩阵，由于不同来源的噪声、不同的支路的噪声均是独立不相关的，因此可以写为：

I表示单位矩阵，σ2recm表示接收机前端在第m个支路产生的噪声信号的功率，

Trecm表示在该支路中，接收机前端产生的噪声信号的等效噪声温度。利用（9）式，Rnrec可以表示为：

将（8）式、（9）式代入（7）式中，σ2

n2可以表示为：

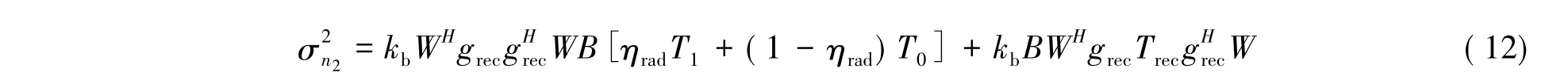
从（5）、（13）式可知，影响噪声功率变化的主要因素有3个：权值的变化、接收机前端增益的不确定性、天线功率增益的不确定性。

2 系统参数的不确定性对于噪声温度的影响

由于长时间使用、设备老化等问题，接收系统的增益会缓慢地发生变化，而不再是一个恒定值，这个变化过程会直接影响噪声温度的起伏，因此定期的测量接收系统的增益是必要的，这也是标校工作的重要组成部分［13］。测量值与实际值之间往往会有一定的误差，而这个误差对于噪声温度的影响是必须论证的。

理想情况下，grec是一个对角阵，同时各个支路的增益相等，即：

其中g表示各个支路的增益。进一步，如果nrec［n］的各个分量同分布，且等效噪声温度为Trec，那么，对于（13）式可以改写为：

g2为接收机前端的功率增益。令G=g2，ΔG为功率增益的不确定度，提取常数项kbB，因为增益起伏而导致的噪声温度变化为ΔGWHW（ηradT1+（1-ηrad）T0+Trec）/G。类似地，根据（5）式，由于天线功率方向图的不确定性导致的噪声温度变化为：

其中，ΔGa（θ，φ）表示天线增益方向图的不确定度。根据（14）、（15）式，由于天线功率方向图和接收机前端功率增益的不确定性导致的系统噪声温度变化ΔTsys为：

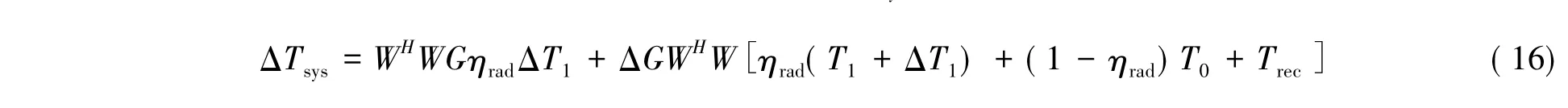
不同的射电辐射接收机性能参数也是不一样的。同时，由于设备运行情况的差异和校准工作的精确程度不同，天线功率方向图和接收机前端功率增益的不确定性也是不同的。所以，没有一个统一的评价标准来判断天线功率方向图和接收机前端功率增益对噪声温度变化的影响小到什么程度可以被忽略。

一般来说，与ΔTsvs相比，在输出端的天文信号的等效温度Ts可能在同一个数量级，甚至低于ΔTsvs若干个数量级。因此，类似于超噪比（Excess Noise Radio，ENR）［14］，可以用在系统输出端的Ts和ΔTsvs的比值SNRΔ衡量对天文观测的影响。假设天文信号经过天σ线后的等效温度为Tb，SNRΔ可以写为：

而ΔTsys能否被忽略，取决于天文观测对SNRΔ的要求。

实际情况中，由于系统设计、设备运行等原因，阵列间的相互耦合的因素必须被考虑。那么grec和Trec对角线上的元素可能相等，但不再是一个对角矩阵［15］，因此理想系统条件下对于噪声温度的分析方式不再适用。从（13）式可以看出，对于从外部进入的噪声而言，从天线输出端到接收机输出端之间的增益G为。同时，假设Trec的对角线元素依然相等，均为Trec。将Trec进行划分，

那么对于式（13），可以重新写为：

可以看到，支路间的耦合性越强，即Trec-coup的各个元素值越大，系统输出的噪声功率也就越大，会导致信噪比的降低。

3 自适应波束形成算法对系统噪声温度的影响

根据（14）、（16）式，可以看到，理想系统条件下，自适应波束形成算法导致噪声温度变化的主要原因是由于权值模的平方和WHW随着自适应更新的过程可能发生变化；而当系统耦合必须被考虑时，自适应波束形成算法的影响主要体现在向量WHgrec中各个元素可能会发生变化。综上所述，如果实际系统在满足射电天文观测要求的前提下，要想尽可能减小自适应波束形成抗干扰方法对噪声温度的影响，系统近似为理想系统时，只需要保证WHW变化尽可能小，系统不能近似为理想系统时，就需要保证WHgrec中各个元素尽量保持不变。

在自适应波束形成算法中，最为常用的方法有线性约束最小方差法（Linear-Constraint Minimum Variance，LCMV）、最大信噪比法（Max SNR）、子空间投影法（Subspace Projection，SP）等方法［16］。为了讨论上述自适应波束形成方法对于系统噪声温度的影响，首先分析接收信号模型。假设如图2所示的阵列接收系统有M个阵列因子，并且接收了Q个不同的干扰信号，在第n个时刻，阵列接收系统所接收的输入信号Xin［n］为：

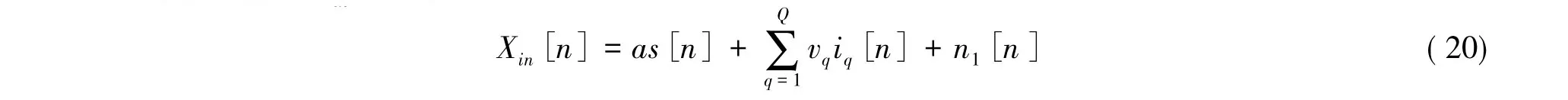
式中，s［n］为期望获得的信号；iq［n］为接收到的第q个干扰信号；n1［n］为噪声信号；a和vq分别表示天文信号与第q个干扰信号的阵列响应向量，维数为M。经过接收机前端和波束形成器后，输出信号可以表示为：

式中，s'［n］和i'q［n］分别表示经过混频、带通滤波和中频放大后的天文信号与第q个干扰信号。从（21）式可以看到，波束形成算法的目的就是在保证WHa基本不变的情况下使得WH∑Qq=1vqi'q［n］尽量小。因此，对于线性约束最小方差法而言，其最约束条件和最优权值Wopt形成条件为：

式中，Rx表示Xin［n］的协方差矩阵；C表示约束矩阵；f表示约束解：

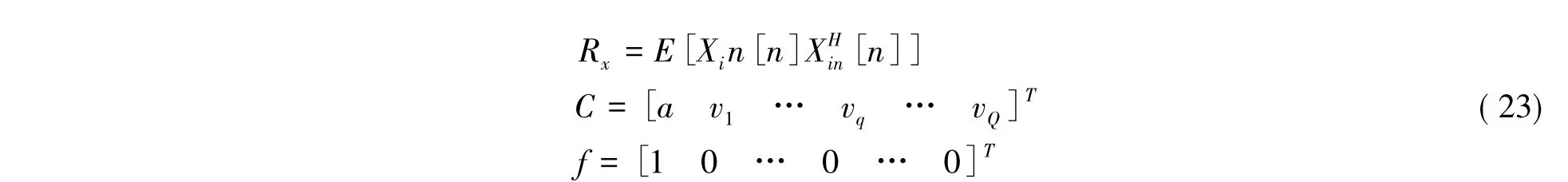
对于最大信噪比法而言，最优权值形成条件为：

式中，Rs表示天文信号的协方差矩阵；Ri+n表示干扰信号与噪声信号之和的协方差矩阵；λmax表示最大特征值。而子空间投影法求解Wopt的过程可以表示为：

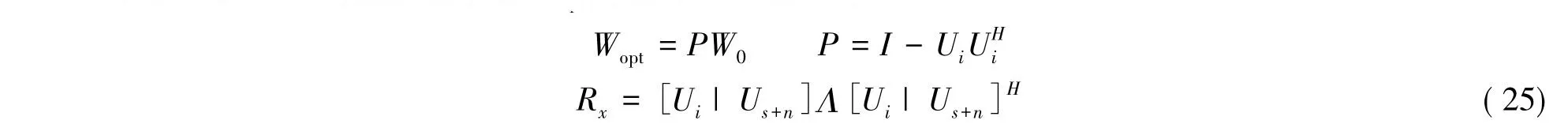
式中，Ud表示Rx最大的Q个特征值对应的特征向量。W0能使主瓣始终对准天文信号方向，这里W0

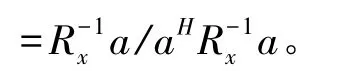
为了验证上述3种常用方法对于理想系统的噪声温度的影响，下面通过MATLAB仿真对上述算法在自适应更新的过程中wp=WHW的变化情况。

假设阵元数M为8，并且为均匀线阵，期望信号波达角方向为0°，干扰信号为中心频率在L1波段，即fL1=1 575.42MHz的C/A码GPS信号，干扰源数量为1。阵元间距d为c/2fL1。输入的噪声信号均为高斯白噪声，经过混频以后，中频的中心频率为10MHz。采样率25MHz，每次波束形成过程采样1ms，即样本长度N为25 000然后通过蒙特卡洛仿真（1 000次）观察wp的均值和方差的变化。

仿真实验一，假设干扰源固定，信噪比（SNR）为-20 dB，干扰信号波达角方向为60°，干扰信号与噪声比（Interference to Noise Ratio，INR）变化范围为-20 dB～20 dB，仿真结果图3。

图3的结果表明，当干扰源固定时，虽然INR在变化，但是3种方法wp的方差均很小，这说明当干扰源位置固定时，3种方法在抑制干扰的同时对噪声功率影响是可控的；从图4中可以看出，随着INR的变化，3种算法的波束形成方向图基本只是在60°变化相对较大。这表明权值的分量基本保持不变，与图4的仿真结果基本吻合。

仿真实验二，假设干扰源从-90°方向以0.5°的步长移动到90°，SNR为-20 dB，INR为0 dB，其它条件与仿真实验一相同。仿真结果如图5。

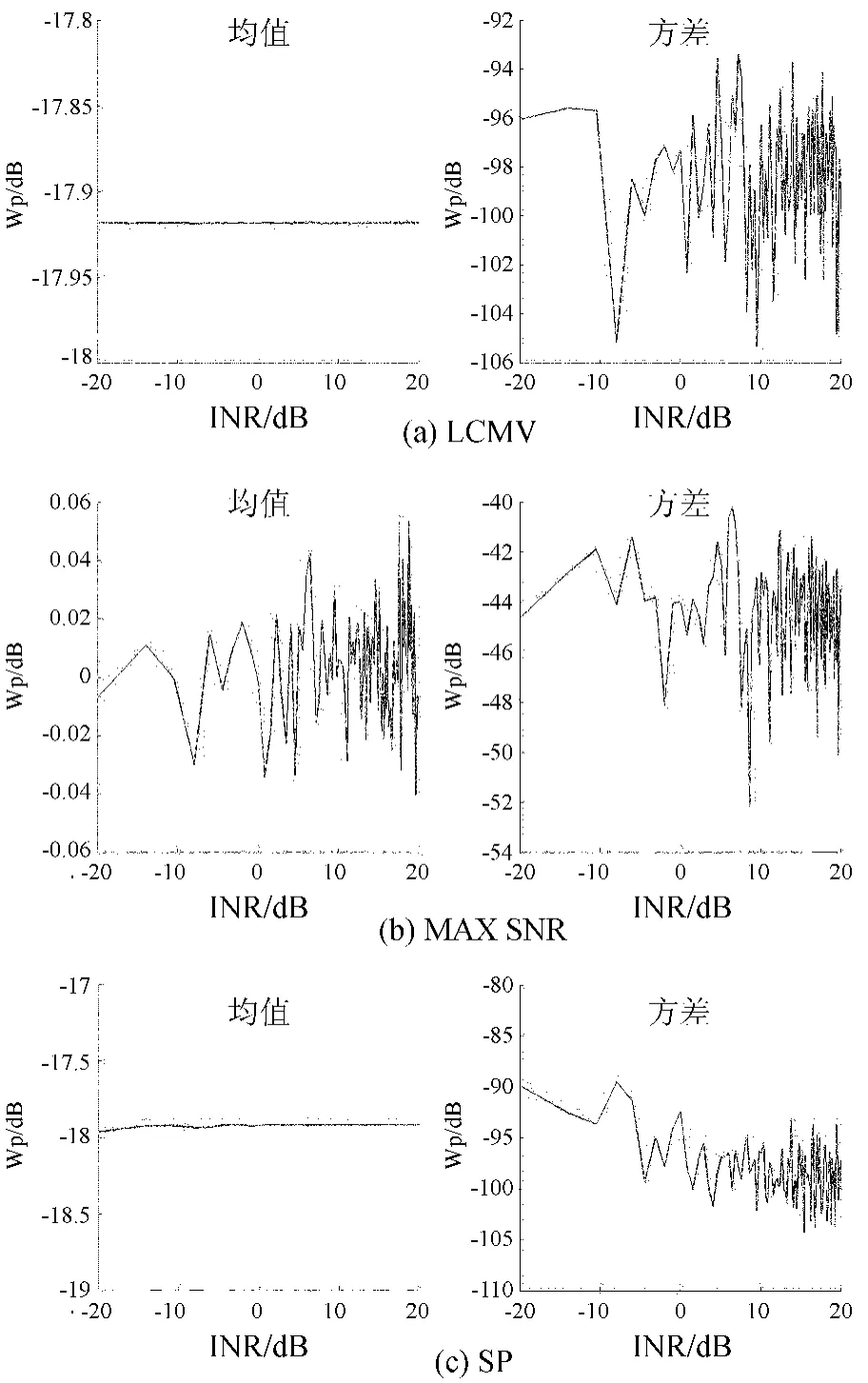
图3 仿真实验一结果Fig.3 Results of the Simulation Experiment 1

图4 实验一条件下波束方向图变化示意图Fig.4 Results of beam map under the condition of the Simulation Experiment 1

图5 仿真实验二结果Fig.5 Results of the Simulation Experiment 2

从图5可以看出，当干扰源移动的时候，3种方法中，Max SNR法依然始终为1，这是因为Max SNR形成的最优权值是单位化的特征向量，因此wp基本不变。但是根据（25）式，由于实际系统中很难实现天文信号和干扰信号与噪声信号的时域分离，因此在实际系统中的适用性不如LCMV法和SP法；LCMV法和SP法在干扰信号波达角和天文信号波达角重合的时候，wp的均值和方差都出现了起伏，这是因为根据（24）式，LCMV法的求解条件使得在干扰信号和天文信号波达角完全重合的时候无法得到最优解。对于SP法而言，干扰信号子空间Ui在干扰信号和天文信号波达角完全重合的时候与天文信号的阵列响应不再正交，从而导致了起伏。考虑到GPS、GLONASS、北斗等导航系统有多颗卫星组成，那么在一定的观测时间内，将不止一次出现天文信号波达角和干扰信号波达角重合的情况，因此不能直接用数据消除法处理这种情况，而是需要结合其它抗干扰方法来处理干扰信号。

4 结论

本文算法利用阵列接收系统的噪声信号模型，分析系统增益、天线增益、波束形成器权值的不确定性对于系统噪声温度的影响。利用仿真实验，讨论了当前主要的自适应波束形成算法在理想系统条件下对系统噪声温度的影响，结果表明基于自适应波束形成的抗干扰处理并不能适用于任意空域范围、任意时间段的干扰信号，需要结合其它类型的抗干扰处理方法抑制干扰。本文对于自适应波束形成算法可行性的验证是建立理想系统的条件之下，对结合实际系统条件下验证抗干扰算法的抗干扰性能以及抗干扰处理对系统噪声特性的影响有待进一步研究。

［1］Kristen Rohlfs，Thomas LWilson.Tools of radio astronomy［M］.Signal Processing and Receivers： Theory，2009.

［2］吴盛殷，甘恒谦，张海燕.孔径阵列技术及其在射电天文中的应用［J］.天文学进展，2008（3）：203-213.Wu Shengyin，Gan Hengqian，Zhang Haiyan.The AAT technique and its applications in radio astronomy［J］.Progress in Astronomy，2008（3）：203-213.

［3］Marianna V Ivashina，Rob Maaskant，Bert Woestenburg.Equivalent system representation to model the beam sensitivity of receiving antenna arrays［J］.IEEE Antenna and Wireless Propagation Letters，2008（7）：733-737.

［4］Karl FWarnick，Brian D Jeffs.Efficiencies and system temperature for a beamforming array［J］.IEEE Antenna and Wireless Propagation Letters，2008（7）：565-568.

［5］Karl F Warnick，Marianna V Ivashina，Rob Maaskant.Unifed defnitions of effciencies and system noise temperature for receiving antenna arrays［J］.IEEE Antenna and Wireless Propagation Letters，2010，6（58）：2121-2125.

［6］Van Veen B D，Buckley K M.Beamforming：a versatile approach to spatial filtering［J］.IEEE ASSP Magazine，1988，5（2）：4-24.

［7］Jamil Raza，Albert-Jan Boonstra，Alle-Jan van der Veen.Spatial filtering of RF interference in radio astronomy［J］.IEEE Signal Processing Letters，2002，2（9）：64-67.

［8］Jonathan Landon，Brian D Jeffs.Model-based subspace projection beamforming for deep interference nulling［J］.IEEE Transactions on Signal Processing，2012，3（60）：1215-1228.

［9］Brian D Jeffs.Signal processing for phased array feeds in radio astronomical telescopes［J］.IEEE Journal of Selected Topics in Signal Process，2008，5（2）：635-646.

［10］ 陈勇，孙正文，杨颖.S波段双极化低噪声接收机的设计与制作［J］.天文研究与技术——国家天文台台刊，2009，6（1）：57-62.Chen Yong，Sun Zhengwen，Yang Ying.Design and manufacture of a low-noise S-band dualpolarization receiver［J］.Astronomical Research＆ Technology——Publications of National Astronomical Observatories of China，2009，6（1）：57-62.

［11］ 王新稳，李萍，李延平.微波技术与天线［M］.北京：电子工业出版社，2006.

［12］ E E M Woestenburg.Defnition of array receiver gain and noise temperature［J/OL］.［2013-03 -19］.http：//www.skatelescope.org.

［13］Sebastiaan van der Tol，Brian D Jeffs，Alle-Jan van der Veen.Self-clibration for the LOFAR rdio atronomical aray［J］.IEEE Transaction on Signal Processing，2007，9（55）：4497-4510.

［14］ 陈勇，孙正文，袁建平，等.应用于射电天文的低噪声温度测量方法［J］.天文研究与技术——国家天文台台刊，2012，9（2）：129-136.Chen Yong，Sun Zhengwen，Yuan Jianping，et al.Low-noise temperaturemeasurementmethods in the radio astronomy［J］.Astronomical Research＆Technology——Publications of National Astronomical Observatories of China，2012，9（2）：129-136.

［15］Jonathan Landon.Phased aray fed clibration，bamforming，and iaging［J］.The Astronomical Journal，2010，139（3）：1154-1167.

［16］ 张小飞，汪飞，徐大专.阵列信号处理的理论与应用［M］.北京：国防工业出版社，2010.

Analysis of the Noise Tem perature of an Antenna Array Receiver

Duan Yan1，Wang Zhuang1，Cheng Zhu2
（1.ATR Key Lab，School of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China，Email：duanyan13@sina.cn；2.Research Institution of Electronic Engineering，School of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China）

For evaluating effects of the interference mitigation technology on the sensitivity of an astronomical radio device，we propose a method to estimate the influence of the adaptive beam-forming technique on the noise temperature of an antenna array receiver system.Using a correct noisemodelwe derive the relation between noise temperature and system parameters.We subsequently use the relation to analyze how the uncertainties of some system parameters（e.g.，antenna gain，receiver gain，and system coupling）are affected by the noise temperature.We use simulations to test the influence of the currentmain adaptive beamforming algorithm on the noise temperature.The results indicate that the interference mitigation processing based on the adaptive beam-forming technique is insufficient in cases that astronomical signals and interference signals severely overlap.It appears necessary to solve this problem by combining other interferencemitigation methods in the temporal or frequency domain with the adaptive beam-forming technique.Our analysis results need to be further verified for real situations.

Radio astronomy；Signal processing；Adaptive beam-forming；Noise temperature

TN973

：A

：1672-7673（2013）03-0234-08

国家自然科学基金（11173068）资助.

2013-03-19；修定日期：2013-04-20

段 焱，男，硕士.研究方向：信号处理.Email：duanyan13@sina.cn

CN 53-1189/P ISSN 1672-7673