低压动态补偿装置的检测与控制优化

文 芸，肖 凡，姚 鹏，范瑞祥，徐在德

（1.江西南昌供电公司，江西南昌 330006；2.湖南大学电气与信息工程学院，湖南 长沙 410082；3.江西省电力科学研究院，江西南昌 330096）

0 引言

随着大功率晶体管、功率场效应管及绝缘栅型双极性晶体管等新型快速大容量功率开关器件的出现，结合瞬时谐波电流检测方法的提出，先进的控制理论和PWM调制技术的快速发展以及高速、高性能微处理器和数字信号处理器等的出现，使得有源滤波技术得到快速的发展。有源电力滤波器在电网低压侧针对谐波抑制和无功补偿得到大量实践利用。

现运行的低压动态补偿装置以并联型有源电力滤波器为主，其主要针对系统负载侧谐波电流进行补偿，具有一定的无功补偿能力。传统的并联型有源电力滤波器检测环节主要以基于瞬时无功功率理论的p-q算法和ip-iq算法为主，进行谐波的全检测。这样的检测方式不具有针对性，不能合理的分配有源滤波器的容量问题，存在容量浪费现象。特别是在装有无源滤波装置的负载侧可能会导致有源滤波器发出的谐波电流大量流入无源补偿装置，导致无源补偿装置的过流等现象。

有源电力滤波器普遍采取电流电压双闭环PI控制，但PI参数整定后一般就不再变化，针对实时动态变化的负荷，则补偿精度存在不足。本文在分析了传统PI控制的基础上，提出模糊PI控制器，适时的改变P，I参数，满足系统响应迅速，且具有满意的控制精度。

1 低压动态补偿装置的原理分析及检测优化

1.1 并联型有源电力滤波器的结构

并联型有源电力滤波器的主电路为PWM变流器，现今主要使用的为电压源型结构。系统检测电网负载侧三相电流，通过分频检测计算出某一次或某几次谐波电流值，同时加入直流侧稳压控制电流得到指令电流ic；再引入逆变器输出电流作为反馈做差得指令电流△ic；最后由模糊PI控制器输出PWM信号，完成对变流器的操作。

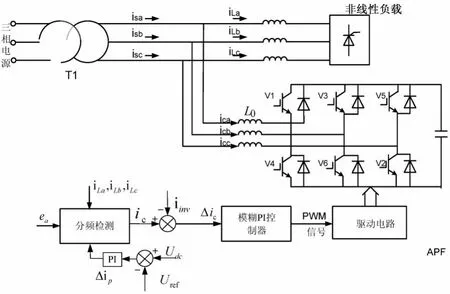
图1 并联型有源电力滤波器拓扑及系统构成

1.2 传统的ip-iq检测方法

谐波电流的检测关系到实际补偿效果的好坏，能够准确快速的检测系统中的谐波电流，是完成补偿要求的基础。传统的谐波电流检测和无功电流检测主要以ip-iq算法为主，能够检测出负载侧的所有谐波电流，且有较好的实时性。但缺点是不能体现出系统中某一次或者某几次谐波电流的大小和含量，不能有针对性的进行谐波补偿，使得有源电力滤波器的容量得不到较好的分配。

传统的ip-iq算法以瞬时无功功率理论为基础，通过坐标变换将检测的三相电流转换成两相电流值ip，iq，通过低通滤波器得到基波的直流分量，最后经反坐标变换得到检测电流的基波分量。其运算原理图如下：

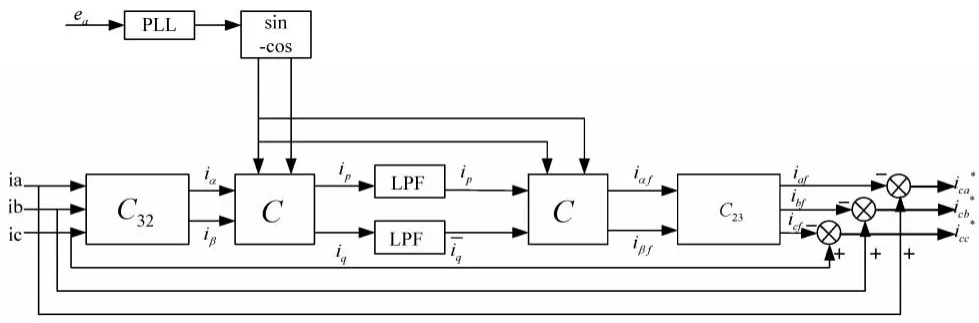
图1 ip-iq算法原理图

ea为系统电源侧a相的电值；为基波分量；PLL为锁相环；LPF为低通滤波器，C32,C分别为：

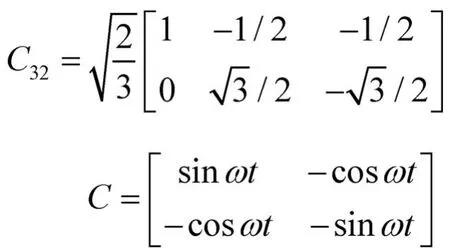
假设被检测三相电流对称，分别为：

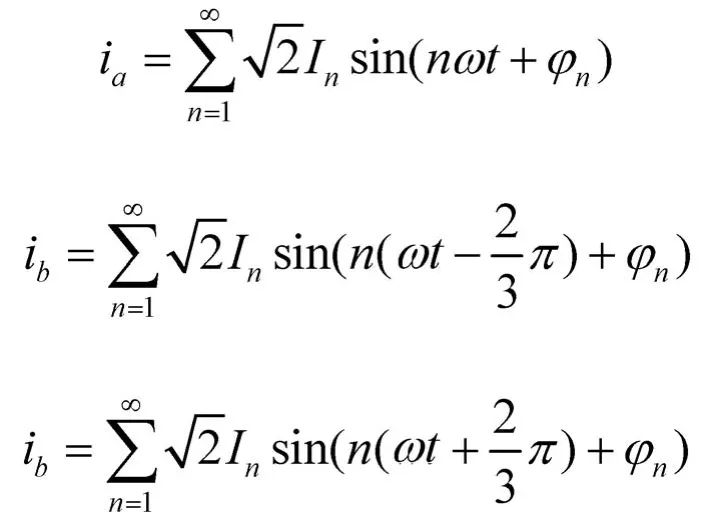
式中：n=3k±1，k为整数（k=0时，只取＋号，即只取n＝1）。

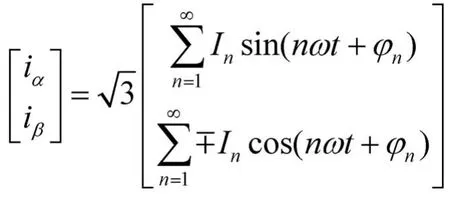
式中n=3k+1时取上符号，n=3k-1时取下符号。

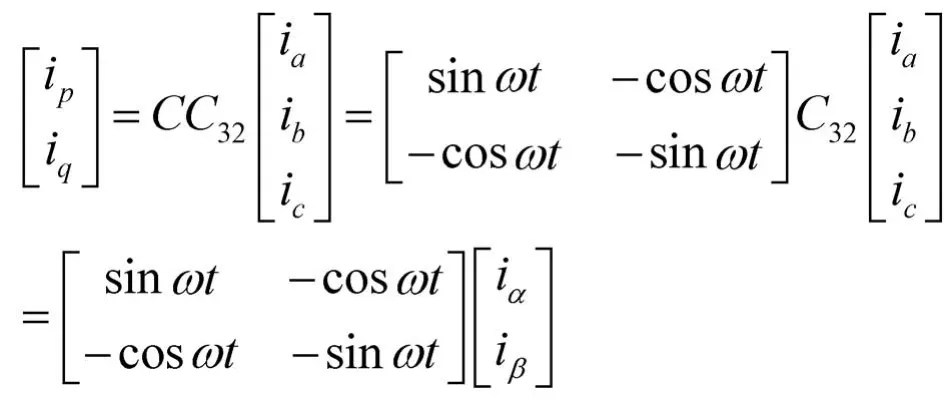
1.3 改进型的ip-iq算法原理

从对传统ip-iq算法算法的分析可以看出，其计算出三相电流的基波正序电流值后与三相电流做差得到系统的谐波电流值和无功分量。这里的谐波电流包含了系统几乎所有的谐波电流，含量比较复杂。而在实际的低压补偿装置安装处，负载的谐波电流往往以一次，或者几次居多，而其它较高次谐波则含量很少，针对实际的补偿情况，检测出主要的谐波成分，进行满足电网谐波要求的有针对性的谐波补偿，可以节省并联型有源滤波器容量，使其可以在允许范围内考虑负荷无功缺失，进行一定量的无功补偿，能实现对电能质量的优化控制。

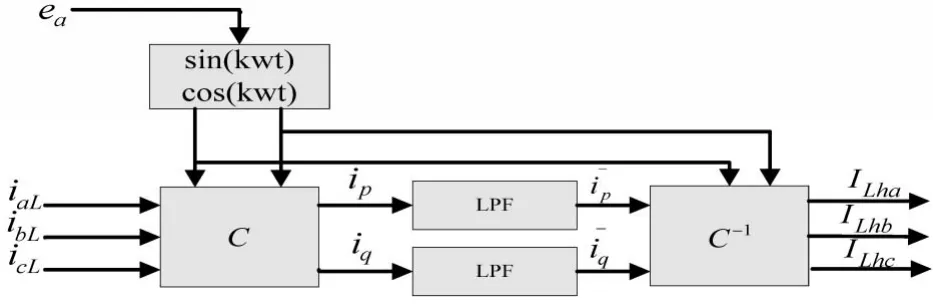
图2 改进型ip-iq算法原理图

针对文献[4]提出的任意次谐波电流检测方法，进行简化得到了这种改进型的ip-iq算法。如图2所示，基于瞬时无功功率的ip-iq算法，检测的电网电流经过变换矩阵C，低通滤波后得到k次谐波的有功和无功的直流分量，再反变换得到k次谐波分量。根据上述原则，若欲检测某次（如k次）谐波电流分量，参考电压矢量选为k次谐波电压矢量即可，

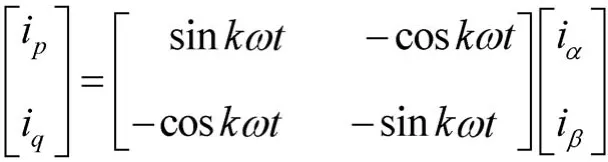
此时的ip-iq变换及其逆变为

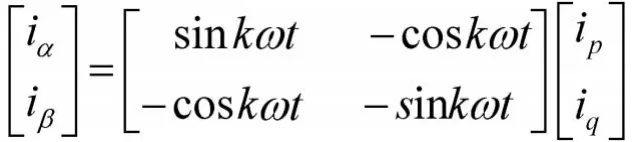
其逆变换为

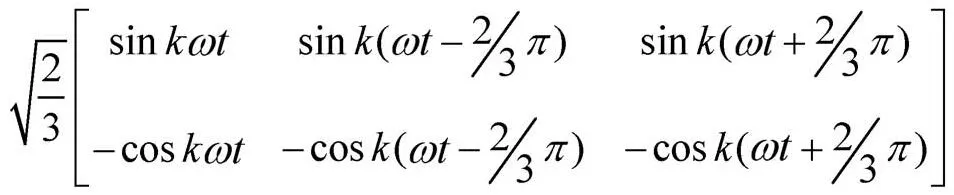
图中矩阵C为

当k=1时，检测结果即为基波正序电流分量。k取不同的值即可检测不同次数谐波分量，实现分频检测的改进ip-iq算法。

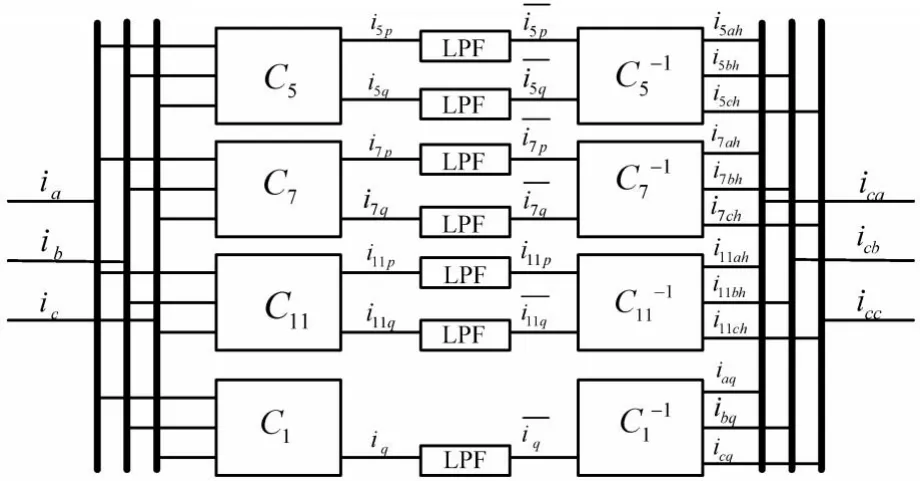
图3 基于改进型ip-iq算法的并行检测框图

随着DSP等高速数字处理芯片的适用，使得分频检测的实现变得更为简单，图3给出了基于改进型ip-iq算法的并行检测框图。可以针对具体情况有选择性的增加或者减少需要检测的谐波分量，其中：

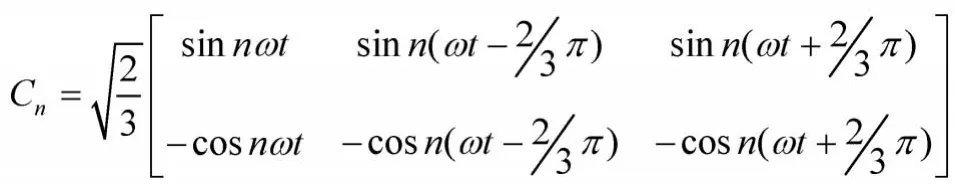
与图2中的C相似，n=1时表示以基波频率为基准的变换，在分频检测中，主要用于计算需要补偿的无功电流。

2 模糊PI控制器的实现

有源电力滤波器主要以PI控制为主，PI控制结构简单易于实现，参数容易整定，且控制精度较好。但考虑系统中负荷特性的不断变化，以及系统运行方式的改变，传统PI的不足也逐渐体现，主要为控制精度的缺陷，因此提出模糊PI控制方式，通过实时动态改变PI参数，能更好好的跟踪系统的变化，更好的补偿谐波，达到高精度的目的。

2.1 传统PI控制

常规PI控制器的作用，可描述为：

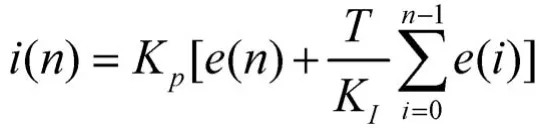
式中：e（n）为第个采样时刻控制器的输入量(偏差量)；i（n），i（n-1）为第个和第个采样时刻控制器的输出量(控制量)；T为采样周期；KI为积分时间常数；KP为比例增益。

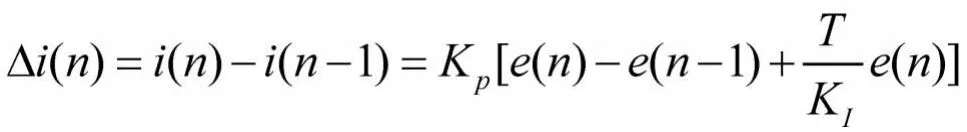
由上式可得，控制器的i（n）和i（n-1）之间的增量为：KI，KP参数的整定多以Ziegler-Nichols为主，先置KI=KP=0，再增加KP，直至系统振荡，记下该临界状态的KP值为Kcr，振荡周期为Tcr。此时，可确定控制器参数为：KP=0.45Kcr，KI=0.85Kcr。

2.2 模糊PI控制器的设计：

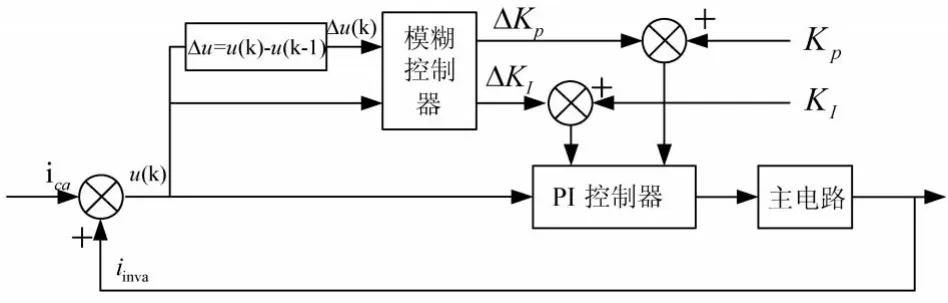
图4 模糊PI控制结构图

以A相位例，图中ica为A相指令电流，iinva为A相逆变器输出电流，KP为初始整定的P值，KI为初始整定的I值。△Kp为模糊控制器输出的P值的改变值，△KI为模糊控制器输出的I值的改变值。

将模糊控制器的输入变量u（k）和△u（k）均分为7个语言值。即：{NB，NM，NS，O，PS，PM，PB}，隶属度函数采用灵敏性强的三角函数。

△Kp的模糊规则为：

1）如果u（k）的值为NB,△u（k）的值为NB，则△Kp值为PB；

2）如果u（k）的值为PB,△u（k）的值为PB，则△Kp值为NB；

3）如果u（k）的值为NB,△u（k）的值为NS，则△Kp值为PM；

4）如果u（k）的值为NS，△u（k）的值为NS，则△Kp值为NS；

5）如果u（k）的值为0，△u（k）的值为0，则△Kp值为0；

6）如果u（k）的值为PS，△u（k）的值为PS，则△Kp值为NS；

7）如果u（k）的值为PB，△u（k）的值为PS，则△Kp值为NM。

比例环节主要为了快速响应，因此当u（k）值过大或者过小，为提高响应速度△Kp的值取反向的最大值。当u（k）值较小时，不宜过大，因为△Kp过大容易引起超调过大而导致系统振荡，要合理取值。同时考虑 的作用，当u（k）和△u（k）同号时△Kp取小值，反之取大值。

△Kp的模糊规则为：

1）如果u（k）的值为NB,△u（k）的值为NB，则△KI值为0；

2）如果u（k）的值为PB,△u（k）的值为PB，则△KI值为0；

3）如果u（k）的值为NS，△u（k）的值为NB，则△KI值为0；

4）如果u（k）的值为NS，△u（k）的值为NS，则△KI值为NS；

5）如果u（k）的值为0，△u（k）的值为0，则△KI值为NM；

6）如果u（k）的值为PS，△u（k）的值为PS，则△KI值为PS；

7）如果u（k）的值为PM，△u（k）的值为PM，则△KI值为0。

积分环节主要功能为消除静态误差，提高无差度。积分环节主要对误差进行积分，不可避免的存在滞后性，△KI取值过大将增大系统的超调，严重可能引起振荡。所以，当u（k）值过大或过小时，△KI取0，只有当u（k）值适中时，积分环节的功能才得以体现。

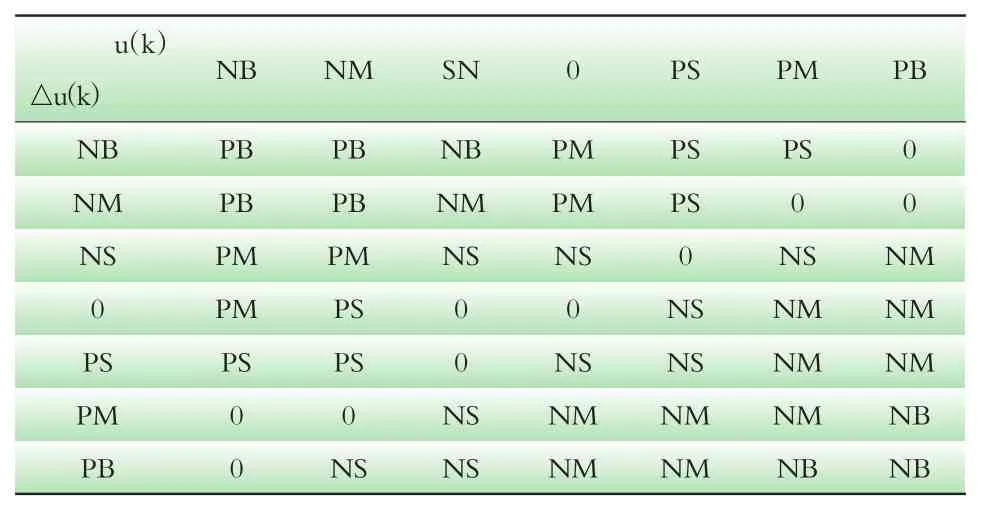
表1 △Kp的模糊规则

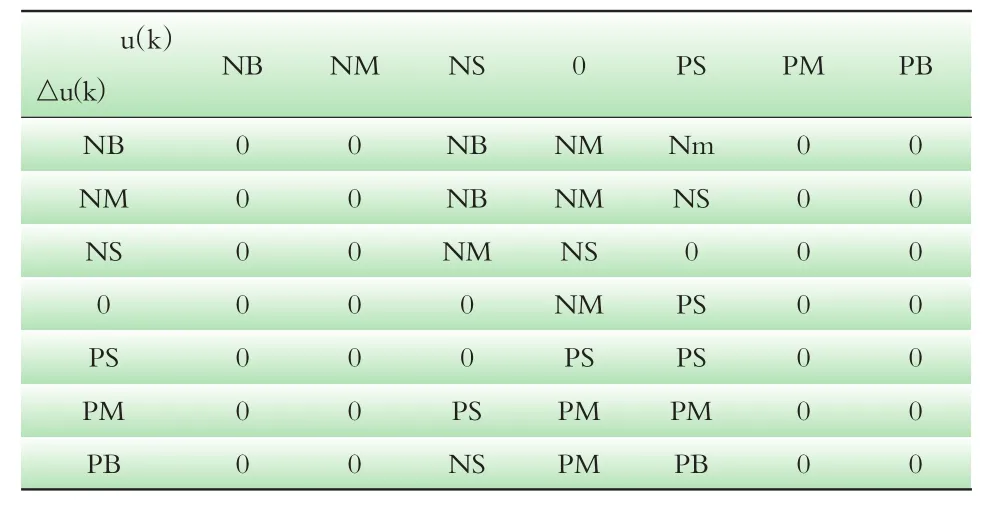
表2 △KI的模糊规则

3 实验结果

针对本文提到的改进型ip-iq算法的分频检测和模糊PI双闭环控制方法，为了验证这两种针对低压动态补偿装置的优化措施是否能达到预期效果，使用MAT⁃LAB搭建了仿真模型，参数为：系统电压380 V，直流侧电压为800 V，滤波电抗器0.3 mH，开关频率6.4 kHz，负载采用带电阻的可控整流器。

在未对负载谐波进行FFT分析的前提下，对负载电流进行5,7,11次谐波电流的检测和补偿，实验结果如下：

图5为补偿前的A相电压电流波形，可以看出负荷电流畸变严重，存在较多的低次谐波电流；图6为经过分频检测和模糊PI控制补偿后的A相电流波形，虽然电流还是存在少量毛刺，但主要的谐波电流（5,7，11次）都已补偿干净，且满足实际系统的谐波电流畸变标准；图7为直流侧的电压波形，直流侧能稳定在800 V，且超调很小，稳定后波动较小，体现出模糊PI控制的高鲁棒性。

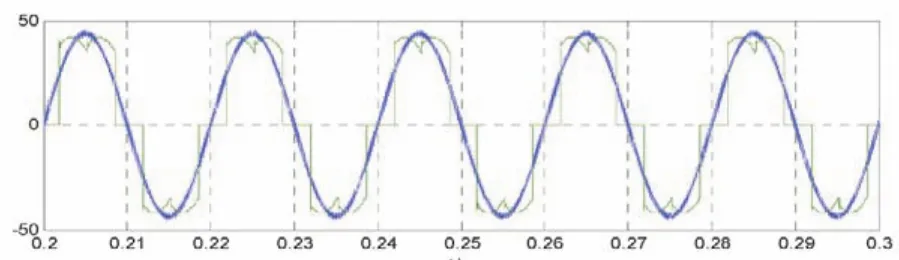
图5 补偿前A相电压电流

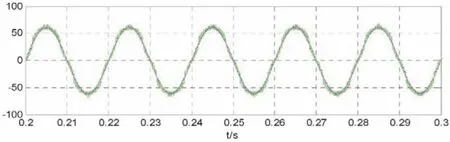
图6 补偿后A相电流

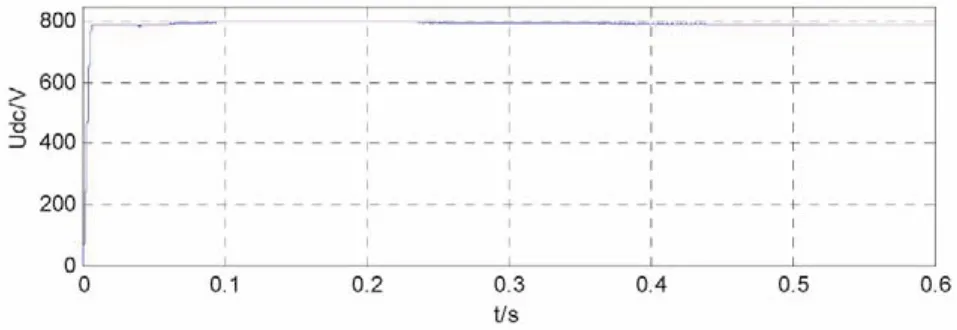
图7 直流侧电压波形

4 结论

由仿真结果可以发现，采用分频检测的补偿策略与模糊PI控制相结合的优化措施，能较好补偿系统谐波电流，可以达到为补偿无功节省容量的目的，同时有源滤波器响应速度快，超调较低，稳定性较好，都极大体现了这两种优化的可行性，达到优化的目的。

[1]王兆安，杨君，刘进军.谐波抑制和无功功率补偿[M].北京：机械工业出版社，2005.10.

[2]范瑞祥，罗安，涂春鸣.并联混合型有源滤波器的分频控制方法研究[J].中国电机工程学报，2007，27(25)：108-113.

[3]马伏军，罗安，帅智康，等.混合型有源电力滤波器的改进解耦型分频控制[J].电网技术，2010，34(12)，44-49.

[4]张超，杨耕，杜继宏.有源电力滤波器任意次谐波电流检测的新算法[J].电机与控制学报,2002,6(3):252-255.

[5]殷志柱，杨煜普，董祖毅，等.基于双闭环模糊控制的有源电力滤波器[J].电力系统保护与控制，2010,38(4):58-62.

[6]庄茂东，宋吉，王兴龙.多模块并联有源电力滤波器的性能[J].电能质量，2011,13:53-57.

[7]王立新.自适应模糊系统与控制——设计与稳定性分析[M].北京：国防工业出版社，1995.