一类斑块环境中三营养模型周期解的存在性
孟 超,周玉元
(湖南农业大学理学院,湖南长沙400128)
1 引言与预备知识
斑块环境中生态动力系统的性质是数学生态学的一个热点问题.许多学者对斑块环境中生态动力系统的持久性、稳定性与周期性做了大量的研究工作[1-10],但对各种群占有的斑块数量的变化规律研究很少.1994年,V.A.A.Jansen研究了一类斑块环境中三营养食物链模型分别在只有食饵扩散和只有捕食者扩散的情况下平衡点的存在性、稳定性[11].之后,段会玲研究了下列斑块环境中三营养模型的平衡点的存在性、稳定性[12]:

其中R表示空资源斑块的数量,N表示被食饵种群占领的资源斑块数量,M表示被食饵和捕食者同时占领的斑块,总资源斑块为N0(N0>1),且有R+N+M=N0,a>0,b>0,k>0,v>0.
本文将研究如下斑块环境中周期系统

正周期解的存在性,其中a(t),b(t),k(t),v(t)均为连续且严格正的ω周期函数.
为研究系统(2)的周期解,首先引入重合度理论中的延拓定理.
设X,Z是Banach空间,L:DomL⊂X→Z为线性映射,N:X→Z为连续映射,若L是指标为零的Fredholm映射,且存在连续投影P:X→X及Q:Z→Z,使得ImP=KerL,ImL=KerQ=Im(I-Q),则可逆,设其逆映射为KP,Ω是X中的有界开集,如果有界且KP(I是紧的,则称N在Ω上是L-紧的,由于ImQ与KerL同构,因而存在同构映射J:ImQ→KerL.
引理1[13]设L是指标为零的Fredholm映射,N在Ω上L-紧,如果
1)∀λ∈(0,1),方程Lx=λNx的解满足x∉∂Ω;
2)∀x∈KerL∩∂Ω,QNx≠0;
3)deg{JQN,Ω∩KerL,0}≠0.
则方程Lx=Nx在内至少存在一个解.

将R(t)=1-N(t)-M(t)代入上式,得

2 主要结果
考虑到系统(4)的生态意义,假定初始值N(0)≥0,M(0)≥0,易证={(y1,y2)T∈R2|y1≥0,y2≥0}关于系统(4)是正向不变的.
证明 作变换

则系统(4)化为下列等价系统:

取X=Y={x=(x1,x2)T∈C(R,R2):xi(t+ω)=xi(t),i=1,2}.定义范数,x=(x1,x2)∈X或Y.对∀x=(x1,x2)T∈X,由其周期性可知,

是一ω周期函数.
令L:DomL∩X→X,L(x1(t),x2(t))T=.则DomL={(x1(t),x2(t))T∈C′(R,R2)}.
定义映射:N:X→X,.易知KerL=R2,ImL为Y中的闭子集,且dim KerL=codim ImL=2.
又P,Q均为连续映射,因此,ImP=KerL,KerQ=ImL=Im(I-Q).从而L是一个指标为零的FredhoIm映射,通过计算知LP的逆KP存在,且KP:ImL→DomL∩于是

利用Lebesgue收敛定理可以证明QN及KP(I-Q)N是连续的.
设Ω是X中的有界开集,显然有界,利用Arzela-Ascoli[14]定理易证在Ω上是紧的,因此N在上是L-紧的.
对于算子方程Lx=λNx,λ∈(0,1),有

设x(t)=(x1(t),x2(t))T∈X是式(7),(8)关于某个特定的λ∈(0,1)的解.对(7),(8)在[0,ω]上积分,得

由式(7),(9)可得

即

由式(8),(10)类似可得

对于(x1(t),x2(t))T∈X,∃ξi,ηi∈[0,ω],使得


同时考虑式(11),对∀t∈[0,ω]有
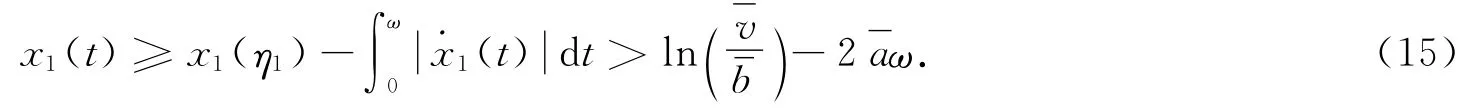

同时考虑式(11),对∀t∈[0,ω]有

由式(15)和(17)有

另一方面,由式(9),(13)及定理条件(i)可得

同时考虑式(12),对∀t∈[0,ω]有

由式(20)和(21)有

显然B1,B2与λ无关.
设w=(w1,w2)T∈R2,考虑代数方程组

当x∈∂Ω∩KerL=∂Ω∩R2时,x为R2中的常值向量且=B.则由B的定义知
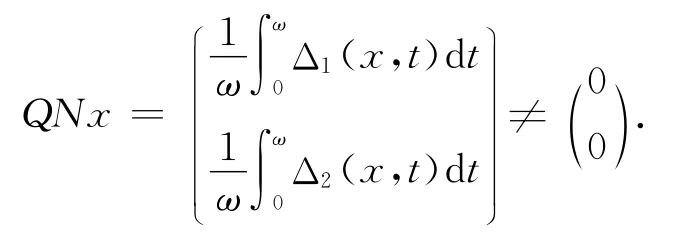
所以引理1中条件2)满足.
下面证明引理1中条件3)也满足.
因ImQ=KerL,取J为恒同映射,可直接计算得

故由引理1可知,方程Lx=Nx在DomL∩中至少存在一个解,即系统(6)在DomL∩中至少存在一个ω周期解,从而是系统(4)的一个ω周期正解.证毕.
[1]Cantrell R S,Cosner C,Lou Yuan.Evolutionary stability of ideal free dispersal strategies in patchy environments[J].Journal of Mathematical Biology,2012,65(5):943-965.
[2]Jansen V A A,Lloyd A L.Local stability analysis of spatially homogeneous solutions of multi-patch systems[J].Journal of Mathematical Biology,2000,41(3):232-252.
[3]Chen Lijuan.Permanence for a delayed predator-prey model of prey dispersal in two-patch environments[J].Journal of Applied Mathematics and Computing,2010,34(1/2):207-232.
[4]Qiu Lin,Mitsui T.Predator-prey dynamics with delay when prey dispersing inn-patch environment[J].Japan Journal of Industrial and Applied Mathematics,2003,20(1):37-49.
[5]Zhang Feng,Hui Cang,Han Xiaozhuo,etal.Evolution of cooperation in patchy habitat under patch decay and isolation[J].Ecological Research,2005,20(4):461-469.
[6]Chun Y S,Ryoo M I,Choi W I.Influences of resource patch distribution on a host-parasitoid system stability in patch environment:a laboratory study[J].Asia-Pacific Entomology,1998,1(2):223-234.
[7]Zhang Xu,Wang Wendi.Importance of dispersal adaptations of two competitive populations between patches[J].Ecological Modelling,2011,222(1):11-20.
[8]Wang Ruiping.Competition in a patch environment with cross-diffusion in a three-dimensional Lotka-Volterra system[J].Nonlinear Analysis:Real World Applications,2010,11(4):2726-2730.
[9]Tian Desheng.Periodic solution and persistence for a three-species ratio-dependent predator-prey model with time delays in two-patch environments[J].Journal of Systems Science and Complexity,2008,21(2):226-238.
[10]Zhang Long,Teng Zhidong,Liu Zijian.Survival analysis for a periodic predator-prey model with prey impulsively unilateral diffusion in two patches[J].Applied Mathematical Modelling,2011,35(9):4243-4256.
[11]Jansen V A A.Effects of dispersal in a tri-trophic metapopulation model[J].Journal of Mathematical Biology,1994,34(2):195-224.
[12]段会玲.斑块环境中三营养模型的动力学性态[J].重庆三峡学院学报,2008,24(3):64-67.
[13]徐炳祥,曾志军.一类具有Holling III型功能性反应的捕食者-食饵系统的周期解的存在性[J].纯粹数学与应用数学,2012,28(4):523-530.
[14]张恭庆.泛函分析讲义:上册[M].北京:北京大学出版社,2004:15-16.

