随机试验设计中缺失值插补方法研究

李 杰，张晓玲

（大理学院数学与计算机学院，云南大理 671003）

随机化区组试验设计中，由于试验样本退出试验、损坏、记录丢失等原因常常会产生缺失数据。缺失数据的处理方法最简单的是删掉缺失值，这种处理方法有两个缺点：①样本量减少，使得模型的标准误差增大，从而影响模型的精度；②丢失了珍贵的样本信息。为了克服以上两种缺点，可以采用插补的方法来填补缺失值。研究缺失数据插补和应用的文献有很多，现在也是一个研究热点。

帅平等〔1〕只对缺失数据的方法进行了综述，没有针对随机化区组试验设计给出缺失数据处理方法的建议；田兵〔2〕简单介绍了缺失数据的单一插补方法；庞新生〔3〕简单介绍了随机抽样、分层随机抽样条件下缺失数据多重插补的抽样推断方法；杨基栋〔4〕从理论上分析了缺失数据插补方法的方差和误差，没有给出模拟研究的例子；邓银燕〔5〕从回归分析的角度对缺失数据插补方法进行了实证分析，但是没有考虑实验设计中的随机化区组设计缺失数据的问题。郁文和郑明〔6〕研究了缺失数据的均值推断问题。在随机缺失及半参数模型的假设下,设计了基于影响函数理论的经验似然推断方法。此外，也有学者〔7-9〕从贝叶斯角度对缺失数据进行了研究；相关文献〔10-12〕从广义线性模型的角度对缺失数据进行了研究；还有学者〔13-15〕在数据挖掘方面对缺失数据造成的影响进行了研究；除理论研究外，部分学者对缺失数据插补方法进行了实例研究〔16-21〕。

通常有3种填补缺失值的方法：均值法、公式法和Yate’s法。均值插补的思想非常简单，即用观测样本的均值来插补缺失值，这种方法简单易行。公式法最初是由Allan和Wishart（1930年）在处理随机化区组试验中缺失数据时提出来的，其思想是用行和列的均值的组合进行插补。Yate’s法是由Yate于1933年提出来的，其基本思想是不考虑缺失值，仅对观测值进行线性回归，然后根据回归模型对缺失部分进行预测，用预测值代替缺失值。

直接删除缺失数据法和3种缺失值插补方法哪一个好，所填补的缺失值引起的模型误差最小是一个很值得研究的问题。主要用随机模拟来研究4种方法的好坏，首先产生一个4×5的随机区组设计，其次指定的缺失值个数m，缺失位置的组合数有（m=1,…，6）个，对每一个不同的组合，分别研究4种方法回归的标准误差、可决系数和复可决系数，根据这3个指标的优劣来评价4种方法的好坏。

1 随机化区组试验设计及回归

1.1 随机化区组试验设计 在农业、社会、经济和科研中经常需要考察一个变量受一个或者几个变量的影响，例如在水稻种植试验中，不同的施肥量和灌溉量会影响水稻的产量，实验者想寻找最优的施肥量和灌溉量组合，使得水稻的单亩产量最大，这就需要试验设计。

假设变量y受到两个因素A和B的影响，因素A有t个水平，因素B有b个水平，因素A和B共有t×b个组合。变量y在每种组合下的观测值用yij（i=1，… ，t，j=1，… ，b）表示，一般用二维表来表示，见表1。

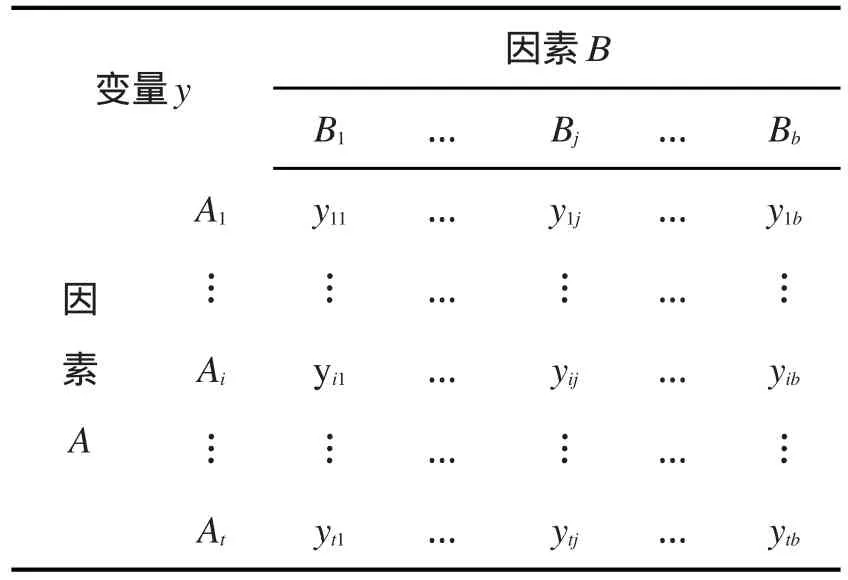
表1 变量y在双因素影响下的观测值

表1所示是试验设计中常见的双因素模型，对双因素模型，有很成熟的理论来进行分析，实质上它是一种线性回归。

1.2 线性回归 用线性回归的理论进行建模，重点在于构造相应的设计矩阵。表1中变量y共有t×b个，因素A和B不同的水平数共有t+b个，构造设计矩阵的主要思想就是把因素A和B的每个水平看成一个二元变量，用0和1表示。设计矩阵的形式要根据变量y排列的形式，变量y可以按行，或者按列拉直，不失一般性，变量y约定按行拉直。即

Y= （y11…y1j…y1b…yi1…yij…yib…yt1…ytj…ytb）T。

根据线性回归理论，设计矩阵变量的个数应该为t+b－1个，前t个变量为因素A的各个水平，后b-1个变量为因素B的前b-1个变量，设计矩阵用X表示。设计矩阵的取值依据变量y而定，例如变量y的第i×j个变量yij对应的设计矩阵X第i×j行的取值为：Ai变量对应的位置取值为1，Bj变量对应的位置取值为1，其余位置都取为0，即（0，…，1，…，1，…，0），假设t=b=2，设计矩阵可以表示为：

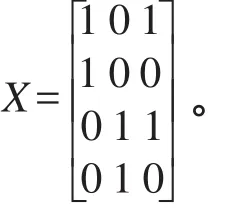
线性模型可以表示为：

其中，β是回归系数向量，ε=（ε11…εij…εtb），εij独立同分布，均值为0，方差为1。

2 插补方法

对于完全数据，可以用线性回归理论的方法建模。当表1中某一个或几个单元格数据缺失时，线性模型就不再适用。一个朴素的想法：把缺失的部分填补起来，然后再用线性模型进行分析。填补的方法有很多种，这里只涉及到3种。

均值插补：假设数据共有n个，其中有m个缺失值，观测到的数据有n－m个，均值插补的方法就是用n－m个观测数据的均值来填补m个缺失值。填补后再用线性模型进行分析。

公式法：由Allan和Wishart（1930年）在处理随机化区组试验中缺失数据时提出来的。假设表1中第i行第j列的数据缺失，填补该处缺失值的方法是：

Yate’s法：用n表示全部数据的个数，m表示观测数据的个数，n-m为缺失数据，Yate’s方法的基本步骤是：

1）用m个观测数据进行建模；

2）估计模型的参数；

3）用模型来预测n-m个缺失值；

4）把n-m个缺失值的预测值作为插补值；

5）运用补全的n个数据进行建模；

6）重复3-5步，直到插补的值收敛为止。

这3种方法使用时各有优劣，用以评价优劣的标准是回归标准误差、可决系数和复可决系数。可决系数是衡量自变量与因变量关系密切程度的指标，表示自变量解释了因变量变动的百分比，用R2表示，其公式是：

而复可决系数同可决系数一样是衡量回归优劣的指标，但复可决系数消除了变量个数的影响，可以用于不同变量个数模型间的比较，其公式是：

其中n是样本量，m是自变量的个数。

3 模拟研究

模拟研究所用的分析软件是R软件，后面所有的编程程序都是用R语言编写的。首先设计一个随机化区组实验。A因素有4个水平，B因素有5个水平，即t=4，b=5。对于A因素的第一个水平，产生5个服从均值是2，方差是1的正态随机数；对于第二个水平产生5个服从均值是4，方差是1的正态随机数；对于第三个水平产生5个服从均值是6，方差是1的正态随机数；对于第四个水平产生5个均值为8，方差为1的正态随机数；而对于因素B，产生的随机数的方法同A类似，只不过B因素每一个水平产生正态随机数的均值为1,3,5,7,9，方差都为1。因素A和B各产生了20个随机数，变量y的值通过如下方法确定：

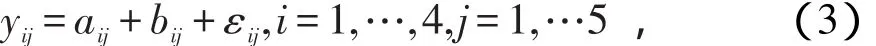
其中εij是服从均值为0，方差为1的正态分布。产生的数据见表2。

表2 随机产生的双因素实验设计

表2中的数据是依据（3）式进行计算的，接下来的模拟计算完全依据表2中产生的数据。下面进行缺失方法介绍。

表2中共有20个单元格，要进行缺失值模拟研究，需具备两种条件：缺失值的个数和缺失值的位置。缺失值的个数m拟定为1,2,3,4,5,6个，不同的缺失值个数对应着不同的缺失位置数，当缺失值个数m=1时，缺失的位置共有个；缺失值个数m=2时，缺失的位置共有个；缺失值个数m=3时，缺失的位置共有个；缺失值个数m=4时，缺失的位置共有个；缺失值个数m=5时，缺失的位置共有个；缺失值个数m=6时，缺失的位置共有个。考虑到计算机内存和程序计算的复杂性，m只取到6。

对每一个确定的缺失值个数m和与其对应的缺失位置组合数mi，在每一种缺失位置情况下计算删除缺失值回归、均值插补回归、公式插补回归和Yate’s插补回归4种回归的标准误差、可决系数和复可决系数，只到mi个缺失位置的情况全部遍历为止。图1所示的是缺失个数不同的情况下，4种方法标准误差的箱型图。从图1中可以看出Yate’s方法是这4种方法中最好的，标准误差明显比均值插补和公式插补要好，表现最差的是均值插补方法。图2所示的是在不同的缺失值个数下，4种方法可决系数均值的折线图。因可决系数和复可决系数在模拟结果中非常接近，故只研究可决系数。

图1 不同缺失值个数下4种插补方法标准误差的箱型图

图2 不同缺失值个数下4种插补方法可决系数均值折线图

综合图1箱型图和图2可决系数折线图的分析，可以得出Yate’s方法插补的标准误差和可决系数表现是4种方法中最好的；随着缺失值个数的增加，公式法和删除法的可决系数有下降的趋势。

4 实例

下面这个例子来自于Snedecor和Cochran（1967年）的例子，该例子是一个5×5的拉丁方设计，其中3个数值缺失，表中的数据表示的是小米的产量数据，“—”表示缺失，见表3。

表3 小米的产量数据

对表3中的数据分别运用前面4种方法进行分析，得到的结果如下：直接删除缺失值方法得到的标准误差是32.72，可决系数是0.9904，复可决系数是0.9838；均值插补方法的回归标准误差是35.27，可决系数是0.9879，复可决系数是0.9811；公式插补方法的回归标准误差是30.65，可决系数是0.9904，复可决系数是0.985；Yate’s插补方法的回归标准误差是29.49，可决系数是0.9912，复可决系数是0.9862。Yate’s插补方法的各项指标都优于其它三种方法,用Yate’s方法得到插补的值分别是（194.7434,236.0789,165.9934）。

5 结论

在随机化区组实验设计中，有4种方法可以进行缺失值处理：第一种方法是删除缺失的案例，只对观测的数据进行回归；第二种方法是利用观测数据的均值进行插补，填补缺失值；第三种方法是利用公式法对缺失的部分数据进行插补；第四种是根据Yate’s方法进行插补。这4种方法各有优劣，在样本量足够的情况下，可以考虑直接运用观测数据进行回归，或者采用均值插补。公式法插补较为麻烦，计算量最大的应该是Yate’s插补，因为Yate’s插补需要进行迭代，计算量比其他三种方法要大，也较为耗时。就回归标准误差和可决系数而言，Yate’s插补方法是4种方法中最好的，尤其是在样本量较少的情况下，建议使用Yate’s插补方法。

〔1〕帅平,李晓松,周晓华,等.缺失数据统计处理方法的研究进展〔J〕.中国卫生统计,2013,30（1）:135-142.

〔2〕田兵.缺失数据的单一插补方法〔J〕.阴山学刊：自然科学版,2011,25（3）:17-19.

〔3〕庞新生.缺失数据插补处理方法的比较研究〔J〕.统计与决策,2012（24）:18-22.

〔4〕杨基栋.缺失数据的插补方法及其统计分析〔J〕.华北水利水电学院学报,2010,31（2）:98-103.

〔5〕邓银燕.缺失数据的填充方法研究及实证分析〔D〕.西安：西北大学,2010.

〔6〕郁文,郑明.缺失数据均值推断的经验似然方法〔J〕.数学年刊,2010,31A（1）:71-80.

〔7〕胡思贵,赵明.完全随机缺失数据下配对试验的Bayes分析〔J〕.数学的实践与认识,2011,41（8）:73-77.

〔8〕和燕,彭燕梅,唐年胜.带不可忽略缺失数据的再生散度随机效应模型的Bayes估计〔J〕.宁夏大学学报:自然科学版,2011,32（3）:193-197.

〔9〕胡芳芳.缺失数据的贝叶斯模型处理〔D〕.长沙：中南大学,2011.

〔10〕汪金晖,张淑梅,辛涛.缺失数据下等级反应模型参数MCMC估计〔J〕.北京师范大学学报:自然科学版,2011,47（3）:229-234.

〔11〕邓明.基于GMM的缺失数据回归模型的半参数估计〔J〕.统计与信息论坛,2013,28（3）:9-15.

〔12〕陈盼盼.缺失数据下半参数变系数部分线性模型的统计推断〔D〕.北京：北京工业大学,2012.

〔13〕方匡南,谢邦昌.基于聚类关联规则的缺失数据处理研究〔J〕.统计研究,2011,28（2）:87-92.

〔14〕张宙锋,张磊,王志超.改进的数据流缺失数据处理算法〔J〕.微电子学与计算机,2012,29（3）:55-59.

〔15〕纪燕霞.数据挖掘中处理不完全数据的类均值方法及其扩展〔D〕.西安：长安大学,2010.

〔16〕曾洁美.数据缺失处理在“绿色矿山”中的应用〔D〕.马鞍山:安徽工业大学,2012.

〔17〕张熙.多重填补方法估计存在不依从与缺失值的随机对照试验的因果效应〔D〕.上海：复旦大学,2012.

〔18〕廖娟芬,黄绍军,李春红.具有部分缺失数据的异均值方差分析法〔J〕.海南师范大学学报：自然科学版,2011,24（1）:9-11.

〔19〕游晓锋,丁树良,刘红云.缺失数据的估计方法及应用〔J〕.江西师范大学学报:自然科学版,2011,35（3）:325-330.

〔20〕岳春柳.缺失数据的概率主成分分析〔D〕.长春：东北师范大学,2010.

〔21〕余竞,钟涵宇,刘利,等.统计调查表缺失数据插补效果的实证分析〔J〕.成都大学学报：自然科学版,2010,29（4）:307-310.