有限元实验课程教学探索

黄鹏展

（新疆大学数学与系统科学学院,乌鲁木齐 830046）

众所周知,大量实际中的工程问题都可以用偏微分方程来描述,但有许多偏微分方程定解问题的解不能以实用的解析形式来表出,从而无法得到这些方程的准确解,以定量地描述客观过程。有限元课程是数值分析的后继课程,是计算数学专业学生必修的专业课程。课程中的有限元方法在数值计算的理论基础上,构造求解的近似逼近方法。该课程通过一些典型、常用、有效的数值方法来解释有限元方法的基本思想,使学生了解如何在计算机上应用这些数值方法求解一个偏微分方程定解问题。同时,通过对有限元基本概念及基本理论的学习,使学生的理论分析能力得到一定的训练,并通过学习与实践使得学生熟练掌握及运用有限元方法来数值求解偏微分方程。

而有限元实验课程的设立,则能更好地为学生学习有限元服务,使得学生能够更好、更深刻地了解有限元方法,体会有限元方法在数值求解偏微分方程时的魅力。本文主要结合笔者的亲身教学经历,从有限元的Matlab工具包、有限元软件Free⁃fem++以及Matlab编程等三个方面来探索有限元实验课程的教学方法。这三个方面从简到难、从特定偏微分方程类型求解到较一般偏微分方程求解,循序渐进地引导学生进行有限元方法的实践和数值的实验。

1 有限元方法

本文以文献〔1〕中的一个偏微分方程为例,简单地介绍基本的有限元方法。

考虑二维区域上的Poisson方程〔2〕第三边值问题

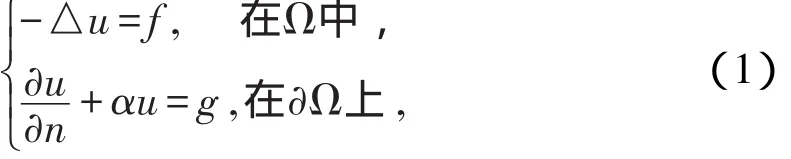
这里的Ω∈R2是具有光滑边界的有界凸区域,n是∂Ω上的外法线方向,α和g是∂Ω上的连续函数,α=α(x,y)≥0,△是拉普拉斯算子,f是作用力。为简便起见,在后面的计算部分,令 f=g=α=1,计算区域Ω取成单位正方形。

我们知道有限元方法基于变分原理,故先给出方程（1）的变分形式。即第一步,

第二步,给出计算区域的网格剖分。设h是一个趋近于0的正参数,记网格剖分为Kh,它由一些三角单元K组成。

第三步,试探函数空间的构造。即选取有限元子空间

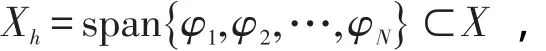
其中, φi（i=1,2,…,N）是基函数,满足

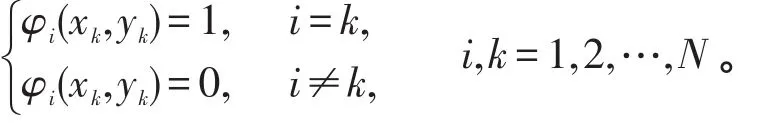
求使得，D(uh,vh)=F(vh),∀vh∈ Xh，

其中ui=u(xi,yi)。

第四步,有限元离散。生成单元刚度矩阵和单元荷载向量,通过单元上局部编码与整体编码的对应关系得到的扩张矩阵,生成总刚度矩阵和总荷载向量,然后对约束条件进行处理,最后得到有限元方程组。由方程组的求解方法解出ui,结合基函数φi得到有限元近似解uh。

2 有限元上机实验

有限元课程是一门计算数学专业中较难的课程,故而,我们首先对问题（1）使用较为简单Matlab工具包来实现数值模拟,鉴于它的可视化操作,学生易于上手。从而,增强他们对这门较难课程学习的信心,克服学习前的恐惧心理和由此产生的怠学状态。通过Matlab工具包对特定方程的模拟,能够使学生了解所求得方程的解到底是什么样子,初步了解有限元解法的过程。接着,采用有限元软件Freefem++来数值求解问题（1）,该有限元软件只需要写出有限元的变分形式即可。最后,按照有限元编程的框架图,使用Matlab来编制有限元求解（1）的程序。

2.1 Matlab工具包 根据文献〔3〕中的讲解,笔者以（1）为例,对Matlab工具包求解偏微分方程进行介绍。

第一步,打开Matlab软件,在命令框中输入pdetool,便可启动一个可视化界面。接着,完成求解区域的构造。

第二步,选取边界,打开Boundary Condition对话框,输入（1）中的第三类边界条件。

第三步,选择PDE Mode命令,设置方程的类型,这里为椭圆型方程,接着输入（1）中偏微分方程的系数。

第四步,利用Initialize Mesh命令,对第一步构造的求解区域进行网格剖分。如果网格不够密,可以利用Refine Mesh命令进行加密。

第五步,选择Solve PDE命令,求解设定的偏微分方程适定问题,给出数值解uh的图形,见图1。

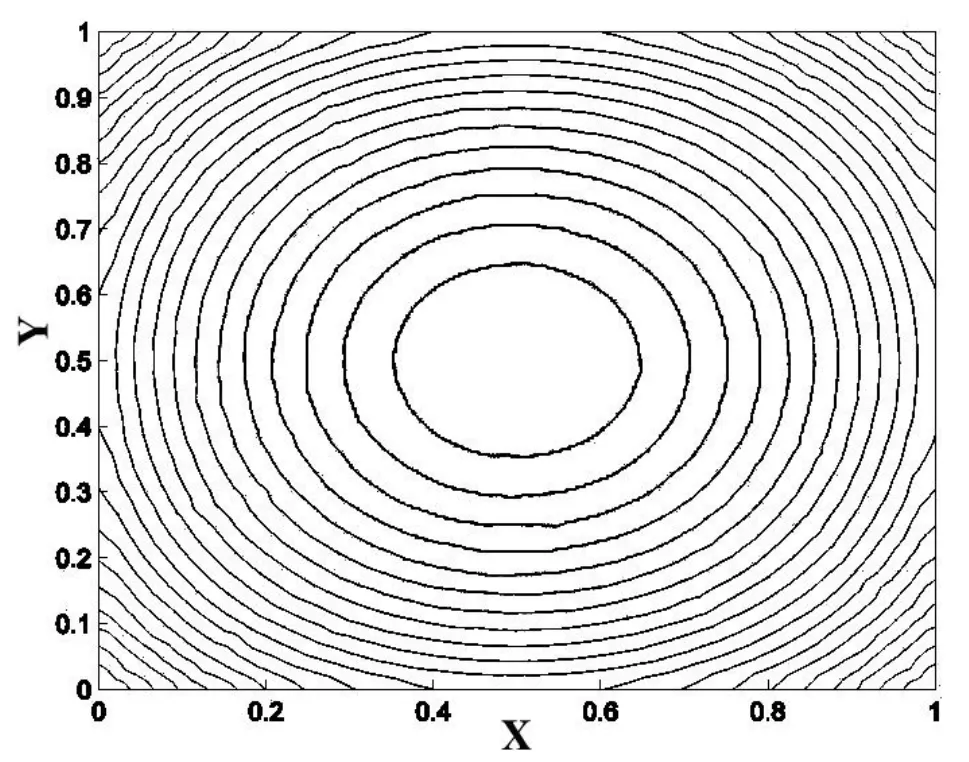
图1 用Matlab工具pdetool得到（1）的有限元解

Matlab工具包可以对空间二维问题快速高效求解。由于它的界面可视化,学生只需要使用用户界面,构造出求解区域,输入方程的类型和边界条件,自动生成网格,不需要人工设定基函数,就可以显示出数值解的结果。故而,它是一种利用有限元方法数值求解偏微分方程的简单有效工具。但是这个可视化界面只是对特定的一些方程,并且边界条件的设置也很固定。最主要的是不能够自己选择基函数或者构造基函数,而有限元的魅力主要正是在于它所拥有的各式各样的基函数,并可以根据自己的需要进行构造。

故而,Matlab工具包只适合有限元方法的初学者,使他们较好较快地了解求解偏微分方程的有限元方法。在这方面,自然地它有不可替代的优势。因此,笔者在有限元实验课程教学时,最初几节课,主要就是给学生们讲解Matlab工具包求解偏微分方程。

2.2 有限元软件 FreeFem++ FreeFem++〔4〕是一款数值求解偏微分方程的有限元软件。就像它名字所说的,它是一款免费的软件,可以直接在http://www.freefem.org这个网站上下载安装包,并自带它的教程。FreeFem++不是一个工具包,而是一个完整的有限元产品,具有内存需求少、计算速度快、易学好用、功能强大、应用面广等特点〔5-8〕。故而,在有限元实验课程随后的课时中,笔者将讲授这部分的内容。

仍以（1）为例,对有限元软件FreeFem++求解偏微分方程进行介绍。以下部分就是用该软件实现数值求解的FreeFem++程序,附程序注释。

real n=80;//设置网格尺度

mesh Th=square（n,n）;//生成网格

fespace Xh（Th,P2）;//定义有限元空间

Xh u,v;//声明试探函数和检验函数

func f=1;//选取作用力函数

solve Poisson（u,v）=//定义偏微分方程,即变分形式

·马改户 曹春生 何鄂 陈云岗 黎明 郭北平杨参军 白羽平 冷军 朱春林等10位雕塑、油画大家力挺学术邀请展

int2d（Th）（dx（u）*dx（v）+dy（u）*dy（v））//双线性项形式

+int1d（Th）（u*v）//D（u,v）的第二部分,系数为1

-int2d（Th）（v）//右端项

-int1d（Th）（v）;//F（v）的第二部分,g取1

plot（u,ps=“fig2.eps”）;//计算结果的可视化这样就完成了采用FreeFem++软件求解（1）的全部过程,数值结果见图2。

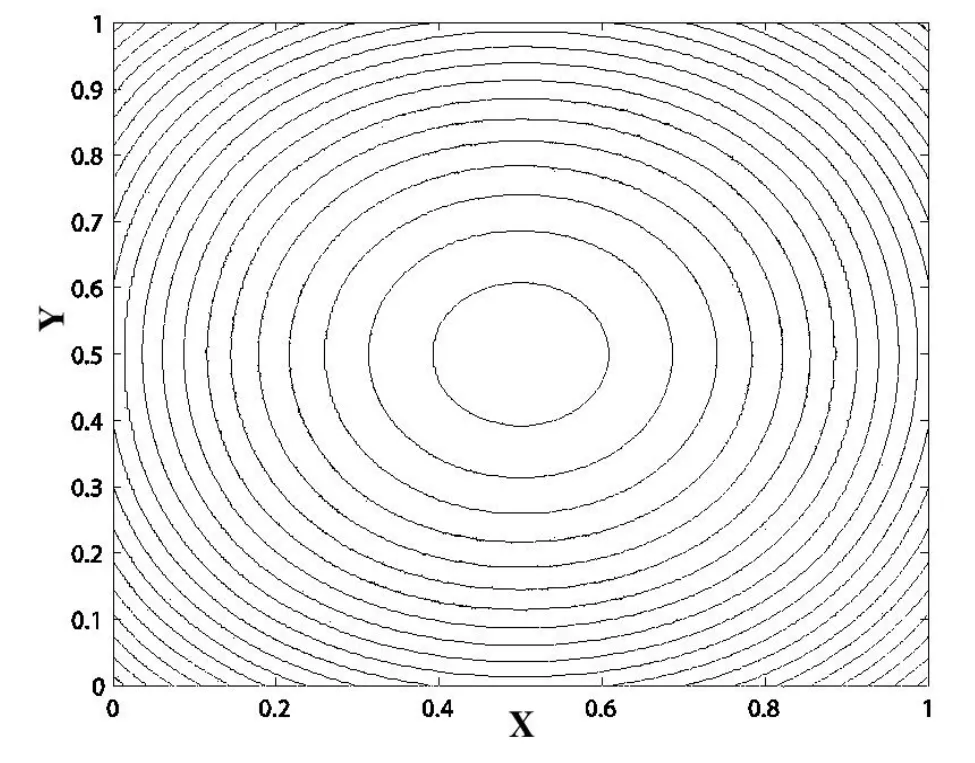
图2 利用FreeFem++软件得到（1）的有限元解

由以上的程序我们可以看到,使用该软件进行编程数值求解偏微分方程时,只需要写出原问题的变分问题即可,无需进行单元局部和总体的编号、单元刚度矩阵和单元荷载向量的计算、总刚度矩阵和总荷载向量的组成、有限元线性方程组的求解等具体过程。更加主要的是采用“fespace Xh（Th,P2）”这段语句就完成了有限元空间的定义,并且使用“int2d（Th）”这个命令就实现了数值积分的功能。寥寥数行即完成了对Poisson方程第三类边值问题的有限元方法求解。对比使用C或者Matlab编程需几百行的代码,FreeFem++程序大大节约了编程时间。

但是,由于它是一款免费软件,其底层语言没有公开,继而我们无法了解最本质的内容。故而,它有一定的局限性,无法对底层的代码进行修改,二次编程。并且,只能选取它所给定的一些基函数和有限元空间。因此,它适合一些想使用有限元方法做一些初步研究的研究生。如果想要验证更加原创的一些有限元算法,笔者认为应该利用C或Matlab或者Fortran语言来实现。

2.3基于Matlab的有限元编程 鉴于以上考虑,笔者在这门课程的剩余课时里,重点讲解基于Matlab的有限元方法编程。主要是根据文献〔9-10〕中的程序框图进行程序编制,仍旧以（1）为例。

M文件1:构造基函数 function J=Base（m,n），m,n分别是x,y轴等分点数。

M文件2:构造矩阵function A=juzhen（n,m），即构造求解未知节点所满足的矩阵。这里为重点部分,矩阵由总刚度矩阵并利用数值积分得到。

M文件3:当f=1时矩阵的右端项function b=youduanxiang（n,m）。

M文件4:将求出的矩阵变换为一般的矩阵function B=bh（n,m），即将矩阵A转换成与理论分析时计算的矩阵一样。

M文件5:右端项为1时,用CG方法求解矩阵function u=gonge（n,m,detla,max），这里,max为最大循环次数,detla=1.0E-6为容许误差。

M文件6:右端项为1时,用有限元方法得到的解 U=qiujie（n,m,detla,max）。

再利用一个主文件调用以上的M文件,给定所设的参数,就可以得到（1）的有限元方法数值解,见图3。

图3 利用Matlab编程得到（1）的有限元解

故而,利用文献〔9〕、〔10〕里面的程序框架图,我们可以编制有限元的Matlab程序,从而得到想要的数值结果。直接编程的主要优点就是算法验证的灵活性,可以任意构造希望的基函数及有限元空间。但是它所花费的时间最长,因编制程序以及调试程序等都得消耗大量的时间。

3 结论

本文结合笔者的教学经历,对有限元实验课程教学进行了探索。针对数值求解偏微分方程,主要关于Matlab工具包、有限元软件Freefem++以及Matlab有限元编程这三个方面展开讨论。具体介绍了这三种方法的使用和编制,给出了每种方法的优缺点。

总之,对有限元实验课程的教学要循序渐进。Matlab工具包最为简单适合初学者使用,但是对于求解的问题具有局限性;有限元软件Freefem++次之,但是对基函数选取与构造等方面的灵活性欠缺,故它适合成为研究生用来做一些初步研究的有效工具;Matlab有限元编程相比之下最为困难与耗时,但它是验证一些有限元原创算法的必备工具。

〔1〕陆金甫,关治.偏微分方程数值解〔M〕.2版.北京:清华大学出版社,2004.

〔2〕刘相国,谢如龙,郝江锋.二维泊松方程的交替方向迭代法〔J〕.大理学院学报,2010,9（10）:1-5.

〔3〕陆君安,尚涛,谢进,等.偏微分方程的MATLAB解法〔M〕.武汉:武汉大学出版社,2001.

〔4〕Hecht F.FreeFem++〔EB/OL〕.（2012-03-16）〔2012-10-10〕.http://www.freefem.org/ff++.

〔5〕尚月强.FreeFem++与偏微分方程有限元数值计算〔J〕.贵州师范学院学报,2012,27（12）:1-5.

〔6〕尚月强.基于MPI+FreeFem++的有限元并行计算〔J〕.软件导刊,2012,11（2）:27-29.

〔7〕杜世森.基于FreeFEM++的一阶有限元解法〔D〕.长沙:湖南大学,2011.

〔8〕詹阳烈,庄春刚，熊振华，等.基于水平集方法与Free⁃FEM的弹性结构拓扑优化〔J〕.中国机械工程,2009,20（11）:1326-1331.

〔9〕李开泰,黄艾香,黄庆怀.有限元方法及其应用〔M〕.北京:科学出版社,2006.

〔10〕马逸尘,梅立泉,王阿霞.偏微分方程现代数值方法〔M〕.北京:科学出版社,2006.