基于灰色神经网络和支持向量机的两相流流型辨识

李精精 周 涛 段 军 张 蕾

(华北电力大学核热工安全与标准化研究所 北京 102206)

在气液两相流中，流型的不同影响了两相流的流动特性和传热传质性能，两相流中流量、空隙率等参量的测量也依赖于流型。因此，两相流流型的识别成为两相流一个重要的研究方向[1]。两相流的压差波动信号含有不同流型的丰富信息，成为流型辨识的重要参量。李菊等[2]利用mallat小波多尺度分解的方法研究了段塞流与波状流的特征。黄竹青等[3]从Lipschitz奇异性的定义出发，根据信号与噪声的奇异性指数a的不同，推导出不同流型a值的大小，利用 Lipschitz指数区分不同流型。Nguyen等[4]利用小波分析方法研究含气率的变化，以区分不同流型。小波神经网络作为一种智能技术已经在分类辨识中得到了广泛应用[5,6]。孙斌等[7]利用小波包分解对流型的动态压差波动信号进行分析、提取特征，然后将小波包能量特征与Kohonen神经网络结合进行流型识别。ZHANG等[8]利用支持向量机分析了油气两相流的流型辨识，得到了较好的效果。龙军等[9]利用经验模态分解的小通道气液两相流数据输入最小二乘支持向量机，发现这种方法可以提高预测精度。TAN等[10]利用基于电阻层析成像的支持向量机方法进行了气液两相流的流型辨识。目前，已有文献多是对压差波动信号进行小波分析[1–3,5–7]，然后将小波能量数据进行归一化处理，处理后的数据通过神经网络进行流型辨识。张毅等[11]结合灰色模型和神经网络对数据处理的优点，提出了并联型和嵌入型灰色神经网络机床热误差预测模型，目前还没有人利用灰色神经网络进行流型的辨识。利用支持向量机进行流型辨识时，多是利用经验模态分解的方法对数据进行处理，然后通过最小二乘支持向量机进行分类处理，尚无出现将小波能量数据和压差波动数据输入 Lib-SVM 进行气液两相流的流型辨识。

1 研究方法

1.1 灰色神经网络

首先利用db1小波对信号进行5尺度分解，提取多尺度小波变换的小波系数。小波能量表达式为：

BP神经网络拓扑结构如图1所示。嵌入型灰色神经网络数据处理过程如图2所示。

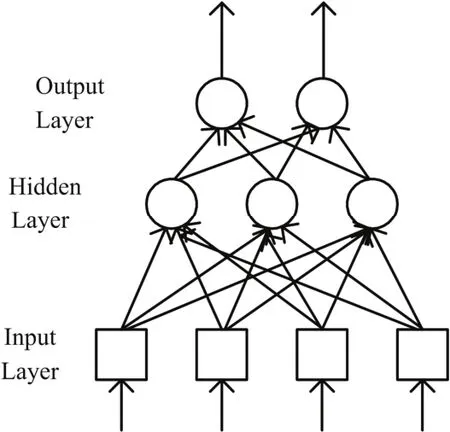
图1 BP神经网络拓扑图Fig.1 BP neural network topological graph.

图2 嵌入型灰色神经网络数据处理过程Fig.2 Implant gray neural network data treating processes.

如图1所示，网络共有三层。输入层中的每个输入都馈送到了隐藏层，作为该层每一个神经细胞的输入；然后，从隐藏层的每个神经细胞的输出都连到了它下一层(即输出层)。理论证明[12]对于三层的BP神经网络可以完成任意维的数据转换。

图2即是借鉴了灰色系统理论对BP神经网络的拓扑结构进行改造。强化BP神经网络对数据的处理能力，加快运算速度，增强模型的容错能力。在BP神经网络的输入层前增加一个灰化层，其作用是将原始数据按照式(3)作累加处理，生成新的数据序列，有效弱化原始数据的随机性。由于一次累加序列是单调递增的，有利于发挥BP神经网络的非线性拟合作用，网络学习时间减少，在增加预测精度的同时也加快了收敛速度。

设有时间序列：

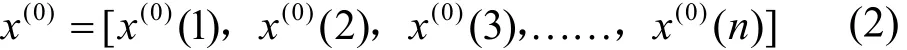
作一阶累加：

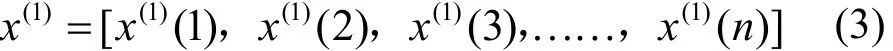
1.2 支持向量机

SVM是基于结构风险最小化的统计学习方法，具有完备的统计学习理论基础和出色的学习性能，在模式识别和函数估计中得到了有效的应用。Lib-SVM作为通用的SVM软件包，包含了5种SVM类型，可以解决分类问题、回归问题以及分布估计等问题。SVM从线性可分情况下的最优分类面发展而来。最优分类面即要求分类线不但能将两类正确分开(训练错误率为 0)，且使分类间隔最大。SVM考虑寻找一个满足分类要求的超平面，并且使训练集中的点距离分类面尽可能的远，也就是寻找一个分类面使它两侧的空白区域(margin)最大，w是权重向量。过两类样本中离分类面最近的点且平行于最优分类面的超平面上H1、H2的训练样本称作支持向量，如图3所示。

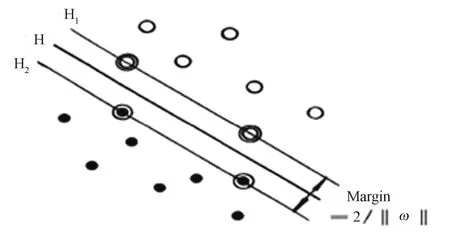
图3 最优分类超平面Fig.3 Optimal classify hyperplane.

1.3 处理方法

对于灰色神经网络方法，目前还没有用于气液两相流流型的辨识中。本研究将小波提取的21组小波能量作为特征向量，经过灰化层的处理后输入灰色神经网络，选用三层BP神经网络进行训练。数据的输出为T：泡状流(0 0 0 1)、环状流(0 0 1 1)、间歇流(0 1 1 1)。选用9组数据作为测试数据，其中包括泡状流、环状流、间歇流各3组。

对于支持向量机的方法，文献[8–10]是利用经验模态分解的方法对数据进行处理，处理后的数据一般通过最小二乘支持向量机(LSSVM)进行分类处理。本研究选取21组小波能量数据，作为训练数据输入Lib-SVM进行训练。其中泡状流用1表示，环状流用2表示，间歇流用3表示。选用9组数据作为测试数据，其中包括泡状流、环状流、间歇流各3组。将小波分析得到的能量信号作为Lib-SVM的输入，将流型作为Lib-SVM的标签，对气液两相流的压差波动信号进行分类处理。

训练数据共1200组，其中泡状流400组，环状流400组，间歇流400组。测试数据共147组，其中泡状流49组，环状流49组，间歇流49组。

2 研究对象

王强等[13]进行了气液两相流的实验，实验中气液两相流的压差信号由 PD-2型差压变送器进行测量，并由IMP3595数据采集板进行采集。实验参数范围为0.1–0.5 MPa，工质温度为3ºC–42ºC，空气流量为0–25 m3/s，水的流量为0–4.5 m3/s。实验数据如图4所示，其中n为采样序列。

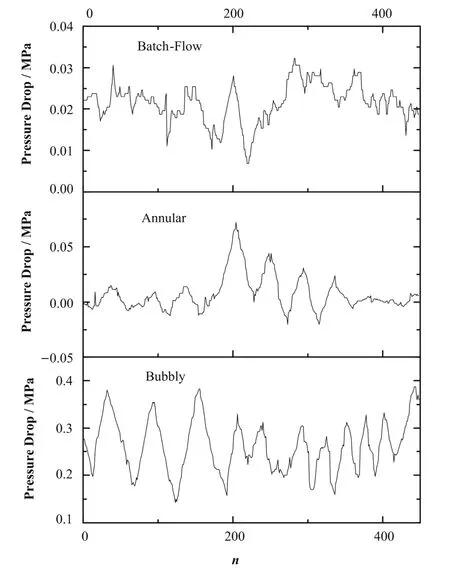
图4 各流型压差图Fig.4 Pressure drop of different flow pattern.

图4中选取了实验数据中的泡状流、环状流和间歇流。气液两相流的压力波动信号特征由低频部分和高频部分组成[14]。低频大尺度波动反映了系统的整体性质，但是高频部分也包含了大量的信息。

3 结果与分析

3.1 嵌入式灰色神经网络预测结果

嵌入型灰色神经网络方法与BP神经网络检测数据的对比结果如表1所示。

由表1可知，接近真实流型的向量其精确度相对较高。以第1组和第8组数据为例进行分析。对于第1组数据，真实流型为(0 0 0 1)，BP检测结果为(–0.002 0.014 –0.020 1.000)，嵌入型灰色神经网络的检测结果为(–0.046 –0.098 0.092 1.080)，可以看出对于第1组数据，两种方法检测结果均很好。对于第8组数据，真实流型为间歇流(0 1 1 1)，BP检测结果为(–0.0106 0.521 1.021 1.050)，嵌入型灰色神经网络的检测结果为(–0.009 0.811 0.9747 1.001)，对比两组数据可知，嵌入型灰色神经网络的检测结果比BP网络检测结果精确。通过对表 1的整体分析可知，加入灰化层后，神经网络对数据的处理结果比未加入灰化层时的预测数据更准确，对流型的辨识结果更好，而且明显减少了数据边缘化的效果，避免了单一模型丢失信息的缺憾，可以更准确的实现流型辨识。

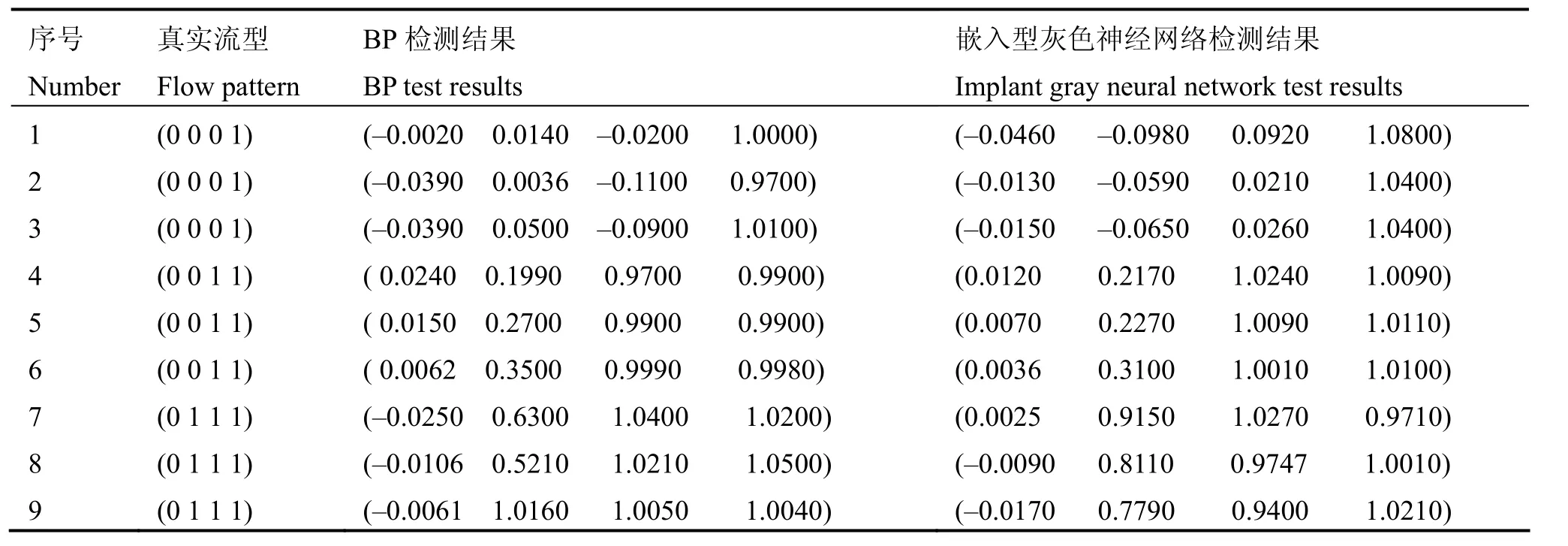
表1 嵌入型灰色神经网络与BP神经网络测试结果Table 1 The test results of implant gray and BP neural network.

3.2 小波支持向量机预测结果

小波能量数据输入Lib-SVM、BP神经网络、嵌入型灰色神经网络检测结果对比如表2所示。

将小波能量数据输入 Lib-SVM可以完成对流型的精确辨识。由表2可知，Lib-SVM和嵌入型灰色神经网络对三种流型辨识结果都比较准确。以环状流中的第6组数据为例，嵌入型灰色神经网络的检测结果为环状流(0.0036 0.3100 1.0010 1.0100)，对于向量中的第二个元素，数据为0.3100，与真实泡状流中的0具有一定的差异。因此嵌入型灰色神经网络在检测数据上存在一定的误差，Lib-SVM对各种流型的检测结果更准确。

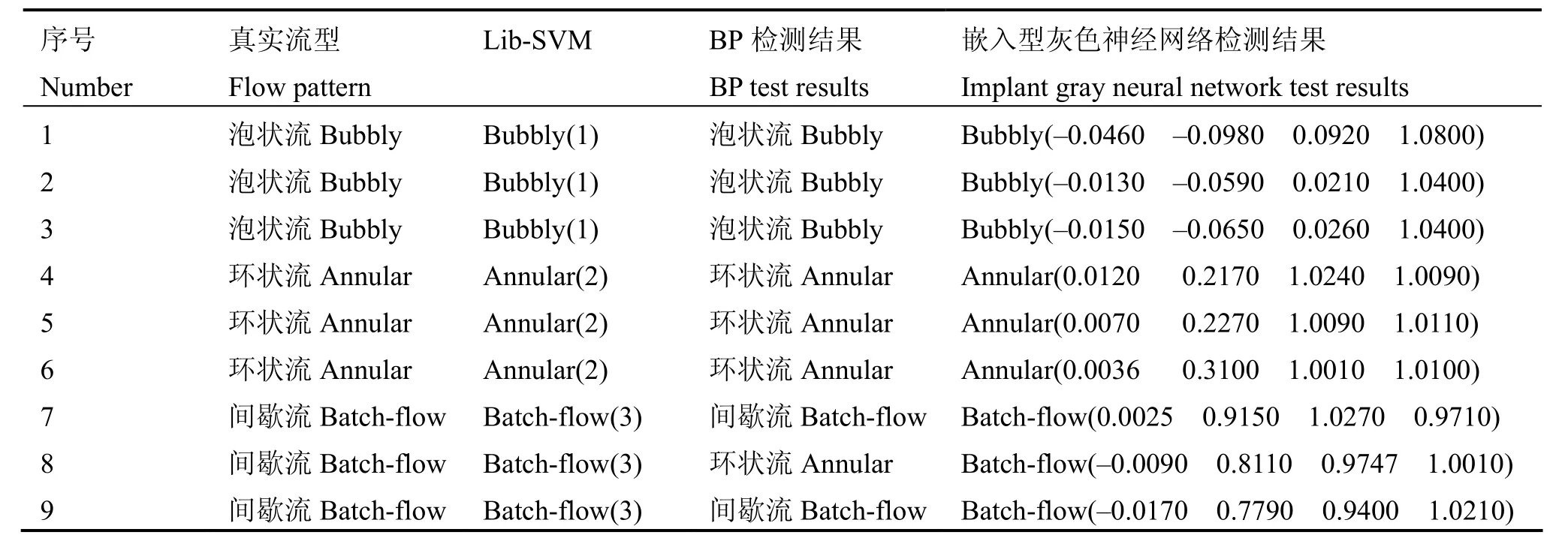
表2 三种方法预测结果对比Table 2 The comparison of the three methods.

3.3 压差信号支持向量机预测结果

将147组压差测试信号输入Lib-SVM进行预测，支持向量机对压差波动信号的检测中，对于每种流型的预测结果如表3所示。

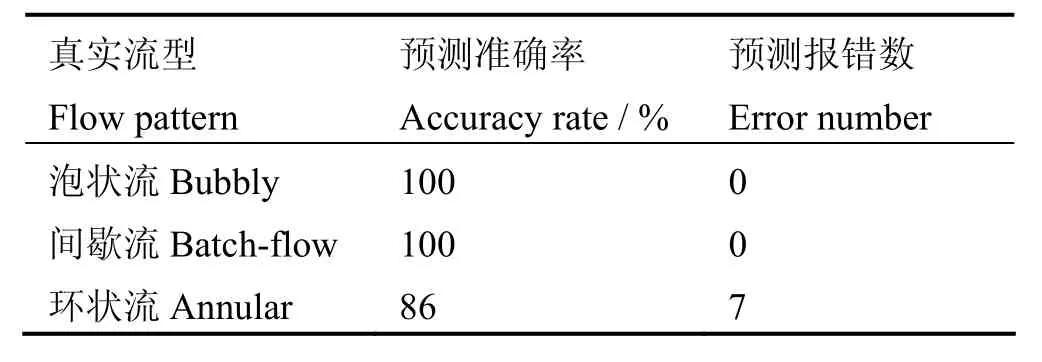
表3 Lib-SVM直接对压降信号分类结果Table 3 Lib-SVM method results.

由表3可以看出，环状流的错误预报数为7组，总的准确率达到了95.24%。Lib-SVM可以直接用于流型的压差信号辨识，其准确率较高。在流型的辨识中泡状流和间歇流都达到了较好的预测，但是环状流的预测结果仅达到86%，这可能是由于数据采集的误差等造成的。

4 结语

结合灰色系统和神经网络的优点，以嵌入型的灰色神经网络和支持向量机，分别对小波分析的气液两相流的能量信号进行分类处理，并与BP网络的结果进行对比，得出如下结论：

(1) 与传统的神经网络模型预测气液两相流流型相比，嵌入型灰色神经网络模型和支持向量机的方法预测误差更小。

(2) 嵌入型灰色神经网络模型通过对数据进行灰化处理，避免了单一模型丢失信息的缺憾，提高了模型的预测精度。

(3) Lib-SVM 对小波能量数据的分类处理方法比BP神经网络和灰色神经网络的分类结果准确。

(4) 创立了将压差信号直接输入Lib-SVM的方法，该方法可以完成流型的辨识，准确率高达95.2%，为流型的在线识别提供了依据与参考。

1 Rouhani S Z. Two-phase flow patterns: a review of research results[J]. Nuclear Energy, 1983, 11(3): 219–259

2 李菊, 董守平. 小波分析在多相流流型识别中的应用[J]. 中国石油大学学报, 2000, 24(2): 93–97

LI Ju, DONG Shouping. Application of wavelet analysis to recognition of multiphase flow pattern[J]. Journal of the University of Petroleum, 2000, 24(2): 93–97

3 黄竹青. 基于小波分析的垂直上升管气液两相流流型的识别[J]. 中国电机工程学报, 2006, 26(1): 26–29

HUANG Zhuqing. Wavelet analysis of distinguish flow pattern in vertical upward gas-liquid two-phase flow[J]. Proceedings of the Chinese Society Electrical Engineering, 2006, 26(1): 26–29

4 Nguyen V T, Euh D J, Song C H. An application of the wavelet analysis technique for the objective discrimination of two-phase flow patterns[J]. International Journal of Multiphase Flow, 2010, 36: 755–768

5 SHENG Cheng, ZHOU Tao, HONG Dexun. Research on processing of signals and images of critical heat flux in natural circulation based on wavelet transform and edge detection[C]. Applied Mechanics and Materials, 2012, (105): 2000–2004

6 张昌繁, 龚建, 刘素萍, 等. 基于不同神经网络算法的钚部件模板测量方法研究[J]. 核技术, 2012, 35(7): 525–530

ZHANG Changfan, GONG Jian, LIU Suping, et al. Template measurement for plutonium pit based on neural networks[J]. Nuclear Techniques, 2012, 35(7): 525–530

7 孙斌, 周云龙, 张玲, 等. 基于小波包分解和 Kohonen神经网络的气液两相流流型识别方法[J]. 热能动力工程, 2005, 20(1): 48–51

SUN Bin, ZHOU Yunlong, ZHANG Ling, et al. A method for identifying gas-liquid two-phase flow patterns on the basis of a wavelet packet decomposition and Kohonen neural network[J]. Journal of Engineering for Thermal Energy and Power, 2005, 20(1): 48–51

8 ZHANG Lifeng, WANG Huaxiang. Identification of oil-gas two-phase flow pattern based on SVM and electrical capacitance tomography technique[J]. Flow Measurement and Instrumentation, 2010, 21: 20–24

9 龙军, 冀海峰, 王保良, 等. 经验模态分解和小波分析在小通道气液两相流流型辨识中的应用[J]. 高校化学工程学报, 2011, 25(5): 759–764

LONG Jun, JI Haifeng, WANG Baoliang, et al. Application of empirical mode decomposition and wavelet analysis to small channel gas-liquid two-phase flow pattern identification[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(5): 759–764

10 TAN Chao, DONG Feng, WU Mengmeng. Identification of gas/liquid two-phase flow regime through ERT-based measurement and feature extraction[J]. Flow Measurement and Instrumentation, 2007, 18: 255–261

11 张毅, 杨建国. 基于灰色神经网络的机床热误差建模[J]. 上海交通大学学报, 2011, 45(11): 1581–1586

ZHANG Yi, YANG Jianguo. Grey neural network modeling for machine tool thermal error[J]. Journal of Shanghai Jiaotong University, 2011, 45(11): 1581–1586

12 周伟, 桂林, 周林. Matlab小波分析高级技术[M]. 西安:西安电子科技大学出版社, 2006

ZHOU Wei, GUI Lin, ZHOU Lin. Matlab and wavelet analysis advanced technology[M]. Xi’an: Process of Xi Dian University, 2006

13 王强, 周云龙, 程思勇, 等. 基于小波和 Elman神经网络的气液两相流流型识别方法[J]. 热能动力工程学报, 2007, 22(2): 168–171

WANG Qiang, ZHOU Yunlong, CHENG Siyong, et al. A method for discriminating gas-liquid two phase flow patterns based on wavelets and Elman neural networks[J]. Journal of Engineering for Thermal Energy and Power, 2007, 22(2): 168–171

14 顾丽莉, 石炎福, 余华瑞. 汽液两相流中压力波动信号的混沌分析[J]. 化学反应工程与工艺, 1999, 15(4): 428–432

GU Lili, SHI Yanfu, YU Huarui. Chaotic analysis of pressure fluctuation signal in the gas-liquid cocurrent flow[J]. Chemical Reaction Engineering and Technology, 1999, 15(4): 428–432