大型卧式压铸机中板的结构轻量化研究

张琦，张帅，万水平，高强，陈余秋，赵升吨

(1.西安交通大学机械工程学院，陕西西安710049;2.苏州三基铸造装备股份有限公司，江苏苏州215106)

随着制造业快速发展，合理地降低制造成本、提高产品的市场竞争力成为决定企业生存的重要因素。针对机床制造业，在竞争日益激烈的现在，如何能在保证设备强度和刚度的情况下，尽量减少材料的使用，也即是设备的结构轻量化，是当前研究的重点之一。传统的优化是在设计经验的基础上反复试验、计算和校核，其优化周期长，并且耗费大量的人力和物力。为了解决该问题，近几年出现了采用结构拓扑优化思想和有限元模拟相结合的优化方法来更科学和高效的实现结构地轻量化设计。

结构优化技术的出现最早可追溯到1904年由MICHELL 提出的桁架理论[1]，属于离散结构拓扑优化理论。1960年SCHMIT[2]将结构优化问题抽象成数学规划问题，并采用数学规划算法求解，成为结构优化领域的一个重要里程碑。连续体结构的拓扑优化设计始于1973年ROSSOW 和TAYLOR 提出的变厚度板的优化设计[3]，自1988年BENDSOE 和KIKUCHI 提出结构拓扑优化设计的均匀化方法以来[4]，连续体结构拓扑优化领域得到了迅速发展。MLEJNEK 等[5]从工程角度出发提出了结构材料密度的幂次惩罚模型，标志着拓扑优化密度法的诞生。2000年，国内学者隋允康等[6－8]提出了一种独立连续映射模型方法。目前有关拓扑优化的重要研究方向主要分为拓扑优化模型、算法的建立，去除优化中数值计算不稳定的方法及拓扑优化的应用研究[9]。

随着拓扑优化理论的发展和成熟，能够用拓扑优化解决的问题范围包括:线弹性静态结构优化问题、动力学优化问题以及非线性等复杂情况下优化问题[9]。国外CHENG 和DUYSINX 等[10－11]，国内杨德庆等[12]，研究了具有应力和位移约束下的拓扑优化问题，TENEK 和MIN 等[13－14]研究了动力学问题的拓扑优化设计，DIAZ 和TAE 等[15]研究了拓扑优化的多目标多约束问题。拓扑优化在航空、汽车领域已经开始得到了初步的应用[16]。胥志刚等[17]提出了一种基于水平集拓扑优化的车身结构轻量化研究方法。黄杰等人[18]将分布式柔性机构引入到机翼形状变化结构设计中，实现了自适应机翼表面的连续准确变化和结构轻量化。

然而，目前针对大型设备方面的拓扑优化研究还很少，特别是压铸机中的三块大板，前、中、后三板占到机器总质量的60%～70%，因此三板的轻量化设计具有重要意义。文中以压铸机中板为例，采用有限元模拟的方法，分析了中板的模架装配面不同预留厚度对优化后模型的理论减重比、变形量和应力值的影响，进而确定了最佳的预留厚度，获得了最终的优化结果。并依据最终的拓扑优化结果建立了新的压铸机中板几何及有限元分析模型，对此模型进行了静态力学分析，验证了优化结果的准确性。

1 拓扑优化理论

拓扑优化技术能在给定的设计空间内找出最佳的材料分布，拓扑的改进可大大改善结构的性能和减小结构的质量。目前连续体结构拓扑优化技术中比较成熟的是均匀化方法、变密度方法和变厚度方法。

1.1 均匀化方法

均匀化方法属于材料描述方式，引入微结构的单胞，优化过程中以微结构的单胞尺寸为拓扑设计变量，以单胞尺寸的消长实现微结构的增删，并产生由中间尺寸单胞构成的复合材料，以拓展设计空间，实现结构拓扑优化模型与尺寸优化模型的统一和连续。

该方法理论严谨、直观，设计空间完备，保证了拓扑优化最优解的存在，在早期连续体拓扑优化中起到了重要作用。但是该算法有如下缺点[19]:均匀化弹性张量的求解麻烦费时;内部微结构的形状和方向难以确定;计算结果容易产生棋盘格和多孔材料等数值计算不稳定性现象，计算结果可制造性差。

1.2 变厚度法

变厚度法属十几何描述方式，以基结构中单元厚度为拓扑设计变量，以结果中的厚度分布确定最优拓扑，是尺寸优化方法的直接推广。

变厚度法避免了均匀化方法中构造微结构的麻烦，因此可以较为方便地解决平面拓扑优化问题。但是，由于它把拓扑变量挂靠在低层次的单元厚度上，将连续体拓扑优化问题转化为广义尺寸优化问题，因此无法运用于三维结构中，应用范围较窄[20]。

1.3 变密度方法

变密度法就是引入一种假想的密度值在[0，1]之间的密度可变材料，将连续结构体离散为有限元模型后，以每个单元的密度为设计变量，将结构的拓扑优化问题转化为单元材料的最优分布问题。

用变密度法得到的拓扑优化结果是密度等值分布图，其中密度为中间值所对应的区域为假想的人工材料，在实际的工程中是没法实现的，因此在得到最优拓扑图形后要对这些区域进行人为的处理以适应实际的工程需要。基于正交各向同性材料密度幂指数形式的变密度法基于最小柔度的优化模型为[9]:

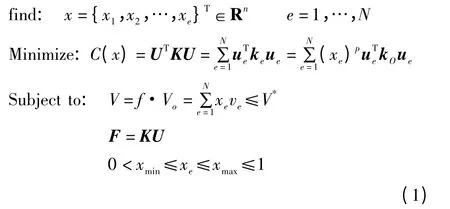
式中:xe为单元的相对密度;N为结构离散单元总数;C为结构的总体柔度;p为惩罚因子;ke为优化后单元刚度矩阵;f为优化体积比;K为优化前结构总体刚度矩阵，U 和F分别是位移列矩阵、力矢量;kO为初始单元刚度矩阵;ue为单元位移列矢量;xminxmax分别是单元相对密度的最小极限值和最大极限值;ve为优化后单元体积;Vo设计域的初始体积;V 优化后的结构体积。

在外力作用下，有限元模型应力约束的最小质量的拓扑优化公式[21]如下:

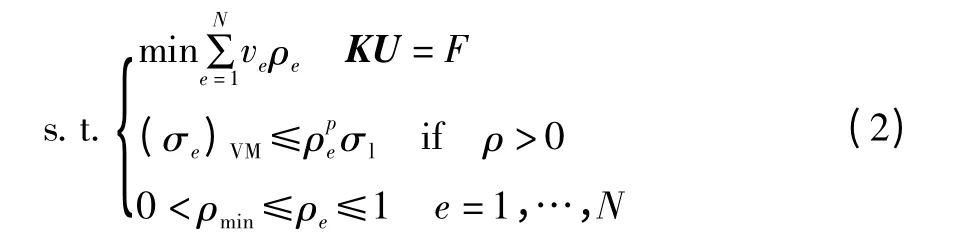
式中:ve为单元体积;ρe为单元密度;ρmin为单元最小密度;K为刚度矩阵;U为位移矩阵;F为外界载荷;(σe)VM为单元的等效V.M.应力;σl为工况l 下的应力要求;p为惩罚因子。

2 压铸机中板有限元模型的建立及参数设置

文中采用Hyperworks的Optistruct模块进行拓扑结构优化，其优化原理为变密度法。在对模型进行有限元分析前，先要建立中板的有限元模型。有限元模拟中网格的剖分质量是影响计算精度的重要因素，因此采用专业的有限元前处理软件Hypermesh 来生成高质量的网格，然后进行边界条件和相关参数的设置并进行求解。

2.1 有限元模型的建立

压铸机主要零部件的模型如图1所示，其中增力机构通过中板传力，为模具提供锁模力。压铸机中板的原始三维模型如图2(a)和(b)所示，结构比较复杂，中板模架装配面开了许多T型槽，用来固定模具，增力装配面上开了4个矩形槽，边角分布4个与格林姆柱相配合的通孔。为了获得较好的优化结果以及便于高质量网格的划分，对压铸机中板的模型做了简化，忽略了一些小的特征量，如:T型槽，倒角和圆角，如图2(c)和(d)所示。

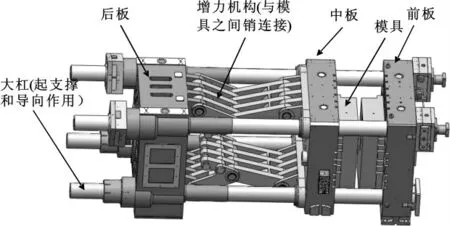
图1 压铸机部分结构示意图

对简化后的中板模型进行六面体网格划分，将模型分为设计区和非设计区两个部分，如图3中(a)、(b)、(c)所示。对两个区域的网格分布赋予同一种材料和属性，材料为球墨铸铁QT450，其弹性模量E为150 GPa，泊松比为0.25，密度为7.3×103kg/m3，其中HEX8 六面体单元为155 196个，共155 638个单元，172 978个节点。

图2 简化前、后的中板模型

图3 中板有限元模型

2.2 施加约束和载荷

在施加约束和载荷时，应尽量参考中板实际的工况和相关参数。对图1进行分析可知，中板起固定模具和传递锁模力的作用，在实际工况中可沿着格林姆柱轴向移动。因此施加载荷时，可视为销(与铰孔配合)固定，在模架面接触模具部位施加1.225×104kN的面载荷。建立约束时，边角的4个通孔内表面的六面体单元释放z 向(轴向)的自由度，约束其余自由度;约束中板底面支承座y 方向的自由度，释放其余自由度，在10个铰孔处建立10个相对应的RBE2 刚性单元，约束这些单元的全部自由度。

2.3 拓扑优化参数设置

对中板优化时，定义设计变量，即选择设计区域，定义目标函数为最小质量，定义约束条件为满足应力约束。为了便于制造加工，添加了最小尺寸、最大尺寸和拔模约束。这样优化的三大要素和制造约束都已经设置完毕，做完以上设置后提交Optistruct分析。

3 拓扑优化结果及分析

压铸机模架装配面要预留一定的厚度来装配模具，那么预留量的大小将是影响拓扑优化结果的因素之一，为了确定最佳的预留量，对以中板模架装配面的厚度为设计变量的有限元模型做了拓扑优化模拟，对比了优化后模型的减重比和中板的变形位移。对优化后的结果进行了分析，图4是取不同预留厚度的有限元模型优化后，密度值取0.3 (密度值低于0.3的单元被去除)时的结果。

图4 不同预留厚度的优化结果

可以看出:当预留厚度为25～150 mm时，设计区域的优化结果很相似，材料呈“X”型对角线分布，中间两个通孔中间部位材料较多;铰孔连接处，材料有类似筋的分布与中间相接。当预留厚度大于200 mm时，设计区域在中板中间部位的材料几乎完全被去除，铰孔处材料依然类似筋的分布和中间相接。这种材料布局符合力的传递途径，能满足应力要求。

3.1 预留厚度对优化后模型的减重比及变形量的影响

为了能直观地看出预留厚度对减重比(密度法优化前后的减重比)和变形量的影响，文中依据图4的优化结果画出了减重比和变形量随预留厚度变化而变化的趋势图(见图5)。

可直观地看出:随预留厚度的增加，优化后模型的减重比总体趋于下降。因为预留厚度越大，则代表非设计区的质量越大，设计区域的材料就越少，故优化后模型的质量越大，减重比趋于下降。

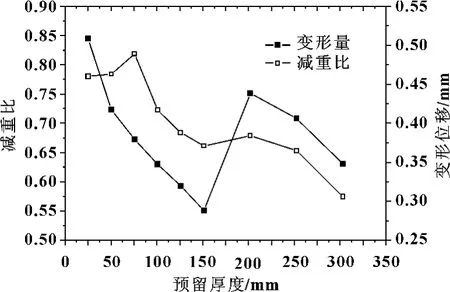
图5 不同预留厚度下的变形量和减重比

同时也可以看出:变形量总体上趋于减小。预留厚度为25～150 mm时，变形量随厚度的增加而减小;预留厚度为150～200 mm时，变形量随厚度的增加而增加;预留厚度大于200 mm时，变形量随厚度的增加而减小。因为预留量为25～150 mm时中板较薄，应力作用下变形较大，变形量随预留量的增大而减小;当预留量厚度增大到某一值(200 mm)后，中板非设计区厚度已达应力最低要求，故非设计区中间部位材料完全去除(如图4预留厚度200 mm以上图形)，优化后中板中间部位厚度比25～150 mm时的优化结果小，故变形量变大;当预留厚度继续增大，则优化后中板中间部位的厚度增加(此时预留厚度等于优化后中板中间部位厚度，如图4预留厚度200 mm以上图形)，故相同的应力下，变形量趋于减小。

3.2 优化结果的确定

通过以上分析，可知中板模架装配面预留量为150 mm时，减重比较大且变形位移较小，此时的优化结果较为合理，故确定预留量为150 mm时的拓扑优化结果为最终的优化模型。

4 中板模型重构及拓扑优化结果验证

将预留量为150 mm时的优化模型(图4(f))导出，并依据该模型在三维建模软件中重新建立新的中板几何和有限元模型(见图6)，设定好相关参数和约束及应力，对优化后中板有限元模型作静态力学分析。

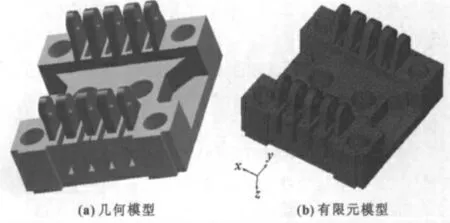
图6 优化后中板模型

对优化前、后中板的性能进行对比，结果如图7所示。

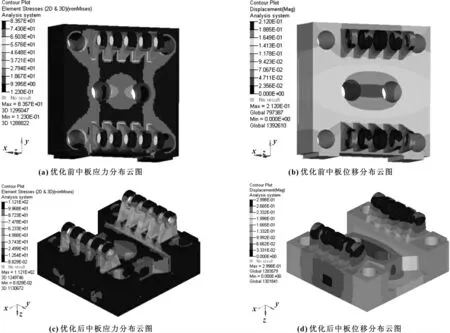
图7 优化前、后中板位移云图

优化前中板模架装配面最大位移为0.21 mm 左右，优化后为0.3 mm 左右，优化前中板最大应力为83 MPa 左右，优化后中板最大应力为110 MPa 左右。但是，优化后中板应力除铰孔边缘少数单层单元局部应力过大外(拔模、倒角、圆角后可改善)，其余部分的应力普遍在80 MPa以下，而QT450 球墨铸铁的屈服应力在310 MPa 左右，满足使用要求。通过分析对比可知，虽然优化后中板的应力和应变有所上升，但是上升幅度很小，仍然符合工况要求，而优化后材料的性能却得到了更充分的应用，中板模型质量优化后比优化前减少了26%，体现了拓扑优化的优势。

5 结束语

文中通过有限元和拓扑结构优化理论相结合的方法对压铸机中板进行了拓扑结构优化，获得的研究结论如下:

(1)当模架装配面厚度较薄时，设计区域的材料呈“X”型对角线分布;当模架装配面厚度较大时，设计区域在中板中间部位的材料几乎完全去除;铰孔处材料都有类似筋的分布和中间相接。

(2)随模架装配面预留厚度的增加，优化后模型的减重比趋于下降，而预留厚度为25～150 mm时，变形量随厚度的增加而减小;预留厚度为150～200 mm时，变形量随厚度的增加而增加;预留厚度为200～325 mm时，变形量随厚度的增加而减小。

(3)文中最终确定了模架装配面厚度为150 mm时，中板的拓扑优化结果比较理想。由中板优化后的模拟分析可知，中板的应力分布普遍在80 MPa以下，位移处于0.3 mm以下，仍符合工况要求。优化后，材料的性能得到了充分的应用，中板模型质量优化后比优化前减少了26%，体现了拓扑优化的优势。

【1】MICHELL A G M.The Limits of Economy of Materials in Frame Structures [J].Philosophical Magazine，1904，8(47):589－597.

【2】SCHMIT L A.Structural Optimization:Some Key Ideas and Insights[R].Atreke，et al.New Direction in Optimum Design.New York:Wileg，1984.

【3】ROSSOW M P，TAYLOR J E.A Finite Element Method for the Optimal Design of Variable Thickness Sheets[J].AIAA Journal，1973，11(11):1566－1569.

【4】BENDSOE M P，KIDUCHI N.Generating Optimal Topologies in Structural Design Using a Homogenization Method[J].Computer Methods in Applied Mechanics and Engineering，1988，71(2):197－224.

【5】MLEJNEK H P，SCHIRRMACHER R.An Engineering Approach to Optimal Material Distribution and Shape Finding[J].Computer Methods in Applied Mechanics and Engineering，1993，106(1/2):1－26.

【6】隋允康.建模·变换·优化:结构综合方法新进展[M].大连:大连理工大学出版社，1996.

【7】隋允康，任旭春，龙连春，等.基于ICM方法的刚架拓扑优化[J].计算力学学报，2003，6 (20):286－289.

【8】隋允康，杨德庆，王备.多工况应力和位移约束下连续体结构拓扑优化[J].力学学报，2000，32(2):171－179.

【9】左孔天.连续体结构拓扑优化理论与应用研究[D].武汉:华中科技大学，2004:5－12.

【10】CHENG G D，JIANG Z.Study on Topology Optimization with Stress Constraints [J].Eng.Opt.，1992，20(2):129－148.

【11】DUYSINX P，BENDSOE M P.Topology Optimization of Continuum Structures with Local Stress Constraints[J].International Journal For Numerical Methods In Engineering，1998，43(8):1453－1478.

【12】杨德庆，隋允康，刘正兴，等.应力和位移约束下连续体结构拓扑优化[J].应用数学和力学，2000，21(1):17－24.

【13】TENEK L H，HAGIWARA I.Static and Vibrational Shapes and Topology Optimization Using Homogenization and Mathematical Programming [J].Comp.Meth.In Appl.Meth.＆ Eng.，1993，109(1/2):143－154.

【14】MIN Seungjae，NISHIWAKI Shinji，KIKUCHI Noboru.Unified Topology Design of Static and Vibrating Structures Using Multiobjective Optimization [J].Computers and Structures，2000，75(1):93－116.

【15】DIAZ A.Sensitivity Information in Multiobjective Optimization[J].Eng.Opt.，1998，12(4):281－298.

【16】SOTO C.A.Structural Topology Optimization:From Minimizing Compliance to Maximizing Energy Absorption[J].International Journal of Vehicle Design，2001，25(1/2):142－163.

【17】胥志刚，林忠钦，来新民，等.面向车身结构轻量化设计的水平集拓扑优化[J].上海交通大学学报，2007，41(9):1393－1396.

【18】黄杰，葛文杰，杨方.实现机翼前缘形状连续变化柔性机构的拓扑忧化[J].航空学报，2007，28(4):988－992.

【19】李晶，鹿晓阳，陈世英.结构优化设计理论与方法研究进展[J].工程设计，2007，39(6):21－30.

【20】夏天翔，姚卫星.连续体结构拓扑优化方法评述[J].航空工程进展，2011，2(1):1－11.

【21】BENDSøE M P，SIGMUND O.Topology Optimization:Theory，Methods and Applications[M].Berlin:Springer-Verlag，2003.