液压电机泵中电机定子形状对电磁特性的影响

冀宏，汪翔羚

(兰州理工大学能源与动力工程学院，甘肃兰州730050)

液压电机泵是将浸油电动机和液压泵集成在一个壳体内的新型一体化电动液压动力单元，电动机和液压泵共用同一根轴，省去冷却风扇，由油流冷却，转轴无外伸轴、无需动密封，具有结构紧凑、噪声低等优点[1－2]。为了获得体积更小的电机泵，考虑缩小电机定子外形尺寸，作者设计了八边形电机。运用Ansoft RMxprt模块分析电机定子外径变化对电机性能的影响，然后采用Ansoft Maxwell 2D 对八边形电机进行空载瞬态计算和分析，最后对比分析了八边形电机与圆形电机的电磁性能。

1 八边形电机结构

作者在原液压电机泵(其结构及工作原理详见文献[1－2])圆形电机(如图1(a))的基础上对液压电机泵电机定子的外形进行了设计(见图1(b)所示)，提出了液压电机泵八边形电机结构。由图1可知，八边形电机定子外形尺寸较圆形电机有所减小，其转子和泵芯部分没有改变。

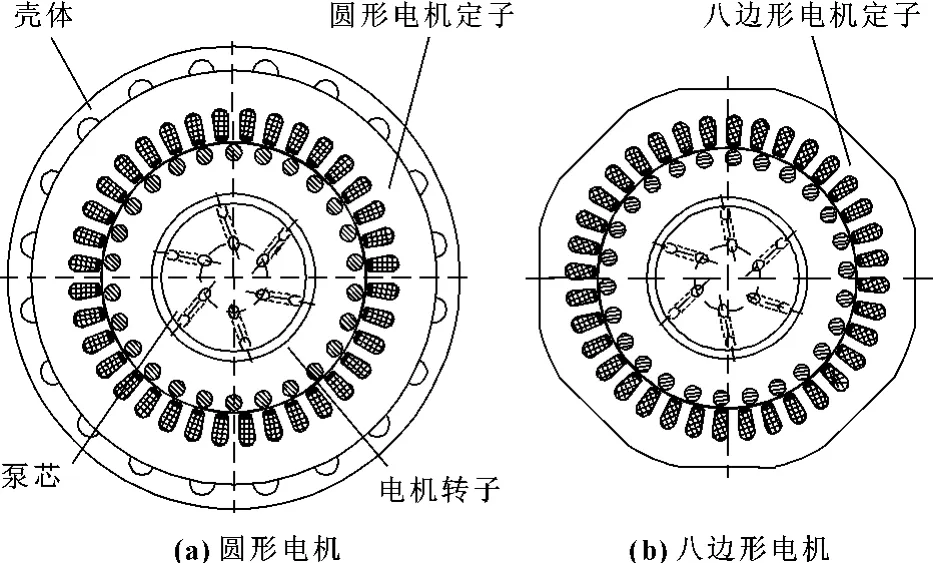
图1 电机泵剖面图

液压电机泵圆形电机的主要参数见表1。为了分析电机定子外径变化对电机性能的影响，在前处理RMxprt模块中调整液压电机泵圆形电机外径尺寸，将原来的定子外径改为参数L1，L1的取值范围为250～260 mm，每1 mm为一个计算步长，进行数值计算，得到电机性能参数随定子外径的变化，如表2所示。

表1 液压电机叶片泵电机的主要技术参数

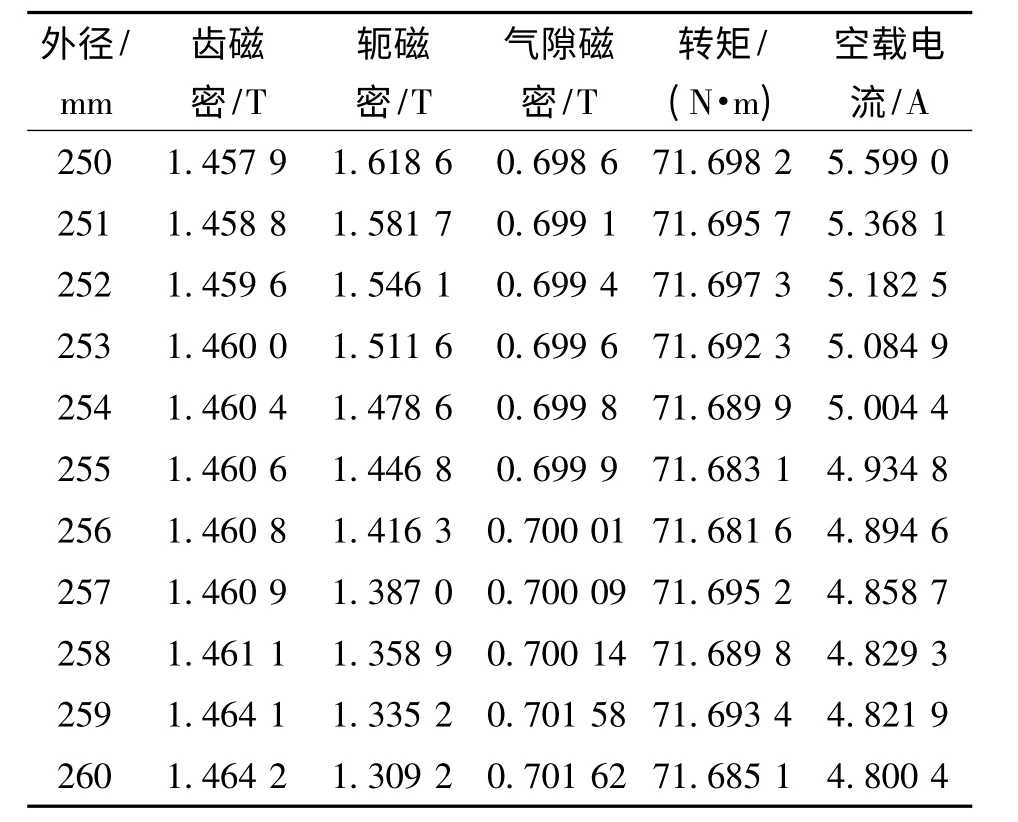
表2 液压电机泵电机随定子外径变化的性能参数

表2列出了电机定子外径变化时，定子轭部磁密、定子齿部磁密、气隙磁密、转矩及空载电流随电机定子外径的变化数据。为了保证电机合理的铁心损耗和空载电流，定子轭部磁通密度一般低于定子齿部磁通密度[3]。由表2可以看出，液压电机泵电机定子外径取值范围在255～260 mm之间时，定子轭部磁密小于定子齿部磁密。

取电机定子外径为255 mm，并切掉八个边以提供一定的通流面积，作为电机泵冷却流道，设计出八边形电机。经计算，设计出的八边形电机定子比原液压电机泵中圆形电机定子的体积减小16% (如图1所示)。

2 圆形电机与八边形电机电磁性能比较

2.1 电机模型的建立

采用Ansoft Maxwell 2D软件分别建立圆形电机和八边形电机的二维有限元模型。现假设如下:因为电源的频率很低，位移电流可以忽略;不考虑端部效应;忽略定子铁心外表面和转子铁心内表面的漏磁;电磁场的各场量随时间按正弦规律变化[4]。

(1)构建模型

在项目管理器中建立电机有限元分析项目，采用瞬态求解器Transient。建立xy 平面几何模型。电机电磁场有限元模型如图2所示。

图2 电机泵定转子部分几何模型

(2)定义材料属性

指定模型所用的材料:电机定子铁心与转子铁心材料为D23，线圈指定为Copper，转子导条材料指定为Copper_75C。指定Inner_region、Out_region、Air_gap以及Band为Oil Hydraulic。由于液压电机泵电机是全部浸在液压油中的，材料库中并无此种材料，需要将材料特性输入到电机材料数据库中。其中液压油相对磁导率μr(MURX)=1[5]，密度取为850 kg/m3。

(3)网格剖分与求解设置

设置定子外径的边界矢势为0，添加三相电压激励源。设置运动选项，并考虑电机空载启动过程。对模型进行剖分，采用Inside Selection 命令对电机整体进行内部剖分，并使用Surface Approximation 命令对边界曲线的部位进行进一步的细致剖分。为使计算精确，在气隙部分剖分较密，网格剖分如图3所示。

图3 电机网格划分

设置硅钢片铁损系数，并选择求解参数——定子的铁心损耗(Core Loss)。在求解参数的设置中设置步长为0.001 s，计算时间为0.4 s。设置模型长度为155 mm。

2.2 仿真结果分析

针对八边形电机空载启动进行分析。当电机空启动至稳定运行时，电机励磁电流If=4.93 A，转速n=1 450 r/min。

由图4可见:当八边形电机运行时，电磁转矩在启动过程中波动明显，由于液压油的负载效应[6]，使得电机的启动转矩增大。电磁转矩大幅波动的过程中，电机转速快速增加，在t=0.3 s 附近趋于稳定。由图5可见:在电机空载启动过程中，三相电流波动幅值很大，这种冲击电流对电机运行的稳定性有很大影响，在t=0.2 s 附近，三相电流对称分布，且基本接近正弦。图6为电机空载启动时转速随时间的变化曲线图，其中从启动到t=0.22 s 转速变化较大，t=0.22 s以后转速变化平缓，逐步达到同步转速1 500 r/min。图7所示为电机空载启动时电机笼型绕组中的感应电流在电机启动过程中感生出较大的电流，从而产生较大的电磁转矩。转子导条的电流与启动时电机负载大小有关，当电机里充满液压油时，电机启动相当于增加了负载[7]。最后随着转子转速的提高，转子笼型绕组切割磁场的频率增加，感应电流减小，当电机转速为1 450 r/min时，转子笼型绕组电流接近0。大约t=0.3 s时，电机工作稳定处于空载状态。

图4 空载启动时电磁转矩曲线

图5 空载启动时三相绕组电流曲线

图6 空载启动时转速曲线

图7 空载启动时的转子电流曲线

2.3 圆形电机与八边形电机电磁场比较

对于圆形电机和八边形电机，由于定子外形尺寸不同，首先考察不同模型定子轭部磁密及齿部磁密的大小。图8是t=0.3 s时的电机定子轭部磁密在轭部中心圆(轭部平均直径)上磁感应强度模的曲线。可以看出，八边形电机的轭部磁密大于圆形电机轭部磁密。在轭部中心圆上，圆形电机最大轭部磁密为1.350 1 T，平均轭部磁密为0.874 7 T;八边形最大轭部磁密为1.637 1 T，平均轭部磁密为1.072 1 T。分析其主要原因，是由于磁束闭环上各部分的有效宽度决定其通过的磁通密度，八边形电机定子轭部铁心截面减小，其有效轭部磁路宽度减小，在磁通量不变的前提下，八边形电机的轭部磁密较大。

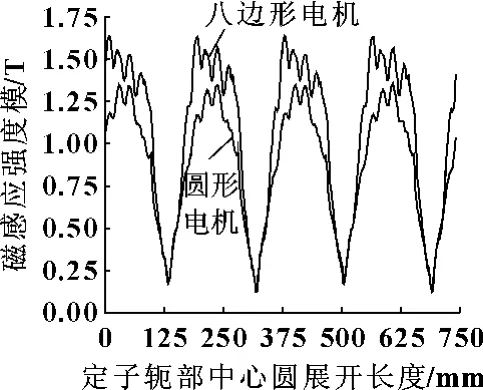
图8 定子轭部中心圆上磁感应强度模的曲线

图9是t=0.3 s时的电机定子齿部磁密在齿部中心半圆(半圆位于定子齿一半高度处)上磁感应强度模的曲线。可以看出:与轭部磁密相比，齿部磁密变化比较小，在同样的三相电压激励源条件下，圆形电机齿部最大磁密为1.606 1 T，八边形电机齿部最大磁密为1.562 3 T，两者相差较小。这主要是由于圆形电机与八边形电机的不同之处在于轭部铁心截面的变化，对轭部磁密影响较大，而对齿部磁密影响较小。最后校验定子齿最小截面处的齿磁密，不应该超过2 T。当t=0.3 s时圆形电机定子齿部最小截面处的平均齿磁密为1.225 5 T，八边形电机定子最小截面处的平均齿磁密为1.287 0 T，其值都未超过2 T，说明八边形电机设计合理。

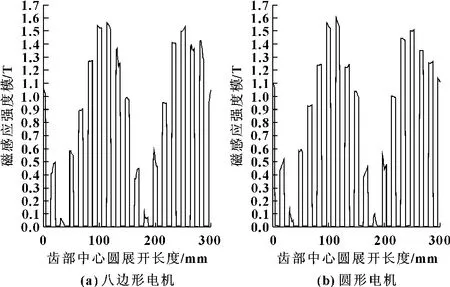
图9 定子齿部中心半圆上磁感应强度模的曲线

图10为电机空载运行0.3 s时的磁通密度分布图。可知:八边形电机和圆形电机磁密分布相似，且磁密较大的部分主要出现在一相的定子绕组、转子绕组之间(大小见图10所示)。八边形电机定子轭部四极对称部位磁密较大，定子轭部最高磁密为1.946 4 T，圆形电机定子轭部最高磁密为1.558 3 T，可见八边形电机轭部磁密较圆形电机轭部磁密局部有所变大。

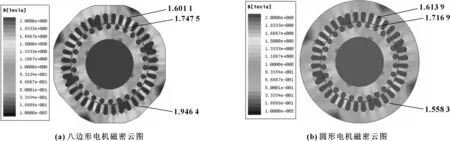
图10 磁通密度云图

为了更好地分析磁通密度的分布，在Ansoft 后处理中，利用场计算器绘制出t=0.3 s时八边形电机与圆形电机气隙中心磁通密度变化曲线，如图11所示。理想的气隙磁密随圆周长度的变化曲线应该是正弦曲线，且呈现周期性变化趋势。由图11可知，八边形电机和圆形电机在不同程度上都存在谐波分量，且变化趋势与普通空冷电机相同。谐波磁势会对电机泵带来一系列不利的影响，如产生较大的损耗而使电机的效率降低和温升增高，产生较大的振动、噪声和附加转矩，影响电机启动等[8]。利用FFT函数对曲线进行傅里叶变换，频谱图如图12所示。圆形电机的基波幅值为0.757 37，较大幅值的谐波为0.178 5，占基波幅值的23.57%;八边形电机的基波幅值为0.757 14，较大幅值的谐波为0.176 73，占基波幅值的23.34%。其余谐波幅值较小，在此忽略不计。可见，八边形电机谐波分量较小，因此造成的影响较小。

图11 空载气隙磁通密度沿圆周方向变化曲线

图12 气隙磁通密度傅里叶分析

3 总结

利用Ansoft软件对液压电机泵中圆形电机与八边形电机空载稳定运行时的电磁场进行分析与计算，得到如下结论:

(1)所设计的八边形电机电磁性能合理，其定子体积较圆形电机定子体积减小16%，八边形电机定子轭部磁密有所增加，磁密最大值为1.946 4 T。相比圆形电机，八边形电机气隙谐波分量影响较小。

(2)八边形电机是依据普通空冷电机要求进行设计的。在液压油冷却情况下，电机的冷却效果更好，考虑在此基础上对样机进行结构优化设计，能进一步缩小电机尺寸。

【1】冀宏，张立升，王峥嵘，等.电动液压动力单元的一体化演变[J].机床与液压，2011，39(19):117－120.

【2】冀宏，丁大力，王峥嵘，等.液压电机泵内置孔板离心泵的流场解析与优化[J].机械工程学报，2009，45(6):199－205.

【3】陈世坤.电机设计[M].2版.北京:机械工业出版社，2000.

【4】赵博，张洪亮.Ansoft12 在工程电磁场中的应用[M].北京:中国水利水电出版社，2010.

【5】张大杰，高殿荣，王有杰，等.基于ANSYS的轴向柱塞液压电机泵电磁场数值计算与分析[J].机械工程学报，2008，44(12):69－74.

【6】冀宏，孙磊，王峥嵘，等.液压电机泵浸油电机的负载效应[J].兰州理工大学学报，2009，35(4):52－56.

【7】祁琪，冀宏.基于Ansoft的液压电机泵电机的仿真研究[J].机床与液压，2010，38(17):102－105.

【8】高殿荣，张大杰，温茂森，等.永磁同步驱动轴向柱塞液压电机泵电磁场研究[J].机床与液压，2011，39(3):5－9，32.