基于CFD的伺服阀衔铁组件啸叫分析
陈元章
(南京机电液压工程研究中心航空机电系统综合航空科技重点实验室,江苏南京210061)
电液伺服阀因其控制精度高、响应速度快而最初应用于航空航天领域,随着液压伺服技术的发展,电液伺服阀的应用已经扩展到冶金、化工、机械制造、地质勘探、工程机械等需要精确控制的领域。电液伺服阀作为液压伺服系统中的关键部件,它把机械、电子和液压技术紧密结合在一起,其性能直接影响到整个液压伺服系统的性能,而衔铁组件又是电液伺服阀的核心部件,通过它才能把控制信号的典型号与系统的机械系统、流体系统串联起来,所以其性能直接影响了整个伺服阀的性能。但在实际的使用中,偶尔会发生伺服阀啸叫现象,从而使伺服阀性能改变,系统性能降低,甚至会发生伺服阀衔铁组件破裂漏油、系统失控的故障。
所以,研究伺服阀弹簧管啸叫问题就显得尤为重要,但由于伺服阀啸叫的偶发性和随机性,伺服阀的啸叫很难复现。并且伺服阀啸叫不仅仅是伺服阀本身的问题,它往往跟系统的结构、使用工况、工作环境等因素相关联,所以很多时候是系统发生了伺服阀啸叫问题,但在生产厂家的试验室根本不能复现,这就进一步增加了伺服阀啸叫机制分析的难度,所以从实验流体力学上很难进行伺服阀啸叫的机制分析。同时,由于伺服阀内部油路的复杂性,仅仅从理论流体力学等进行理论上的分析难度更大。近年来,随着高速数字计算机的发展,以及为使用计算机解决物理问题而发展起来的精确算法,一门介于实验流体力学和理论流体力学之间的计算流体力学 (Computational Fluent Dynamics,CFD)得到了长足发展,它既克服了理论流体力学问题中诸如非线性等一系列复杂问题的理论解计算问题,又克服了实验流体力学中模型尺寸、流场扰动、人为因素和测量精度的限制。所以,计算流体力学已经成为流体力学研究中的第3种方法,目前在分析和解决流体力学问题的时候,计算流体力学已经成为与理论和实验平等的角色,CFD方法与传统的理论分析方法、实验量测方法组成了研究流体流动的完整体系。
作者基于CFD技术,就某型伺服阀在研制过程中发生的弹簧管批次性啸叫问题进行分析,并利用CFD技术提出相应的解决方法。
1 试验过程
文中提及的衔铁组件结构见图1,图中衔铁起伺服阀驱动控制作用,弹簧管起弹性支撑并隔离流体和电信号作用,偏转板起分配液流作用。弹簧管是弹性元件,在微小的电信号作用下需要发生弯曲变形,所以壁厚一般只有0.06~0.09 mm,因而其刚度不能太大。因此,弹簧管既是伺服阀衔铁组件中的关键部件,也是其中的薄弱环节,伺服阀啸叫很多时候就是由弹簧管的振动引起的,而且,因为弹簧管的壁厚相当薄,在振动啸叫的时候,弹簧管往往会发生破裂。
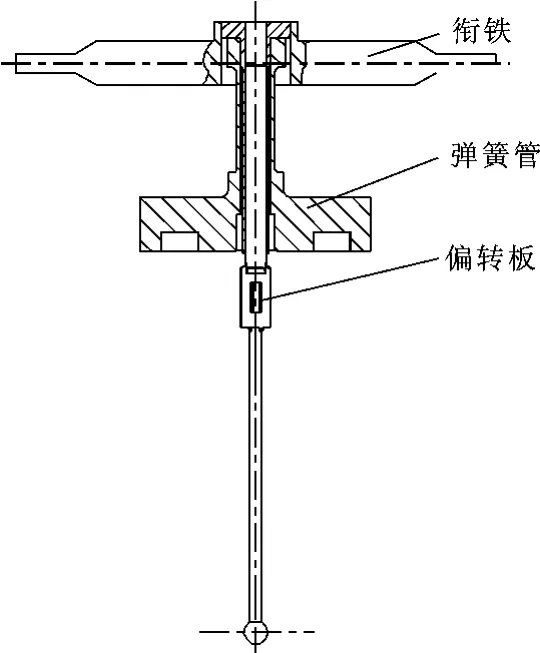
图1 衔铁组件结构图
把衔铁组件安装在如图2所示的实验夹具上,在图示A-A的位置处做剖面,剖面结构见图3。流体从射流片的入射口流入,通过偏转板中间的缝隙进入到射流片的两个接收口。
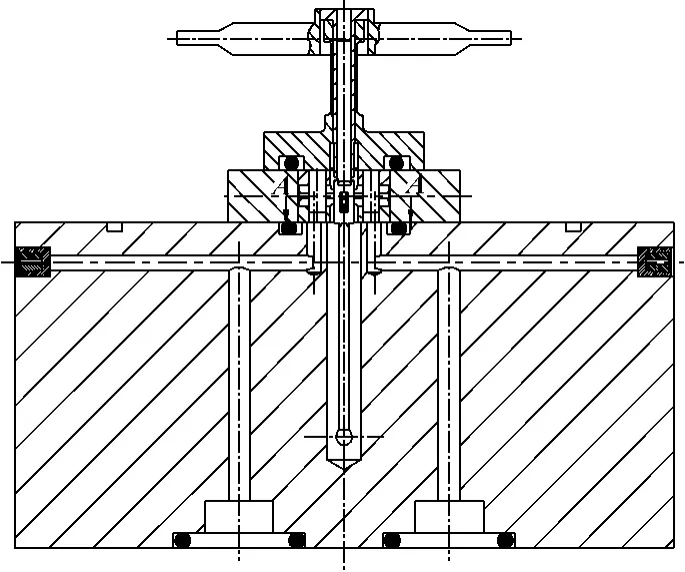
图2 衔铁组件实验安装图
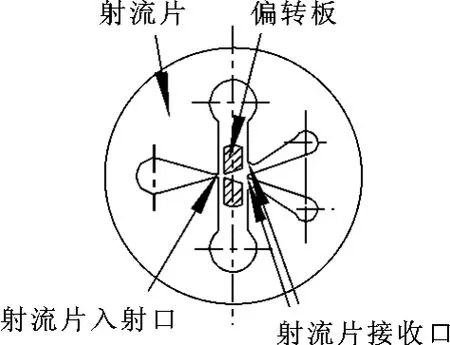
图3 射流结构剖面图
把图2所示的试验夹具和衔铁组件试验件安装在试验台上,试验台使用的工作液为12号航空液压油,试验进油压力为21 MPa,回油压力约为0。试验中,在把试验台进油压力升到21 MPa的时候,衔铁组件发出刺耳的啸叫声,触摸衔铁组件能感到明显的高频振荡,更换试验件,更换的5个衔铁组件均发生了高频振荡啸叫。
针对该现象进行分析。
2 CFD 模拟求解
试验中的衔铁组件在流体作用下产生的振动啸叫,属于典型的流致振动问题,流致振动基本方程可用如下算子形式来描述:

式中:x(X,t)为响应矢量;
X、t分别是空间、时间变量;
f(X,t)为激励矢量,通过求解流场方程来获得。
在动力学及有限元中的形式为:

由于结构的运动会影响流场从而改变流场对结构的作用力,所以,式 (1)是非线性体系,不易求解,因此,将式(1)右端分解为:
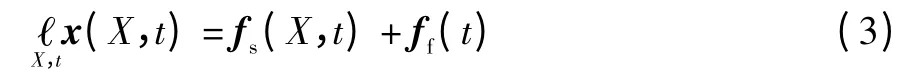
式中:fs(X,t)是非线性项,与结构运动有关,称为运动相关的流体力;
ff(t)与结构的运动无关,仅与流体运动有关,称为流体激振力。
试验中作为结构部件的衔铁组件本身是静止部件,不会因为自身的机械运动而产生振动激励,所以式(3)中的非线性项fs(X,t)可以忽略,仅考虑流体激振力ff(t)的作用。
流体激振力ff(t)可以通过CFD 计算流场的压力获得。文中即使用Fluent软件包的前处理软件Gambit进行网格划分,再把划分好的网格导入Fluent 求解器进行求解。
把图3所示的结构图抽取成Gambit 和Fluent模型,见图4。因为抽取的模型为对称结构,所以为减少计算量、加快计算效率,取一半的结构进行网格划分,如图5。利用Gambit 划分网格,因为阀口存在明显的锐边,对阀口进行网格细化,划分网格详见图6,共计79 924个网格(图6为计算结束后在Fluent中取的整体视图)。
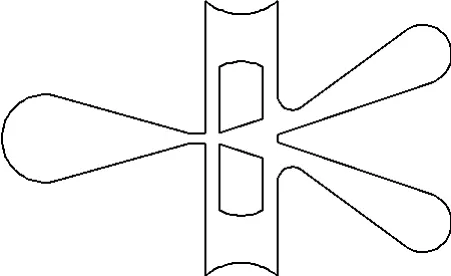
图4 液压放大器模型
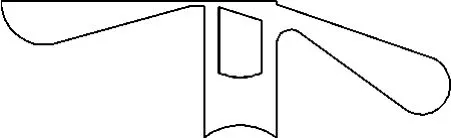
图5 简化后的液压放大器模型

图6 划分的网格图
把划分好网格导入Fluent 进行计算,在数值求解的过程中,首先进行以下的设定:
(1)流体介质是液压油。因为Fluent 中没有适合的流体,所以按12号航空液压油的属性定义材料的特性:
ρ=850 kg/m3。
ν=0.010 2 kg/(m·s)。
(2)流体为牛顿流体。
(3)流体流态。由雷诺方程得:

所以,流体流态为湍流,选取Fluent模型为标准型k-ε模型。
(4)数值计算方法采用有限体积法中常用的SIMPLE (Semi-Implicit Method for Pressure-Linked Equations)算法求解离散方程组。
(5)为保证计算精度,选取二阶模型。
设定后对模型进行求解计算,计算结果见图7—11。
图7为流体的压力云图,可以看出偏转板前后有一定的压差,选取偏转板左侧的区域可得此区域的压力为25.50~29.01 MPa,选取偏转板右侧的区域可得此区域的压力为18.49~22.00 MPa。
图8为流体的速度云图,图9为速度矢量图,可以看出偏转板出口与射流片结合处存在明显的涡流涡旋。图10为速度矢量图的局部放大图,更能清晰地看到涡旋的形式和方向。
图11为流体沿轴线方向的压力曲线图,从图中所做的辅佐线可以看出从-0.000 25~0.000 5 m的位移范围内,即从偏转板入口处到射流片接收口处,压力从2.13×107Pa 急剧上升到3.0×107Pa。

图7 压力云图

图8 速度云图

图9 速度矢量图

图10 局部的速度矢量图

图11 沿轴线方向的压力曲线图
从图7—11可以看出:这种结构下的模型在偏转板出口处和射流片接收口处存在明显的卡门涡,偏转板内的抹茶切应力和漩涡运动消耗了大量能量,使尾流区的压强降低,使偏转板左右两侧的压差变大,形成压差阻力,且此卡门涡产生一定的流体激振力,偏转板在此激振力的作用下产生了受迫振动,因为起弹性扰动的弹簧管弹性模量低、刚度小,从而带动整个衔铁组件做高频振荡,产生啸叫。衔铁组件的高频振荡又会影响油路内部流场的重新分布,流体流动与偏转板和射流片之间构成一种强烈的流固耦合关系,从而加剧了流体的压力脉动,使衔铁组件的振动进一步加剧。

图12 液压放大器模型
为验证以上分析,改变偏转板的结构重新进行模拟计算和实际测试。改变后的结构剖面见图12,对其重新进行网格的划分,共计80 546个网格,详见图13。

图13 划分的网格图
把划分好的网格导入Fluent 进行计算,计算结果见图14—17。

图14 压力云图

图15 速度云图

图16 速度矢量图
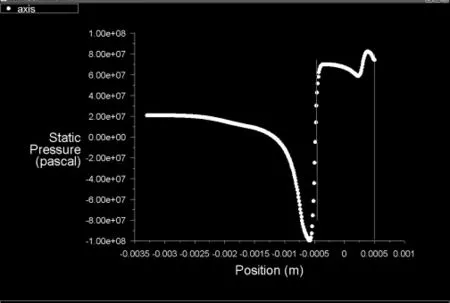
图17 沿轴线方向的压力曲线图
图14为流态的压力云图,图15为速度云图,图16为速度矢量图,图17为沿对称轴方向的压力变化图。可以看出:产生的涡流涡旋消失,且偏转板左右两侧的压力基本相等;从对称轴方向的压力变化图中也可以看出:在-0.000 4~0.000 5 m 内,即在射流片进出口之间的压力波动很小。
把更改结构的试验件安装在试验台上进行测试,5件衔铁组件试验件均未产生振动啸叫,并且在整个伺服阀的安装调试试验过程中也未出现伺服阀高频啸叫现象。
3 结论
(1)文中所做的实验模拟再现了伺服阀弹簧管啸叫现象,为理论分析提供了实验基础;
(2)通过Gambit、Fluent 等软件模拟了伺服阀衔铁组件流场的流固耦合现象,发现伺服阀衔铁组件发生高频啸叫时,衔铁组件内部流态产生了卡门涡,并伴随着很大的压差阻力和流体激振;
(3)通过改变产品的内部结构,再次进行流体流态的CFD 模拟,消除了衔铁组件内部流态的卡门涡,并在实际的产品试验中消除了伺服阀弹簧管啸叫现象。
(4)文中只是定性分析了伺服阀衔铁组件啸叫的原因,并未定量分析伺服阀衔铁组件啸叫的原因。并不是流体中一旦产生涡流涡旋就会引起伺服阀的啸叫,只有当产生的流体激振力达到一定的数量级,克服衔铁组件的综合刚度,从而迫使伺服阀衔铁组件做受迫运动;或者当流体的卡曼涡旋脱落频率与伺服阀衔铁组件在流体中的固有频率接近,引起伺服阀衔铁组件共振的时候,伺服阀衔铁组件才会产生振动,甚至产生啸叫。清华大学的陈佐一教授更是开宗明义地提出:任何一种工程构件,在外界各种干扰的影响下,总会存在各种微小的振动,即使对于定常来流,这种微小振动也会使流经振动物体的流场产生振荡,而振荡流又进一步作用于振动物体。所以,自激振动的稳定性取决于物体振动过程中振荡流场与物体之间能量交换的性质。在振动过程中,振荡流场对振动物体做正功,则使振动加剧而导致不稳定;否则流体起了阻尼作用,振动是稳定的。这也是下一步需要继续研究的方向。
(5)虽然产品内部流态产生卡门涡未必一定会引起伺服阀的振动啸叫,但尾涡的存在毕竟增大了伺服阀啸叫的隐患。相关文献指出:涡旋脱落时候产生的振动影响比尾涡本身的影响更大。当结构件运动时,式(3)中的运动相关的流体力fs(X,t)不能再忽略,非线性项fs(X,t)的存在会引起涡的脱落频率和分离特性、激振力的大小和相位、近尾迹的结构和湍流场,甚至对远尾迹带来影响,使产品内部流场更加复杂,振动啸叫产生的可能性更大。而且,在伺服阀的实际使用中,伺服阀使用单位为了提高伺服阀的灵敏度经常会对伺服阀施加几百赫兹频率的激励,使伺服阀衔铁组件处于一定频率的振动,更激化了伺服阀啸叫的可能性。在伺服阀使用工作环境恶劣的时候,如飞机发动机开车,飞机、导弹在空中飞行的时候,伺服阀啸叫的隐患就更为突出。
(6)传统的机械设计只能从理论和经验上尽量避免引起伺服阀振动啸叫结构的存在,但是很难从实际上避免。作者利用CFD技术提供了一种避免伺服阀振动啸叫的方法,降低了产生伺服阀啸叫的可能性。
【1】梅里特H E.液压控制系统[M].陈燕庆,译.北京:科学出版社,1976.
【2】田源道.电液伺服阀技术[M].北京:航空工业出版社,2008.
【3】ANDERSON John D.计算流体力学基础及其应用[M].吴颂平,刘赵淼,译.北京:机械工业出版社,2007.
【4】陈佐一.流体激励[M].北京:清华大学出版社,1998.
【5】王福军.计算流体动力力学分析[M].北京:清华大学出版,2004.
【6】周俊杰,徐国权,张华俊.Fluent 工程技术与实例分析[M].北京:中国水利水电出版社,2010.
【7】雷天觉.液压工程手册[M].北京:机械工业出版社,1991.
【8】刘明侯,ZHOU Y,陈义良,等.结构振动对湍流近尾迹的影响[J].力学学报,2001,33(2):163-172.
【9】席志德,陈炳德,李鹏洲.弱耦合体系流致振动计算方法[J].原子能科学技术,2008,42(S2):444-447.
【10】毛庆,姜乃斌.孔板诱发管道流致振动响应的计算方法[J].核动力工程,2009,30(3):22-26.

