广义模糊时间序列模型模糊区间划分研究

邱望仁，刘晓东，贺建军

（1.景德镇陶瓷学院 信息工程学院，江西 景德镇 333403；2.大连理工大学 控制科学与工程学院，辽宁 大连 116024；3.大连民族学院 信息与通信工程学院，辽宁 大连 116602）

0 引 言

自从1993年Song等提出了模糊时间序列预测模型［1－2］以来，人们对这种模型进行了深入广泛的研究.应用方面，它已经被应用于招生人数［1－6］、股指［7－11］、温度［12］、外汇交易［13］、文化卫生［14－15］等各个领域的预测工作中.理论方面，对模型中模糊关系的建立与利用［3－4，9，11］、模糊规则的挖掘［10］等方面有了大量的研究成果.

然而，不同领域问题千差万别，即使在同一领域，面对的是同一问题，由于看待问题的角度、处理问题的方式均可能不同，则对待它的态度也不一定相同.故人们对模糊时间序列模型的研究工作远没结束.传统模型只考虑观测值对应的隶属度最大的模糊子集，它在哲学上可以理解为抓主要矛盾.然而，据辩证法的思想，次要矛盾在一定的条件下也可能转变为主要矛盾，这要求人们在处理问题时要考虑次要矛盾的影响.该思想在模糊时间序列模型中体现为在预测过程中要考虑观测值的模糊子集某一个适当的子集对预测结果的影响，从而得到合理、可靠的结果.基于这种考虑，文献［9］提出了广义模糊时间序列模型.

由于广义模型提出的时间较短，对它的研究还有待于深入.根据人们对传统模型的研究得知，模糊区间的划分对模型的预测效果有很大的影响，所以本文以3种不同模糊区间的划分方法为基础，建立广义模糊时间序列模型，并对模型的预测结果进行分析.

1 广义模糊时间序列模型的框架

下面在传统模糊时间序列模型的框架下，介绍几个必要的定义和广义模糊时间序列模型.

1.1 模糊时间序列模型的相关定义

定义1 设U为论域，用区间表示为［a，b］，给定U的一个次序分割集为U＝｛u1，u2，…，un｝，定义A为论域U上的语义变量集（即模糊集），并记为

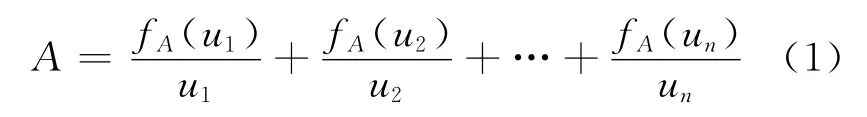
式中：fA是定义在A上的模糊隶属函数，fA：U→［0，1］；fA（ui）表示ui在模糊集A上的模糊隶属度的值，1≤i≤n.

在模糊时间序列模型中，常用如下三角函数来定义模糊集：

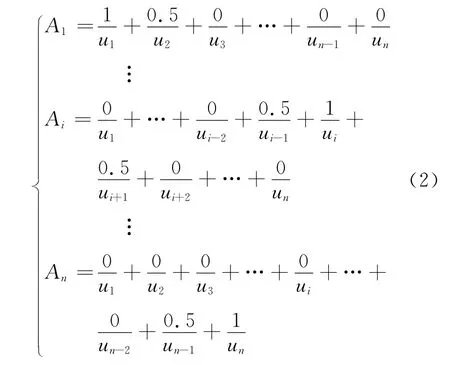
对模糊概念Ai的隶属度函数常用下式来计算：

其中lin表示子区间的长度，t为时刻.

定义2 对任意一个固定的Y（t）（t＝…，0，1，2，…），设Y（t）R，即为实数域的子集，Y（t）上定义了一组模糊集fi（t）（i＝1，2，…），且F（t）＝｛f1（t），f2（t），…｝，则称F（t）为定义在Y（t）上的模糊时间序列.

这里的F（t）为语言变量，fi（t）为F（t）中可能的语言值（即定义1中的fA（ui））.设它有n个模糊子集，经典模糊时间序列模型的相关定义可以作如下推广.

定义3 设（μ1（t），μ2（t），…，μn（t））、（μ1（t＋1），μ2（t＋1），…，μn（t＋1））分别为t和t＋1时刻的观测值F（t）、F（t＋1）在给定模糊子集上的隶属度.μi（t）和μj（t＋1）分别对应着模糊集Ati和At＋1j，则在相邻两个观测点可以得到n2个逻辑关系，它们可以表示为Ati→At＋1j（i，j＝1，2，…，n），称这些关系为广义模糊逻辑关系.这里的Ati也被称为模糊关系的左件（或者前件），At＋1j被称为模糊关系的右件（或者后件）.

这个定义包括观测值的模糊集构成的全部模糊关系，而传统定义中只考虑观测值中隶属度最大值模糊集生成的模糊关系.

定义4 设（μ1（t），μ2（t），…，μn（t））、（μ1（t＋1），μ2（t＋1），…，μn（t＋1））分别为t和t＋1时刻的观测值F（t）、F（t＋1）在给定模糊子集上的隶属度.μi（t＋1）和μj（t＋1）分别对应着模糊集Ati和Atj＋1.如果（t）是（μ1（t），μ2（t），…，μn（t））的最大值（t）是（μ1（t＋1），μ2（t＋1），…，μn（t＋1））的最大值，则称为第一主要模糊关系，其中对应的模糊集.当（t）是（μ1（t），μ2（t），…，μn（t））的第k大值时，称为第k主要模糊关系.

根据该定义，第k主要模糊关系记为GL（1，k）.这里1是指两样本之间只隔一个时间段，对于隔多个时间段的关系则是高阶模型研究的内容.因此该定义中的两类模糊关系可以分别记为GL（1，1）和GL（1，k）.由于人们在分析问题时次要矛盾不会考虑太多，k在实际应用中的取值一般比较小.

1.2 不同层次模糊逻辑关系的融合

根据定义4，模型的模糊关系非常多，且不是同一层次的，在理论上需要一个运算将不是同一层次但又都包含对决策有影响的信息的关系综合起来.因此，下面给出一个初步的运算，为建立模型作准备.

定义5 设A（j）tj为第j个主模糊逻辑关系（即GL（1，j））中的前件，R（j）（tj，i）是根据训练集得到的模糊逻辑关系矩阵中逻辑关系Atj→Ai的个数.则定义∧k为综合各层次模糊关系矩阵信息的运算：

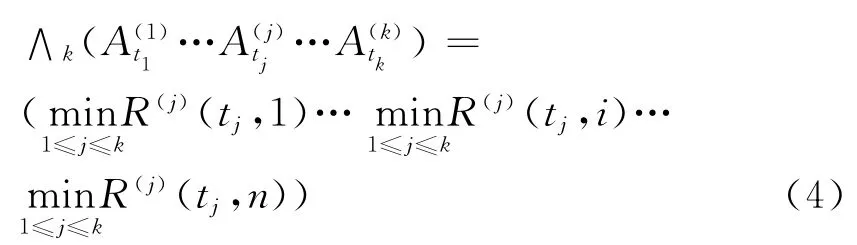
详细的计算过程可参见文献［9］.本文模型即采用该运算进行信息综合而得到的预测结果.

1.3 广义模糊时间序列模型的建立步骤

下面将参考传统模型，以上述5个定义为基础，介绍建立广义模糊时间序列模型的过程.

步骤1 对论域进行模糊划分.

这一步和传统模型一样，要做的工作就是确定论域和各模糊子集的划分.本文中的模糊集和模糊隶属度函数分别选用式（2）和（3）.

步骤2 建立模糊关系集合和模糊关系矩阵.

利用式（3），求样本数据对每个模糊集的隶属度，从而确定相应的模糊概念.这一步要根据k的取值情况，记录与每个观测数据相对应的模糊集，然后再根据定义4确定相邻两样本的广义模糊逻辑关系.这里可以得到k类模糊关系集合，它们分别是GL（1，1），…，GL（1，k）层次下的模糊关系.最后，根据步骤2得到的全体广义模糊逻辑关系，按模糊关系矩阵的建立方法得到模糊关系矩阵.

步骤3 求出观测值对给定的模糊集的隶属度值.

先对观测样本利用式（3）求出它对各模糊集的隶属度，根据k的取值确定各层次下的样本在模糊关系矩阵中预测下一时刻数据的依据.这里要注意的是GL（1，k）层次下模糊关系矩阵中要选取的行就是观测数据中隶属度值为第k大的那个模糊集对应的行.因此，不同层次下的模糊关系矩阵为下一时刻预测提供的信息可能会在不同的行中得到体现.这点反映了在实践中不同因素对于作决策的方式和影响程度可能不一样的事实.

步骤4 综合各层次模糊关系的信息，进行预测.

在这一步中，要利用定义5中的运算把观测样本所反映的各种需要考虑的信息综合起来，为模型的预测做准备.模型预测的数学公式为

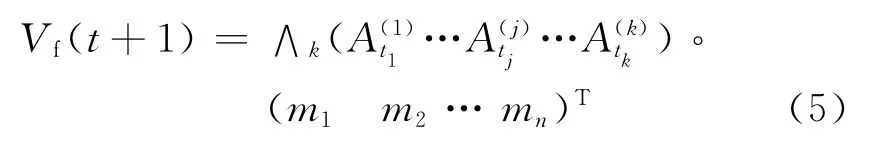
式中：Vf（t＋1）是时刻t＋1 最终的预测值；是根据观测值求得的综合信息；mi为第i个模糊区间ui的中心值（i＝1，2，…，n）.符号“。”代表着该模型对预测规则的运用方法，可以总结为如下两点：（1）如果向量全体元素都是0，则A（1）t1所对应区间的中心值作为预测值；（2）其他情况下，预测值就是模糊集对应区间中心值的加权和，权重就是归一化后得到的向量.

至此，建立了基于广义模糊逻辑的模糊时间序列模型.

2 常用的模糊区间划分方法

由于模糊区间是模糊时间序列模型建立的基石，它对于模型的计算过程和预测精度有很大影响，这方面常常是模型理论研究的第一个重点.自从Song等提出模糊时间序列模型以来，这个问题就得到了很多研究人员的重视，并在这方面有了大量的研究成果.本文将基于均匀划分、模糊C均值聚类和自动聚类等3种方法建立广义模糊时间序列模型.

2.1 均匀划分法

该方法是Song等［1－2］在1993年提出模糊时间序列模型时提出来的，它可以分成3 步：第一步，根据样本数据中的最小、最大值，分别向下、向上取整，来确定模型的论域；第二步，根据论域的大小，取一个整数作为区间的长度；最后，以该长度为基础，对论域进行均匀划分.如果论域U＝［a，b］，设l为给定的区间长度，则它的划分为ui

2.2 模糊C 均值聚类法（FCM）

这种方法的思想是根据样本数据的分布情况对区间进行划分.其中代表性的有Huarng等［8］、Yu［5］的统计法和Li等［12］提出的用优化算法寻找最优模糊子集的划分方法.本文研究的是用模糊C均值聚类划分法对样本数据进行划分，以得到的各类中心为分界点对论域进行分割.

设FCM 的目标函数如下：

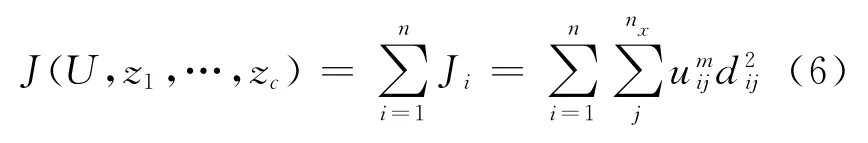
这里uij介于0到1；zi为模糊组i的聚类中心；dij＝zi－xj，为第i个聚类中心与第j个数据点间的欧几里得距离，是一个加权指数.

如果论域U＝［a，b］，设zi＜zi＋1，它的划分为

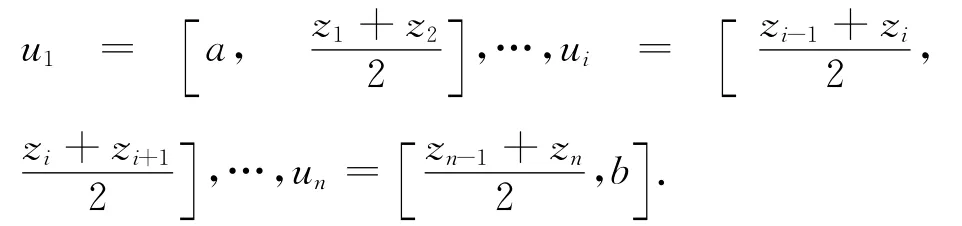
2.3 自动聚类法

这类方法的基本思路是利用适当的算法或机器学习的新方法对样本数据进行聚类分析，然后根据聚类结果确定各子区间的划分.该方法可以分为以下3步：

（1）将数据按升序排序，并去除其中的重复数据，结果形如d1，d2，d3，…，di，…，dn，并用下式计算相邻两数据差分的平均值.

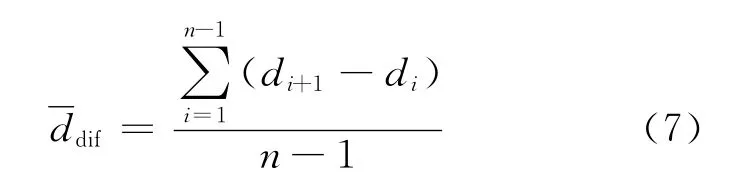
（2）将步骤（1）处理后的数据中的最小值作为当前类.根据决定下一个数据是放在当前类里，或是产生新类；

（3）根据样本数据的特征调整由步骤（2）产生的聚类.

其中第（2）步中分3种情况构建数据的类别，第（3）步中包含一些具体的操作规则，详细的算法步骤可以参见文献［6］.

总的来说，研究模糊区间分类的方法越来越多，并且新技术和方法也常被应用于这方面的研究工作中.这些方法能有效地提高模型的预测效果，特别是如果它采用了模糊聚类技术，则可以通过对聚类中心的解释来说明各个子区间所代表的实际意义.因而更符合人们的理解习惯，应用也较广，已经成为当前的研究热点.

就上述3种方法而言，基于均匀划分的方法，计算简单，应用方便.特别是在计算隶属度时，隶属函数的设置非常简单，计算比较快.该方法是模糊时间序列模型区间划分方法的“始祖”，其创新意义非常大，后来的很多模型都是以它为基础或是对它作些改进.基于FCM 的方法比第一类方法在预测精度上有很大的提高，划分后得到的区间的意义需要根据聚类结果和聚类中心进行相应的分析才能更好地理解它在模糊时间序列模型中的具体意义.然而，有些机器学习的方法对区间划分的过程是“黑箱”形式，划分的结果不容易被人们的自然语言所解释，这削弱了模糊理论在模型应用方面的优势.基于自动聚类的方法是Chen提出来的，它能根据样本数据的特征，有效地调整模糊区间的个数，提高模型的预测精度.但是它对样本数据的具体值及分布非常敏感，因而模型的稳定性不高；同时，它划分得到的区间数决定于数据本身，因而对预测结果的自然解释也不容易区分.

3 模型的应用与说明

3.1 数据说明

Alabama大学从1971 到1992年22 年间招生人数的数据是Song等提出模糊时间序列模型时用的一组数据，后来研究模糊时间序列模型的学者常将该数据作为模型的测试集.数据中最小值为13 055，最大值为19 337，常将讨论的论域定义为［13 000，20 000］.

上海股票交易综合指数是一种典型的时间序列数据，由于它数据量大，具有代表性，且股票数据也常被应用于对模型的研究，本文选择它作为第2个测试集.数据的选择范围为1997年1月1日至2006年12月31日共10年间的数据，并以每年的数据作为一个测试集，根据当年数据情况确定讨论区间的上下界，得到模型的论域，共有10组测试集.

3.2 模型说明

在建立模糊关系矩阵的过程中有3种常用的方法，为了更深入地研究广义模型的特点，下面简单介绍它们，并在后面的实验中分别讨论在这些方法下模型的预测效果.

第1种是Song等的模型［1－2］中的方法，其先定义了一个“乘”运算，将运算结果得到的矩阵表示模糊关系，然后用取最大值的方法将这些关系矩阵合成为一个模糊关系矩阵.第2 种是Chen提出的模型［3］中的方法，其建立的模糊关系矩阵R是由模糊关系是否存在而定的，即存在就定义相应位置元素为1，否则为0.这种方法计算简便，是第一种方法的改进.第3种方法中的模糊关系矩阵的元素用关系“Ai→Aj”在训练集中出现的次数取代了.

本文讨论的是在广义模糊时间序列模型的框架下，分别用均匀划分、FCM 和自动聚类3种方法对模糊区间进行划分，用Song等［1］、Chen［3］和Lee等［4］的方法建立模糊关系矩阵，然后根据对各模糊区间中心值加权的方法进行预测.实验将对模型在这3种区间划分方法和3种建立关系矩阵方法下的预测结果进行深入分析.

3.3 模型的评估标准

广义模型是一个新的模型，它同以往的模型有较大的不同，所以在对实验结果评估方面，本文采用了多种标准同时进行，它们分别是均方根误差（erms）、平均绝对误差（ema）和平均百分比误差（emap）.

4 实验结果分析

4.1 基于均匀划分的模型预测结果

表1列出了传统模型和广义模型在3种建立模糊关系矩阵方法下对入学人数预测结果的误差.3种建立模糊关系矩阵方法在表中分别记为MM1、MM2和MM3.表2中列出模型对沪市股指10年数据预测结果的平均误差.所有表的最后一行是不同建立关系矩阵方法得到结果的平均值.

从表1可以看出，广义模型采用MM1 时得到的预测误差erms分别是535.9和544.4，它们远小于原模型的932.4.即使是采用其他两种方法（MM2和MM3），也有类似的结果.这说明广义模型的预测效果要好于传统模型.从表中另外两个标准emap和ema，也能得到这样的结论.

表2也说明广义模型的预测结果要好于传统模型.此外，广义模型中参数k取2或3时，对预测结果影响不大，这是由模糊隶属度函数的定义决定的.

4.2 基于FCM 的模型预测结果

表3列出了传统模型和广义模型在3种建立模糊关系矩阵方法下对入学人数预测结果的误差.对比该表与表1和2可知，这3个评估标准所反映模型的预测效果基本相似，所以为了简便，下面只列出erms标准下模型的预测误差结果.图1描绘了基于FCM 的模型预测误差erms在股指10年数据的分布情况.

从图中可以看出，广义模型的预测结果绝大多数情况下取得更小的误差（除了广义模型（k＝3）在2004年时的情况）.但经过实验分析发现，这是由于FCM 在聚类过程中陷入局部最优时取的区间分布不合理造成的，可以通过对FCM 的改进来避免这种情况的发生.

4.3 基于自动聚类的模型预测结果

表4和5列出了传统模型和广义模型在3种建立模糊关系矩阵方法下对入学人数和股指预测结果的erms.

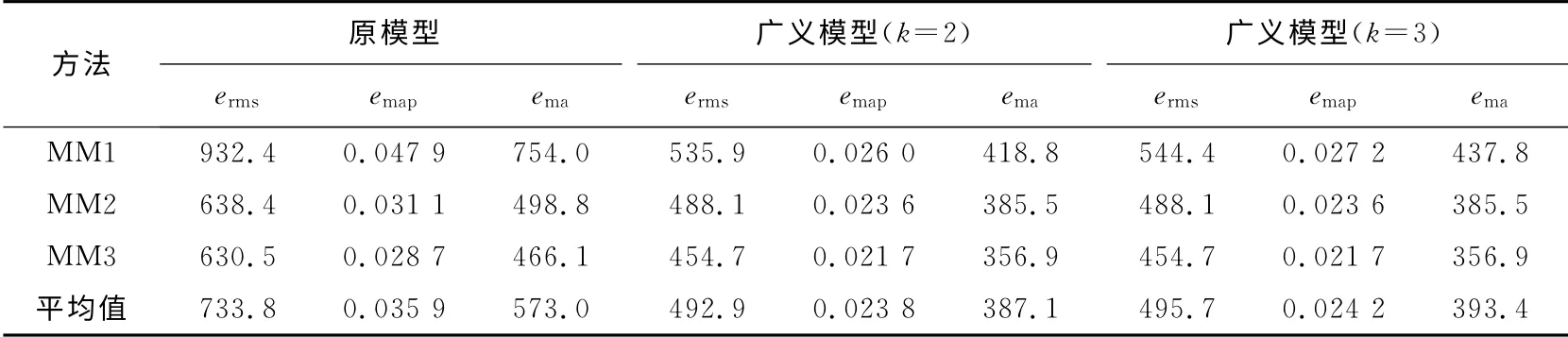
表1 均匀划分时入学人数预测误差Tab.1 Forecasting performances by using average partition on enrollment

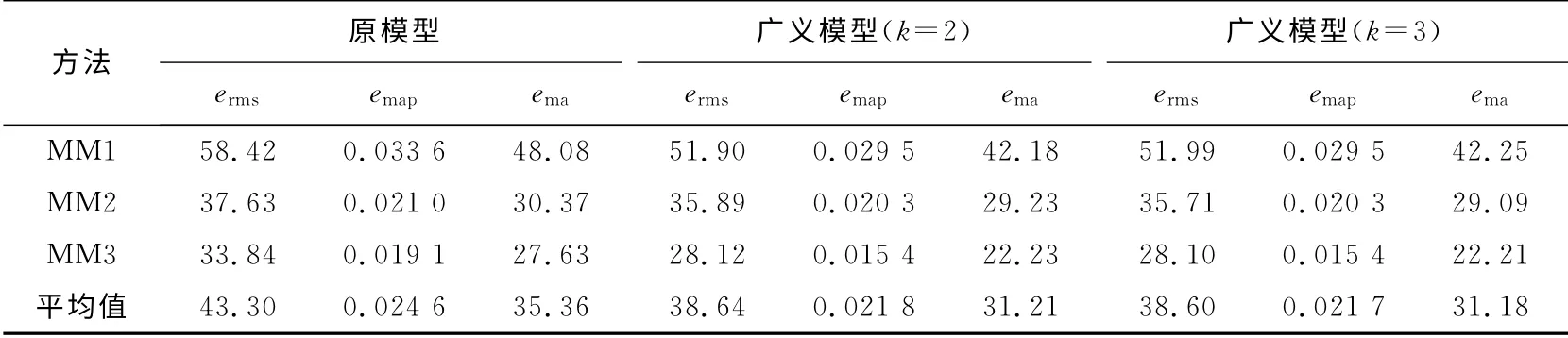
表2 均匀划分时沪市股指预测的平均误差Tab.2 Mean forecasting performances by using average partition on SSECI

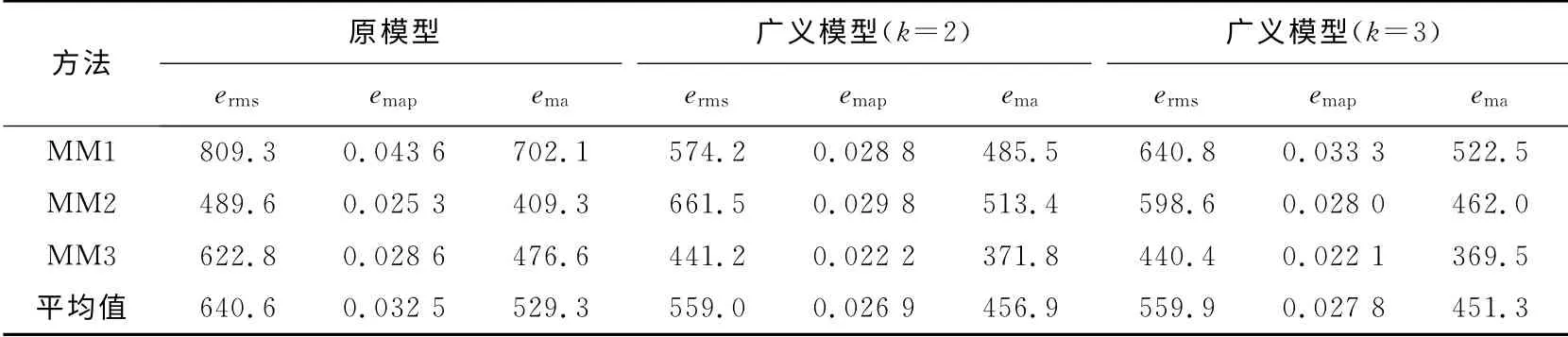
表3 FCM 划分时入学人数预测误差Tab.3 Forecasting performances by using FCM on enrollment

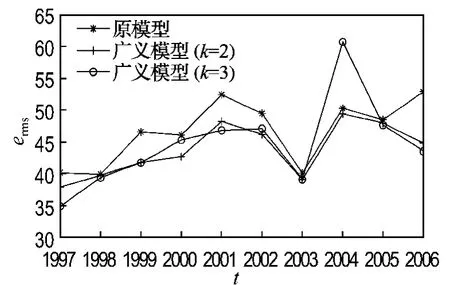
图1 FCM 划分时模型在沪市股指的预测误差ermsFig.1 erms Comparison of forecasted SSECI by using FCM

表4和5再次证明广义模型的预测效果要优于传统模型.此外，由于自动聚类方法对论域的划分较细，即模糊概念较多，这种情况下能更好地体现广义模型的优势.如表4所示，k＝3时3种关系矩阵计算方法下的误差分别是317.41、210.17、210.17，而k＝2 时 分 别 是335.69、210.17、210.17.该结果所反映的k＝3时优于k＝2时要较前面两种情况下明显.由于股指数据较丰富，表5更能明确显现广义模型在k＝3时的优势.

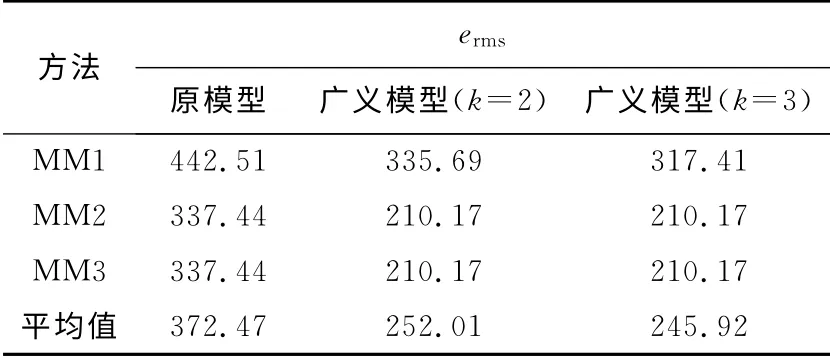
表4 自动聚类划分时入学人数预测误差ermsTab.4 ermsComparison of forecasted enrollment by using automatic clustering technique

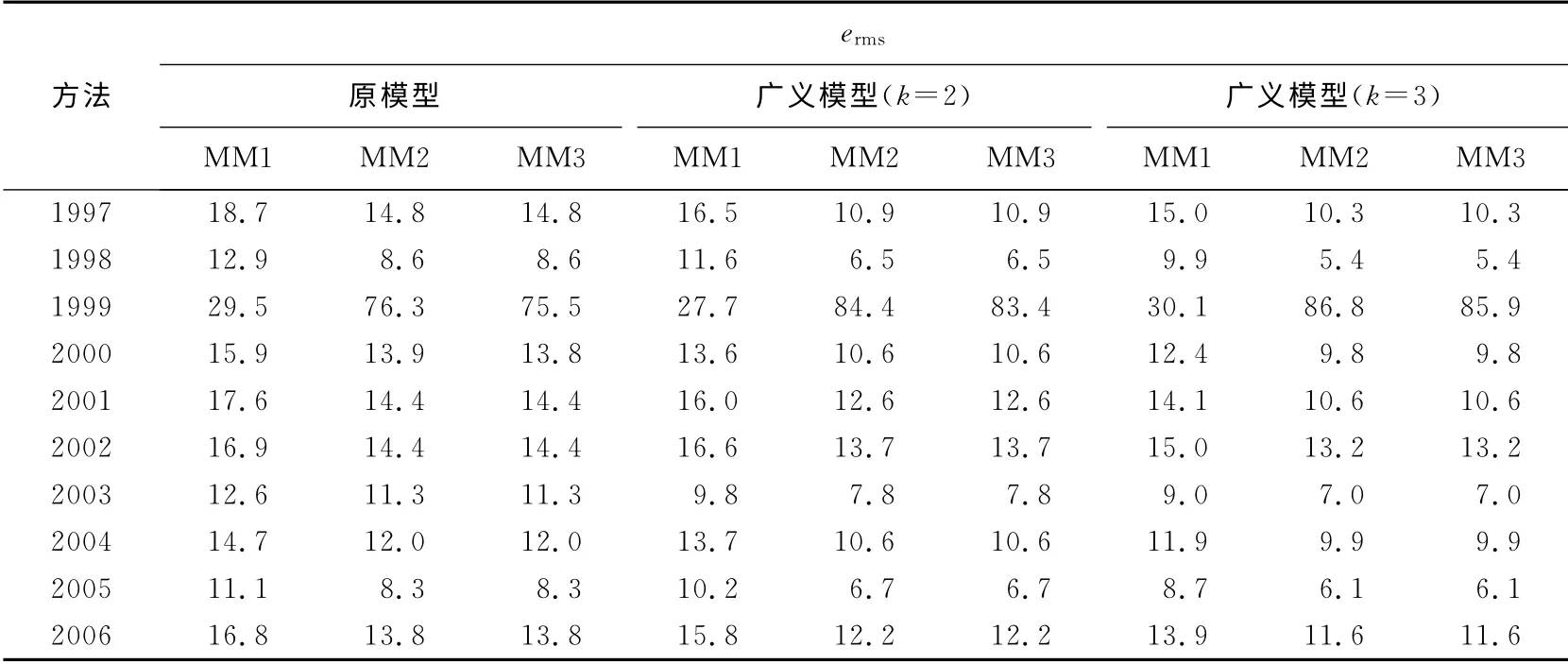
表5 自动聚类划分时沪市股指预测误差ermsTab.5 ermsComparison of forecasted SSECI by using automatic clustering technique

5 结 语

本文分别建立了模糊区间采用均匀划分、FCM 聚类和自动聚类划分时广义模糊时间序列预测模型，应用Alabama大学入学人数和沪市股指数据对广义模型与传统模型进行了深入的分析.实验结果证明广义模型能取得较传统模型更好的预测效果，而且说明模糊区间的划分对模型预测结果有较大的影响.在上述3种区间划分方法下，基于自动聚类方法的划分能得到最好的预测结果，更能体现广义模型的优势.

由于广义模糊时间序列模型的研究才刚开始，它的性质还有待于进一步研究，如模糊隶属度函数的定义对预测结果的影响，如何利用机器学习中的新算法改进广义模糊时间序列模型等.总之，对广义模糊时间序列模型的研究还有很大的空间.

［1］ SONG Qiang，Chissom B S.Forecasting enrollments with fuzzy time series.Part Ⅰ ［J］.Fuzzy Sets and Systems，1993，54（1）：1－9.

［2］ SONG Qiang，Chissom B S.Forecasting enrollments with fuzzy time series.Part Ⅱ ［J］.Fuzzy Sets and Systems，1994，62（1）：1－8.

［3］ Chen Shyi－ming.Forecasting enrollments based on fuzzy time series［J］.Fuzzy Sets and Systems，1996，81（3）：311－319.

［4］ Lee M H，Efendi R，Ismail Z.Modified weighted for enrollment forecasting based on fuzzy time series［J］.Matematika，2009，25（1）：67－78.

［5］ Yu Hui－kuang.A refined fuzzy time－series model for forecasting［J］.Physica A：Statistical Mechanics and Its Applications，2005，346（3－4）：657－681.

［6］ Chen Shyi－ming，Wang Nai－yi，Pan Jeng－shyang.Forecasting enrollments using automatic clustering techniques and fuzzy logical relationships ［J］.Expert Systems with Applications，2009，36（8）：11070－11076.

［7］ Liu Tung－kuan，Chen Yeh－peng，Chou Jyh－horng.Extracting fuzzy relations in fuzzy time series model based on approximation concepts ［J］.Expert Systems with Applications，2011，38（9）：11624－11629.

［8］ Huarng Kun－huang.Ratio－based lengths of intervals to improve fuzzy time series forecasting ［J］.IEEE Transactions on Systems，Man，and Cybernetics－Part B：Cybernetics，2006，36（2）：328－340.

［9］ QIU Wang－ren，LIU Xiao－dong，WANG Li－dong.Forecasting in time series based on generalized fuzzy logical relationship［J］.ICIC Express Letters，2010，4（5）：1431－1438.

［10］ QIU Wang－ren，LIU Xiao－dong，WANG Li－dong.Forecasting Shanghai Composite Index based on fuzzy time series and improvedC－fuzzy decision trees［J］.Expert Systems with Applications，2012，39（9）：7680－7689.

［11］ 邱望仁，刘晓东.基于证据理论的模糊时间序列模型［J］.控制与决策，2012，27（1）：99－103.QIU Wang－ren，LIU Xiao－dong.Fuzzy time series model for forecasting based on Dempster－Shafer theory［J］.Control and Decision，2012，27（1）：99－103.（in Chinese）

［12］ LI Sheng－tun，CHENG Yi－chung，LIN Su－yu.A FCM－based deterministic forecasting model for fuzzy time series［J］.Computers and Mathematics with Applications，2008，56（12）：3052－3063.

［13］ Leu Yung－ho，Lee Chien－pang，Jou Yie－zu.A distance－based fuzzy time series model for exchange rates forecasting ［J］.Expert Systems with Applications，2009，36（4）：8107－8114.

［14］ Chou Hung－lieh，Chen Jr－shian，Cheng Chinghsue，etal.Forecasting tourism demand based on improved fuzzy time series model［J］.Lecture Notes in Computer Science，2010，5990（1）：399－407.

［15］ 张 韬，冯子健，杨维中，等.模糊时间序列分析在肾综合征出血热发病率预测的应用初探［J］.中国卫生统计，2011，28（2）：146－149.ZHANG Tao，FENG Zi－jian，YANG Wei－zhong，etal.Preliminary discussion on fuzzy time series analysis for predicting the incidence rate of HFRS in China ［J］.Chinese Journal of Health Statistics，2011，28（2）：146－149.（in Chinese）