铝质亚波长圆孔阵列与牛眼结构的太赫兹波传输特性＊

陈 麟，高春梅，徐嘉明，谢 乐，朱亦鸣

（1.上海理工大学 上海市现代光学系统重点实验室，上海 200093；2.上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

近年来，太赫兹技术已越来越多地应用于通信［1］、生物化学检测［1－3］以及太赫兹成像［4－5］等，因此对太赫兹波段的窄带高性能滤波器件研究显得越来越重要。然而，就现在而言，太赫兹滤波器件的制作仍然工艺复杂、成本高，但同时，基于微结构的太赫兹器件，如双折射滤波器［6－7］却引起了科学家对电磁波超常透射现象的兴趣［8－9］。

超常光学传输现象最早于1998年，在二维（two dimensions，2D）亚波长圆孔阵列中被Ebbesen等人观测到［8］。这种超常传输能被运用在可调谐滤波器上。实验［8－10］表明，超常光学传输效应使电磁波能在原来认为是光子晶体禁带的带区中传播。进一步研究发现，超常投射的传输频率与表面等离子体激元（surface plasmon polaritons，SPPs）的共振频率相关。该结果指出，增强的投射可以归因于入射电磁波与SPPs的相互作用［11］。不久之后，Pendry等人证明了类SPPs模式的存在，同时指出，其在完美导体构成的周期性圆孔阵列上振幅与离表面距离呈指数衰减［12］。Thio等人报道了在牛眼结构上也存在类似的现象［13］，还分析了单层和双层牛眼的褶皱结构的传输过程［14］。随着厚度的减小和圆孔直径的增加，传输模式增强的现象也有报道［15］。但是，关于2D金属圆孔阵列［8－10］和牛眼结构［14］的理论和实验之间的比较却很稀缺。

1 实 验

图1 金属圆孔阵列和牛眼结构的结构示意图Fig.1 Schematic diagram of sub－wavelength hole array and bull’s eye structures

实验中使用的样品通过机械加工制作。如图1（a）所示，在0.25mm厚的纯铝质地的金属块上加工2D金属圆孔阵列。圆孔直径d为0.7mm，点阵周期s为1.13mm。图1（b）为圆孔阵列的扫描电子显微镜（scanning electron microscope，SEM）照片。如图1（c）所示在0.25mm厚的纯铝质地的金属块上加工牛眼结构。中心孔的直径g为0.3mm，周期p为0.6mm，槽的宽度l为0.3mm，槽的深度h为0.06mm。图1（d）为牛眼结构的SEM照片。

本文使用太赫兹时域光谱系统（THz time－domain spectroscopy，THz－TDS）对穿过样品的太赫兹脉冲的传输特性进行测量。为了避免水汽对太赫兹的强烈吸收，将光路的大部分放置在一个密闭的盒子中，并一直通氮气。整个实验过程中，温度和湿度一直保持在23.5～24.5℃和低于8%。

2 实验结果

图2显示了参考太赫兹脉冲（未加样品）和通过样品的太赫兹脉冲及其对应的频谱（通过傅里叶变换）。

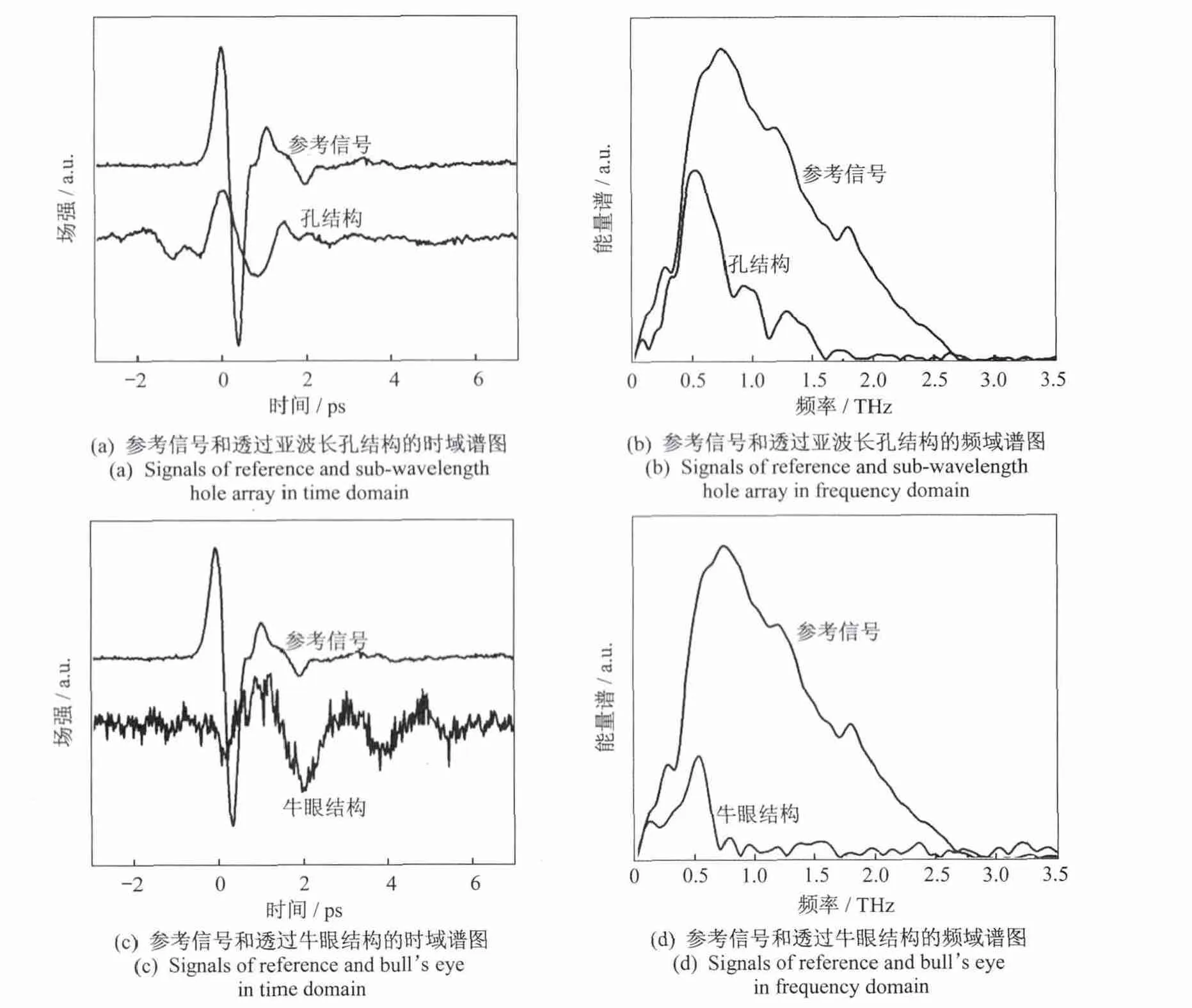
图2 圆孔阵列牛眼结构的信号谱图Fig.2 Signal spectrum of sub－wavelength hole array and bull’s eye structures

图2（a）显示了参考太赫兹脉冲以及透过样品的圆孔阵列太赫兹脉冲的时域波形。在图中，可以清楚地看到初始峰的位置精确相同，这意味着两个太赫兹脉冲波形穿透样品几乎没有延时。由于没有延时，不用考虑由于延时引起的弛豫过程，这为实现信号传输中快速响应提供了可能性。通过对两个波形首个凹陷的细致观察，可以发现样品波形相比于参考波形有轻微的下降并展宽了约0.5ps。图2（b）显示了参考太赫兹脉冲以及透过样品的圆孔阵列太赫兹脉冲的频谱，滤波效果非常明显，金属圆孔阵列的低频部分与参考信号平铺非常相近，透射峰的中心频率大约在0.53THz。太赫兹波的高频部分，尤其是高于1 THz的部分发生了急剧地衰减。通过对0.53THz参考信号和样品信号幅值的对比，发现制作的铝制圆孔阵列的投射率几乎达到了85%。

图2（c）显示了参考太赫兹脉冲以及透过样品的牛眼结构太赫兹脉冲的时域波形。在图中，可以清楚地看到，两个波形初始位置之间有约0.5ps的时间，这意味着：太赫兹信号受到了牛眼结构的阻挡。通过仔细观察，发现在初始透射峰之后存在阻尼振荡。图2（d）显示了参考信号和透过牛眼结构的样品信号通过傅里叶变换后的频谱，从图中，可以观察到明显的滤波效应。低频的牛眼结构透射信号的强度明显小于参考信号，透射峰的中心频率大约为0.53THz，而高频部分，尤其是高于0.65THz的部分被滤除。通过对0.53THz处的参考信号和样品信号幅值的进一步比较，发现牛眼结构的效率要低于圆孔阵列，只有约50%。

3 理论分析

德鲁特（Drude）模型被应用于电介质与金属表面产生的表面等离子体（surface plasmons，SPs）的理论分析中，在这个模型中，εd和εm分别代表电介质和金属的电容率，模型描绘了SPs的波矢和频率之间存在以下关系［16］：

其中，ω是电磁波的角频率，c是真空中的光速。入射电磁波能够激发界面表面自由电荷和SPs之间的耦合，但不能产生SPs。因为对于所有的SPs模式的波矢ksp都存在于光速线下的迅衰区域，无法在自由传播的光线中产生。为了使ksp下降到可以在电介质和金属表面产生SPs的非迅衰区域，需要提供一个额外的动量G［17］。

一个简单的方法是在界面上制作周期性的结构来提供所需要的动量G。对于2D的情况，动量G在x轴和y轴上正交分解成Gx和Gy两个分量，他们的振幅都为2π／a0，其中a0是制作结构的周期。对于入射角θ的入射光，可以得到［17］：

其中i、j是整数，且对于牛眼结构，i＝j。电磁场被瞬间束缚在界面上，只有表面等离激元（surface plasmon，SP）模式被保留下来并形成透射峰。

当光照射到表面上，传输过程可以分成3步：光在入射面耦合成SPs，SPs穿过圆孔到达后表面，在后边面又重新发射出电磁波。只有选择的频率能够进行上述过程。

为了对图2（b）和（d）滤波现象进行定量分析，利用有限元算法（finite element method，FEM）描述光波的传输和散射。设置入射电磁波为横磁模，空气和金属的电容率设置成：εd＝1和εm＝－5.1069×104＋i×1.2061×106，同时，在样品周围使用完美匹配层（perfect matched layers，PML）排除反射。模拟结果如图3所示，与实验结果相同。

图3（a）显示圆孔结构试验和仿真之间存在差距，实验数据显示主峰的位置在0.53THz，而模拟为0.26THz，这是由于样品周期的延展不足导致的。实验中，样品圆孔阵列中的圆孔数是有限的，从中心孔算起，最里面3圈只有6、12和16个圆孔，这导致了周期的延拓的不足，而在模拟过程中，在样品周围使用了PML边界去模拟一个无穷大的空间。

为了调查圆孔阵列中不同数量圆孔对频率漂移的影响，制作了一个相同圆孔参数且更多圆孔数的大样品。大样品包含70×70个圆孔，是小样品的100倍。图4（a）显示了大样品和小样品的频率透射率。大样品在中心频率处达到了95%的透过率，峰比小样品更窄。图4（b）显示大样品因充分的周期延拓使模拟结果更加接近于实验数据。

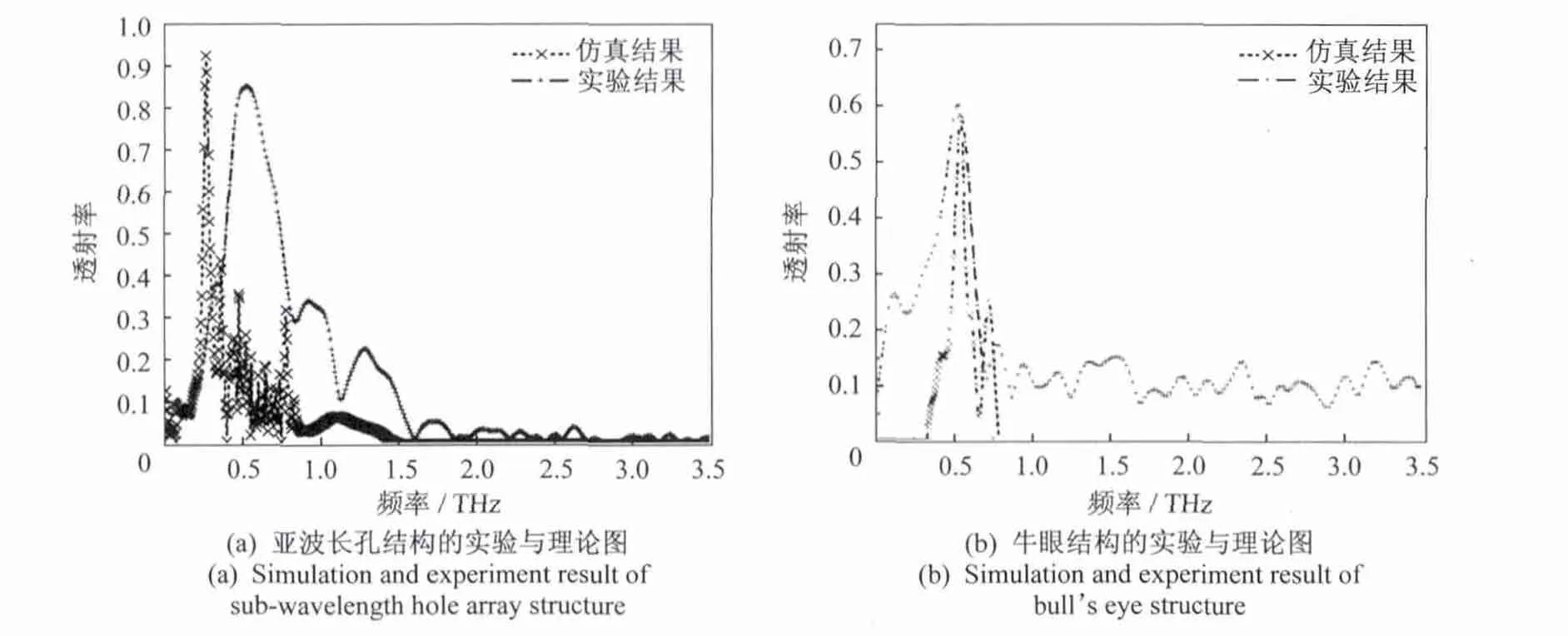
图3 实验数据和计算结果的对比Fig.3 Comparison of simulation and experiment results

图4 圆孔阵列的透射率曲线Fig.4 Transmittance of sub－wavelength hole array structure

通过实验可以得出，圆孔阵列小样品中心频率0.26THz和大样品中心频率0.53THz之间的差异主要是由周期性延拓程度决定。

对于牛眼结构来说，如图3（b）中所示，实验数据和模拟结果非常吻合，这是因为在中心孔周围已经有5圈凹槽，对于周期性延拓来说已经充分，实验和模拟的主峰中心频率都在0.53THz。在实验和模拟中都可以看到，主峰之后约0.55～0.7THz的范围内，太赫兹的信号发生剧烈地衰减，而0.75THz之上的频率被完全移除。

本文使用THZ－TDS对经过亚波长圆孔阵列和牛眼结构的太赫兹脉冲进行了实验研究。实验中，使用包含0.1～2.7THz的入射脉冲，观察到了明显的滤波效应，且滤波峰的中心频率恰好为两种结构所设计的0.53THz。太赫兹波的高频部分，尤其是高于1THz的部分发生了急剧地衰减。然而，随着大样品中圆孔数量的增加，由于更加明显的周期性，滤波峰的中心漂移到0.26THz。经使用SPPs的相关理论以及运用FEM，对超常光学透射现象和滤波效应进行分析和模拟，得到的模拟结果与实验数据非常吻合。

4 结 论

本文研究了铝制的金属圆孔阵列和牛眼结构，并用太赫兹时域光谱系统去测量太赫兹波的传输特性。实验中观测到了太赫兹波的滤波现象，入射电磁波从0.1～2.7THz，两种结构主透射峰的中心波长都为0.53THz。太赫兹波的高频部分，尤其是高于1THz的部分发生了急剧地衰减。有着更多圆孔的大样品的中心频率漂移到低频，这主要是由于周期性延拓的程度导致的。使用FEM算法进行的模拟与实验结果非常吻合。

［1］KITEAVA G K.Terahertz generation by means of optical lasers［J］.Laser Physics Letters，2008，5（8）：559－576.

［2］FEDERICI J F，SCHULKIN B，HUANG F，et al.THz imaging and sensing for security applications—explosives，weapons and drugs［J］.Semiconductor Science and Technology，2005，20（7）：S266－S280.

［3］ROGALSKI A.Infrared detectors：status and trends［J］.Progress in Quantum Electronics，2003，27（2）：59－210.

［4］肖文华，何金龙，洪 治.一种提高太赫兹波成像分辨力的方法［J］.光学仪器，2009，31（3）：35－39.

［5］王丽凤，李 璟，洪 治.连续太赫兹波成像系统检测酚醛泡沫材料中的缺陷［J］.光学仪器，2010，32（1）：13－15.

［6］WINNEWISSER C，LEWEN F，WEINZIERL J，et al.Transmission features of frequency－selective components in the far infrared determined by terahertz time－domain spectroscopy［J］.Applied Optics，1999，38（18）：3961－3967.

［7］BAUMANN F，BAILEY JR W A，NAWEED A，et al.Wet－etch optimization of free－standing terahertz frequency－selective structures［J］.Optics Letters，2003，28（11）：938－940.

［8］EBBESEN T W，LEZEC H J，GHAEMI H F，et al.Extraordinary optical transmission through sub－wavelength hole arrays［J］.Nature，1998，391（6668）：667－669.

［9］GRUPP D E，LEZEC H J，EBBESEN T W，et al.Crucial role of metal surface in enhanced transmission through subwavelength apertures［J］.Applied Physics Letters，2000，77（11）：1569－1571.

［10］BARNES W L，DEREUX A，EBBESEN T W.Surface plasmon subwavelength optics［J］.Nature，2003，424（6950）：824－830.

［11］DEGIRON A，LEZEC H J，BARNES W L，et al.Effects of hole depth on enhanced light transmission through subwavelength hole arrays［J］.Applied Physics Letters，2002，81（23）：4327－4329.

［12］PENDRY J B，MARTIN－MORENO L，GARCIA－VIDAL F J.Mimicking surface plasmons with structured surfaces［J］.Science，2004，305（5685）：847－848.

［13］THIO T，LEZEC H J，EBBESEN T W，et al.Giant optical transmission of sub－wavelength apertures：physics and applications［J］.Nanotechnology，2002，13（3）：429－432.

［14］DEGIRON A，EBBESEN T.Analysis of the transmission process through single apertures surrounded by periodic corrugations［J］.Optics Express，2004，12（16）：3694－3700.

［15］GENET C，VAN EXTER M P，WOERDMAN J P.Fano－type interpretation of red shifts and red tails in hole array transmission spectra［J］.Optics Communications，2003，225（4）：331－336.

［16］GENET C，EDDESEN T W.Light in tiny holes［J］.Nature，2007，445（7123）：39－46.

［17］RAETHER H.Surface plasmons on smooth and rough surfaces and on gratings［M］.Charlottesville：The University of Virginia，1988.