关于t－blocking集合的一个新下界＊

曹金明，沈 雁，周 瑞

（湖南大学数学与计量经济学院，湖南长沙 410082）

1 简 介

设Fq为有q个元素的有限域.PG（2，q）是Fq上的一个二维射影空间.PG（2，q）中的一个t－blocking集合定义为这样的一个点集，它与PG（2，q）中的每条直线都至少相交t个点，并且存在一条直线与之正好相交t个点.

由于t－blocking集合的多样性，不可能决定一般的t－blocking集合的精确值，所以估计t－blocking集合的元素的上下界就是自然的事情.

其中第二条的内容就是有名的Ball定理.它要求t－blocking集合不包含一条直线.在本文中，对Ball定理的条件和结论进行改进，得到了S的一个新的更大的下界，即定理1.

定理1 设S为PG（2，q）中的一个有k个元的t－blocking集合，令k＝tq＋x，则

2 主要结果

首先给出t－blocking集合中一个很重要的引理.

设K为PG（2，q）中的一个t－blocking集合.对PG（2，q）中的任意一条直线Li，我们定义ti＝K｜（1≤i≤q2＋q＋1）.并定义二元数组（P，L），其中P∈K，L为过点P的直线.

引理1 设K为PG（2，q）中的一个t－blocking集合，ti如上所示，则

证 我们通过2种不同的方法来计算所有符合条件的二元数组（P，L）的个数.

因为PG（2，q）中任意一条直线Li上有ti个点是属于K中的，即它确定了ti个不同的二元数组，而在PG（2，q）中共有q2＋q＋1条直线，所以所有符合条件的

另外也可用过点P的直线的条数来计算这些二元数组的个数.因为过点P的直线有q＋1条，即这一点确定了q＋1个二元数组，而K中点的个数总共有个，所以所有符合条件的＝（q＋1）.

下面证明定理1.

证 （ⅰ）当x≥q时，结论显然成立.

（ⅱ）当x＜q时，我们对PG（2，q）中的任意一条直线Li，定义ti＝，（1＝1，…，q2＋q＋1）.

现在来证明在PG（2，q）中每条直线上最多有S中的x个点.

利用反证法：假设PG（2，q）中存在一条直线Li0与S相交的点有x＋1个，那么Li0至少有一点Q不属于S.因为过点Q的直线有q＋1条，那么计算过点Q的q＋1条直线上S的点数.根据t－blocking集合的定义，过点Q的每条直线上至少有S上的t个点，则k≥tq＋x＋1.

这与题设k＝tq＋x矛盾.因此，每条直线上最多有S中的x个点，不属于S的点至少有q＋1－x个.显然，x≥t.

现在对PG（2，q）中所有直线上的ti求和：S，L为PG（2，q）中过点P的直线｝｜＝｜S｜（q＋1）＝k（q＋1）.

下面对PG（2，q）中所有直线上的ti－t求和：

取任意的一点N∈PG（2，q）－S，过点N的q＋1条直线分别为M1，…，Mq＋1，令mi＝，1≤i≤q＋1，得到：

因此对过点N的q＋1条直线上的mi－t求和，有：

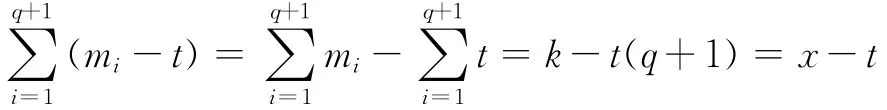
这样

现在，比较式（1）和式（2）：式（1）是对PG（2，q）中所有直线上的ti－t求和，而且PG（2，q）中的每条直线都被计算且只被计算了一次.而在式（2）中，前面已经证明了每条直线上至少有q＋1－x个点在PG（2，q）－S中，因此每条直线在式（2）中至少被重复计算了q＋1－x次.这样，就得到了关于式（1）和式（2）的不等式：

即

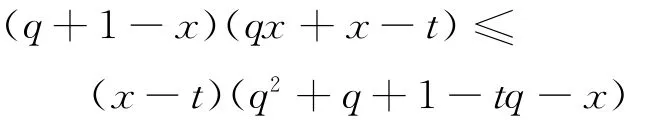
化简得：

解这个不等式：

这个结果比Ball定理要好一些，事实上，将两个结果作差，得到：

［1］ BALL S.Multiple blocking sets and arcs in finite planes［J］.J London Math Soc，1996（54）：581－593.

［2］ BLOCKHUIS A.On multiple nuclei and a conjecture of lunelli and sce［J］.Bull Belg Math Soc，1994（3）：349－353.

［3］ BRUEN A A.Polynomial multiplicities over finite fields and intersection sets［J］.J Combin Theory Ser A，1992（60）：19－33.

［4］ HILL R.Some problems concerning（k，n）－arcs in finite projective planes［J］.Rend Sem Mat Brescia，1984（7）：367－383.