钢筋混凝土构件模型的配筋率及保护层厚度研究*
黄 靓,黄梅梅,曹海信,吴志维,颜友清
(1.湖南大学土木工程学院,湖南长沙 410082; 2.北方-汉沙杨建筑工程设计有限公司,北京 100055;3.中国建筑上海设计研究院有限公司,上海 200063; 4.中天建设集团第七建设公司,广东广州 510000)
在工程实践和理论研究中,结构试验的对象大多是实际结构的模型.对于工程结构中的构件或结构的某一局部,如梁、柱、板、墙,有可能进行足尺的结构试验.但对于整体结构,除进行结构现场加载试验外,受设备能力和经济条件的限制,实验室条件下的结构试验大多为缩尺的结构模型试验.
模型是根据相似原理,用适当的比例尺和相似材料制成的与原型几何相似的试验对象,以使之在受到相似力系作用时能重演原型结构的实际工作.钢筋混凝土结构的模型试验常采用强度模型试验,强度模型研究原型结构受力全过程性能,重点是破坏形态和极限承载力,因而要求模型与原型满足强度相似条件.
在强度模型试件的设计中,材料与原型结构相同,截面几何尺寸与原型对应成比例.因而,模型的配筋面积也与原型对应成比例,即模型的配筋率与原型一致.这看似理所应当,但却未经过严格地证明.并且,模型构件的混凝土保护层厚度的取值也存在问题.当缩尺比例较大时,若将模型构件的混凝土保护层厚度按比例设计得太小,不仅难以保证施工的精度,还将影响钢筋与混凝土之间的粘结作用;若不按缩尺比例对保护层厚度进行缩小,则会影响模型与原型的相似程度.
林皋[1]等提出了结构动力模型试验与动力模型破坏试验中保持模型与原型相似的3种基本要求与处理技巧.陈星烨等[2-3]采用结构试验模型的静力和动力相似理论,提出应用方程分析与量纲矩阵分析相结合的方法,并推导了模态参数的相似比.张敏政[4]基于Bockinghamπ定理,推导了考虑建筑物活载和非结构构件质量效应的地震模拟实验的相似关系.另外,针对振动台承载能力有限等实际问题,建立了地震模拟实验的一致相似律.Timothy Hasselman[5]列举了模型的不确定性,并展示了如何通过比较分析和测试模式的一般相似结构来获得模型的不确定性.张敏政等[6]就动力相似律在小比例模型试验中的应用作了分析,探讨了结构非线弹性反应的模拟问题.Zhu等[7]对使用新型模型试验数据的结构模型分析方法进行了对比探讨.Harris[8]则系统分析了混凝土结构的动力模型.孟庆利等[9]针对钢筋混凝土小比例尺模型,提出了考虑不同材料(混凝土和配筋)间相似性协调问题的一种新型设计方法.
然而在以往的研究中,研究者多以相似原理进行动力相似的推导,虽取得了不少研究成果,但忽视了模型试验中存在的这些基本问题.在静力相似尚存在问题情况下,动力相似自然也不容易保证.因此,仍需要系统地对钢筋混凝土构件模型与原型的相似条件进行推导,研究模型参数与原型参数的关系,以确定模型试验的设计原则和模型构件配筋率及混凝土保护层厚度的取值,使模型试验能较准确地反应原型的静力学性质.下面以1,2,3,4为例推导了钢筋混凝土构件强度模型试验中的模型配筋率及保护层厚度研究.
1 钢筋混凝土柱轴心受压
轴心受压柱的受力如图1所示,承载力计算公式[10]:

式中N为轴向力设计值;φ为钢筋混凝土构件稳定系数,在矩形柱中φ与l0/b有关,l0为构件计算长度,b为矩形截面的短边尺寸.

图1 轴心受压柱的计算图形Fig.1 Calculation of axially loaded column graphic
令ρ为受压构件纵向配筋率,得到:
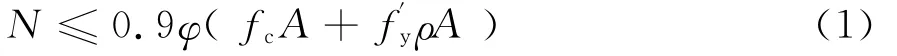
对于模型,缩尺γ倍后,模型承载力计算公式:

式中Nm为模型轴向力设计值;φm为钢筋混凝土模型稳定系数;Am为模型的截面尺寸;ρm为受压模型纵向配筋率;γ为缩尺比例.
根据量纲相似原理:Nm=N/γ2,Am=A/γ2,φ=φm(因为l0m/bm=l0/b),代入式(2)得:
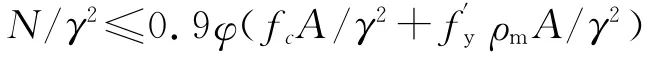
即:

对比式(1),(3)得:ρm=ρ.所以在轴心受压混凝土柱中,模型混凝土柱的纵向配筋率采取与原型柱相同的配筋率是合适的.
2 钢筋混凝土梁正截面受弯
2.1 相似性推导
梁正截面受弯如图2所示.承载力计算公式[10]:M=fcbx(h0-x/2),
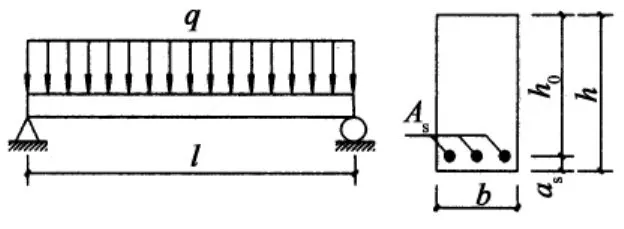
图2 梁正截面受弯的示意图Fig.2 Diagram of the beams in bending
将fcbx=fyAs=fyρA代入,得:

对于模型,缩尺γ倍后,由式(4)得模型承载力计算公式:
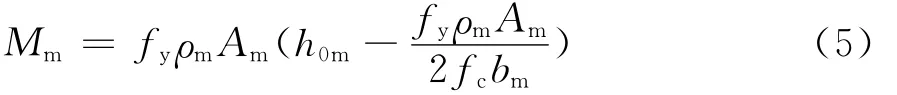
根据量纲相似原理:
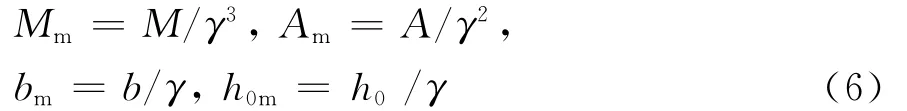
代入式(5)得:
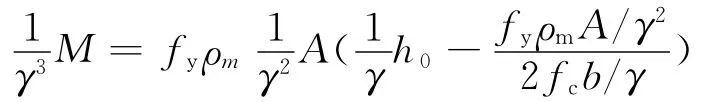
即:

对比(4),(7)得:ρm=ρ.
2.2 误差分析
事实上,2.1中的推导存在一定的问题,原因就在于式(6).该式成立的前提是模型的混凝土保护层厚度严格按缩尺比例取值,而这个条件在缩尺较大的模型试验中由于前述原因而经常不被满足.下面研究钢筋混凝土梁正截面受弯时模型构件混凝土保护层厚度的取值对极限承载力的影响.
令bm=b/γ,hm=h/γ,ρm=ρ,则Am=A/γ2,设原型与模型都只配一种直径的钢筋,且根数相同,则dm=d/γ.将h0=h-c-d/2代入式(4)得:

η反映了模型与原型的相似程度.由模型承载力值估计原型承载力值时,通常默认η=1,误差为:
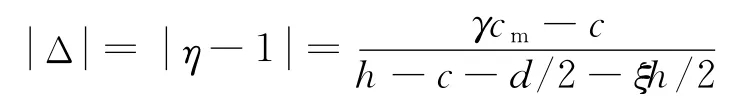
令误差小于10%,得:
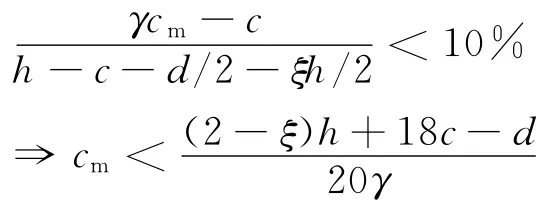
其中ξ为混凝土截面相对受压区高度,由于ξ<ξb,故上式成立的一个充分条件是:
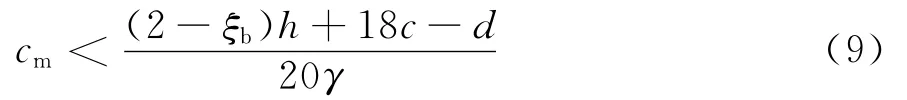
下面就梁高分别为400mm(c=30),600mm(c=40)和800mm(c=50),缩尺比例分别为2,3,4,在模型取不同保护层厚度时采用式(8)计算的η值(见表1).计算中取ξ=ξb=0.55,取钢筋直径d=20mm.
从表1中可以看到:
1)当缩尺比例γ=2时,令模型钢筋混凝土梁保护层厚度与原型梁的厚度相等,即cm=c,η基本上接近90%,基本满足误差要求;
2)当模型梁混凝土保护层厚度与原型梁的混凝土保护层厚度相同时,同样的缩尺比例,原型梁的尺寸越大,η越大,误差越小;

表1 不同参数下模型与原型承载力的相似性(用η表征)Tab.1 Similarity(expressed byη)between prototype and model with different parameters applied
3)当缩尺比例γ>2时,取cm=c,η都小于90%,γ越大,η越小,误差越大.如果模型缩尺比例γ很大,模型混凝土保护层厚度因为施工等原因不能取cm=c/γ,由表中数据知,可取cm=2c/γ,η基本上接近90%,基本满足模型试验的误差设计要求.
下面对cm的建议取值进行分析.
将ξb=0.55,d=20代入式(9)得:
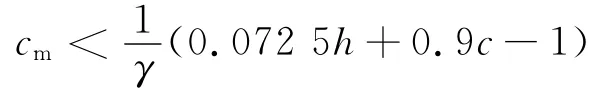
令

令h=20c-200,代入上式得:
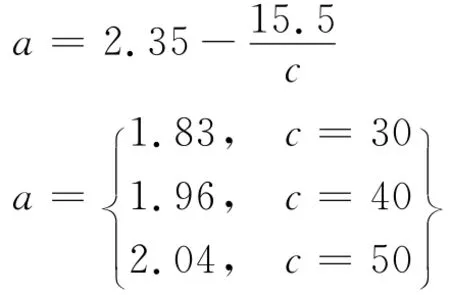
故当cm≤2 c/γ时基本满足式(9),即相似误差基本控制在10%以内.此时,取ρm=ρ是合适的.
3 钢筋混凝土梁斜截面受剪
3.1 相似性推导
不考虑弯起钢筋时的承载力计算公式[10]:

即:

对于模型,缩尺γ倍后,模型承载力计算公式:
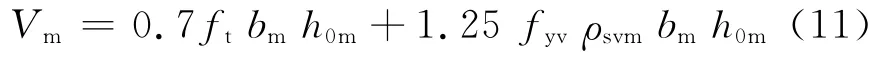
式中V,Vm分别为原型梁和模型梁的受剪承载力;h0,h0m分别为原型梁和模型梁的计算高度.
根据量纲相似原理:
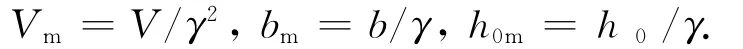
代入式(11)得:
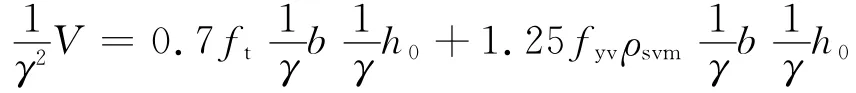
即:

对比式(10),(12)得:ρsvm=ρsv.
3.2 误差分析
将h0=h-c-d/2代入式(10),得:
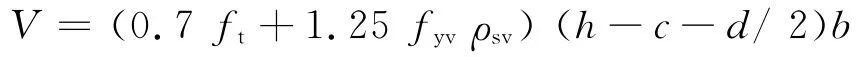
将h0m=hm-cm-dm/2代入式(11),并取ρsvm=ρsv,得:
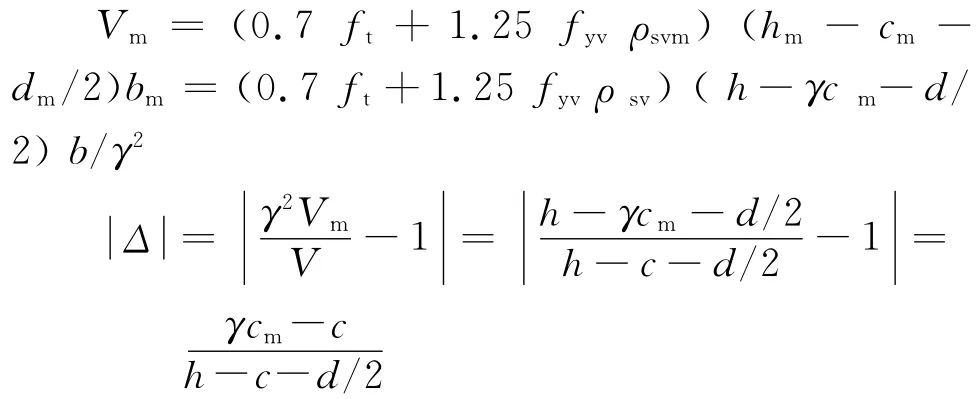
将h=20 c-200,d=20代入,并令|Δ|<10%得:

对于梁,c≥25,故a≥2.9-21/25=2.06.偏保守取a=2,即当cm≤2c/γ时由模型混凝土保护层厚度造成的相似误差小于10%.所以在钢筋混凝土梁的斜截面受剪中,在合理确定模型构件的混凝土保护层厚度的前提下,模型梁的配箍率与原型梁的配箍率相等是基本合适的.
4 钢筋混凝土柱大偏心受压
4.1 相似性推导
承载力计算公式[10]:


将式(15)代入式(14)得:
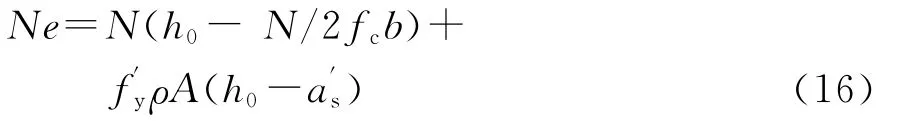
式中ρ为混凝土柱单侧配筋率,ρ=As/A=/A.
对于模型,缩尺γ倍后,模型承载力计算公式:

根据量纲相似原理:
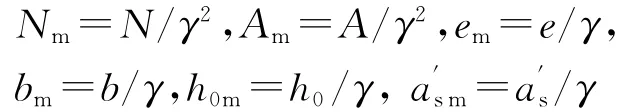
代入式(17)得:

即:

对比式(16),(18)得:ρm=ρ.
4.2 误差分析
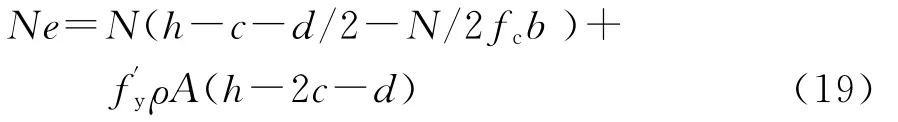
将h0=h-c-d/2,h0-a′s=h-2c-d代入式(16)得:这是关于N的二次方程,得出的表达式较复杂.为避免解方程的麻烦和便于分析误差,可以用微分来近似表示误差:dh0=-dc=c-γcm,d(h0-)=2dh0,dN=γ2Nm-N.对式(16)两边取微分,得:

式中ξh0=N/fcb.由上式可知,在模型柱配筋率与原型柱相同时,模型保护层厚度对相似误差的影响与柱的极限承载力大小有关:在偏心距足够大(式(20)分母大于0)时,随柱极限轴力的增加,式(20)的分母增大,分子减小,误差减小;在极限轴力使分母接近0时,误差将被大幅放大.而偏压构件破坏时的轴力大小与受弯状态有关,故不同的M,N组合成不同的极限状态,产生的误差不同,难以定量分析.因保护层厚度在某些情况下会对试验结果产生很大影响,故建议严格按比例设计模型,或者在设计模型时对误差进行详细分析.
5 结 论
本文针对钢筋混凝土构件模型的配筋率及保护层厚度研究,以相似理论进行推导并分析了误差,得出了如下结论:
1)在钢筋混凝土构件强度模型试验中,模型试件取与原型相同的配筋率是合适的;
2)从计算公式上看,对于钢筋混凝土轴心受压柱,模型保护层厚度不产生误差,所以可以根据方便施工或其他原则确定;
3)钢筋混凝土梁在受弯和受剪时,模型保护层厚度取原型保护层厚度除以0.5倍比例系数即cm≤2 c/γ,此时误差可以控制在10%以内;
4)钢筋混凝土柱在大偏心受压时,因保护层厚度取值而产生的误差随构件极限状态时弯矩与轴力组合的不同而不同,在轴力处于一定范围时误差将被大幅放大,建议保护层厚度严格按缩尺比例取值,否则在模型设计时应对误差进行详细分析.
[1] 林皋,朱彤,林蓓.结构动力模型试验的相似技巧[J].大连理工大学学报,2000,40(1):1-8.LIN Gao,ZHU Tong,LIN Bei.Similarity technique for dynamic structural model test[J].Journal of Dalian University of Technology,2000,40(1):1-8.(In Chinese)
[2] 陈星烨,马晓燕,宋建中.大型结构试验模型相似理论分析与推导[J].长沙交通学院学报,2004,20(1):11-14.CHEN Xing-ye,MA Xiao-yan,SONG Jian-zhong.The comparability analysis and deduction of a large structure test model[J].Journal of Changsha Communications University,2004,20(1):11-14.(In Chinese)
[3] 陈星烨,颜东煌,马晓燕.斜拉桥试验模型相似性推导与动力问题的数值分析[J].岩土力学与工程学报,2006,25(1):3206-3211.CHEN Xing-ye,YAN Dong-huang,MA Xiao-yan.Similarity deduction of test model and numerical analysis of dynamical issues for cable-stayed bridge[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(1):3206-3211.(In Chinese)
[4] 张敏政.地震模型试验中相似律应用的若干问题[J].地震工程与工程振动,1997,17(2):52-58.ZHANG Min-zheng.Study on similitude laws for shaking table tests[J].Earthquake Engineering and Engineering Vibration,1997,17(2):52-58.(In Chinese)
[5] TIMOTHY Hasselman.Quantification of uncertainty in structural dynamic models[J].Journal of Aerospace Engineering,2001,14(4):158-165.
[6] 张敏政,孟庆利,刘晓明.建筑结构的地震模拟试验研究[J].工程抗震,2003,12(4):31-35.ZHANG Min-zheng,MENG Qing-li,LIU Xiao-ming.Earthquake simulation experimental research on building structure[J].Erthquake Resistant Engineering,2003,12(4):31-35.(In Chinese)
[7] ZHU Hong-ping,HAO Xing-zhou.Comparison of analytical approaches to structural model updating using model test date[C]//Eavth &Space 2006:Engineering,Construction,and Operations in Challenging Environment.Houston:American Society of Civil Engineers,2006:1-8.
[8] HARRIS Harry G.Dynamic modeling of concrete structures[M].Detroit:American Concrete Institute,1982.
[9] 孟庆利,黄思凝,郭迅.钢筋混凝土结构小比例尺模型的相似性研究[J].世界地震工程,2008,24(4):1-6.MENG Qing-li,HUANG Si-ning,GUO Xun.Research on similarity of small scale reinforced concrete structural model[J].World Earthquake Engineering,2008,24(4):1-6.(In Chinese)
[10]GB 50010-2010 混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.GB 50010-2010 Code for design of concrete structures[S].Beijing:China Building Industry Press,2010.(In Chinese)

