高压输电导线非线性振动分析

赵桂峰，张 猛，李 杰，陈 淮

(1．郑州大学 土木工程学院，河南 郑州450001;2．同济大学 土木工程学院，上海200092)

0 引言

输电导线是电力系统中重要的载体，其安全性关系到整个电力系统的正常运行． 根据其主要力学特性，现行设计方法常采用悬索静力理论对输电线进行设计［1-4］．由于输电导线具有质量轻、阻尼小、柔度大及跨度大的特点，其风致振动明显且具有大位移小应变的几何非线性特征，尤其当输电线受到风雨激励或者强风时更易发生较强的非线性振动，严重时将会造成线路的破坏．因此，对输电导线的非线性振动进行深入研究具有重要意义． 笔者在文献［5］的基础上，基于扩展的Hamilton 原理建立了考虑初始挠度的水平悬垂输电线的三维非线性运动微分方程，按文献［2］的方法将三维问题约化为二维问题，采用Galerkin模态截断方法将连续偏微分方程离散得到相应的离散运动方程，用四阶的Runge-Kutta 方法研究了输电导线在简谐激励作用时面外振动与面内振动在主共振、超谐波共振和次谐波共振时的耦合运动特点．

1 运动方程的建立

以两端铰支在同一水平线上的弹性输电线为研究对象，将其在Oxy 平面内的初始静平衡构型S0作为参考位置，且以函数y(x)表示其在Oxy 平面的静平衡几何构型．Ec是输电线的弹性模量，Ac是其在静止状态的横截面面积，假定在振动过程中为常数;γc=mg 是单位长度输电线自重，g 是重力加速度．在外部激励F(t)作用下，输电线的三维动构型以SD表示，且外部激励在x、y、z 坐标轴的分量分别表示为F(x，t)、F(y，t)、F(z，t);u、v、w 分别为输电线沿面内纵向振动、面内横向振动和面外横向振动的位移．

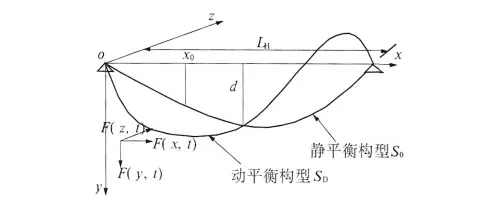
图1 输电线构型Fig．1 Configurations of conductor

采用扩展的Hamilton 原理建立输电线的三维运动方程为

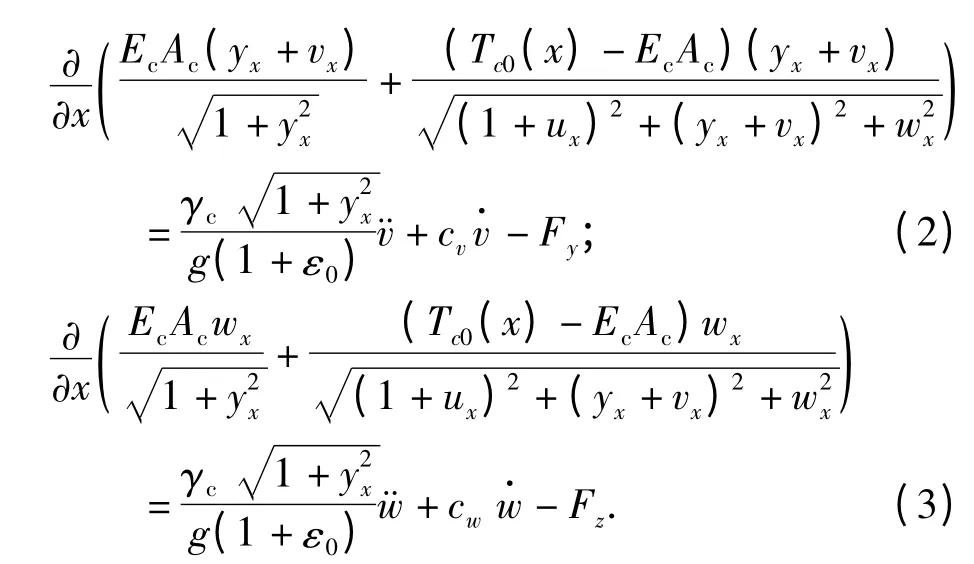
考虑实际输电线的轴向刚度EcAc较大、阻尼较小，故可其轴向惯性力和阻尼力;同时不考虑输电塔的振动对导线振动的参数激励作用． 按文献［2］的方法将上述方程约化为二维方程:

输电线属于小垂度悬索，其初始构型可用抛物线描述，取y(x)=4d(x0/LH-x20/LH)．d 为导线弧垂，LH为导线水平跨度．采用Galerkin 模态截断方法将其面内响应和面外响应表示为:

其中，各系数定义详见文献［5］．

从式(6)可见，输电线的面内和面外振动非线性耦合强烈，除线性耦合外，还包含有平方耦合和立方耦合，根据悬索线性振动理论［3］，其面外与面内振动的线性固有频率之间具有倍频关系．由非线性振动理论［2］知，输电线在一定参数条件下可发生面外与面内振动的1∶1、1∶2(或2∶1)、1∶3(或3∶1)内共振，当激励频率与系统频率满足一定关系时，输电线系统将产生主共振、1/2(1/3)次谐波共振和2 阶(3 阶)超谐波共振，同时内共振会激发非直接受激模态的振动．

2 数值分析

采用四阶的Runge-Kutta 方法，对输电线在简谐激励作用时的非线性共振以及内共振进行数值分析，以揭示其非线性振动特点．引入状态变量:

则式(6)可转化为状态方程:

由于悬索面外一阶振动的线性固有频率是其所有频率中的最小值［3］，考虑实际输电线对风荷载的敏感性可知其面外振动最易被激发，故仅研究输电线直接受面外简谐激励时非线性振动特点，即取Fy=0，Fw=Awcos(ωzt)．以下分析时均取Aw=10，初值:qv1=0，q·v1=0;qw1=1，q·w1=0．000 05．

以华东地区某高压输电线路中常见的LGJ -630/45 型号导线为例，其自重为2．06 kg/m，直径33．6 mm，截面积666．55 mm2，弹性模量63 000 MPa，拉断力141 265 N，平均运行张力35 316 N，大风(30 m/s)张力43 688 N． 最大弧垂16．6 m．水平档距480 m．可知该输电线垂跨比为1/27≪1/8，上述运动方程可用于分析其强迫振动特点．

2．1 主共振(ωz≈ωw1)和密频内共振

按悬索线性振动理论［3］，其面外振动模态取: φn(x)=sin(nπx/LH)，n=1，2，3，…相应的固有频率为

式中:H 为输电线跨中水平张力． 由上述参数可得:ωw1=0．136 4 Hz．由模态截断时的假设可知，输电线面内振动的线性固有频率ωv1与面外线性固有频率ωw1近似相等，故此条件下面外振动与面内振动存在密频内共振［4］．

为表征激励频率ωz与输电线面外固有频率ωw1的关系，引进解谐参数σ1:

ωz=kωw1+εσ1． (8)

式中:k 为非负实数;ε 为小参数．

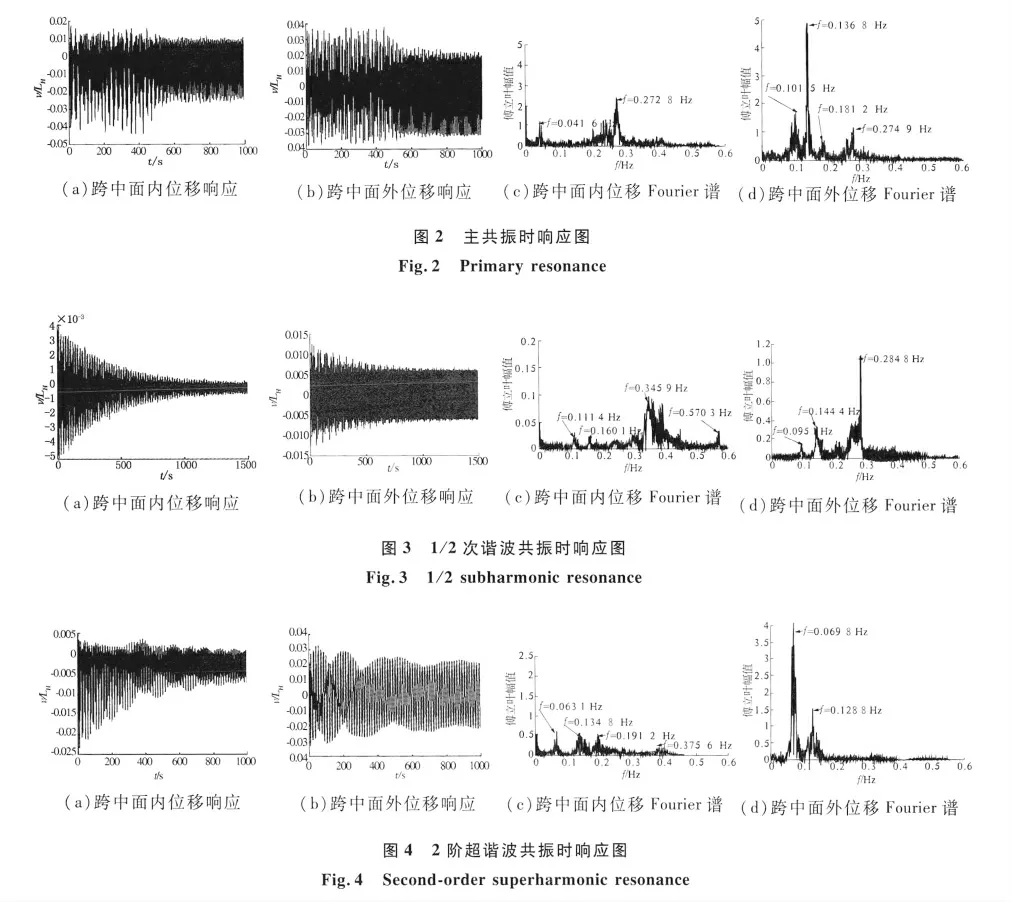
为研究系统的主共振响应，取k = 1，ε =0．001，σ1=10 并将初值条件代入状态方程(7)，计算结果见图2 所示．

由图2 可知，由于密频内共振影响，非直接受激的面内横向振动被激发，其振动具有强迫振动的特点，且稳态时其振动幅值可达到与直接受激的面外振动幅值在同一数量级． 由面外与面内振动响应时程可见，稳态时的响应具有“拍”的现象，说明面外与面内振动之间具有能量转移;虽然外激励是单频激励，且面内和面外振动取的是单模态运动，但从响应的Fourier 幅值谱可见，面外和面内振动均呈现出宽频振动特性，直接受激的面外振动以1、3 倍线性固有频率附近的宽频振动为主，而面内振动则以1/3、3 倍的线性固有频率附近的宽频振动为主，且高频振动能量不可忽视．可见密频内共振不但使面外和面内振动相互耦合，而且还对系统的振动具有调频作用．

2．2 1/2 次谐波共振(ωz≈2ωw1)和密频内共振

当激励频率ωz≈2ωw1时，系统发生1/2 次谐波共振．受激的面外振动稳态最大位移幅值是初始振幅的2．4 倍;密频内共振使得未受激的面内产生有阻尼的自由振动，但稳态时其振动并未完全衰减，而是保持有限幅值的振动;导线的振动呈现出宽频振动特性(图3(c)、(d))，面外振动以近似于1/2、1/3 和1 倍激励频率附近的模态振动为主，面内振动的能量分布在0 ～0．6 Hz 的频段内，尤其在0．3 ～0．45 Hz 频段的振动能量较大，可见密频内共振对导线的振动具有调频作用．

2．3 2 阶超谐波共振(ωz ≈1/2ωw1)和密频内共振

当激励频率ωz≈1/2ωw1时，系统发生2 阶超谐波共振．此时导线的振动具有类似于主共振时的响应特点，直接受激的面外振动产生了较大的位移，在稳态时其最大位移幅值是初始值的11倍;密频内共振使非直接受激的面内振动被激发，面外振动以近似于1、2 倍激励频率附近的振动为主(图4(d))，面内振动则以较宽频段的振动为主(图4(c))，导线的高频振动不容忽视．由此可见，密频内共振使得系统的振动特性发生了较大改变．

3 结论

采用扩展的Hamilton 原理建立水平悬垂导线的三维运动方程，并将其约化为二维振动方程，应用Galerkin 方法对其进行模态截断得到有限自由度的离散运动方程，然后使用四阶的Runge-Kutta 方法对离散方程进行数值求解，得到了导线在简谐激励作用时的面内和面外响应．研究表明:输电线结构由几何非线性可引起其面外振动模态与面内振动模态的一次方、平方与立方耦合，当面外线性固有频率与面内线性固有频率接近时，在外激励作用时导线将产生密频内共振现象，响应的能量从直接受激模态转移到非直接受激模态;几何非线性使得系统不仅有主共振发生，还将产生次谐波共振和超谐波共振，且超谐波共振时的响应远大于次谐波共振时的响应;密频内共振使得导线在主共振、次谐波共振和超谐波共振时对其振动具有明显的调频作用．

可见，由于非线性振动的调幅调频作用，使得输电线即使在外激励的幅值不大的情况下或者激励频率不等于系统固有频率时，也可因发生主共振、次谐波共振和超谐波共振而使其振幅很大．同时，在振动过程中导线面内的高频振动显著，由于面内振动(面内对称模态振动)可引起导线动张力的变化，同时导线的高频振动将使得导线与输电塔之间的耦合振动更为显著，这对于输电线路结构的安全是非常不利的．

［1］ IRVINE H M and GRIFFIN J H． On the dynamic response of a suspended cable［J］．Earthquake Engineering and Structural Dynamics，1976(4):389 -402．

［2］ NAYFEH A H，MOOK D T． Nonlinear oscillations［M］． New York:Wiley，1979．

［3］ MAX IRVINE H． Cables structures［M］．bridge:Massachusetcs The MIT Press，1981．

［4］ 白鸿柏．结构密集模态的非线性相互作用及其表现［D］． 南京:南京航空航天大学振动工程研究所，1996．

［5］ 赵桂峰．高压输电塔-线耦联体系风致非线性振动研究［D］．上海:同济大学土木工程学院，2009．