模糊层次分析法的改进及其在变压器寿命评估中的应用

杨丽徙，蔡红飞，任家印，孙 恒，郭晨光

(1．郑州大学 电气工程学院，河南 郑州450001;2．修武县电业公司，河南 修武454350)

0 引言

随着运行年限的增加以及运行工况的变化，电力变压器可能会出现各种形式的故障或故障征兆．变压器寿命评估正是从体现其运行状态的各种重要因素出发，从宏观上对变压器的运行安全状态进行整体评估［1］，进而预测变压器的剩余技术寿命，制定相应的改良措施，使设备长期处于正常安全的运行状态，延长使用年限，获得更高的经济效益．目前关于电力变压器状态评估的研究仍为热点问题［2］，也有不少基于某些技术指标对设备进行剩余寿命评估的研究成果［3］． 但是，基于变压器全寿命周期参数来构建科学合理的评估指标体系，选择合理的评估方法及指标权重，还存在许多问题需要探讨． 笔者从变压器整体健康程度入手，构建了层次型综合评估指标体系，对模糊层次分析法进行了相应改进并将其应用于变压器剩余技术寿命评估模型，降低了评估结果的主观性，提高了计算精度，实现了对电力变压器剩余技术寿命的预测．

1 改进的模糊层次分析法

1．1 模糊层次分析法的不足

在层次型的目标决策问题中经常采用模糊层次分析法［4］，该方法在处理权重问题时具有一定的优势，但同时存在着一些不足之处．

(1)采用模糊层次分析法时需利用九标度法建立互反型判断矩阵，具体标度不易准确判定，评估指标较多时，判断矩阵可能出现不满足一致性的情形［5］，必须对其进行一致性检验并加以修正，加大了判断的难度和工作量．

(2)在模糊层次分析法中常利用和行归一法求取指标权重，由于其仅考虑了判断矩阵中对应一行元素的影响，因此常不满足计算精度要求，进而不能准确地反映实际情况．

1．2 模糊层次分析法的改进

(1)设有m(m≥2)位专家，根据三标度法［6］对指标i 和指标j 进行重要程度的判定，标度准则如表1 所示．与九标度法相比较，三标度法具有简洁明了、易于判断比较的特点，有利于保证判断矩阵的一致性［7］．，该

表1 三标度法标度表Tab．1 The sheet of three-scale method

假判设定各结位果专的家数的学判期

定

望为

由此建立的优先关系矩阵F=(fij)n×n中的元素为

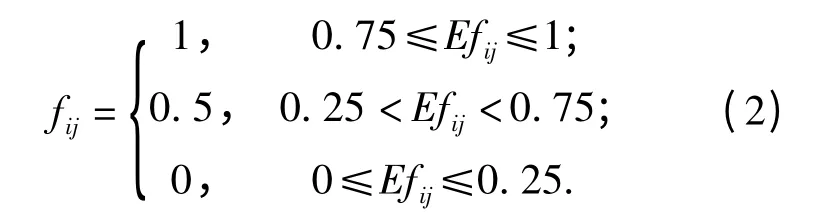
(2)将优先关系矩阵F =(fij)n×n转化为模糊一致矩阵R=(rij)n×n．先对F 进行按行求和:

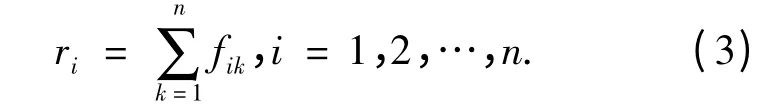
然后进行和行变换，生成元素rij:

(3)应用和行化一法求初始权重向量． 即先求取R 每行中各元素的和(不包含自身比较结果):然后求取矩阵R 中不含对角线元素的总和:则各评估指标所对应的权重值为得出指标初始权重向量为

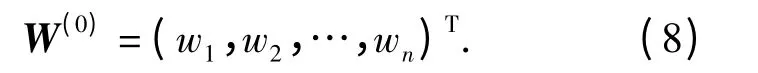
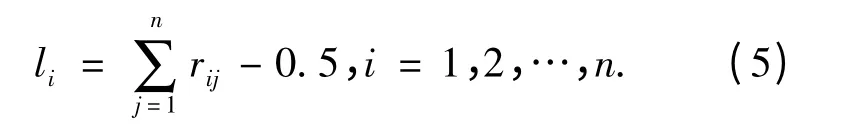
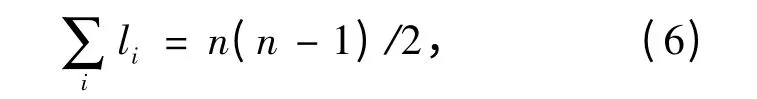
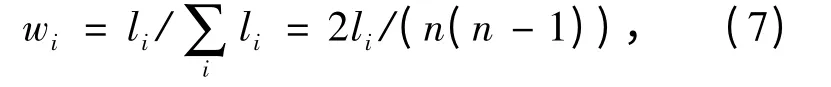
(4)利用式aij=rij/rji将R 转化为互反型矩阵A=(aij)n×n．

(5)以V0=W(0)作为特征值法的迭代初值，利用式Vk+1=A Vk求出迭代后的特征向量Vk+1，同时计算得出Vk+1的无穷范数‖Vk+1‖∞．

(6)若‖Vk+1‖∞-‖Vk‖∞＜ε(ε 为计算精度)，那么‖Vk+1‖∞就是最大特征值λmax，对Vk+1进行归一化处理后得出最终的评估指标的权重向量:

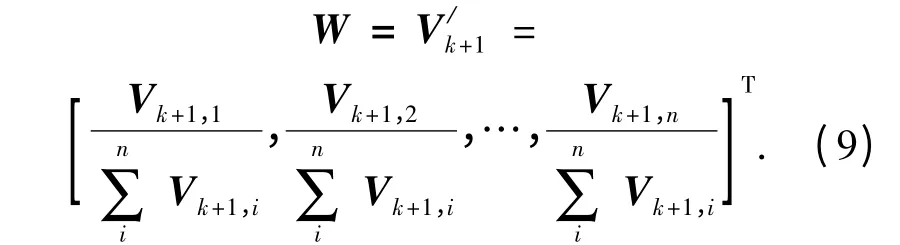
若不满足精度要求，则将

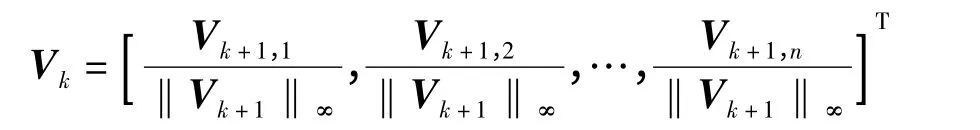
改进后的模糊层次分析法综合了多位专家的评判意见，更为合理地确定了优先关系判断矩阵，提高了判断矩阵的客观性．

2 电力变压器剩余技术寿命评估

2．1 评估指标体系的建立

依据《电力设备预防性试验规程》(DL/T 536—1996)中的规定和相关资料及文献的论述，通过对变压器产生故障原因的整理分析，按照能够影响变压器剩余技术寿命的各组成部件不同，建立了层次型综合评估指标体系如图1 所示．

图1 综合评估指标体系Fig．1 The comprehensive evaluation index system

2．2 评估指标的隶属度

如果论域U 中所包含的某个模糊子集A，对于U 中任一元素xi∈U，都指定了［0，1］闭区间中的一个数A(xi)∈［0，1］与之对应，则称A(x)为元素x 对A 的隶属函数，A(xi)越接近于1，xi从属于A 的程度越高［8］．在变压器剩余技术寿命评估过程中，需要对不同量纲、不同数量级的评估指标［9］进行隶属化处理，评估指标的隶属度越接近于1，说明指标性能越优．

对于定性指标，依据减分原则进行隶属度的求取;对于定量指标则采用常见的梯形模糊分布来求取偏小型和偏大型隶属度指标［10］．即式中:xi为第i 项指标的实测值;a 为该项指标的下限值;b 为该项指标的上限值，可以参考《电力变压器运行规程》和《电力设备预防性试验规程》确定．

2．3 欧氏贴近度和健康状态值

为了反映出被评估变压器的实际健康状态，结合评估指标权重，利用欧氏贴近度的改进公式:

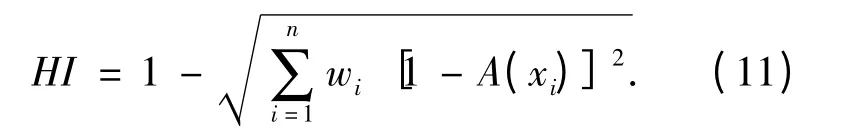
定义HI(HI∈［0，1］)为待评估对象的健康状态值．HI 值越大待评估对象的健康程度越高．

2．4 变压器剩余技术寿命的预测

电力变压器健康程度与其运行时间的关系可以表征为［11］

由于打桩机在施工过程中产生较大的噪音，如若施工地点靠近居民区则会对人们产生较大影响，通常采用消声技术进行压制砖的基础施工。这种施工方法是利用静压将桩基打入土壤中，施工质量与桩身高度、土桩长度密切相关，通常在7 m左右。在对土桩进行衔接时，可以采用锚接法、焊接法等。这种施工方法可以有效降低工程的投入成本，节约大量钢筋混凝土材料，经济实惠。

H=H0×eB×(T2-T1)． (12)

在变压器剩余技术寿命评估中，可以改进为

1 -HI=(1 -HI0)×eB×T． (13)

式中:HI0为变压器初始健康状态值;HI 为待评估时的健康状态值;B 为老化系数;T 为已运行时间．

变压器一般设计寿命为30 a，其初始健康状态值为HI0=0．95，当老化非常严重，必须退役时的健康状态值为HI退役=0．2，则老化系数为

电力变压器额定运行情况下从健康状态值HI 运行到退役健康状态值HI退役所经过的时间，即待评估变压器的固有剩余技术寿命N:

2．5 变压器剩余技术寿命的评估流程

(1)依照2．2 节中隶属度的确定方法，对各评估指标进行统一的量化处理．

(2)使用改进后的模糊层次分析法确定各层次评估指标权重．

(3)依据改进后欧氏贴近度的计算公式，利用评估指标的隶属度与其自身对应的权重值，计算出子项目层待评估变压器各部件的健康状态值HIci;以此上推，最终可得到待评估电力变压器的健康状态值HI．

(4)利用健康状态值HI，依据2．4 节中方法，计算得出待评估变压器的预期剩余技术寿命．

3 实例分析

某型号为SFPSZ1 -120000/220 的电力变压器，投入运行时间为1991 年8 月，于2004 年获取相关数据及资料，对其数据资料进行整理后，列表如表2 及表3 所示．

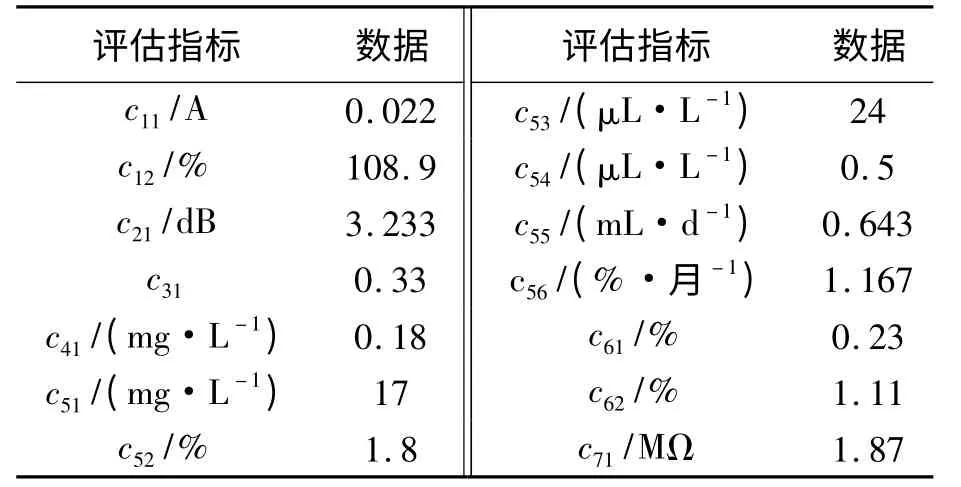
表2 定量型评估指标状态数据Tab．2 The status date of quantitative－based assessment indicators

表3 其他相关状态数据Tab．3 The other state data

(1)依据2．2 节所描述的处理方法，各待评估指标的隶属度分别如表4 所示．

(2)聘请4 位行业专家，应用三标度法对各层次评估指标进行重要程度的判定，并得到优先关系矩阵F=(fij)n×n，过程详见参考文献［12］．

(3)按照1．2 节中(2)～(6)步骤，计算得到指标层评估指标权重分别如表4 所示，子项目层权重分别为:［0．107 6，0．190 9，0．084 1，0．290 5，0．140 5，0．066 0，0．038 7，0．051 7，0．030 0］．

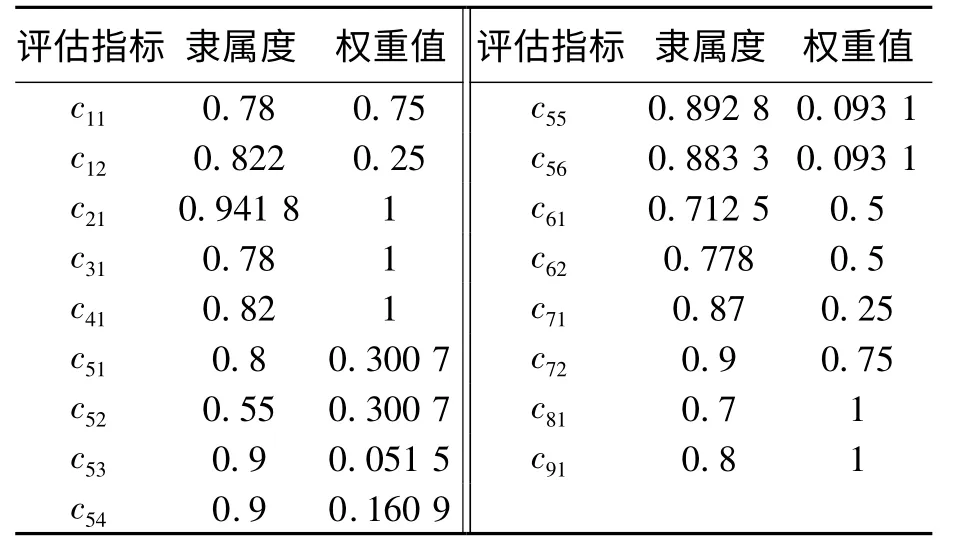
表4 评估指标隶属度及权重值Tab．4 The membership and weight values of assessment indicators

(4)将上述结果分别代入式(11)，计算可得子项目层各部件的健康状态值HIci，进而可得变压器健康状态值HI=0．800 4．

(5)依据2．4 节中计算方法，最终可得变压器预期剩余技术寿命N=15．02 年．

由评估结果可知，变压器健康状况较好，拥有较长的剩余技术寿命时间，但预计总体寿命年限略小于设计寿命．实际情况是该变压器刚进行过大修，并且曾有过负荷运行经历，与预测结果基本一致．

4 结论

(1)三标度法符合人们的思维逻辑，且形式简单，由其度量各指标之间的比较关系，减少了度量不准确的可能性，同时综合多位专家评判意见确定了优先关系判断矩阵，大大降低了判断矩阵建立的主观性;由优先判断矩阵改造而成的模糊一致性矩阵满足一致性条件，无需再进行一致性检验，减少了工作量．

(2)以和行归一法求得的目标权重向量作为特征值法的迭代初始值，进行循环迭代运算，减少了迭代次数，加快了收敛速度，提高了计算精度，使各层次评估指标的权重分配更加科学合理．

(3)将基于电力变压器各部件状态信息量的剩余技术寿命综合评估模型与模糊层次分析法结合起来，丰富了评估的依据，使评估结果更加准确并具有实际意义．

［1］ 杨丽徙，于发威，包毅．基于物元理论的变压器绝缘状态分级评估［J］． 电力自动化设备，2010，30(6):55 -58．

［2］ 王克文，蒋德珑，孙栗．电力系统状态估计算法的模糊综合评价与分析［J］． 郑州大学学报:工学版，2011，32(3):85 -89．

［3］ 李翊，肖登明，乐弘习． 糠醛含量分析与变压器剩余使用寿命的研究［J］． 华东电力，2011，39(5):0070 -0072．

［4］ 张吉军．模糊层次分析法(FAHP)［J］．模糊系统与数学，2006，14(2):80 -88．

［5］ 张俊光，程高，柯亮亮，等．基于AHP -FUZZY 算法的独塔斜拉桥安全性评价［J］．郑州大学学报:工学版，2011，32(3):85 -89．

［6］ 张琳，李长俊，苏欣，等．模糊层次分析法确定管线风险因素权重［J］．石油机械，2006，34(6):43 -45．

［7］ 李永，胡向红，乔箭．改进的模糊层次分析法［J］．西北大学学报:自然科学版，2005，35(1):11 -12．

［8］ 杨丽徙，包毅，张丹． 配电网综合评估体系的研究［J］． 郑州大学学报:工学版，2005，26(3):106-108．

［9］ 钟洪壁，高占邦，王正官，等．电力变压器检修与试验手册［M］． 北京:中国电力出版社，2000，279-284．

［10］谢季坚，刘承平．模糊数学方法及其应用［M］．2 版．武汉:华中科技大学出版社，2000:1 -20．

［11］梁博渊，刘伟，杨欣桐．变压器健康状况评估与剩余寿命预测［J］． 电网与清洁能源，2010，26(11):37-43．

［12］ 蔡红飞． 电力变压器剩余技术寿命的综合评估［D］． 郑州:郑州大学电气工程学院，2012．