大规模气泡湮灭的元胞自动机模拟

胡亚军,闫广武

(吉林大学 数学学院,长春 130012)

大规模气泡湮灭的元胞自动机模拟

胡亚军,闫广武

(吉林大学 数学学院,长春 130012)

使用元胞自动机模型,并用正六边蜂房结构代替二维均匀气泡,模拟气泡载荷超过临界载荷时大规模二维气泡湮灭过程. 结果表明,该过程存在Zipf律.

元胞自动机; 二维气泡; Zipf律

自Bak等[1-2]提出自组织临界概念以来,人们已经发现这种现象具有某种普适性,如地震、 森林火灾、 雪崩和河流的形成等都是自组织临界的[3-5]. 研究表明,对于临界的自组织系统,当能量均匀缓慢地连续加入系统中时,所引起的能量耗散是突然的、 雪崩式的； 而对于处于临界状态的系统,存在一个表示频率与尺度关系的对数直线关系,即遵从Zipf律,分形结构即为这样的系统. 自组织临界系统还有很多,如对于水的成核汽化相变,大规模气泡湮灭中可能存在自组织临界现象. 基于此,本文应用元胞自动机模型,模拟处于临界状态的气泡破裂过程. 用正六角形的蜂房结构(实际是正六角形的内切圆)代替均匀气泡. 外界能量的加入采用选定气泡的微小重量增加,研究临界重量与气泡破裂数的关系. 结果表明,该过程是自组织临界的.

1 元胞自动机模型

元胞自动机(cellular automata,又称细胞自动机,点格自动机,简称CA)是空间、 时间和状态变量完全离散的动力系统[6]. 许多相同的元胞(即点格)以均匀方式排列. 在每个格点上有一个处理器,所有处理器中都含有同样多的状态,每个元胞都处于一系列有限状态中的某种状态. 时间被离散成均匀的时刻,称为时钟. 当时钟滴答一下时,所有元胞的状态都发生改变. 元胞自动机可用于模拟许多复杂系统,特别是处于自组织临界状态的系统,例如植被的演化[7]、 生态演化[8]和交通流动[9]等.

本文考虑二维面上的一层气泡. 将气泡所在空间用正六角形蜂房结构代替,如图1所示,给出二维空间的蜂房剖分,每个正六角形的内切圆是一个气泡. 每个气泡的中心将组成与蜂房的对偶网格Di,j,每点(i,j)存在不同的水重级别,称为该点的状态值. 气泡破裂时的状态值称为临界状态值,其大于各级别的状态值. 当状态值为零时表示气泡已破裂状态. 在下一时刻,由于水重的增加使得状态值增加,超过时气泡发生破裂,并将水重均分给周围可能存在的气泡,从而构成一个多状态的元胞自动机.

图1 蜂房网格(A)和单胞及其对偶网格(B)Fig.1 Honeycomb grid (A) and unit cell and its dual grid (B)

1.1 非饱和状态 非饱和状态是指某点周围当前时刻没有破裂气泡,则此时元胞自动机的邻居数为6. 本文选择6行5列的蜂房,如图2所示. 取气泡的临界状态值为11,以3行3列位置上的气泡为起始点,当起始点的状态数增加2时,某个气泡的状态数达到11发生破裂,状态值立刻变为0. 然后将其状态值等分添加到周围,如图3所示.

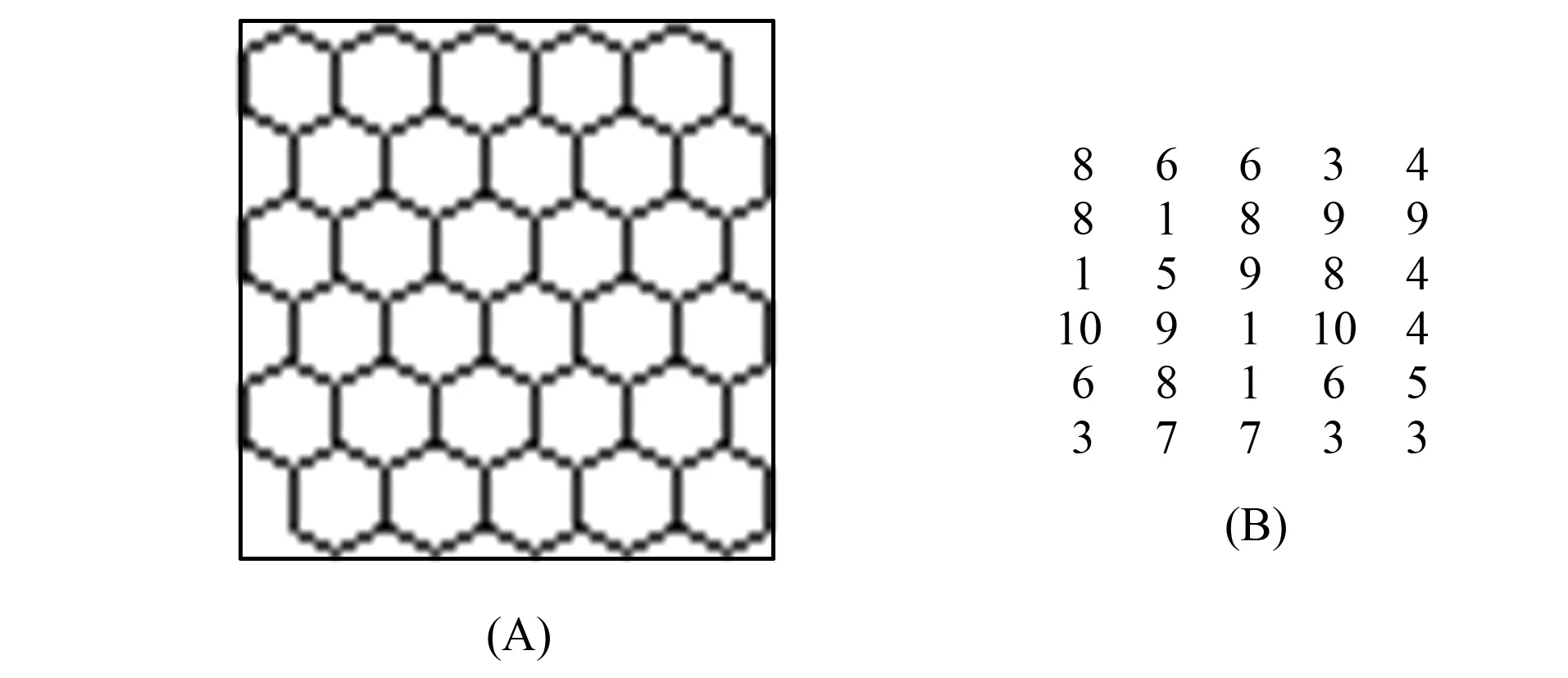
图2 6×5蜂房及级别点阵Fig.2 Honeycomb lattice 6 rows×5 columns and level

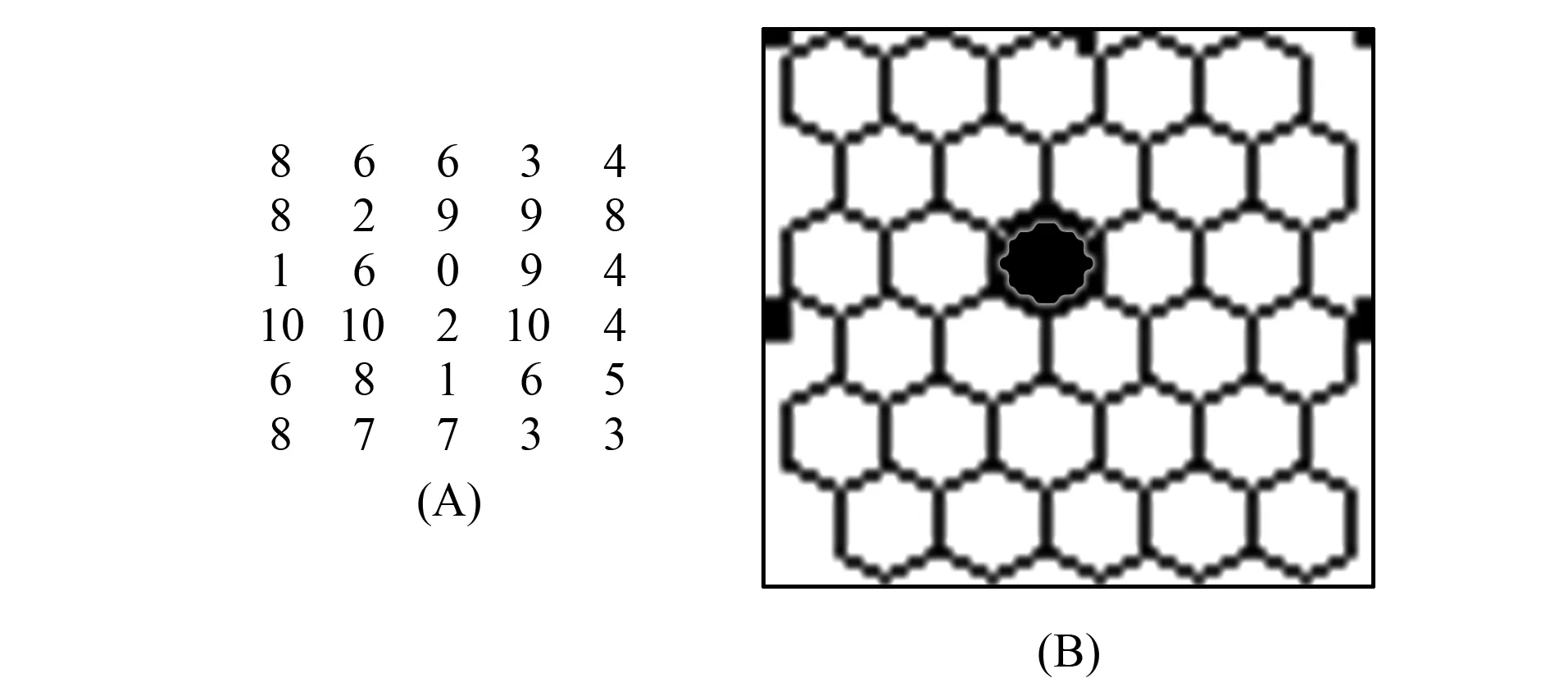
图3 下一时刻状态(A)和破裂气泡(B)(实心圆表示破裂的气泡)Fig.3 State (A) and burst bubbles (B) in the next moment (including solid circle said burst bubbles)

1.2 饱和状态 当某气泡的周围存在破裂气泡时,称该点处于饱和状态. 此时需要确定非破裂气泡数量. 例如,当周围有一个破裂气泡时,则需要将状态5均分.

1.3 气泡塌陷 气泡塌陷是指当超过临界状态时,气泡没有破裂而容易破裂,即它的临界状态值变小. 由于本文考虑的气泡是均匀且体积不变的,因此,从体积上看不出该过程,可以理解成气泡变薄,不能承受原来(上一步)时的水重,破裂状态的临界值变小. 一种极端的情况是没有塌陷过程,当前状态超过临界状态值时,气泡破裂,状态值变为零. 本文采用气泡无塌陷破裂进行模拟.

2 大规模气泡湮灭模拟

2.1 42×50气泡群 在二维平面上均匀分布42×50个气泡. 初始时刻,随机给出气泡状态. 图4为初始时刻气泡群的状态点阵,临界状态值为16.

图4 初始时刻气泡群的状态点阵Fig.4 State of bubble group in the initial moment

选择(i,j)=(20,24)为启动点,即在该点是增加水重的气泡,在模拟过程中,该点始终在增加状态值. 当该点加入的状态值为12时,有1个气泡破裂,如图5所示. 当输入状态值为56时,气泡破裂10个,如图6所示. 当输入状态值为62时,气泡破裂的图形形状有改变,但是破裂数目仍为10个,如图7所示. 继续加大输入状态值,当输入状态值增加到86时,气泡破裂17个. 破裂情况如图8所示.

图5 气泡在(i,j)=(20,24)处破裂快照Fig.5 Snapshot of the bubbles burst at location(i,j)=(20,24)

图6 输入状态值为56时气泡破裂快照Fig.6 Snapshot of bubble burst at input status value to 56

图7 输入状态值为62时气泡破裂快照Fig.7 Snapshot of bubble burst at input status value to 62

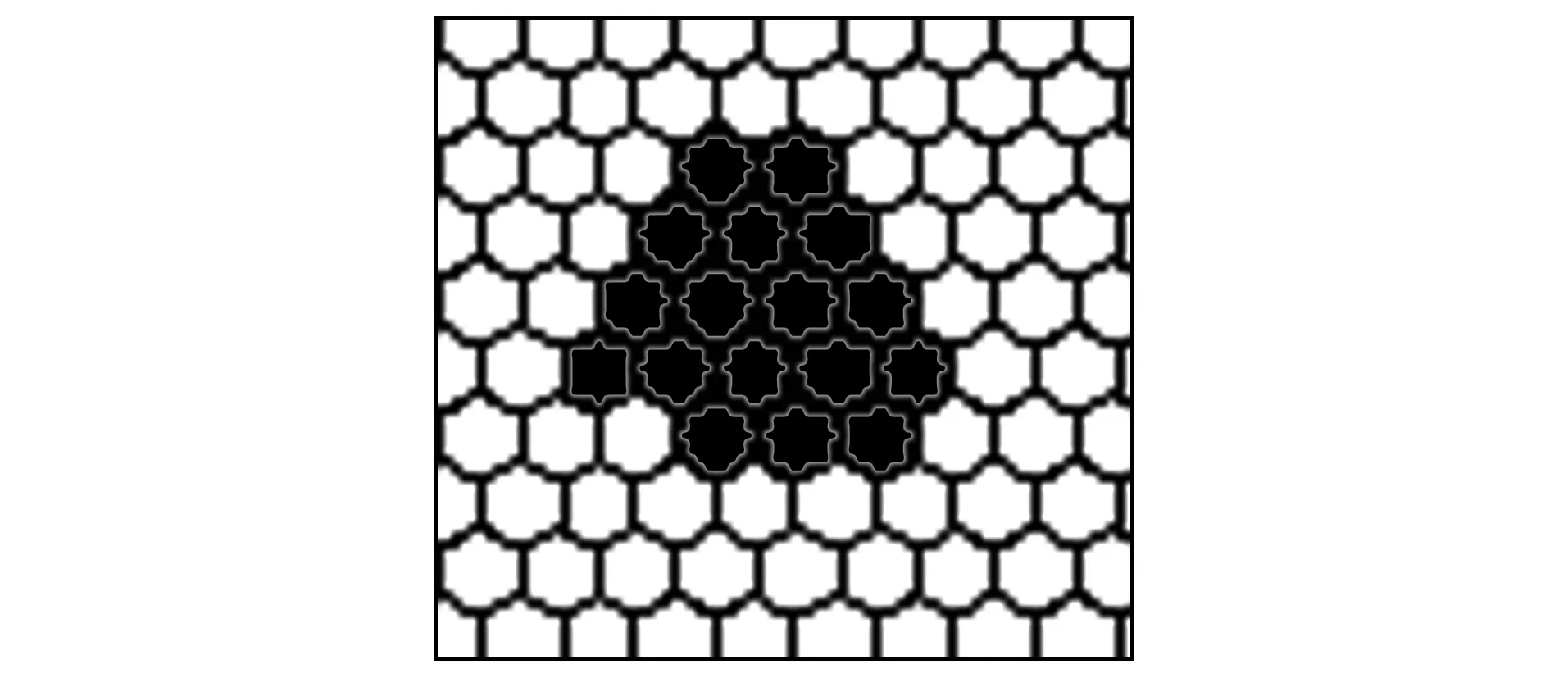
图8 输入状态值为86时气泡破裂快照Fig.8 Snapshot of bubble burst at input status value to 86

继续增加输入状态值,当输入状态值超过133时,气泡破裂的范围不再发生变化,此时整个结构已处于自组织临界状态,当输入状态值增加1时,所有气泡全部破裂,出现气泡群的湮灭现象. 图9给出了气泡破裂个数与输入状态值间的关系,由于在演化过程中,每一步增加一个状态值,因此该状态数实际上相当于时间步.

2.2 292×232气泡群 模拟292×232个气泡群的破裂情况,图10给出了气泡破裂个数与输入状态值间的关系. 模拟结果表明,该系统气泡破裂的个数只有如下6种情况: 4,5,7,19,21,83,称为系统的状态级,记K=1,2,…,6. 为了考察可能出现的Zipf定律,将上述状态级转化成Richter级:L=7-K,并给出它们之间的对数关系,如图11所示,可得一个大规模气泡湮灭的Zipf律: log(N)=Alog(L)+C,其中:A=-1.69 4;C=1.92. 结果表明,大规模气泡湮灭是自组织临界的.

图9 42×50气泡群气泡破裂个数与输入状态值间的关系Fig.9 Relationship between the 42×50 input state value and the number of bubbles burst

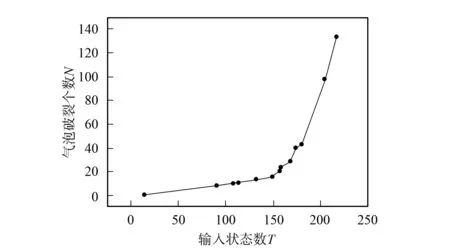
图10 292×232气泡群气泡破裂个数与输入状态值间的关系Fig.10 Relationship between the 292×232 input state value and the number of bubbles burst

图11 气泡群Richter级L与相应气泡破裂数N间的对数关系Fig.11 Corresponding logarithmic relationship between bubble burst number N and magnitude on the Richter scale L

综上可见,本文模型采用了最简单假设,仅给出了大规模气泡的湮灭现象. 真实的气泡是三维的、 大小不均匀分布的,并且具有塌陷过程. 模拟真实气泡湮灭过程需要结合实验,反复矫正模型的状态级别和临界值,同时要考虑三维非均匀分布.

[1]Bak P,TANG Chao,Wiesenfeld K,Self-organized Criticality: An Explanation of 1/fNoise [J]. Phys Rev Lett,1987,59: 381-384.

[2]Bak P,TANG Chao,Wiesenfeld K. Self-organized Criticality [J]. Phys Rev A,1988,38(3): 364-374.

[3]Bak P. How Nature Works: The Science of Self-organized Criticality [M]. New York: Springer-Verlag,1996.

[4]Seck-Tohu-Mora J C,Medina-Marino J,Martínez G J,et al. Emergence of Density Dynamics by Surface Interpolation in Elementary Cellular Automata [J]. Communications in Nonlinear Science and Numerical Simulation,2014,19(4): 941-966.

[5]Yan G W,Zhang J Y,Wang H M,et al. Simple Stochastic Lattice Gas Automaton Model for Formation of River Networks [J]. Phys Rev E,2008,78(6): 066102.

[6]闫广武. 元胞自动机与人工生命研究进展 [J]. 吉林大学学报: 理学版,2003,41(1): 40-44. (YAN Guangwu. Advances of the Studies on the Cellular Automata and Artificial Life [J]. Journal of Jilin University: Science Edition,2003,41(1): 40-44.)

[7]Ye F,Chen Q W,Li R N. Modelling the Riparian Vegetation Evolution Due to Flow Regulation of Lijiang River by Unstructured Cellular Automata [J]. Ecological Informatics,2010,5: 108-114.

[8]Ferreri L,Venturino E. Cellular Automata for Contact Ecoepidemic Processes in Predator-Prey Systems [J]. Ecological Complexity,2013,13: 8-20.

[9]XUN Jing,NING Bin,LI Keping,et al. The Impact of End-to-End Communication Delay on Railway Traffic Flow Using Cellular Automata Model [J]. Transportation Research Part C: Emerging Technologies,2013,35: 127-140.

(责任编辑： 赵立芹)

CellularAutomataSimulationforBubblesAnnihilationinaLargeNumbers

HU Yajun,YAN Guangwu
(CollegeofMathematics,JilinUniversity,Changchun130012,China)

With the help of a proposed cellular automata model for the two-dimensional bubble annihilation and a honeycomb structure instead of the two-dimensional bubbles,we simulated the process of the bubble collapse at a load beyond the critical load. This result shows the process meets Zipf’s law.

cellular automata; two-dimensional bubble; Zipf’s law

2014-02-25.

胡亚军(1990—),男,汉族,硕士研究生,从事流体力学与复杂系统的研究,E-mail： h76101@gmail.com. 通信作者: 闫广武(1964—),男,汉族,博士,教授,博士生导师,从事流体力学与复杂系统的研究,E-mail: yangw_jlu@126.com.

国家自然科学基金(批准号: 11272133).

O231.5

A

1671-5489(2014)05-0975-04