自然图像稀疏编码模型研究综述

邹柏贤，苗 军

(1．北京联合大学 应用文理学院，北京100083;2．中国科学院计算技术研究所智能信息处理重点实验室，北京100190)

0 引言

由于图像信息所占的存储空间大，对图像信息的压缩处理显得尤其重要． 如何建立新的图像分析模型，改进压缩编码算法长久以来一直是图像处理的研究热点．根据有效编码理论，人们提出自然图像的稀疏编码(Sparse Coding，SC)方法．实验证明Barlow 提出的有效编码理论的正确性，在自然刺激的条件下测试视觉神经系统响应的统计特性，发现视皮层细胞的响应满足稀疏分布［1］． 视皮层对外界刺激采用神经稀疏表示原则，可对繁杂冗余的信息进行简化和去除，由少部分神经元或基函数对图像进行的响应描述或编码表达，数据经稀疏编码后仅有少数分量同时处于明显激活状态，即呈现超高斯分布． 从数学上解释，一幅图像可以看作是一小部分基函数的线性加权组合．稀疏编码模型是模拟生物视觉系统信息加工机制的重要方法，是图像编码的有效方法．

1 稀疏编码模型研究现状

从建立SC 模型的出发点看，SC 模型可分为模拟视觉系统模型、统计分析模型两大类．模拟视觉系统模型通过仿真生物视觉感知系统，根据神经元响应的稀疏特性，对自然图像进行有效编码．从建模的方式来看，视觉模拟可分为自底向上的、自底向上与自顶向下相结合的两种建模方式． 统计模型利用传统的图像特征提取方法，建立在数字信息处理和概率统计的基础上，与人类视觉系统强大而复杂的信息处理能力相距较远．

1．1 模拟视觉系统模型

大脑视皮层感知中的一个基本问题是对于视网膜成像后的图像在视皮层中是如何进行表达．在SC 模型的矩阵形式X =AS +N 中，X 是图像灰度象素矩阵，A 是模拟初级视觉系统主视皮层V1 区感受野的特征基向量矩阵，S 是稀疏系数矢量矩阵，表示神经元对不同基图像的响应，对应主视皮层V1 区简单细胞神经元的活动状态，N 为白噪声．对自然图像进行SC 的目的是找到一个基函数表达式，使得每一个子图像块用较少的非零系数线性表示出来． 按照视觉系统模型的不同目标、特征和结构可分为6 种SC 模型．

1．1．1 最大似然概率模型

常用的自然图像SC 模型是

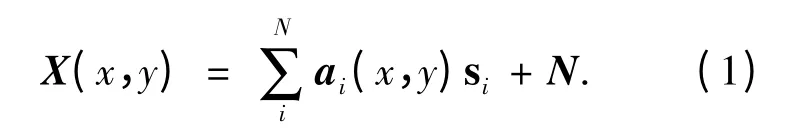
式中:X(x，y)表示图像的灰度像素值矩阵，(x，y)表示像素的空间坐标;ai表示模拟初级视觉系统主视皮层V1 区感受野的特征基向量，它是特征基矩阵A = [a1，a2，…的第i 列向量;si是稀疏系数矢量，表示主视皮层V1 区简单细胞对不同基图像的响应，系数矩阵S = [s1，s2，…T是第i 行向量． 该线性模型可使用标准梯度下降算法最大化模型(1)的似然对数实现基向量A 的学习，假定σ2是高斯噪声N 的方差，函数f(si)是指定的随机变量的分布，系数矩阵ai的梯度是:

式中:〈·〉表示随机变量的期望值;p(si)表示系数si的先验分布表示后验概率． 实际应用时，最大化模型的似然对数，取后验概率最大值作为一个样本．

1．1．2 目标函数优化模型

在学习SC 模型的参数时，把重构误差以及编码系数的稀疏性参数作为目标函数．

(1)标准稀疏编码模型．Olshausen 和Field［2］提出标准SC 模型．1996 年，Olshausen 和Field 指出自然图像经过稀疏编码后得到的基函数类似于Vl 区简单细胞感受野的反应特性，即任意给定的一幅自然图像可以用一个很大的数据集合中的少数几个非零元素来描述． 该模型中，最小化目标函数为

该模型提取的基函数模拟Vl 区简单细胞感受野的三个响应特性:空间域的局部性、时域和频域的方向性和选择性，采用随机初始化的基函数和特征系数，收敛速度慢;算法通过先验分布确定系数分量，需要根据经验选择三个函数，结果不稳定．

(2)非负稀疏编码模型． Hoyer 在标准SC 模型的基础上，提出非负SC 模型(NSC)［3］，考虑人眼以不同的通道接收非负数据，符合人眼的生理特性和主视皮层V1 区简单细胞神经元的电生理特性．把输入数据划分为对自然图像以ON、OFF通道两种方式响应的信号，系数si和特征向量ai都限定为非负值，非负的约束使得A 和S 的元素为零或者是正数，模型的最小化目标函数为:

由于模型容易受到噪声影响，尚丽等［4］考虑视觉系统对外界感知信息的自适应调整机制和视皮层之间的反馈连接，提出基于文件PCA 和V1区简单细胞感受野先验知识的反馈非负SC 模型，并且使用共轭梯度下降实现目标函数的最小化．Hoyer 给出了最小化目标函数的有效算法［5］．

(3)基于峭度稀疏性测度的稀疏编码． 尚丽［6］改进了主视皮层V1 区简单细胞感受野的SC算法．同样采用峭度的绝对值作为稀疏性度量标准，在目标函数中加入稀疏性惩罚项和图像重构误差约束，避免出现仅满足稀疏性要求而使图像重构误差变得很大． 在目标函数中加入一个固定系数的方差项，即

式中:λ1和λ2均为正常数;是预先选定的随机系数方差的尺度常数，函数第一项为图像的重构误差项，第二项为系数惩罚项，由峭度的绝对值作为稀疏性度量准则． 算法中给出基函数和系数的学习规则．

(4)任务驱动稀疏编码模型．Hoyer 等［7］在自底向上的多层感知网络结构中利用自顶向下的反馈控制建模，将线性误差最小化SC 扩展到复杂细胞输出模型，有一个权重矩阵需要学习，便于进行数据实验．简化模型底层结构的方式，使上层复杂细胞的相互作用更清晰．模型包括两个部分:复杂细胞的响应模型，另一模型把复杂细胞的输出作为输入矩阵X，用一个经典的复杂细胞能量模型，估计线性模型(1)中的稀疏向量及非负系数Si．复杂细胞对输入图像的响应是两个正交Gabor 过滤器的平方 和， C{xc，yc，θ}=

式中:G{e，xc，yc，θ)、G{o，xc，yc，θ)分别是偶、奇对称Gabor滤波器，以(xc，yc)为中心;θ 是朝向角．

Li 等［8］提出结合注意选择机制和双层反馈神经网络的编码模型，以及基于任务驱动稀疏编码模型［9］，他们认为神经细胞的响应除受稀疏编码准则的影响，保持神经细胞响应的统计独立性，还受到反馈信号的调节，使得编码能反应来自高层的知觉任务．

(5)正则图稀疏编码模型． 国内学者ZHENG Miao 等［10］提出一种正则图稀疏编码模型(Graph-SC)．假定图像矩阵X 的n 维列向量，建立一个有m 个顶点的最邻近图G，每个顶点表示一个数据向量．设W 是G 的权重矩阵，如果xi在xj的K-邻域，或xj在xi的K-邻域，则Wij= 1 ，否则，Wij= 1 ． 定义顶点xi的权重di=Wij，D =diag(d1，…，dm)．把正则图G 映射到稀疏表示系数S，最小化函数:

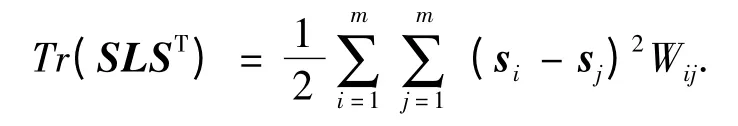
L=D -W 是拉普拉斯矩阵．那么，可以把稀疏编码模型的目标函数确定为:

参数α ≥0 ．函数中，第二项是保持正则图G到系数S 的合理性，第三项是系数S 的稀疏性，衡量非零系数(或权重较大)的数量．把优化目标函数分为两步:①固定基向量矩阵A 时学习稀疏编码S;②固定系数矩阵S 时学习基向量矩阵A．

1．1．3 Gabor 小波基函数模型

在线性SC 模型中，视网膜细胞响应是自然图像及误差的线性表示，可由Gabor 小波过滤器表示出来，称为Gabor 小波基函数稀疏编码． J．P． Jones 和L． A． Plamer 用二维Gabor 滤波器估计出最小均方误差意义下简单细胞的响应特性，证明二维Gabor 函数平移、旋转得到的小波基函数同样也具有V1 区神经元感受野的结构． 如果基函数集合是超完备的，稀疏编码效率更高． Olshausen 等人［11］提出金字塔形稀疏编码基的求解算法，假定基函数具有平移、尺度不变性，则一幅图像的全部基函数可由少量的小波滤波器和不同尺度的基函数扩展表示． L 级金字塔小波基函数模型为

利用少量的小波滤波器和不同尺度的基函数扩展得到图像的全部基函数，该算法在一定程度上提高编码效率，但是编码图像重构的精度受到影响．

1．1．4 超完备基稀疏编码模型

把自然图像X = (X1，X2，…，Xn)T表示为加上噪音的线性叠加基［12］:

X(b)= ［∑s(c)a(b，c)］+ N． (3)

其中:X(b)= {Xij}是刺激图像的向量表示;Xij是一幅图像中的像素;s(c)= {skl}是简单细胞编码的向量表示;skl是位于某个空间坐标上的编码值，简单细胞的数量是(N1× M1)，a(b，c)={aijkl}是简单细胞感受野的空间结构． Olshausen等人［13］把数学上的超完备基引入到稀疏编码．当引入超完备基的编码空间时，对输入图像的表示可能不唯一． Hubel 等人及Michison［2］的实验表明，视皮层V1 区的细胞数量远大于LGN 上的神经元数，视皮层V1 区对来自LGN 细胞刺激的响应存在超定性，可用超定基线性表示．目前常用的SC 模型都假设编码空间维数和输入空间维数相等，即都属于完备的SC 模型［14］．

1．1．5 神经网络稀疏编码模型

Cornelius Webe 等［15］建立具有适应性的SC模型，采用醒睡算法学习自下而上和自上而下双向权重，通过隐性神经元的转移函数调节稀疏性．该模型把视觉系统分为三层，即输入神经元xj、静输入神经元yi和隐性输出神经元zi，自下而上输入神经元到静输入神经元之间联结权重为Wbu，静输入神经元到隐性输出神经元之间转换函数设为z = ga，b(y)，稀疏先验指数密度函数设为函数fexp，u 为均值．由隐性输出神经元到输入神经元的自上而下重建权重是Wtd．对于静输入单元i和输入单元j，静输入神经元传递给神经元输出zi，

调节指数函数fexp使zi呈近似指数分布．这种隐性的内在稀疏表示的调节机制适用于时间尺度快速变化的情形，对于参数a 来说，可以满足变化速度在数十秒的量级，这能够解释视觉神经的倾斜后效现象．参数b 的变化范围较小，用它可以解释倾斜后效宽于指数分布的原因．Ewaldo 等［16］提出一个无监督的神经网SC 模型．

1．1．6 分层稀疏编码模型

研究者们还提出分级的SC 模型． Kai Yu［17］等提出一种两级SC 模型． 第一级对图像分块进行编码，然后被传递到第二级编码．该模型不同于传统的各分块相互独立的稀疏编码方法，各分块之间具有一定的相关性．设x1，x2，…，xn∈Rd是一幅图像的n 个分块，设X = ［x1，x2，…，xn］∈Rd×n表示这些分块的矩阵形式，A ∈Rd×p是第一级(分块级，Patch-level)的稀疏表示基向量;第二级(集合级，Set-level)基向量Φ = (φ1，φ2，…，φq)∈Rd×p，这些Φ 用来对分块x 之间统计相关性进行建模，这样可同时获得分块级和集合级的稀疏编码，最优化下述目标函数，即可得两级稀疏编码模型:

S = (s1，s2，…，sn)∈Rp×n是分块级稀疏表示系数，α ∈Rq是集合级稀疏表示系数．

该模型的特点是，考虑了不同分块之间的空间位置相关性，但是计算量大． 此外，还有DAI Dengxin 等［18］提出了三层空间稀疏编码模型(TSSC)．利用局部特征之间的相关性，用直方图交叉描述局部特征之间的相似性，建立拉普拉斯矩阵，作为稀疏编码目标函数的一部分，保持相似局部特征的稀疏表示．

1．2 统计分析模型

利用信息的低维特征建立统计分析模型，主要有独立元分析方法模型、非负矩阵分解算法模型、特定特征的稀疏编码模型等．

1．2．1 独立元分析方法

独立元分析(ICA)是典型的稀疏编码统计分析方法．在模拟视觉系统的SC 模型矩阵形式X=AS+N 中，如果不考虑高斯白噪声N，则成为独立元分析的标准数学模型X =AS．ICA 模型的条件是假定自然图像S 中的各分量独立． 大量研究表明，大多数自然图像数据服从超高斯分布，矩阵A 可以作为对自然图像稀疏表示的特征基函数的近似，ICA 算法和稀疏编码以在减少冗余的目标方面是一致的．因此，ICA 算法得到的特征基函数可作为模拟视觉系统对自然图像的稀疏编码基函数．有许多学者对独立元方法进行了改进，拓扑独立元分析方法，允许在一个小的领域内各个基向量之间有相关性，获取的自然图像的基函数的性质类似于拓扑图的形式展示出来．

1．2．2 非负矩阵分解算法

非负矩阵分解算法用于提取图像中有意义的特征．该算法是在矩阵中所有元素均为非负的条件下对其实现非负分解，由于非负性约束使得分解的基向量和组合系数中的大量元素为零或接近于零，因此这种表示方法被看作是一种稀疏编码的统计算法．

对于自然图像矩阵X，它的每一列是由一幅自然图像的象素值组成，自然图像的象素数为n，有m 个自然图像时，X ∈Rn×m．若X 是非负矩阵，那么可进行矩阵分解:X ≈WH，其中W ∈Rn×r，H ∈Rr×m，各矩阵的元素Xi，j，Wi，u，Hu，j≥0 ，0 ≤i ≤n -1 ，0 ≤j ≤m -1 ，0 ≤u ＜r -1 ，通常r ＜nm/(n + m)，根据给出的迭代关系式进行循环迭代．迭代开始前，需对X 归一化，使得所有象素值在［0，1］内，W，H 的初始值为［0，1］内的随机数．

在上述非负矩阵的分解中，W 是基矩阵，它表示图像的局部特征，H 是编码矩阵，在运用基图像和编码进行图像重构时，H 中的大多数元素为零．该计算模型的缺点在于X 的约束条件，即为非负矩阵．非负矩阵分解计算方法的收敛速度慢．国内外学多学者对此方法进行了改进，尚丽等提出具有系数度约束的局部非负矩阵分解算法LNNSC［19］，对非负矩阵分解算法做出改进．此外，国内许多学者运用非负矩阵分解算法提出了许多应用［20］．

1．2．3 特定特征模型

Huang 等人［21］从统计学角度，研究信号的稀疏统计模型，证明在一定条件下统计模型具有更好的信号重构性能．假定在线性表达式X =AS +N 中，基向量矩阵A 是固定的，在统计领域，可以用Lasso 算法对上述稀疏统计学习问题进行求解．Huang 等人发现，在具有一定特征的同组数据的S 变量往往同时为零或同时非零． Zhang 等［22］从理论上证明基于组的稀疏特性的图像标注方法可提高准确性和稳定性．

2 模型分析和比较

将各种模型的主要特点列于表1．

3 稀疏编码应用与展望

以稀疏编码为代表的生物视觉系统具有高性能的图像编码和表示能力，稀疏编码在图像、视频压缩方面具有惊人的压缩能力，可去除大量的冗余数据，广泛应用于数据降维、提取图像的关键特征和数据压缩，如何训练稀疏系数和基，使自然图像得到最短描述、降低原始数据的维数、提取关键特征，需要进一步研究解决．

首先，利用生物视点统计分析及注意选择机制建立稀疏编码模型． 研究人员对生物视点进行统计分析，在眼动及选择性注意方面取得很多研究成果，为模拟生物视觉系统的信息处理机制奠定基础．视觉系统是人类获取外部信息最重要的通道，眼动及选择性注意信息可以在细微方面反映信息提取和选择方面的过程与规律．

表1 模拟视觉系统特征模型的分类和比较Tab． 1 Classification and comparison of the simulated visual system feature model

其次，模拟生物视觉系统对各种信息的处理，提高对各类信息的识别率及处理速度．例如，提取各种不良网页信息的本质特征，对不同信息进行分类，进行快速、准确地识别和过滤．另外，随着网络和多媒体技术的发展，大量不良视频在网络上蔓延，需要客观、有效地对视频内容进行分类识别．借助人类视觉系统对视频信息关键特征的提取和处理能力，结合认知心理学、计算神经科学、统计机器学习、模式识别等方法，通过机器学习挖掘出不良视频的统计特性，提高视频分类的准确率．

第三，在视觉搜索方面上，往往采用分块编码表示图像特征，进而采用分块编码的融合，得到目标整体的稀疏编码，在独立性假设前提下利用统计推断，可应用于自动或辅助驾驶的学习和模拟．由于目前主动视觉模型的限制，对实际快速变化场景及其中的物体或目标还缺乏高效的信息抽取及编码能力，因此，稀疏编码的良好表达能力将有助于克服这些问题，使自动或辅助驾驶成为可能．

［1］ VINJE W E，GALLANT J L． Sparse coding and decorrelation in primary visual cortex during natural vision［J］． Science，2000，287(18):1273 ～1276．

［2］ OLSHAUSER B A，FIELD D J． Emergence of simplecell receptive field properties by learning a sparse code for natural images［J］． Nature，1996，381:607-609．

［3］ HOYER P O． Modeling receptive fields with non-negative sparse coding［J］． Neuroscience，2003，52 ～54(1):547 -552．

［4］ SHANG Li，CAO Feng-wen． Adaptive denoising using a modified sparse coding shrinkage method［J］． Neural Processing Letters，2006，24(2):153 -162．

［5］ HOYER P O． Non-negative sparse coding［C］∥Proceedings of the 2002 12th IEEE Workshop on Neural Networks for Signal Processing． Martigny，Switzerland，2002:557 -565．

［6］ 尚丽． 稀疏编码算法及其应用研究［D］． 北京:中科院合肥智能机械研究所，2006．

［7］ HOYER P，HYRARIEN A． A Multi-layer sparse coding network learns contour coding from natural images［J］． Vision Research，2002，42(12):1593 -1605．

［8］ LI Q Y，SHI J，SHI Z Z． A model of attention-guided visual sparse coding［C］∥Proceedings of IEEE International Conference on Cognitive Informatics，2005:120 -125．

［9］ LI Q Y，CHENG D，SHI Z Z． Task-oriented sparse coding model for pattern classification［J］． Lecture Notes in Computer Science，2005，36 (10):903-914．

［10］ZHENG Miao，BU Jia-jun，CHEN Chun，et al． Graph regularized sparse coding for image representation［J］．IEEE Transactions on Image Processing，2011，20(5):1327 -1336．

［11］ OLSHAUSEN B A，SALLEE P，LEWICKI M S．Learning sparse image codes using a wavelet pyramid architecture［J］． Advances in Neural Information Processing Systems，2001，13:887 -893．

［12］罗四维． 视觉感知系统信息处理理论［M］． 北京:电子工业出版社，2006．

［13］OLSHAUSEN B A． Principles of image representation in visual cortex［M］． The Visual Neurosciences． In:CHALUPA L M，WERNER J S． eds． Cambridge，MA:MIT Press，2002．

［14］杨谦，齐翔林，汪云九． 视皮层V1 区简单细胞的稀疏编码策略［J］． 计算物理，2001，18(2):136-143．

［15］WEBER C，TRIESCH J． A Sparse generative model of V1 simple cells with intrinsic plasticity［J］． Neural Computation，2008，20:1261 -1284．

［16］SANTANA E，PRINCEPE J C，BARROS A K，et al．Biologically inspired algorithm based on error minimization［C］// Proceedings of Brain Inspired Cognitive Systems(BICS)． Sao Luis，Brazil，2008:1 -4．

［17］YU Kai，LIN Yuan-qing，LAFFERTY J． Learning image representations from the pixel level via hierarchical sparse coding［C］∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition(CVPR)，2011:1713 -1720．

［18］DAI Deng-xin，YANG Wen，WU Tian-fu． Three-layer spatial sparse coding for image classification［C］∥Proceedings of 20th International Conference on Pattern Recognition (ICPR)，2010:613 – 616．

［19］尚丽，苏品刚，杜吉祥． 基于局部非负系数编码的掌纹识别方法［J］． 计算机应用，2011，31(6):1609 -1612．

［20］晁永国． 一种改进的非负稀疏编码图像编码方案［J］． 计算机工程与科学，2010，32(10):66 -68，69．

［21］ HUANG Jun-zhou，ZHANG Tong． The benefit of group sparsity annals of statistics［J］． Institute of Mathematical Statistics，2010，38:1978 -2004．

［22］ ZHANG Shao-ting，HUANG Jun-zhou，HUANG Yuchi，et al． Automatic image annotation using group sparsity［C］∥Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR)． San Francisco，USA:CVPR． 2010:3312 -3319．