基于小波变换的电力电缆故障测距研究

廖晓辉，梁恒娜，丁 倩

(郑州大学 电气工程学院，河南 郑州450001)

0 引言

电力电缆由于其独特的优越性在城市配电网中得到广泛应用． 但是由于在运行中受各种因素的影响，电力电缆会发生故障，因此如何快速、准确地确定故障点位置并及时处理，减少停电时间，对提高供电可靠性具有重要意义．

电力电缆故障测距法有阻抗法和行波法［1-3］．行波测距原理简单，可靠性和精度在理论上不受线路类型、故障电阻及两侧系统的影响，是目前广泛应用于电力电缆故障测距的方法． 当电力电缆发生故障时，故障点将产生向两侧母线方向运动的行波．此行波信号是一种具有突变性的、非平稳性的高频暂态信号，包含着丰富的故障信息．为了准确地提取出故障信号中的奇异点，必须对信号进行局部化分析． 传统的傅里叶分析方法是一种纯频域的全局分析方法，利用傅里叶变换分析时会把能够反映故障特征的局部信号在整个频域内平滑掉，从而丢失了用于分析故障的有用信息导致产生较大误差． 而小波分析法则是一种时频分析方法［4-7］，它能够聚焦到信号的任意细节从而实现对信号奇异性的完美描述． 笔者通过Matlab 仿真平台建立电缆故障模型，获得电缆故障仿真波形，应用小波变换进行分析，采用模极大值方法准确地从中提取有利于故障定位的行波波头的特征信息，从而提高了故障定位的准确度;同时，实测结果也表明了该方法的有效性．

1 小波变换原理

1．1 二进小波变换

小波函数的定义［3］:设函数ψ(t)∈L2(R)，L2(R)表示平方可积的实数空间，其傅里叶变换为ψ(ω)． 当ψ(ω)满足允许条件式(1)时，称ψ(t)为一个基本小波，或者称为小波母函数．

将小波母函数ψ(t)进行伸缩和平移，可以得到连续小波基函数．

式中:a ＞0，b∈R，a 为伸缩因子，b 为平移因子．

Wf(b，a)=〈f(t)，ψa，b(t)〉=

重构公式(逆变换)为

在实际应用中，尤其是通过计算机实现时，有必要对连续小波变换进行离散化，可得到二进小波变换．

如果ψj，k∈L2(R)，存在常数A 和B，且0 ＜A≤B ＜∞，使得以下稳定条件成立:

则函数序列{W2jf(k)}k∈Z称为f(t)的二进小波变换，其中，

上式相对应的逆变换为

在尺度2j下的逆变换为

Daubechies 系列小波具有正则性、正交性和紧支集，经过Daubechies 小波分解得到的高频和低频信息可以完整地反应故障信息． 随着小波变换的阶数越多，其重构信号也越接近于原始信号，但所需要的计算量也就越大． 考虑到工程应用的实际情况，笔者选择4 阶Daubechies 小波6 层分解对采集到的故障电缆行波信号进行小波分析．

1．2 信号的模极大值和奇异性检测原理

小波变换模极大值，是在尺度2j下，在t0的某一邻域，对于一切t 均有|W2jf(t)|≤|W2jf(t0)|，则称t0点为小波变换的模极大值点，W2jf(t0)称为小波变换的模极大值． 小波变换的模极大值点与信号的突变点是一一对应的．

一个突变信号在其突变点一定是奇异的． 信号的奇异性可以用Lipischitz 指数来描述．设0≤α≤1，在点t0若存在唯一常数K，对t0的邻域t 使得|f(t)-f(t0)|≤K |t-t0|α成立，则称f(t)在t0处的Lipischitz 指数是α．如果函数f(t)在t0是可微的，则α=1;如果函数在t0间断，则α=0;如果函数在t0为冲激函数，则α= -1．

信号在某一点的Lipischitz 指数非负，则在小波变换中对应的模极大值随尺度的增大而增大;在某一点的Lipischitz 指数为负，其模极大值随尺度的增大而衰减． 利用小波变换模极大值在小波分解各个尺度之间的传播特性，可以精确定位故障信号波形的突变点．

2 单端行波在线故障测距方法

电缆故障在线单端测距方法［2］是依靠故障检测时在一端记录的信号，通过波形分析找到从故障点发射来的行波波头，然后基于行波从故障点的反射时间和传播速度求取故障距离． 这种方法受到来自电缆线路对端母线行波反射波的干扰，且对采样和信号提取、衰减程度的要求高．

电缆故障可能发生在电缆的任意位置． 电缆线路MN 总长度记为L，L1为故障点距M 端的距离．如图1 所示，以线路MN 的中点O 为参考点，故障可能发生在线路前半程MO 段(如点F1处)，也可能发生在其后半程NO 段(如点F2处)．

图1 电缆故障分布图Fig．1 Distribution map of cable fault

若故障发生在线路的前半段，如图2 所示点F1处．记录下故障点的初始行波到达M 点的时间t1，反射波到达故障点后再次反射回M 点的时间t2，此时故障距离L1的计算公式如下:

图2 电缆故障在前半段时的行波分析图Fig．2 Traveling wave analysis chart of cable fault in the first half part

若故障发生在线路的后半段，如图3 所示点F2处．记录下故障点的初始行波到达M 点的时间t1，到达对端N 点后反射到M 点的时间t2，此时故障距离L1的计算公式如下:

图3 电缆故障在后半段时的行波分析图Fig．3 Traveling wave analysis chart of cable fault in the second half part

3 实例分析

3．1 仿真实例

Matlab 电力系统仿真工具箱提供了常用电力元件模型，为创建电缆故障系统模型提供了良好的平台．利用Matlab/Simulink 建立电缆故障仿真模型，如图4 所示．设电源为理想电源，用于模拟三相无穷大电源，三相变压器T1、T2 分别为Y/Δ和Y/Yg 型连接;有三条线路cb1、cb2 和cb3，其中cb2 和cb3 为正常线路，分别长20 km 和30 km，cb1 为故障相，分为两段cb1 -1 和cb1 -2，长度分别为10 km 和20 km．其中cb1 长度不变，可以改变cb1 -1 和cb1 -2 长度进行不同故障点的仿真分析，也可以改变故障模块，对同一故障点的不同故障类型进行仿真分析．

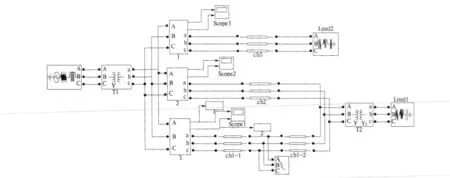
图4 电缆故障仿真模型图Fig．4 Cable fault simulation model

系统模型中的参数如下． ①系统电源:110 kV． ②变压器参数:T1，110/35 kV;T2，35/110 kV． ③电缆分布参数:正序分布参数，R1=0．079 15 Ω/km，L1=0．041 62 ×10-3H/km，C1=0．182 3 ×10-6F/km;零序分布参数，R0=0．228 1 Ω/km，L0=10 248 ×10-3H/km，C0=0．121 0 ×10-6F/km．

设置故障类型为A 相接地故障，故障时刻0．108 s，取0．107 s 到0．110 5 s 之间的采样点进行分析，采样频率为1 MHz，仿真时间0 ～0．2 s，故障波速为1．148 5 ×108m/s．

测量端显示故障电缆线路cb1 的三相电压和电流波形，图5 为A 相接地故障的电压波形．

图5 A 相接地故障电压波形Fig．5 Voltage waveform of single phase earth fault

图6 为通过db4 小波变换6 层分解后的故障相电压在各尺度下的小波系数．图中a6为小波分解得到的近似部分，d1～d6分别为高频细节系数．

采用模极大值搜索起始脉冲和反射行波的起始点之前，首先要分别确定它们的大概位置．对于脉冲变化比较平滑的信号，通常取其斜率≥±1的外测点为起始点和结束点． 通过局部模极大值搜索法得到模极大值点分别为1 088 点和1 263点．由式(9)得到故障距离为10．049 4 km ．

图6 db4 小波6 层分解的小波系数Fig．6 Wavelet coefficients of 6 layers of db4 wavelet decomposition

计算结果与实际的误差为49．4 m，相对误差0．494%． 当故障点距测量端的距离大于15 km时，采用式(10)计算故障距离．

从表1 中的电缆故障测距仿真结果可以看出，故障测距不受故障类型的影响，测量误差在1%以下，精确度提高．

3．2 实际测试

某段全长为55 m 的电缆，在其末端做开路处理，通过采样频率为100 MHz 的数据采集板采集到电缆故障行波信号，小波分析采用db1 小波2层分解，分析结果如图7 所示． 计算故障距离为54．00 m，误差较小．

表1 电缆故障测距仿真结果Tab．1 Simulation results of cable fault location

图7 实测电缆故障波形与小波分析结果图Fig．7 The measured waveform and wavelet analysis results of cable fault

4 结论

实验分析表明，采用小波分析对电缆暂态行波的采样信号处理后，利用局部模极大值法能够准确地确定行波起始脉冲和反射脉冲的时间点，从而减少外界噪声和待测线路自身因素对测距结果带来的误差;单端行波故障测距不受故障类型的影响，在不同位置的不同故障的仿真数据相对误差均小于1%，证明了该方法的可行性和精确性，从而实现故障距离的精确测量．

［1］ 徐丙垠，李胜祥，陈宗军． 电力电缆故障探测技术［M］． 北京:机械工业出版社，1999．

［2］ 刘嫣，汪梅． 一种新的电缆单端故障测距方法研究［J］．仪器仪表学报，2006，27(6):44 -45．

［3］ 何正友．小波分析在电力系统暂态信号处理中的应用［M］．西安:中国电力出版社，2011．

［4］ 王海星，许珉，谢志棠，等．基于小波变换和自相关分析的电力电缆故障测距［J］． 继电器，2005，33(12):32 -36．

［5］ 刘兵，胡勇，阮江军，等．基于小波分析频差性的电力电缆故障测距［J］． 电力自动化设备，2009，29(3):22 -26．

［6］ 马士超，刘永强． 基于小波分析的电缆故障行波测距仿真研究［J］．现代电力，2010，27(6):16 -20．

［7］ 于泽，费明． 基于小波变换和行波法的电缆故障测距方法研究［J］． 科学技术与工程，2011，11(34):344 -347．