大吨位液压裂管器液压系统可靠性研究

吕刚，原思聪，欧阳恒

(1.西安建筑科技大学机电工程学院，陕西西安710055;2.中国兵器工业第203 研究所，陕西西安710065)

大吨位液压裂管器是一种用于地下管线非开挖置换的技术装备。非开挖技术是指利用岩土导向技术和定向钻进技术，在地表不开挖和地层结构破坏极小的情况下对各种地下管线进行铺设、修复或更换的一种新技术。该技术具有不影响交通、不破坏环境、施工周期短、综合成本低、施工安全性好等优点，特别适合于一些无法进行开挖作业的区域，如穿越闹市区、文物保护区、公路、铁路、建筑物、河流等。

目前，随着环保要求的提高和城镇化的发展，液压裂管器的使用率也逐步提高。因此研究液压裂管器液压系统的可靠性，对于提高其使用效率、降低维护成本、延长经济寿命，都具有重大意义。

1 液压裂管器液压系统介绍

液压裂管器液压系统原理图如图1所示，分为5个独立的子系统:主伸缩子系统、前夹紧子系统、后夹紧子系统、拧卸子系统和动力头旋转子系统。

液压系统工作时，每一个工作过程都包括两种典型工况——装杆和卸杆。下面分别就这两种典型工况的动作顺序加以说明。

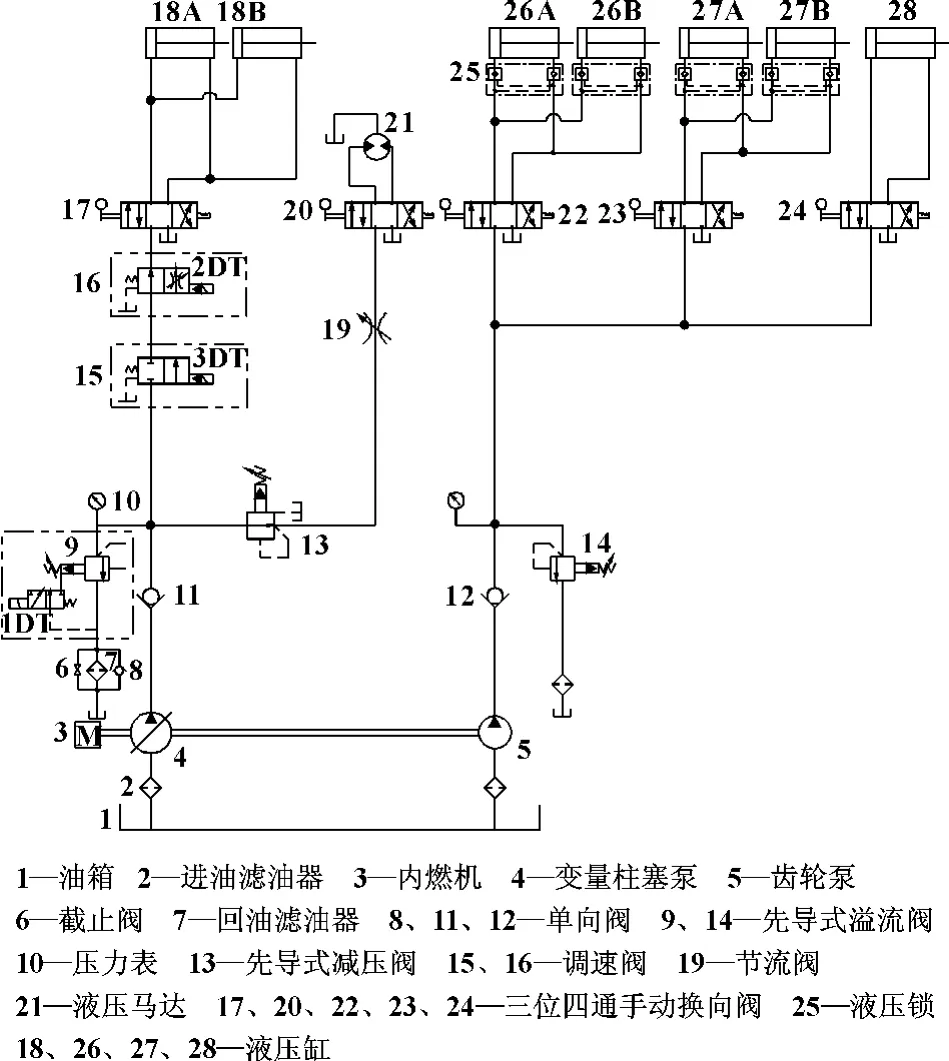
图1 液压裂管器液压系统原理图

1.1 装杆工况

操作工将第一根拉杆放入后夹紧装置中，后夹紧缸27 将拉杆一端的阳螺纹头夹住，动力头马达21 正转，动力头上所带阳螺纹与拉杆另一端所带阴螺纹咬合上紧，动力头旋转子系统压力上升，溢流阀9 溢流，马达21 停止转动。然后后夹紧油缸27 松开，液压缸18 前行至最大行程处停止。前夹紧缸26 夹紧拉杆的阴螺纹头处，动力头马达21 反转，动力头上所带阳螺纹与拉杆阴螺纹脱离。动力头马达21 停止转动，液压缸18 退后至初始位置。

操作工将第二根拉杆放入后夹紧装置中，并用手使第二根拉杆的阳螺纹与第一根拉杆的阴螺纹旋合上，动力头马达21 正转，待螺纹上紧后，动力头马达21 停转，前夹紧缸26 松开，液压缸18 前行至最大行程处停止，前夹紧缸26 夹紧拉杆的阴螺纹头处，动力头马达21 反转，螺纹脱开。液压缸18 退后至初始位置。操作工放入第三根拉杆，重复上述动作。

1.2 卸杆工况

当第一根拉杆拉出后，前后夹紧缸分别夹紧相临两根拉杆的相临两端头，拧卸缸28 正转，螺纹松开，拧卸缸28 复位，后夹紧缸27 松开，动力头马达21 反转直到两拉杆之间的螺纹完全松开。然后后夹紧缸27 夹紧，动力头马达21 反转，将第一根拉杆与动力头之间的螺纹连接松开，操作工取出第一根拉杆。

液压缸18 前行至最大行程处停止，动力头马达21 正转，动力头上阳螺纹与第二根拉杆的阴螺纹咬合上紧，动力头马达21 停止转动，前夹紧缸26 松开，液压缸18 退后至初始位置。重复上述动作。

2 液压系统可靠度计算

由文献［3］可知液压系统可靠性定义:在规定条件和规定时间内，液压设备无故障地完成规定功能的概率。而失效率λ(t)是指液压设备和液压元件工作到某时刻尚未失效的概率。通过长时间的工程实践和实验证明:在液压设备的正常运行时期，其失效率λ(t)是不随时间而改变的常数。则可靠度R(t)记为:

2.1 液压系统中各元件可靠度的计算

首先要确定各液压元件的平均失效率λ0，它们都是通过长期实验得出的数据，如表1所示。

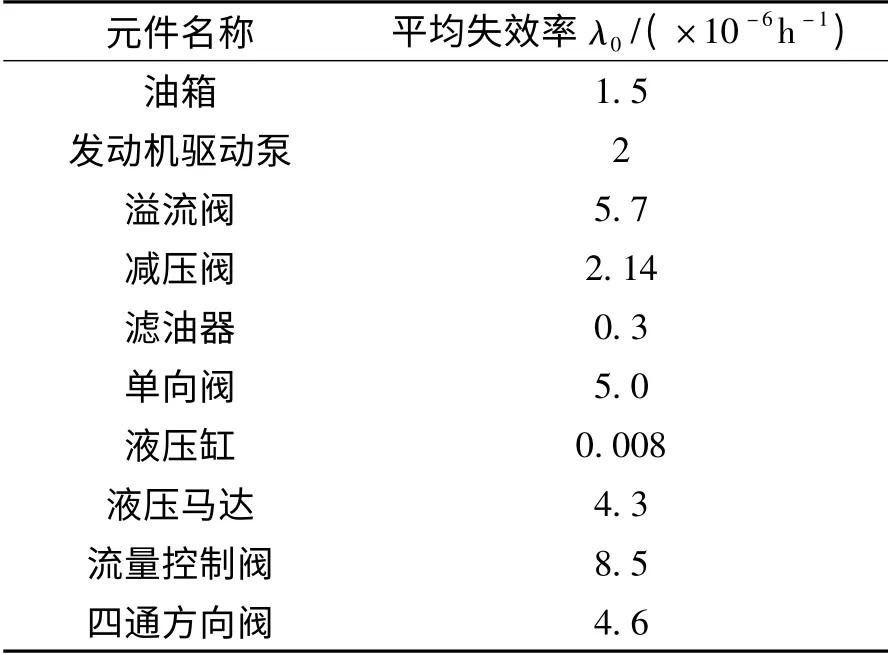
表1 液压元件在百万小时内的平均失效率

其次，要确定液压系统的使用环境，即环境系数K，如表2所示。

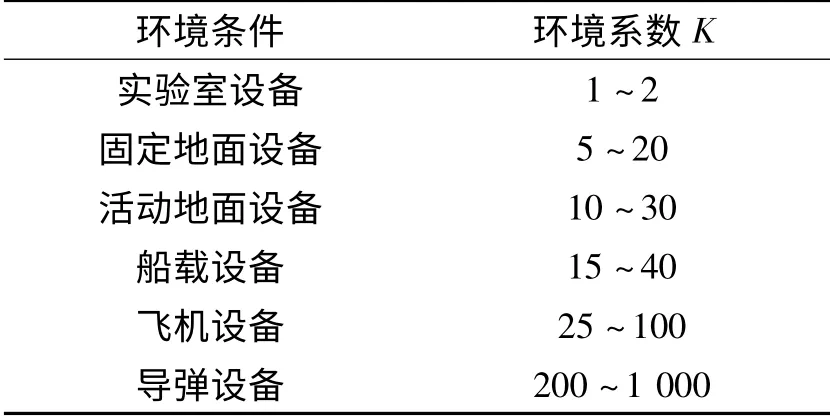
表2 液压系统环境系数K

最后，根据正常运行阶段中基于指数分布的液压系统的可靠度预测，即:

就可计算出液压元件的可靠度。

2.2 建立液压系统可靠性的逻辑模型

计算液压系统的可靠度不仅需要知道组成其系统的各个液压元件的可靠度，还要知道它们之间的组成形式。

一般而言，液压系统有4 种组成形式:串联系统;并联系统;混联系统;表决系统。通过分析图1可知:5 个子系统均为串联系统。根据液压裂管器液压系统的功能和各子系统的相互关系，可建立液压系统的可靠性逻辑模型，见图2。

2.3 液压裂管器液压系统可靠度计算

在串联液压系统中，组成系统的任何一个液压元件失效都会使整个液压系统失效。串联系统的可靠度为:

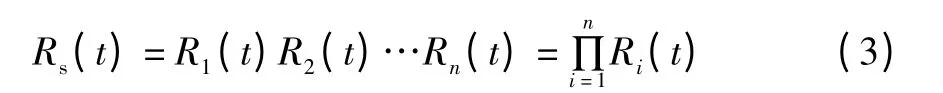
式中:Rs(t)为串联系统可靠度;

Ri(t)为液压元件可靠度。

图2 液压裂管器液压系统逻辑模型

将公式(2)代入公式(3)，并整理得:即串联系统的失效率λs为组成系统各液压元件失效率λi之和。

假设液压裂管器每连续工作100 h 大修一次，环境系数设为K=10，则液压系统正常运行时，各个子系统的可靠度计算如下。

(1)主伸缩子系统

Rs(t)= exp［－(1.5 +0.3 +2 +5 +5.7 +8.5 +8.5+4.6 +0.008)×10－6×10 ×100］=exp［－36.108 ×1×10－3］=0.965

(2)前夹紧子系统

Rs(t)=exp［－(1.5 +0.3 +2 +5 +5.7 +4.6 +5+0.008)×10－6×10 ×100］= exp［－ 24.108 × 1 ×10－3］=0.976

(3)后夹紧子系统

Rs(t)= exp［－(1.5 +0.3 +2 +5 +5.7 +4.6 +5 +0.008)×10－6×10 ×100］= exp［－24.108 ×1 ×10－3］=0.976

(4)拧卸子系统

Rs(t)= exp［－(1.5 +0.3 +2 +5 +5.7 +4.6 +0.008)×10－6×10×100］=exp［－19.108 ×1 ×10－3］=0.981

(5)动力头旋转子系统

Rs(t)=exp［－(1.5 +0.3 +2 +5 +5.7 +2.14 +8.5 +4.6 +4.3)×10－6×10 ×100］=exp［－34.04 ×1 ×10－3］=0.967

由整机功能及液压系统的顺序动作分析，可知这5 个子系统看似并联，实际上是一个5-out-of-5 的表决系统，在工程实际中作为串联系统来计算。则液压裂管器液压系统的可靠度为:

Rs(t)=0.965 ×0.967 ×0.981 ×0.976 ×0.976 =0.872

上述计算结果表明，液压裂管器液压系统每连续工作100 h 大修一次，则其可靠度为0.872。

液压裂管器液压系统在不同工况(工作时间、工作环境)下的可靠度如表3所示。

表3 不同工况的可靠度

由表3 可得出结论:液压裂管器工作时间越长，工作环境越恶劣，液压系统的可靠度就越低。

3 可靠性分析

由液压裂管器液压系统的组成可看出:主伸缩子系统、前夹紧子系统、后夹紧子系统、拧卸子系统、动力头旋转子系统密切联系，任何一个子系统失效，都会导致整个液压系统的失效，从而导致液压裂管器不能正常工作。

为了提高液压系统的可靠性，降低维护成本，延长经济寿命，可以采取以下措施:

(1)在理论设计阶段，在满足系统功能的前提下，减少串联环节;

(2)选择质量有保证的液压元件。实践证明，液压元件的可靠性是影响液压系统可靠性的主要因素;

(3)在加工零件时，要努力提高其加工制造精度;

(4)装配时要保证一定的装配精度;

(5)在控制液压油污染方面采取有力的预防和控制措施;

(6)应按要求按时对液压系统进行必要的维护。

4 结束语

(1)评价一个液压系统的可靠性，应以一定的条件(工作环境、工作时间、工作强度)为前提，否则是没有实际意义的。一般而言，工程机械的可靠度应为0.6 ～1。

(2)液压系统可靠性的提高，应从理论设计、零件加工、产品装配、设备使用和维护等各个阶段来综合考虑。

【1】成大先.机械设计手册:第五卷［M］.5 版.北京:化学工业出版社，2008.

【2】湛从昌.液压可靠性与故障诊断［M］.2 版.北京:冶金工业出版社，2009.

【3】许耀铭.液压可靠性工程基础［M］.哈尔滨:哈尔滨工业大学出版社，1991.

【4】原思聪，裴喜永，刘波，等.基于ADAMS 的80T 液压裂管器液压系统建模与仿真分析［J］.机械设计与制造，2011(1):186－188.

【5】吕刚，谷立臣.泵式混凝土湿喷机液压系统可靠性分析与计算［J］.建筑机械，2003(11):73－76.

【6】张锦华，原思聪，林艳.液压换管机液压系统可靠性设计与动态仿真研究［J］.机床与液压，2011，39(7):56－57.