基于加权渐进插值的Loop细分曲面等距逼近

陈甜甜， 赵 罡

（北京航空航天大学机械工程及自动化学院，北京 100191）

基于加权渐进插值的Loop细分曲面等距逼近

陈甜甜， 赵 罡

（北京航空航天大学机械工程及自动化学院，北京 100191）

等距曲面在 CAD/CAM 领域有着重要的作用，由于细分曲面没有整体解析表达式，使得计算细分曲面等距比参数曲面更加困难。针对目前已有的两种等距面逼近算法进行了改进，利用加权渐进插值技术避免了传统细分等距逼近算法产生网格偏移的问题。此外，提出了针对边界等距处理方案，使得等距后的细分曲面在内部和边界都均匀等距。该方法无需求解线性方程组，具有全局和局部特性，能够处理闭网格和开网格，为Loop细分曲面数控加工奠定了良好的基础算法。最后给出的实例验证了算法的有效性。

等距；Loop细分曲面；渐进插值；逼近

曲面等距在快速成型、数控加工、机器人运动干涉的避免以及带厚度薄片实体（如汽车车身、箱包等）的计算机辅助几何设计中有着广泛的应用，尤其在数控加工刀具轨迹的生成方面，通过将等距面与一系列平面相交可以产生无干涉的刀具轨迹[1]。可见，曲面等距是CAD/CAM领域最重要的几何操作之一。

近十几年来，随着细分理论基础的不断加深与拓展，细分造型技术已经成为三维模型造型中非常重要的一类技术。细分曲面是初始网格通过对细分规则不断迭代生成光滑曲面的造型方法，结合了多边形造型和参数曲面造型的优点，能够将光滑的设计模型和离散的加工模型整合与统一模型中[2]。除保留了传统NURBS曲面保凸性、局部可调等良好性质外，其优于NURBS曲面的拓扑任意性和一致性使得细分曲面逐渐受到工业造型和数控加工领域的广泛关注。但是细分曲面这一非常具有潜力的造型技术还未真正应用于工程领域，究其原因，一是细分曲面没有显式的数学表达公式；二是细分曲面没有完善的配套几何工具，例如等距和相交，这就限制了细分曲面在CAD/CAM中的应用。

目前，针对细分曲面等距逼近的研究还较少，主要有反算法和直接法。Kurgan和Suzuki[3]最先提出了基于 Catmull-Clark细分曲面的等距逼近算法。丁俊勇[4]等人在该算法基础上提出了改进的高斯雅克比迭代的Loop细分曲面等距逼近算法。白杰[5]重点研究了带折痕的 Loop细分曲面等距问题。上述细分等距算法被称为反算法。Loop细分反算法的主要思想是首先将初始网格细分1～2次，以确保每一个面都是三角形且至多包含一个奇点；然后将细分曲面的等距转化为细分曲面控制网格的等距，通过解全局线性方程组来得到等距后的细分曲面控制顶点。但是，当控制网格的数据量较大时，全局操作的反算法计算速度慢，灵活度小。此外，由于Loop细分的收缩性，导致了细分后的控制网格与初始网格的偏移。如图1所示，Loop细分一次后的网格与初始网格相比有明显的收缩，每次细分之后，细分的边长将会是原来的一半左右，这会造成被等距的网格与初始网格的偏移。

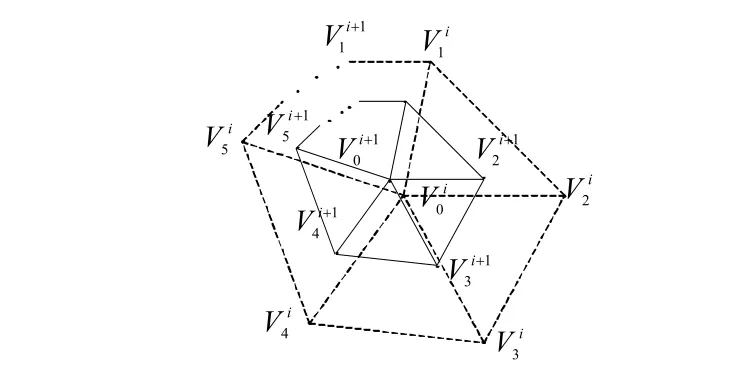
图1 Loop细分一次前后网格对比[6]

另一种曲面等距逼近方法是直接法。主要思想是根据逼近误差计算出细分次数，控制网格经细分后直接计算出逼近的等距面[7]。从等距面的生成步骤看直接法更加简单，省去了反算法求解方程组的步骤，计算速度快。但是，随着细分次数的增加，控制顶点越来越逼近极限曲面的同时，控制顶点与初始网格顶点的偏移会越来越大。上述两种等距逼近算法都会造成初始网格与极限曲面的偏移，从而导致等距面的偏移。在边界问题上，两类算法都未给出具体的边界处理方法，对于开网格等距逼近效果不理想。

由于三角形网格模型在实际应用中最为常用，四边形网格也需要划分为三角面片进行处理，故针对C2连续的Loop细分曲面，提出了一种不需解线性方程组且能避免与初始网格偏移的 Loop细分曲面等距逼近算法。针对曲面等距中的边界保持、误差控制和自交问题进行了深入分析，此等距逼近算法同样适用于其他细分模式。

1 加权渐进插值

1.1 Loop细分曲面渐进插值

不论是反算法还是直接法都存在细分后的控制网格与初始网格偏移的问题。为了避免与初始网格的偏移，利用渐进插值技术，通过不断迭代修正控制顶点得到一系列控制网格，其极限曲面插值于初始网格。

具体地，给定一个3D三角网格M=M0，通过渐进插值迭代方法来生成一个光滑的Loop细分曲面S插值于初始网格M0的所有控制顶点。对于M0上的每一个顶点V0，闭合网格Loop细分渐进插值算法具体步骤如下：

Step 1 利用 Loop细分曲面极限位置公式(1)，计算V0在其细分曲面S0上的极限位置

Step 2 计算V0与极限位置之间的距离添加距离D0进行修正得到新的顶点和新的三角网格M1；

Step 3 如果三角网格M1对应的细分曲面S1与初始网格M0之间的距离小于给定的误差，则停止迭代，否则进入Step2，即对 V1添加距离D1进行修正；

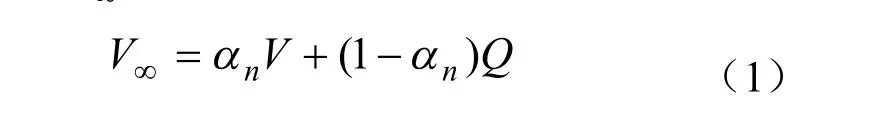
其中

Qi是顶点V的1-领域点。由此看出，迭代渐进插值算法是局部过程，故可以处理任意大小的网格。需要指出的是，虽然这个插值过程是不断迭代得到，但也可以不需要重复迭代k次，直接跳过中间的计算得到三角网格 Mk+1。只需限制M0与细分曲面 Sk+1之间的距离小于给定的误差即可。

1.1.1 最优权因子的选取

既然渐进插值算法是一个局部修正的迭代过程，那么需考虑其收敛速度。通过对控制顶点进行加权迭代，即能够达到控制渐进插值收敛速度的目的。对于每一个权因子其极限网格都是相同的，文献[8]讨论了使得迭代过程收敛速度最快的权因子。对于大部分模型，迭代过程收敛速度最快的权因子分布在，方便起见本文取最优权因子。结合实例模型，Loop细分曲面渐进插值权因子与迭代次数的关系如表 1所示，加权的Loop渐进插值算法只需更少的迭代次数，便能够得到大致相同的误差精度。

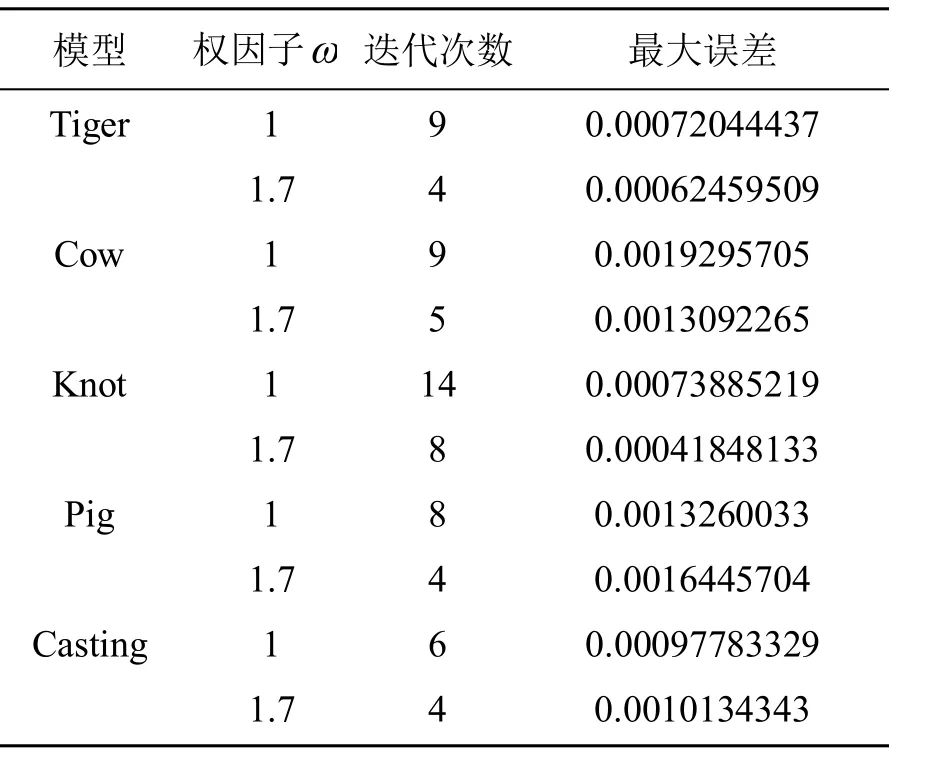
表1 权因子ω与渐进插值迭代次数之间的关系

1.2 边界处理

对于开网格，Loop细分渐进插值算法类似于闭网格，主要需要考虑的是边界的处理。就Loop细分而言，边界顶点与内部顶点具有不同的细分模版。使用如下图1的边界模版，从而保证产生的光滑曲面在边界处达到 C1连续。其中圆点代表规则点，即边界顶点度为4如图2(a)；三角形代表边界奇点，即边界顶点度不为4，如图2(b)～(d)。

图2 Loop细分边界模版（圆代表规则点，三角形代表奇点）

由1.1节可知，Loop细分渐进插值最重要的环节是计算顶点极限位置，边界顶点可通过与周围邻顶点的线性组合得到该点极限位置，这些顶点或者是规则点或者是奇点，根据不同类型的顶点就能够得到不同边界顶点的极限位置，六种不同的边界顶点极限位置模版如图3所示。若边界顶点为规则顶点，则极限位置计算公式如图3(a)～(c)；若边界顶点为奇点，则极限位置计算公式如图3(d)～图3(f)。

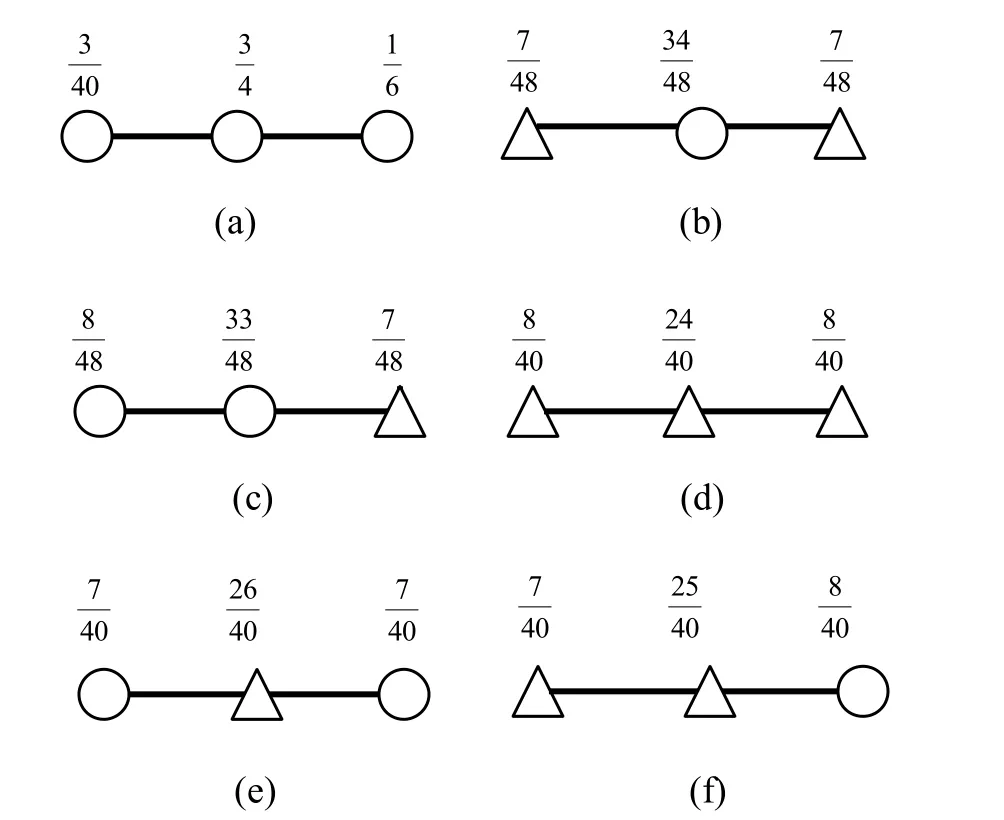
图3 边界顶点极限位置模版

需要注意的是，Loop细分渐进插值边界顶点细分计算只需要边界顶点的参与，所以渐进插值对于边界的处理可以首先计算边界的渐进插值。一旦边界处理完毕后，就可以进行内部顶点的渐进插值算法，而无需边界顶点任何的改变。最终得到的网格将插值于边界顶点和内部顶点。不论边界如何不连续，都可以采用局部几何运算同时计算边界插值，从而避免了求解多个线性方程组。对于边界顶点运用渐进插值技术其收敛性也是可以证明的[8]。

2 Loop细分曲面等距逼近

2.1 Loop细分曲面极限位置法矢

利用上述加权渐进插值算法可以得到无偏移的插值于初始网格的Loop细分曲面。给定距离d，沿着法矢方向等距就可以得到最终的细分曲面等距逼近。

在光滑顶点（规则点）处可以利用加权平均法向量得到该光滑顶点的法矢。对于尖锐特征（奇点）处，如果按照加权平均法计算法矢就会产生较大的误差，故需要特殊处理。利用多法向量法[9]计算奇点处的法矢，即通过将奇顶点分裂为多个顶点来求得新的法矢，如图4所示,将顶点V分裂为V1和V2。

图4 利用顶点分裂求奇异顶点法矢

2.2 自相交处理

细分曲面等距后，可能会引起两种类型的自交：一类为局部自交，是指凹陷处的局部曲率半径小于等距值，导致等距曲面相交；另一类为全局自交，是指曲面片分离间隙小于等距值，导致等距曲面相交。利用Loop细分模式的凸包性，通过检测等距后的三角控制网格是否自交，可以快速判别等距曲面是否自交。3D模型直接检测和去除等距面自相交较困难，通过与一系列平面相交生成二维刀具轨迹后更容易处理。去除刀具轨迹中的自相交环得到无干涉的刀具轨迹[10]。

3 实验结果与讨论

本文是结合OpenGL在Visual C++6.0下实现该算法。实验环境是基于Windows XP操作系统，奔腾IV3.0GHZ处理器，1GB内存，采用的数据结构是半边数据结构。

为验证上述算法的有效性，对大量模型进行了检测，具体参数信息如表2所示。利用最优权因子加速渐进插值的收敛速度，减少了的迭代次数，提高了计算效率。下面给出几个模型实例。图5是两个闭合网格模型pig模型和knot模型。根据1.1节的步骤，分别迭代修正控制顶点4次和8次生成Loop细分曲面图5(b)和图5(e)；光滑且保留了初始网格的细节特征的等距曲面见图5(c)和图5(f)。图6(a)是带有内环的闭网格casting实体图，无偏移的插值于初始网格的Loop细分曲面如图6(b)；按照2.1节求出等距网格顶点的外法矢方向等距后得到图6(c)，可以看出内环处均匀等距。

表2 基于WPI的Loop细分曲面（ω=1.7）

对于开网格face模型见图7(a)，首先利用1.2节对边界进行处理，然后按照1.1节步骤处理内部顶点。为了更加直观比较，本文给出face模型Loop细分曲面等距逼近的正面图和侧面图。图7(a)是初始网格实体图的正面图和侧面图。图7(d)是利用文献[7]中的算法生成的Loop细分曲面等距逼近。很明显，从正面图和侧面图都可以看出在边界处有凹凸不平，边界处与初始网格相比有明显的收缩。而利用本文算法生成的Loop细分曲面等距逼近能够统一处理开网格和闭网格，无论在内部和还是边界处等距效果都较好，见图7(c)。

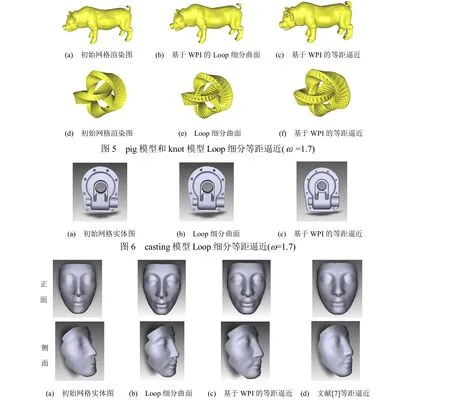
图7 face模型Loop细分等距逼近(ω=1.7)

4 结 论

本文提出一种简单新颖的Loop细分曲面等距逼近算法。利用最优权因子不断迭代修正控制顶点，得到无偏移的插值于初始网格的Loop 细分曲面。等距后的细分曲面与初始网格具有相同的拓扑结构，特别是边界处等距效果较好。与传统细分曲面等距算法相比，该方法避免求解线性方程组，能够统一处理开网格和闭网格等距逼近。未来的工作将对等距中的自相交问题进一步研究，尤其是凹陷处局部自相交的检测和去除。

[1] Qu X Z, Brent S. A 3D surface offset method for STL-format models [J]. Rapid Prototyping Journal, 2003, 9(3): 133-141.

[2] Lu C J, Ting K L. Subdivision surface-based finish machining [J]. International Journal of Production Research, 2006, 44(12,15): 2445-2463.

[3] Kurgano J, Suzuki H, Kimura F. Generation of NC tool path for subdivision surfaces[C]. Proceedings of CAD/Graphics. China, 2001: 676-682.

[4] 丁俊勇, 胡事民, 周登文. Loop细分曲面的等距曲面的逼近[J]. 计算机学报, 2003, 26(7): 789-796.

[5] 白 杰, 赵 罡, 姚福生. 带折痕的Loop细分曲面等距面处理算法[J]. 计算机辅助设计与图形学学报, 2008, 20(10): 1261-1265.

[6] 张景峤. 细分曲面生成及其在曲面造型中的应用[D].浙江: 浙江大学, 2003.

[7] 王占东. 细分曲面关键技术研究[D]. 南京: 南京航空航天大学机械学院, 2003.

[8] Cheng F H, Fan F T, Lai S H. Loop subdivision surface based progressive interpolation [J]. Journal of Computer Science and Technology, 2009, 24(1): 39-46.

[9] Deng C Y, Ma W Y. Weighted progressive interpolation of Loop subdivision surfaces [J]. Computer Aided Design, 2012, 44(5): 424-431.

[10] Kim S J, Yang M Y. Triangular mesh offset for generalized cutter [J]. Computer Aided Design, 2005, 37(10): 999-1014.

[11] Jung W, Kim D S, Choi B K. Self-intersection removal in triangular mesh offsetting [J] . Computer Aided Design, 2004, 1(1-4): 477-484.

Offset Approximation of Loop Subdivision Surface Based on Weighted Progressive Interpolation

Chen Tiantian, Zhao Gang
( College of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China )

Offset plays an important role in the field of CAD/CAM. The offset approximation computation is more difficult for subdivision surfaces than parametric surfaces because subdivision surfaces have no analytical expression. The proposed approach is an improvement of two existed subdivision surface offset algorithms. Using the weighted progressive interpolation (WPI) method avoids the mesh deviation caused by the traditional methods. The boundary offset treatment is presented to obtain the uniform offset mesh. The proposed method avoids solving a linear equation system and has the advantages of both local and global methods. The method can be used to deal with either closed or open meshes. Offset approximation is an important operator to the applications of Loop subdivision surfaces in NC machining. Some typical examples are illustrated to demonstrate the efficiency of the proposed approach in the end.

offset; Loop subdivision surface; progressive interpolation; approximation

TP 391

A

2095-302X (2013)05-0066-05

2013-05-03；定稿日期：2013-06-08

国家自然科学基金(61170198)

陈甜甜（1982-），女，上海人，博士，主要研究方向为CAD/CAM。E-mail：candy_ctt@163.com

赵 罡（1972-），男，河北文安人，教授，博士生导师，主要方向为CAD/CAM，几何造型，虚拟现实。Email：zhaog@buaa.edu.cn