带约束的B样条曲线曲面延伸技术
徐 进
(浙江科技学院机械与汽车工程学院,浙江 杭州 310023)
带约束的B样条曲线曲面延伸技术
徐 进
(浙江科技学院机械与汽车工程学院,浙江 杭州 310023)
论文提出了一种带光滑有序点列约束的 B样条曲线延伸方法。该算法能够根据约束点列的情况对曲线延伸部分所对应的节点值进行优化,通过插值尽量少的约束点,使得延伸曲线与约束点列之间的最大距离小于预先给定的误差值,并且延伸曲线与原始曲线之间自然达到最大阶连续。该方法也同样适用于带曲线约束的 B样条曲面延伸。实例表明,所提出的算法是可行且有效的。
B样条;延伸;有序点列约束;节点修正
在几何建模的过程中,许多针对B样条曲线的算法和操作被广泛地研究和使用,如曲线的拟合(包括插值和逼近)、光顺、组合、变形等。在许多CAD系统中,B样条曲线的延伸也是常用的算法之一,通常是将曲线延伸到某一个目标点或是延伸一个特定的距离。为了补充曲线曲面构造特征的不足。需要对曲线曲面进行操作处理(如裁剪和延伸)。它可用于不相交的曲面求交及曲面在圆角的过渡。目前,曲线延伸普遍采用的方法是在B样条曲线延伸端的端点和目标点之间构造一条Bézier曲线,使得Bézier曲线与原B样条曲线在连接处达到G1连续,然后将两段曲线组合成一条曲线,并用B样条进行表达。周元峰等[1]通过极小化目标函数实现了G2连续约束下三次Bezier曲线向一点的延伸,并且曲线的形状可以调整,但是该方法并不适用于B样条。余正生等[2]详细推导了非均匀有理B样条(NURBS)曲线曲面延伸且满足切平面连续和曲率连续的数学表达式;Shetty等[3]提出了一种既直接又实用的方法对有理B样条曲线和曲面进行延伸,且在延伸过程中不改变原曲线或曲面的形状和参数值。然而,采用这种方法得到的延伸曲线的节点矢量在内部存在多重节点的情况,因此,在通用CAD系统中并不被广泛采用。Chivate等[4]利用曲线和曲面在延伸端的一阶导数信息将曲线和曲面延伸至定义域之外,但是,由于在延伸过程中改变了原曲线和曲面的形状,因此,在很大程度上限制了该方法的应用。Hu等[5]利用B样条曲线的端点松弛算法和de Boor递推公式将B样条曲线延伸至一个或多个目标点,曲线延伸部分与原曲线在连接处达到最大的连续阶(即连续阶等于原B样条曲线的次数减1)。但是,由该方法得到的延伸曲线形状是唯一的,因此,常常不能满足要求。
本文提出了一种带光滑有序点列约束的 B样条曲线延伸算法。所有约束点被划分为两大类:插值点集和逼近点集。首先,将有序约束点列中的最末点作为唯一的插值点加入到插值点集中,将其余点加入到逼近点集中,并在算法每次迭代过程中增加一个插值点,相应地减少一个逼近点。对于给定数目的插值点,运用B样条曲线端点松弛算法和de Boor递推算法的逆过程将原B样条曲线进行延伸,使得延伸曲线插值于插值点集内的每一个点。然后通过求解一个非线性优化问题对曲线延伸部分所对应的节点矢量值进行优化,使得曲线延伸部分能够更加贴近逼近点集中的所有点。经过数次迭代后,最终使得延伸曲线在小于预先给定的容差值的前提下插值尽可能少的约束点。
1 B样条曲线端点松弛算法
在几何建模中,通常采用端点夹持型的B样条曲线来表示自由曲线模型。一条p次的端点夹持型B样条曲线可表示为:

其中Pi为曲线的控制顶点,为定义在规范化非均匀节点矢量上的p次B样条基函数。若是任意一组大于 1的递增实数序列,即则可以为新的节点矢量将曲线 P(u)在末端点处进行松弛化处理。将端点松弛化后的曲线记为:


其中:

2 带光滑有序点列约束的B样条曲线延伸
2.1 插值点数目一定时的B样条曲线延伸
即使约束点列较光滑,在曲线延伸过程中如果要求延伸曲线插值每一个约束点,可能会使得延伸曲线出现局部波动或扭曲现象,所以没有必要使得延伸曲线严格插值每一个约束点,其中一部分约束点只需要逼近即可。将光滑有序约束点列记为W={R1, R2,…, RM},若延伸曲线插值了其中t个约束点,则可将W分解为两个子集:插值点集和逼近点集 WA= W -WI,其中。如果赋予每一个插值点一个参数值si,并将si作为延伸后曲线节点矢量中的一个节点值,则延伸以后曲线的节点矢量将由 U0变为:且延伸后的曲线可表示为如下形式:

各插值点处的参数值 si可由下面的方法计算得到:

其中,||•||表示欧氏距离。

图1所示为B样条曲线的de Boor求值算法的计算过程,图2为相应的控制顶点递推示意图。从图1和图2可以看出,当未知时,整个计算过程中只有未知。如果令,运用de Boor求值公式(7)可以计算得到的值。类似地,当和已知时,可以计算得到的值。不断地往回递推计算,最终可以得到的值,此即为需要求的控制顶点

图1 B样条曲线的de Boor求值算法

图2 de Boor求值算法中控制顶点的递推过程
如果插值点的个数大于曲线P(u)的次数,即t>p,则在计算得到所有新的节点值si(i=1, 2…, t)之后,以
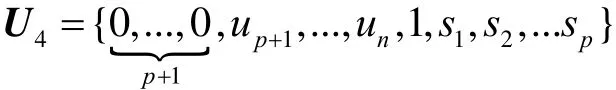
为新的节点矢量,将曲线P(u)在末端进行端点松弛化处理,延伸曲线控制顶点的计算方法与前述相同。
2.2 节点修正
节点矢量的选择对B样条曲线的形状起着非常重要的作用,使用B样条的关键之一就是是否能确定好的节点矢量[7]。不合理的节点矢量会使B样条曲线的形状发生波动或扭曲,从而使得其形状不能满足要求。对于曲线的插值,节点矢量的配置相对比较容易直接。然而,对于曲线逼近来说,要确定节点矢量的位置和数量则是相当困难的一件事情[8]。
在带光滑有序点列约束的B样条曲线延伸过程中,同时存在着插值和逼近。一旦插值点被选定之后,新节点的数量和位置都已经确定,但是,如何确定这些节点的值仍是一个相当棘手的问题。通常情况下,由式(6)计算得到的新的节点值并不是最佳值,因为该计算方法并没有把逼近点考虑进去。因此,若以此节点矢量将原曲线进行延伸之后,虽然延伸曲线能够插值所有的插值点,但是曲线的延伸部分可能偏离逼近点较大的距离,如图3(b)所示,甚至可能会发生扭曲的现象,如图3(e)所示。这使得延伸曲线无法满足误差和光顺性要求,而且还会影响到算法的效率和稳定性。众所周知,一条p次的B样条曲线的形状由它的控制顶点和节点矢量唯一确定。由式(3)、式(4)和式(7)可知,与曲线延伸部分对应的控制顶点由延伸后曲线的节点矢量和原曲线端点松弛化后的部分控制顶点共同确定。因此,可以将新的节点看作变量并对其进行修正来控制延伸部分曲线的形状。为讨论方便,本文只考虑p=3时的情形,当曲线的次数为其它值时情况是类似的。

图3 有无节点修正对带点列约束的B-样条曲线延伸结果的影响
2.2.1 单个插值点的情况
如果只有一个插值点RM,则延伸后曲线Q(u)的节点矢量为:U5={0,0,0,0,u4,...,un,1,s1, s1, s1, s1},其中,s1由式(6)计算求得,此时控制顶点与点RM重合。由式(3)和式(4)可知,当s1发生改变时,控制顶点中只有和会受到影响而发生相应地改变,需要重新计算其位置,而其余的控制顶点均保持不变。在只有一个插值点的情况下,曲线延伸部分的形状完全由s1决定,因此,如果能用一个更优的节点值w1来替换s1便可以改善曲线延伸部分的形状。所以,特别地将w1表示为如下形式:

其中k1>0称作修正系数。以U5为新的节点矢量用上节的方法对原曲线P(u)进行延伸,并将曲线延伸部分的弧长记为S1,若将所有约束点的弦长总和记为C1,即:

则有:

由于约束点的形状可能千差万别,所以,试图找到一个通用的计算公式来计算k1的值是不现实的。所以,宜采用迭代的方法来近似计算最优的k1值,从而得到近似最优的节点值w1。
以U5为新的节点矢量对原曲线P(u)进行延伸后,如果约束点到延伸曲线Q(u)的最大距离大于给定的容差E,则令:


2.2.2 多个插值点的情况
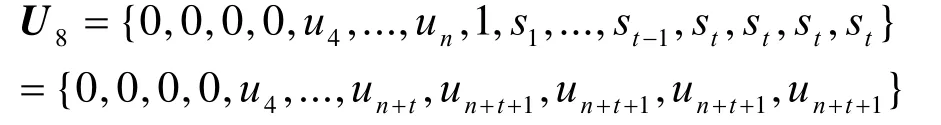



则最优化问题式(14)可转换为如下形式:

最优化问题式(15)为带线性约束的非线性最优化问题的标准形式,可采用投影梯度法[9]来求解该问题。将作为问题式(15)的初始可行解,由于初始可行解通常距离最优解较近,并且在带光滑点列约束的曲线延伸过程中插值点的个数通常不多,所以,该求解过程通常能在较少的迭代次数之后终止。在本文作者所测试的例子中,求解过程都能够收敛。
2.3 算法描述
给定一条光滑的 B样条曲线以及一光滑有序约束点列,首先,以约束点列中的最末点作为唯一的插值点将B样条曲线进行延伸。计算约束点列中各点到延伸曲线的距离,如果最大距离大于预先给定的阈值,则将点列中与延伸曲线距离最大的点作为下一个插值点加入到插值点集中,并以新的插值点集将原 B样条曲线重新进行延伸。重复这一过程,不断地加入新的插值点,直到最大距离小于给定的阈值或者所有的约束点都被选为插值点为止。带光滑点列约束的B样条曲线延伸的算法流程如图4所示。
图5给出了一些带光滑点列约束的曲线延伸的例子,并用黑点标出的约束点为最终的插值点。从误差的角度出发,当插值点的个数逐渐增多时,延伸曲线与约束点列之间的最大距离是不断减小的。但是,随着插值点个数不断增多,延伸曲线的形状将会出现波动或扭曲的现象,而且也会影响到算法效率。但对于光滑的约束点列,通常只需插值少数几个点便可使得延伸后的曲线满足误差要求。
3 带曲线约束的B样条曲面延伸
带光滑点列约束的 B样条曲线延伸算法可以推广到带B样条曲线列约束的B样条曲面延伸。一张p×q次的B样条曲面可表示为如下形式:

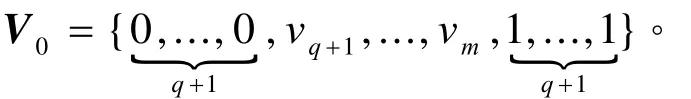
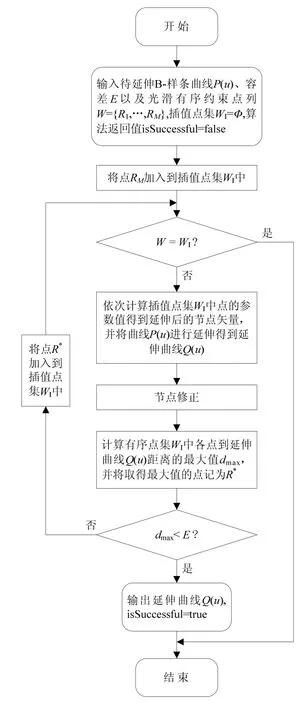
图4 带光滑有序点列约束的B样条曲线延伸算法流程图

图5 带点列约束的三次B-样条曲线延伸实例
为方便起见,本文只讨论曲面S(u, v)沿v向的约束延伸问题,沿u向的延伸完全类似。设B样条曲线约束为Tl(u)(l=1,2,..., M),不失一般性,这里假设所有约束曲线的次数均为p,并且节点矢量都为U0(如若不相同,可以采用升阶算法和节点插入算法使得所有约束曲线的次数和节点矢量相同)。将曲线 Tl(u)的控制顶点记为,约束曲线中的插值曲线集记为,与其相对应的v向参数值记为{s1,s2,...,st},并将{s1,s2,...,st}作为延伸后曲面的v向节点值,则曲面S(u,v)沿v向延伸后的新节点矢量将变成:
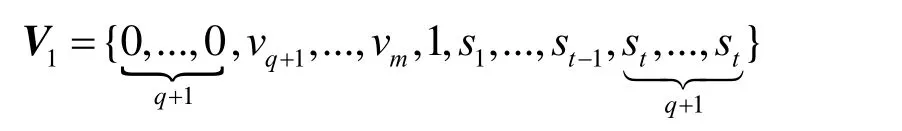
将曲面S(u,v)沿v向在边界S(u,1)处进行松弛化之前,必须先计算{s1,s2,...,st}的值。这里,仍采用式(6)来计算si的值,但此时需用两条B样条曲线之间的“距离”来取代两点之间的距离。将相邻的两条约束曲线之间的“距离”定义为:



图6 带曲线约束的B样条曲面延伸实例
4 结 论
本文提出了一种带光滑有序点列约束的 B样条曲线延伸算法,并将该算法推广到了带B样条曲线约束的B样条曲面延伸。运用该算法得到的延伸曲线与原曲线之间能够自然达到所允许的最高阶连续,且原曲线在整个延伸过程中始终保持不变。但是当约束点列不够光滑或存在波动时,所需的插值点个数会增多,从而影响到该算法的效率以及延伸曲线的品质,下一步将对此进行重点研究。
[1] 周元峰, 张彩明. G2连续约束下三次 Bézier曲线的延拓[J]. 计算机辅助设计与图形学学报, 2005, 17(3): 425-430.
[2] 余正生, 雷 毅. NURBS曲线曲面延伸[J]. 工程图学学报, 1997, 18(1): 7-18.
[3] Shetty S, White P R. Curvature-continuous extensions for rational B-spline curves and surfaces [J]. Computer-Aided Design, 1991, 23(7): 484-491.
[4] Chivate P N, Puntambekar N V, Jablokow A G. Extending surfaces for reverse engineering solid model generation [J]. Computers in Industry, 1999, 38(3): 285-294.
[5] Hu Shimin, Tai Chiewlan, Zhang Songhai. An extension algorithm for B-splines by curve unclamping [J]. Computer-Aided Design, 2002, 34(5): 415-419.
[6] Piegl L A, Tiller W. The NURBS book [M]. New York: Springer-Verlag, 1997: 572-580.
[7] Farin G. Curves and surfaces for CAGD [M]. San Francisco: Morgan Kaufmann, 2002
[8] Li Weishi, Xu Shuhong, Zhao Gang, et al. Adaptive knot placement in B-spline curve approximation [J]. Computer-Aided Design, 2005, 37: 791-797.
[9] Hadley G. Nonlinear and Dynamic Programming [M]. Massachusetts: Addison-Wesley Publishing Company, Inc, 1964: 315-323.
B-spline Curves and Surfaces Extension with Constraints
Xu Jin
( School of Mechanical and Automative Engineering, Zhejiang University of Science and Technology, Hangzhou Zhejiang 310023, China )
An algorithm for extending B-spline curves with a sequence of ordered points constraint is presented based on the curve unclamping algorithm. The most important feature of this algorithm is the ability to optimize the knots of the extended curve segment according to the ordered points. Thus, with minimum number of interpolation points, the maximum deviation of the extended curve segment from the ordered points is less than the given tolerance. The extended curve segment connects to the original curve with maximum continuity intrinsically. Further more, this algorithm can be applied to the extension of B-spline surfaces with the constraints of a sequence of B-spline curves. Several experimental results have shown the validity and applicability of the proposed algorithm.
B-spline; extension; ordered points constraints; knots modification
TP 391
A
2095-302X (2013)03-0036-07
2012-06-23;定稿日期:2012-09-24
浙江省教育厅资助项目(Y201119634);浙江省自然科学基金资助项目(LQ13E050015)
徐 进(1981-),男,江西上饶人,讲师,博士,主要研究方向为逆向工程、CAD、CAGD。E-mail:xujin206@126.com

