后置处理中平面轮廓拐角加工程序自动生成技术

饶有福， 郑国磊， 陈 俊， 杜宝瑞， 初宏震

（1. 北京航空航天大学机械工程及自动化学院，北京 100191；2. 沈阳飞机工业集团有限公司，辽宁 沈阳 110034）

后置处理中平面轮廓拐角加工程序自动生成技术

饶有福1， 郑国磊1， 陈 俊1， 杜宝瑞2， 初宏震2

（1. 北京航空航天大学机械工程及自动化学院，北京 100191；2. 沈阳飞机工业集团有限公司，辽宁 沈阳 110034）

为解决早期数控程序中没有考虑拐角加工问题，本文提出了围绕NC代码识别拐角并自动生成拐角加工数控程序算法，以满足产品升级与加工高要求之需，进一步确保数控加工安全与零件表面质量。为实现拐角识别，首先总结归纳常见数控代码结构；其次还原NC代码的几何形态并采用线链表示，计算线链走向、线链边之切矢；将拐角分为点式拐角与圆弧式拐角两大类型，综合拐角的离散结构与线链的封闭性，给出了拐角的识别原理与相应准则。拐角加工按分层铣削加工，从刀具轴向上减少刀具在拐角位置处加工瞬时的切削量；各层拐角加工刀轨由进刀、切入、拐角加工、切出与退刀五段组成；层间刀轨采用进退刀连接线衔接。最后用实例验证了该算法的正确性。

数控加工；拐角加工；NC代码；后置处理

在数控加工中，拐角(Corner)位置是一非常特殊区域。经加工实践证明，在该区域内，若刀轨安排不合理，很可能因刀具在瞬时切削量过大，使得刀具崩裂；或因瞬时切削量不均，刀具颤动，使得工件表面质量不佳。前者是生产安全问题，后者是工艺要求问题。然而这两个问题在加工中均应首要重点考虑，在航空企业内尤为突出。

围绕拐角区域开展数控刀轨生成、优化及加工方法等研究成果较为丰富。如针对拐角，有专门插铣操作[12]，并在较主流的 CAM 软件，如CATIA、UG及PowerMill等均有实现。为实现较优切削轨迹，在拐角处，分别提出了：

1） 在拐角处采用双圆弧[3]与类似碗状环形[4]铣削刀轨，保证切削过程中刀轨光滑过渡；

2） 以仿真分析为手段，在保证切削力恒定条件下，通过改变刀具中心坐标与铣削参数，实现拐角加工过程优化方法[5]；

3） 以实验为手段，研究在拐角处切削参数、切削力模型及两者间关系，在此基础上，适当调整切削参数以达到控制切削力与加工表面质量的目的[6-8]。

上述各拐角加工与优化方法均在NC代码生成前完成。而目前尚未见到专门针对NC代码开展拐角区域识别与拐角加工程序自动生成的研究。但针对NC代码开展拐角区域识别又是非常必要，主要体现在以下3个方面：

1） 早期未开展拐角加工的数控程序在拐角处已经无法满足当前日益提高的表面质量要求，甚至出现刀具崩裂。这主要是因为拐角加工研究起步较晚，早期数控程序内尚无开展拐角加工。

2） 大型零件，如航空结构件，拐角位置较多，专门在此位置开展拐角加工程序编制，耗费时间非常长，多则有3～4天。

3） 早期NC代码较多无三维数模，无法采用上述各拐角加工方法生成拐角加工程序。另外，拐角加工一般为平面加工，其加工导引元为平面曲线，因此，本文重点研究平面曲线的拐角加工。

针对需求，以 NC代码为研究对象，读取NC代码，还原刀轨路径，识别拐角位置；按分层加工法，并采用直线与圆弧相切加工方式，自动构建NC代码，实现拐角加工。该分层方法从刀轴方向上减少刀具瞬时切削量，保证在拐角位置处切削量减少，可减少刀具颤动，最终保障刀具在拐角位置处铣削安全与拐角处表面质量，最后结合实例开展分析和验证。

1 拐角识别与加工

为实现NC代码内拐角识别，首先需要熟知NC代码结构与关键指令。在此基础上还原加工轨迹线，识别拐角。

1.1 代码结构与关键指令

经生产实践表明，常见数控加工系统NC代码由程序号、程序段和其他符号组成。其中：

1） 程序号 加工程序之始，每数控系统都有自己定义的程序号，如采用%，并采用%结束；也以M02或M30表示程序结束。

2） 程序段 除程序号与注释行之外的每一行语句称为一个程序段。每程序段由一或多个指令构成，它组成了完成数控机床所需的某一特定动作的指令；由若干程序段组成全部加工程序。程序段结构一般为：

N G X Y Z F S T M

其中：

1） N为语句号字，N后为阿拉伯数字，即程序段号的编号，如N010，表示第10号程序段。

2） G为准备功能字，即特殊功能字符，如G90或G91分别表示按绝对坐标方式或增量坐标方式编程，该标识直接限定了坐标计算方式，若是增量坐标，则下一点的坐标为前一点坐标加上相应增量；G1或G01表示直线插补，G2与G3为顺时针圆弧/圆与逆时针圆弧/圆插补(或用G02、G03表示)，视线沿着垂直于圆弧所在平面的坐标轴负方向观察，刀具插补方向为顺时针即为G02，相反则为G03；G00为快速点定位。

3） X，Y，Z为尺寸字，分别表示 x，y，z坐标，也可用U，V，W表示。对于圆弧插补，用R，R=，CR，CR=，B，B=等形式表示圆弧半径，圆弧半径标识具体形态由用户根据数控系统类型输入；圆心用I，J，K表示。对于同一类型的连续两段插补，若当前程序段插补X坐标被省略，则表示当前程序段的X坐标与上一程序段一致。

4） F为进给功能字。

5） S为主轴转速字。

6） T为刀具功能字。

7） M为辅助功能字。

各功能字间由连字符连接，连字符可为空格或“_”。

1.2 拐角分类与识别

NC代码一般为刀具中心点运动轨迹（简称为刀轨），顺序相邻且均存在直线或圆弧插补的两程序段（本研究暂只考虑由圆弧与直线拆补构成的切削代码，样条切削代码暂不计）的可分别提取坐标值得到点由点pts和pte可构成一条边e；依次计算各程序段点坐标，可顺序连接各e，则构成线链c(e1, e2,…, en)，则线链c可表示一段连续切削刀轨。依拐角处的拐角曲面f的理论圆弧a的半径R值与刀具半径r间大小关系可得以下两条准则，其中拐角结构如图所示：

准则1 当R≤r时，圆弧a在线链c上退化为一点；

准则2 当R>r时，圆弧a在线链c退化成半径为R-r的圆弧。

依据上述准则，分别有如下规定：

1） 若拐角圆弧a退化为刀轨上的一点，则该拐角称为点式拐角，记为

2） 若拐角圆弧a退化为刀轨上的一圆弧，则该拐角称为圆弧式拐角，记为

如表1，按照当前走刀方向V顺序连接各段刀轨，可得一线链c(e1, e2,…, en)，线链c可为封闭环也可为开环。若对线链c中圆弧采用起点至中点，中点至终点两段直线段表示，并用该两直线段替换c中的该段圆弧，则构成新的线链cp(e1, e2, …, em)，并称此两直线段为该圆弧的置换直线段，则下述定理必然成立：

定理1 若线链cp中存在拐角，则必然存在极值多边形。

证明：若不存在极值多边形，则线链cp各顺序边均共线，那么必然不存在拐角。这与定理的前提cp中存在拐角不相符，因此，该定理成立。

其中，极值多边形为将线链cp中各顶点按照x与y值进行排序，规定cp中坐标点为或者的顶点为极值点并按cp中前后之序顺序连接各构成多边形，该多边形的走向与线链走向一致，计算方法详见文献[9, 10]。依据该定理，以下推论则必成立：

推论1 线链c(e1, e2, …, en)与将圆弧采用置换直线段代替得到的线链cp(e1, e2,…, em)具有相同的走向，且均为极值多边形按右手定则得到的矢量V。并有c中各圆弧起点至终点走向与置换直线段e1至e2走向一致。

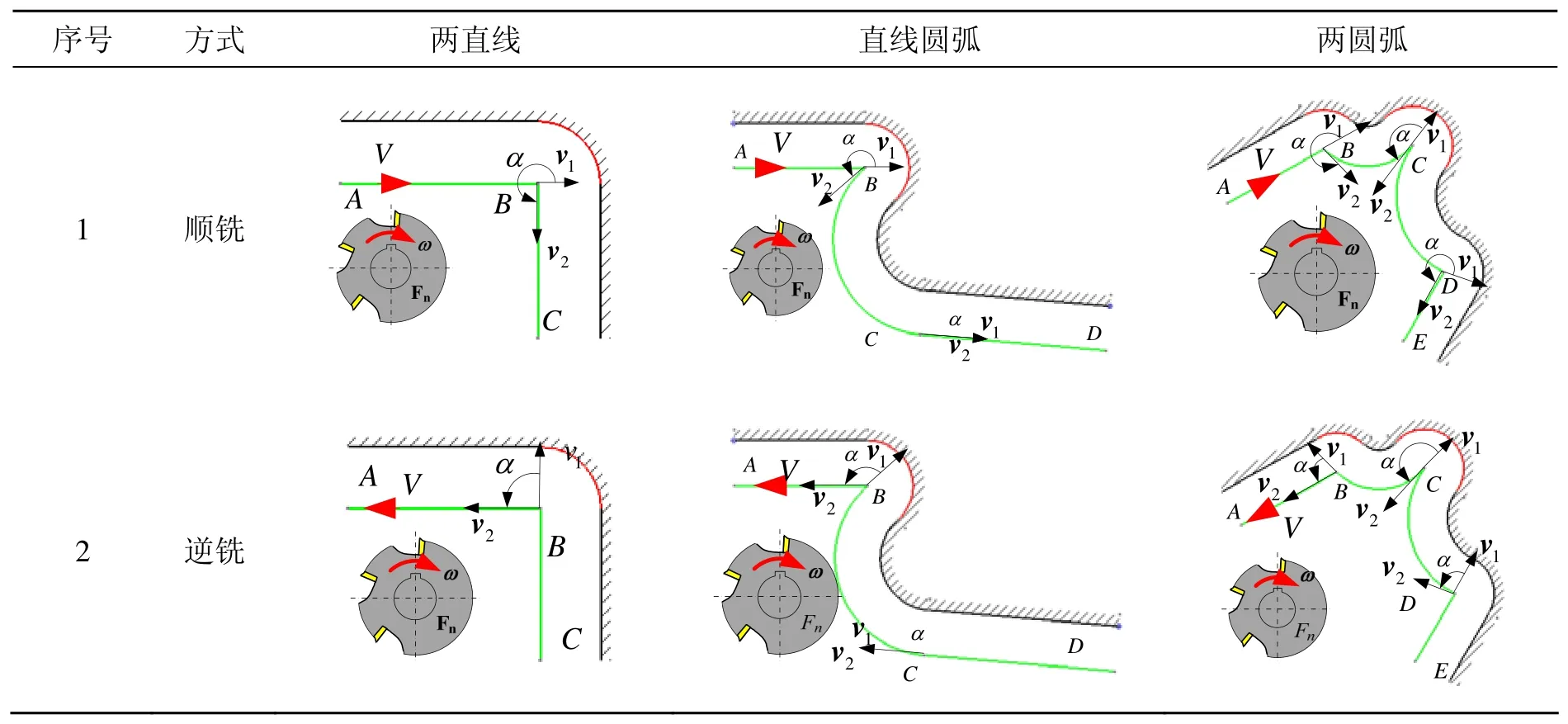
表1 相切型点式拐角分类实例

在本研究中，称极值多边形按照右手定则得到的矢量V为线链c(e1, e2, …, en)的走向方向，简称为线链c的方向。

推论2 沿着线链c(e1, e2, …, en)的方向V顺序走遍各边，若为顺铣时，则切削的零件表面始终在人之左侧；逆铣时，在人之右侧。

推论3 令当前加工坐标系Z轴正向Z+，线链c(e1,e2,…, en)的走向V且c封闭，则：

当满足以下条件之一：

（1） 逆铣且V与Z+同向；

（2） 顺铣且V与Z+反向，则c为加工轮廓而形成的刀轨环；

当满足以下条件之一：

（1） 逆铣且V与Z+反向；

（2） 顺铣且V与Z+同向，则c为加工凸台而形成的刀轨环。

方向为V的线链c(e1,e2,…,en) ，∀ ei∈c，则按方向V，ei在其起点pts与终点pte的切矢vs和ve计算依据分别为：

（1） ei为直线，则

（2）ei为圆弧，圆心为pto，则此时沿着加工坐标系Z轴负向Z-看去，按线链c之方向V，若圆弧走向为顺时针，则称ei为凹弧；逆时针走向，则ei为凸弧。此时圆弧走向计算方法为：取圆弧中点 ptm，计算矢量和，则圆弧走向v3=v1× v2，那么：若v3与Z-同向，则圆弧为凹弧；反之为凸弧。

实际上，当拐角角度较大时，此处残留余量一般不大，此时进行拐角加工没有意义。因此，设定当拐角张角α >θ 时，该拐角不加工，θ 为进行拐角加工的阈值。依据上述规定，和拐角识别判定原理分别如下。

Cpt拐角判定原理 线链c(e1,e2,…,en)走向V，端点pt前后关联的边分别为ei和，按V方向，ei和

在pt处切矢分别为v1和v2，按照右手螺旋法则，则v1至v2夹角为α，则若满足以下条件之一：

（1） 顺铣且0＜2π-α≤θ；

（2） 逆铣且0＜α≤θ，

（1） 顺铣时，0＜2π-α≤θ，V与Z+反向且ei为凹弧；

（2） 顺铣时，0＜2π-α≤θ，V与Z+同向且ei为凸弧；

（3） 逆铣时，0＜α≤θ，V与 Z+同向且 ei为凹弧；

（4） 逆铣时，0＜α≤θ，V与 Z+反向且 ei为凸弧；

则ei处存在拐角。另拐角半径R较大时，当前刀具在此处开展拐角加工也没有意义，因为此时拐角位置处的切削余量较均为，且切削量不大，并设此时最大半径为即当拐角半径满足时拐角加工。

上述线链 c(e1,e2,…,en)的构建与边 ei类型判定首先需要提取ei端点，在此基础上根据程序段的功能字类型确立ei类型。ei端点与每程序段内的坐标点一一对应。其计算方法如下：

点坐标计算方法

（1） 编程方式为G90，即绝对坐标编程，则直接提取该程序段x, y, z坐标，若当前程序段缺省x, y, z中某一个或两个，则该缺省坐标与前一程序段一致。

（2） 编程方式为G91，即相对坐标编程，则提取程序段x, y, z坐标，若前一程序段计算得到坐标为(x1, y1, z1)，则当前程序段的点坐标为(x1+x, y1+y, z1+z)。

圆心坐标与圆弧半径计算方法 圆弧起点与终点参照点坐标计算方法即可，圆心计算依赖于程序段表达方式。一般常用表达有：

（1） 增量式，以I, J, K表示圆心相对圆弧起点的增量，则圆心坐标可表示为(x1+I, y1+J, z1+K)，其中为起点坐标(x1, y1, z1)。此时与 G90和G91编程方式无关。

（2） 半径式，以半径R与起点pts及终点pte表示圆弧，圆心没有直接给出，且R>0，表示圆心角α＜180°，否则 R＜0。设圆弧起点 pts与终点pte连线中点为ptm，圆心为pto计算则按以下

步骤：

①向量可表示为，其中函数sgn(R)为半径R的取符合函数，

② 中点 ptm与圆心 pto距离

③ 圆心坐标pto为pto=ptm+l*vm。

（3） 圆心式，直接采用I, J, K表示圆心。依上述方法及原理，针对程序段与线链c(e1,e2,…,en)开展和拐角识别的准则如下：

准则3 若准备功能字为G01，则前一程序段坐标点 pt1至当前程序段坐标点 pt2为直线插补，即pt1为起点，pt1为终点，构成直线e。

准则4 若准备功能字为G02或G03，则前一程序段坐标点pt1至当前程序段坐标点pt2为圆弧插补，即pt1为起点，pt1为终点，构成圆弧e。

准则5 若当前程序段的点不在线链所构成的平面内，则当前线链识别终止。

准则6 若线链起点与终点重合，则该线链为封闭环，若线链c(e1,e2,…,en)中连续m条直线该m条直线的顶点序列为若均不存在拐角，则从自q=1至q=m-4每取4点构成一平面圆，若自q+4至第q+3+i点均在该圆上，则可构成一圆弧，按圆弧判定原理，确认是否为拐角。若是拐角，则说明该拐角为由离散点构成，也是拐角一种形式，称为离散式拐角。

1.3 拐角加工

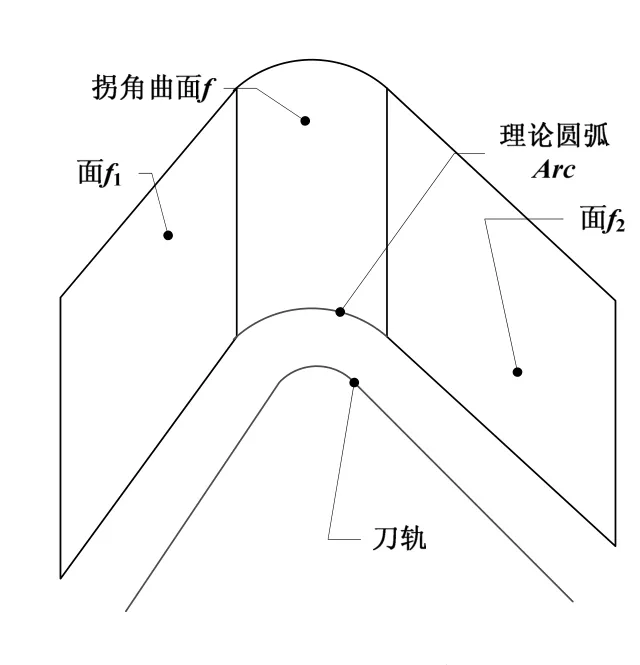
图1 拐角结构示意图

图2 拐角分层加工示意图

其中，H1称为进刀点，E1为切入点，F1为切出点，K1为退刀点。各点计算方法如下：

1） E1由拐角点沿-V，计算累计长度时得到；

2） F1由拐角点沿V，计算累计长度时得到；

3） 按方向 V计算 E1处切矢 v1，得矢量v3=V×v1，按H1=E1+ w1∗v3得到点H1坐标；

4） 按方向 V计算 F1处切矢 v2，得矢量v4=v2×V，按K1=F1+ w5∗v4得到点K1坐标。

按上述计算过程与图2中所示原理计算各层刀轨，每层刀轨的坐标点x与y值均相同，仅z坐标为各层刀轨所在高度，且为0＜i≤n，n为刀轨分层数其中[ ]为取整函数。

因此拐角加工可表述为：

1） 若在线链c(e1,e2,…,en)中存在某处拐角，分别计算进刀点H1、切入点E1、切出点F1与退刀点K1，以及各层刀轨的Z坐标；

2） 当刀具加工至E1时，按v3方向快速定位至H1；

3） 快速抬刀至H4（与H1的x, y一致），即顶面设置高度Z1处；

4） 然后进刀段、切入段、拐角加工段、切出段与退刀段顺序开展拐角铣削，至退刀点K4；

5） 按退刀连接线，刀具快速定位至第 n-1层刀轨的进刀点，如H3，重复步骤(4)；

6） 直至完成第i=1层加工，切出点至F1，然后按原始刀轨顺序加工，而不需要退刀至K1。

若相邻两拐角C1和C2加工程序，C1的切出段l4与C2的切入段l2存在重叠，则将C1和C2加工程序进行合并，省略C1的退刀段l5和C2的进刀段l1，直接将C1的切出段l4与C2的切入段l2相连。若线链为 c(e1,e2,…,en)为封闭，则由 e1之终点按V和起点按-V方向提取最近拐角C1和C2，并判定该两拐角加工程序是否重叠，如果重叠，则将两拐角加工程序合并。

2 算法实现与验证

2.1 算法实现

本研究识别NC代码中拐角并自动生成拐角加工程序。其输入、输出分别为：

输入 NC代码文件与辅助参数，其中辅助参数包括：需加工的拐角最大张角θ，进刀段l1、切入段l2、切出段l4及退刀段l5长度w1，w2，w4及w5，最大半径拐角加工分层高度h与顶面设定高度Z1。

输出 添加拐角加工后的NC代码文件。

依据输入NC文件与输出要求，则开展拐角识别并自动生成拐角加工程序算法流程如下所示。

Step 1 搜索NC文件，判定G91或G90，分析编程方式。

Step 2 按行读取程序段，按点坐标计算方法，计算各程序段绝对点坐标，并依据G01、G02、 G03关键字，构建直线与圆弧边，并按识别规则5，完成线链构建。

Step 4 由方向Vi计算ci之各边eij在端点处的切矢。

Step 5 对各线链ci按和拐角判定原理及规则6识别和拐角。

Step 6 按进刀点，切入点，切出点与退刀点计算方法，得到相应各点，计算分层数与各层Z坐标。

Step 7 判定线链是否封闭及各相邻拐角切入段与切出段是否重合，对重合拐角加工的切入段与切出段进行合并，得到组合拐角加工。

Step 8 提取切入段l2、转角加工l3、切出段l4加工NC程序段，修改相应Z坐标，得到各层切入段、转角加工、切出段加工NC程序段。

Step 9 分别在各层拐角加工的NC程序段前与后添加进刀段与退刀段及进退刀连接段代码，并写入原始文件。

Step 10 如此重复Step3 至Step9，完成各ci内拐角处加工程序，保存NC代码文件。

2.2 实例验证

为验证本文所提出方法的正确性，以一实例为证。实例原始加工导引线的拐角处基本尺寸如图3所示，该实例包含了和拐角及组合拐角。加工刀具直径φ20mm，采用西门子840D控制系统生成的NC代码，并设拐角最大识别角度θ=120°，最大半径为最大加工高度Z1=40mm，分层高度h=15mm，切入段与切出段距离w2=w4=15mm，进刀段与退刀段距离w1=w5=3mm，如图4所示。

图3 原始加工导引线与NC文件的加工刀轨

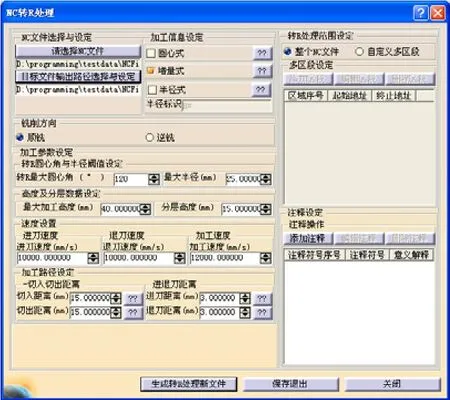
图4 拐角识别基本参数界面

通过读取NC文件，按照识别算法，并借助CATIA软件的二次开发显示添加拐角加工后的刀轨，如图5所示。图中识别拐角6个，拐角4个，有一原始半径为R=40拐角大于不做拐角处理，构建组合拐角3个。按照分层加工思路，该实例共分n=[40-0/15]+1=3层，每层刀轨按照进刀、切入、拐角加工、切出与退刀完成，层间刀轨通过进退刀连接线连接。

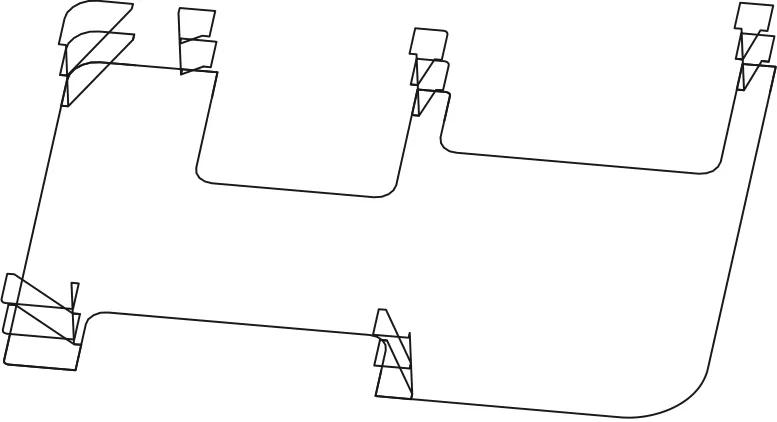
图5 拐角分层加工刀轨实例图

经该实例验证，本文提出的针对NC代码开展拐角识别与程序自动构建算法是正确的，并通过分层铣削，直接在刀具轴向上控制切削量，宏观上降低了刀具瞬间切削量，保证切削安全；并采用原始加工刀轨，保证了加工表面质量。同时本文提出的算法已经作为一项辅助工具内嵌于北京航空航天大学与沈阳飞机工业集团有限公司联合开发的“飞机复杂结构件快速数控编程系统”中，且该工具正在该公司推广应用，经应用反馈，该算法合理可行。

3 结 论

本文针对NC代码开展拐角识别并按照分层铣削原理构建了拐角加工程序，减少了刀具在拐角位置瞬时切削量。首先分析了NC代码中与拐角相关代码结构与功能字，将拐角类型分为点式拐角与圆弧式拐角两大类。其次将 NC代码还原刀轨的几何形态，采用线链表示，并计算线链走向及在走向下各端点切矢，通过切矢夹角大小、顺、逆铣削方式、圆弧的凹凸性等参数识别和拐角。然后按照进刀、切入、拐角加工、切出与退刀五段铣削方式完成分层拐角加工，层间刀轨由进退刀连接线衔接。最后，给出了验证实例，对本文所提方法进行计算和测试，验证了该方法的正确性和有效性。该算法目前已经在沈阳飞机工业集团有限公司开展应用，进一步验证了其可行性。目前该算法需要进一步推广应用，以确保适应各类型的数控加工系统的NC代码，确保其具有较高的覆盖率，进一步扩大工程应用；同时需要进一步探究带有样条插补的NC程序的拐角加工。

[1] 梁 全, 王永章, 富宏亚, 等. 直纹面叶轮插铣加工关键技术[J]. 计算机集成制造系统, 2010, (1): 182-187.

[2] 胡俊志, 黄 翔, 李迎光. 型腔转角插铣粗加工方法[J]. 机械制造与研究, 2008, 37(3): 37-39.

[3] Zhao Zhenyu, Wang Chengyong, Wu Shixiong, et al. Pocketing toolpath optimization for sharp corners [J]. Journal of Materials Processing Technology. 2007(192–193): 175-180.

[4] Choy H S, Chan K W. A corner-looping based tool path for pocket milling [J]. Computer-Aided Design. 2003, 35(2): 155-166.

[5] 吴 琼, 张以都, 张洪伟. 航空薄壁型腔件拐角铣削加工的研究(英文)[J]. Chinese Journal of Aeronautics, 2009, (6): 677-684.

[6] 程志刚. 高速铣削型腔拐角工艺研究[D]. 广东工业大学, 2006.

[7] 李开柱. 拐角高速铣削工艺试验及刀具轨迹优化研究[D]. 广东工业大学, 2012.

[8] 吴世雄, 李开柱, 汪 磊. 高速铣削拐角刀具轨迹优化[J]. 机械设计与制造, 2012, (8): 245-247.

[9] 赵 军, 张桂梅, 曲仕茹. 利用极点顺序的多边形顶点凹凸性判别算法[J]. 工程图学学报, 2007, 28(1): 55-59.

[10] 刘晓平, 吴 磊. 简单多边形方向及顶点凹凸性的快速判定[J]. 工程图学学报, 2005, 26(4): 124-129.

Automatic Generation of Corner Machining Program for Planar Profiles during Post-processing

Rao Youfu1, Zheng Guolei1, Chen Jun1, Du Baorui2, Chu Hongzhen2
( 1. School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China; 2. Shenyang aircraft industry group co., LTD, Shenyang Liaoning 110034, China )

To solve the problem of early NC programs lack of corner processing, an algorithm about corner recognition and automatical generation of processing program for planar profiles around NC code is proposed. This method can meet the product upgrades and high processing requirements of NC machining, and further ensure the security and the surface quality of parts. Firstly the common NC code structure is summed up. Secondly the NC Code geometry representation is expressed as edge chains. Then the direction of those chains and the edge tangent in chains are computed. And the corners are classed as point and arc corners. At the same time, the recognition rules of corner, considering these factors such as discrete structure of arc corner and closure of chains, are presented. To reduce the instantaneous cutting amount of processing at the corner position from the tool axis, Corner machining is layered. Each layer of corner processing tool path consists of feeding, cutting in, corner processing, cutting out and retracting sections. Layers of path are connected with feeding-retracting lines. Finally, an experimental result is showed to prove this algorithm.

numerical control processing; corner processing; NC code; post-processing

TP 391.7

A

2095-302X (2013)03-0058-07

2013-01-16；定稿日期：2013-02-27

国家高档数控机床与基础制造装备科技重大专项基金资助项目（2012ZX04010051）；沈阳市科技创新专项基金资助项目会（F10-003-2-00）

饶有福（1984-），男，江西鹰潭人，博士研究生，主要研究方向为CAD/CAM/智能工装设计技术。E-mail：beihanghu@163.com

郑国磊（1964-），男，福建莆田人，教授，博士生导师，主要研究方向为CAD/CAM，夹具智能化设计和数字化装配。E-mail：zhengguolei@buaa.edu.cn