道路因素对车辆侧翻的影响分析

孙 璐 游克思 王易阳 王登忠 顾文钧

(1 东南大学交通学院，南京210096)

(2Catholic 大学土木工程系，华盛顿20064)

(3 河海大学大禹学院，南京210098)

据美国公路交通安全管理局(NHTSA)统计，美国每年约有1.1×107起交通事故，其中车辆侧翻事故数虽然只占所有交通事故总数的2.5%，但由其引起的死亡人数占整个交通事故死亡人数的比例却很高［1］.车辆侧翻事故的严重程度明显高于其他类型交通事故，是导致人员伤亡的主要事故类型.

车辆侧翻通常与其质心高度、轮距、悬架和轮胎特性等车辆自身参数密切相关，文献［2-4］对这些影响因素进行了系统的研究.交通事故通常是由人-车-路多方面因素综合交互作用引发而成的.现有的事故统计资料表明，驾驶员操作行为、道路及路侧环境对车辆的侧翻也有一定的影响［5］.然而，哪些道路因素对车辆侧翻有影响以及各因素的影响程度如何则鲜有报道.

现有路线设计以传统静力学理论为基础，通常将车辆简化为刚体，忽略了车辆侧倾运动以及不同车型间结构的差异，且主要考虑车辆的侧滑［6］.已有研究表明，重心较高的车辆在干燥路面上行驶时，发生侧翻的可能性高于发生侧滑的可能性［7］，因此，在这种情况下设计出的道路虽然满足相应的规范标准要求，但对于道路上具有高重心的车型来说是不利的.故有必要进一步探索道路因素对车辆侧翻的影响以及这些影响因素的显著性，为今后的道路安全设计提供参考.

鉴于上述研究中存在的不足，本文构建了一种人-车-路闭环仿真模型，建立了侧翻的风险度量指标，并采用正交试验设计方法，系统地研究了平曲线半径、纵坡、超高、摩擦系数、缓和曲线设置等单项因素以及各因素间交互作用对车辆侧翻的影响.

1 人-车-路闭环仿真模型

1.1 道路模型

道路几何线形包括平曲线、超高、纵坡、合成纵坡等.道路平曲线通常由直线、缓和曲线以及圆曲线等连接而成.当道路曲线段和纵坡路段重叠时，出现了道路的合成纵坡，即路线纵坡与超高所组成的坡.图1中，R 为平曲线半径，is为超高坡度，isl为纵坡坡度，ic为合成纵坡度，且

由于道路设计超高，纵坡较小，故道路的横坡角度e 近似等于超高，即e ≈is;同理，纵坡角度θ近似等于纵坡坡度，即θ≈isl，合成纵坡角度θc≈ic.

1.2 车辆模型

1.2.1 整车模型

车辆三自由度模型是一种比较常见的模型，包括悬挂质量的侧向、横摆和侧倾运动.建立车辆模型时，首先假设汽车作稳态转向时，不考虑纵向运动以及空气作用力的影响.图2为三自由度整车模型示意图.图中，ms为悬挂质量;ay为侧向加速度;δ 为前轮转角;a，b 分别为质心距前、后轮的距离;cf，cr分别为前、后轮距;h 为重心高度;hc为质心距侧倾中心的距离;hf，hr分别为前、后侧倾中心距质心的距离;Fyf1，Fyfr，Fyr1，Fyrr分别为前左轮、前右轮、后左轮、后右轮侧向力;Fzf1，Fzfr分别为前左轮、前右轮垂直力.

图1 道路几何参数

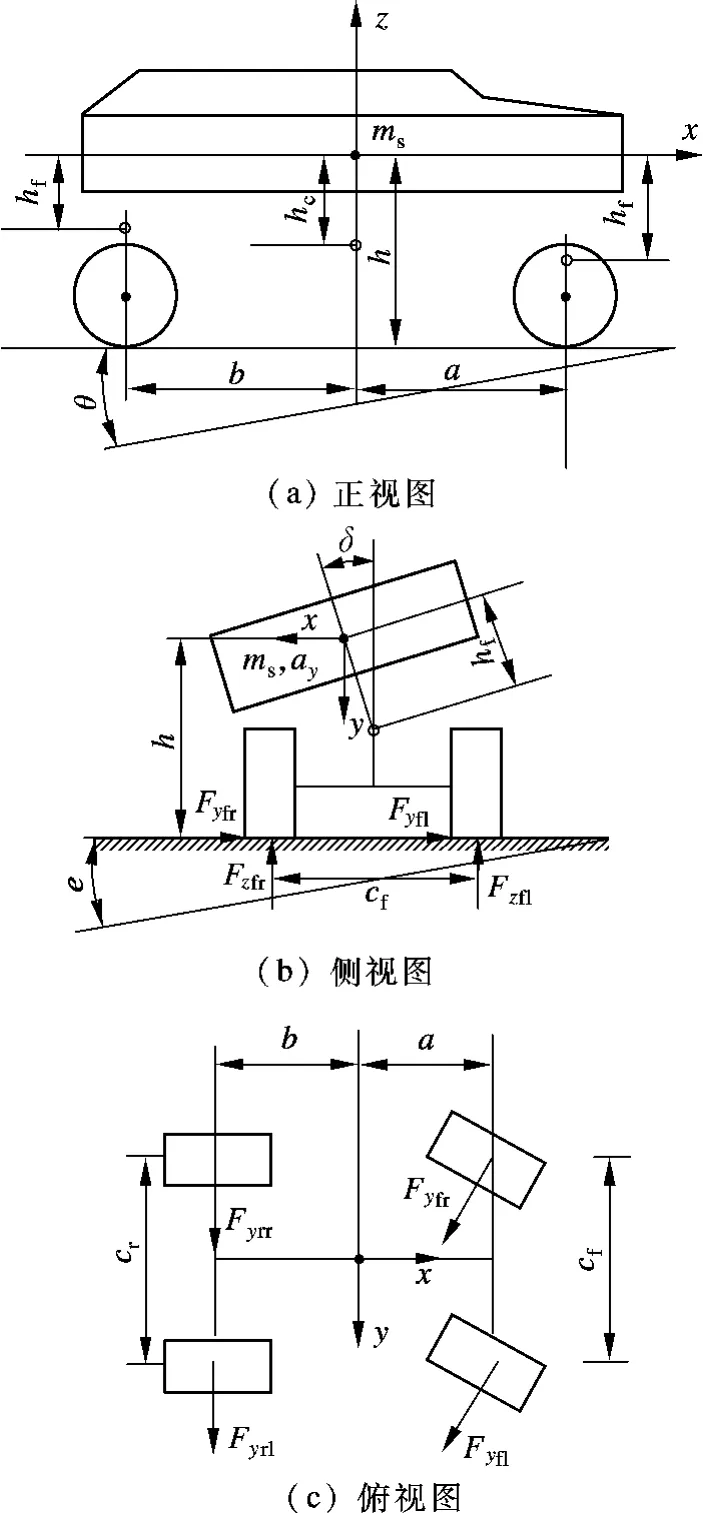
图2 三自由度整车模型

根据牛顿运动定律，可得到运动微分方程组.当车辆沿y 轴方向侧向力平衡时，有

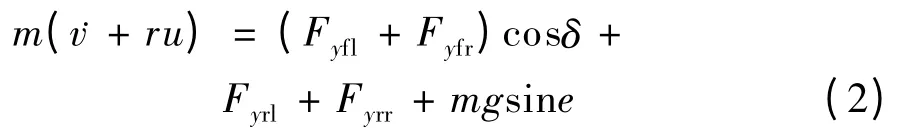
当车辆绕质心横摆力矩平衡时，有

当车辆绕侧倾中心侧倾力矩平衡时，有

式中，m 为车辆质量;r 为横摆角速度;v 为车辆纵向速度;u 为车辆侧向速度;Ix，Iz分别为悬挂质量绕x 轴和z 轴的转动惯量;Mz为悬挂质量绕z 轴的力矩;Kφf和Kφr分别为前、后悬架侧倾角刚度;bφf和bφr分别为前、后悬架阻尼系数;p 为侧倾角速度;φ 为侧倾角.

1.2.2 轮胎模型

轮胎垂直力与车辆的运动状况以及道路环境有关.当车辆匀速直线行驶时，左、右轮胎垂直力基本相同;但在弯道、斜坡上行驶或在加速、制动时，车辆前、后轮以及左、右轮均发生荷载转移，致使轮胎的侧偏特性和车辆的稳态响应发生变化.一般而言，轮胎的垂直力可以表示为

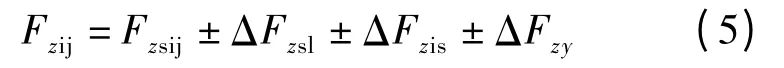
式中，Fzsij为车辆静止在水平路面上时车轮的垂直力;ΔFzsl为道路纵坡引起的荷载转移;ΔFzis为道路超高引起的荷载转移;ΔFzy为车辆侧向运动引起的横向荷载转移.由于本文不考虑车辆的加、减速情况，因此忽略由加减速引起的纵向荷载转移.

根据车辆在具有纵坡道路上行驶时的受力情况，忽略车辆滚动阻力和空气阻力，分别以轮胎前、后轮接触点为原点，根据力矩平衡可得

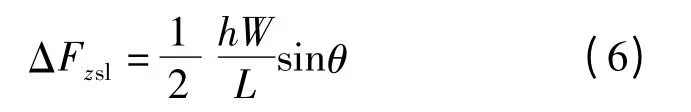
式中，W 为车辆所受的重力;L 为轴距.当θ 为正时为上坡，反之为下坡.

同理可得

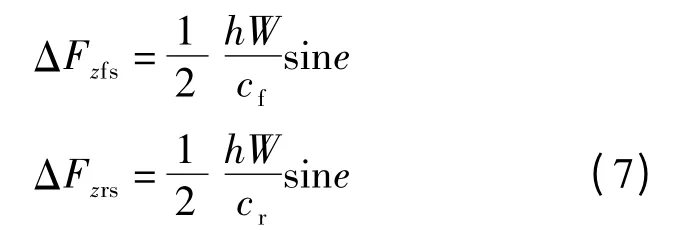
式中，ΔFzfs，ΔFzrs分别为前、后部内侧轮向外侧轮的垂直力转移量.

车辆在弯道上行驶时，受到侧向力和车身的侧倾作用，内侧轮胎荷载向外侧轮胎转移，荷载转移量与车辆侧倾角、侧倾角速度、侧向加速度等有关.根据文献［8］可得前、后部内侧轮和外侧轮的荷载转移量分别为

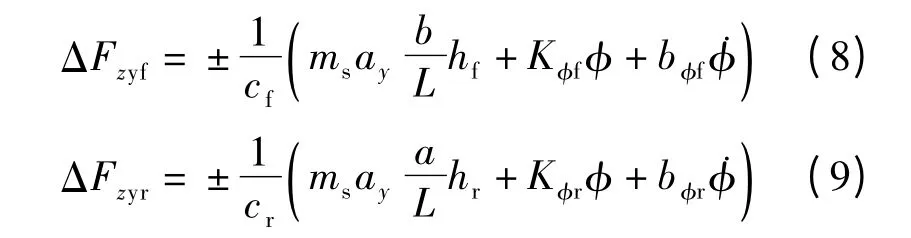
将式(6)～(9)代入式(5)，即可得到各车轮的垂直力.

应用“魔术公式”模型计算轮胎侧向力［9］.为分析不同路面摩擦系数下轮胎力情况，本文采用线性相似分析方法，假设在不同路面摩擦系数下，轮胎侧偏之间呈线性关系，得到任意摩擦系数u 的侧向力Fyu与摩擦系数u0的侧向力Fyu0的关系为

式中，Fz为轮胎垂直力;λ 为车轮侧偏角.

1.3 驾驶员模型

采用单点预瞄最优加速度模型［10］，即当道路方向角变化较大时，根据车辆的方位角ψ，可将道路函数从绝对坐标中转换到相对坐标后作为系统输入.设车辆重心的绝对坐标为(X，Y)，相对坐标为(x，y)，道路函数在绝对坐标下可表示为Y =Y(X)，在相对坐标下可表示为y =f(x).在预瞄时间为T 的情况下，预瞄点P 在相对坐标下的横坐标为

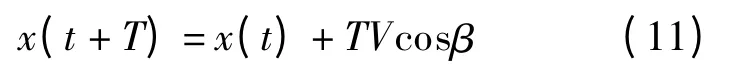
式中，β 为行车方向与相对坐标轴之间的夹角.预瞄点P 在相对坐标系下的纵坐标为

求解时采用理想状况，车辆模型采用1.2 节中建立的三自由度整车模型.车辆可以设置为匀速运动，也可设定为速度沿路线方向变化.采用Matlab软件中的Simulink 仿真模块建立仿真模型.

2 车辆侧翻风险的仿真分析

2.1 车辆侧翻及风险度量指标

车辆在弯道上行驶时，速度越大，受到的侧向加速度越大，车辆内侧的垂直荷载则越小，即内侧荷载向外侧转移.当内侧荷载垂直力减小到0 时，车辆在侧倾平面内将不能保持平衡，开始绕外侧轮胎接触点形成的轴线翻转，这时车辆非常不稳定，极易发生侧翻事故.本文选取侧向加速度ay和荷载转移比LTR 作为度量车辆侧翻风险的指标.其中，LTR 定义为内侧车轮转移到外侧车轮的荷载与总荷载之比［11］，即

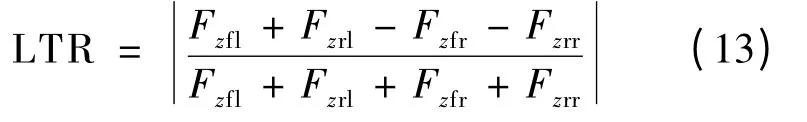
式中，Fzrl，Fzrr分别为后左轮、后右轮垂直力.

本文选用安全裕度来反应评价指标接近侧翻阈值的程度.第j 个动力学指标Ij(t)随时间变化的曲线见图3.由图可知，Ij(t)越接近阈值I0j 时，车辆发生侧翻的可能性越大.

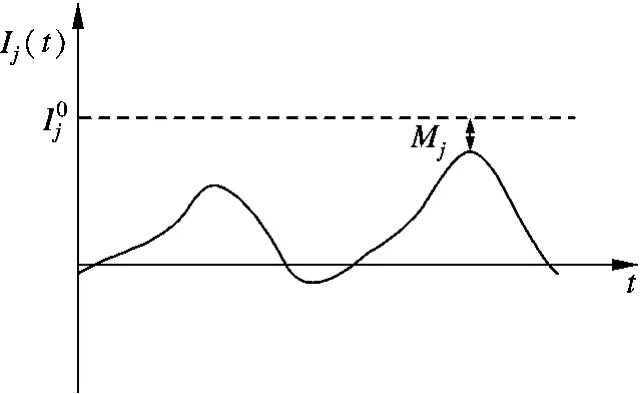
图3 第j 个动力学指标随时间变化曲线

因此，侧向加速度ay(j = 1)和荷载转移比LTR(j =2)对应的2 个安全裕度分别为

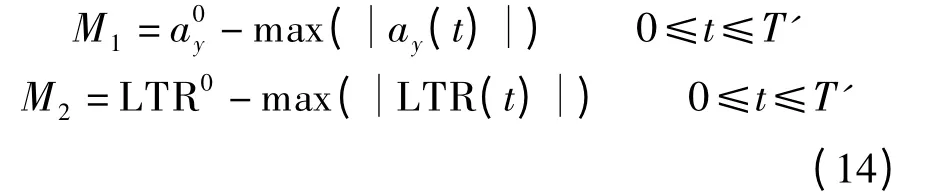
式中，T′为仿真时间;a0y 为临界侧向加速度;LTR0为临界荷载转移比.当内侧车轮荷载为0 时，内侧车辆离地，此时荷载转移比的阈值为1.

本文选择具有较高重心高度的运动型多用途(SUV)为模拟车型，车辆参数见表1.采用车辆“J型”转弯仿真模拟试验，不断改变车辆速度，直至荷载转移比为1，将此时对应的侧向加速度定义为该车侧翻的临界侧向加速度，通过模拟得到该车型的临界侧向加速度a0y=0.748g.

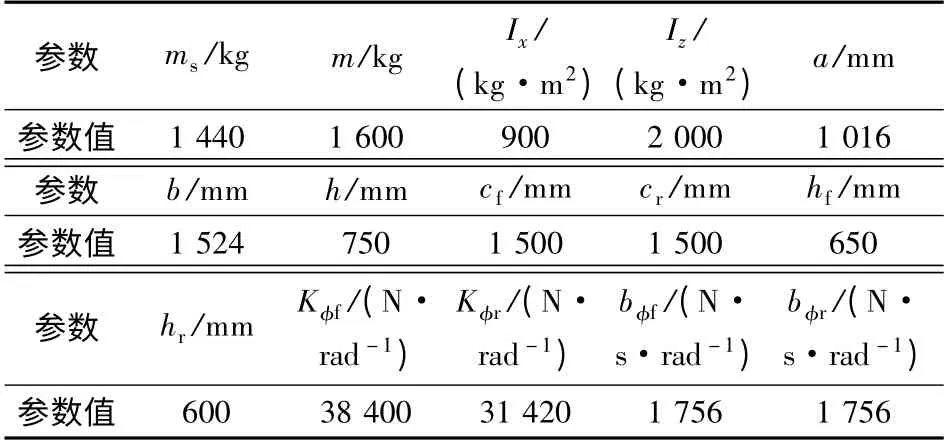
表1 整车参数

2.2 存在交互作用的混合水平正交试验设计

本文采用正交试验设计方法分析平曲线半径(A)、纵坡坡度(B)、超高(C)、路面摩擦系数(D)以及缓和曲线设置(E)等5 种道路因素对车辆侧翻的影响.各因素对应的水平见表2.

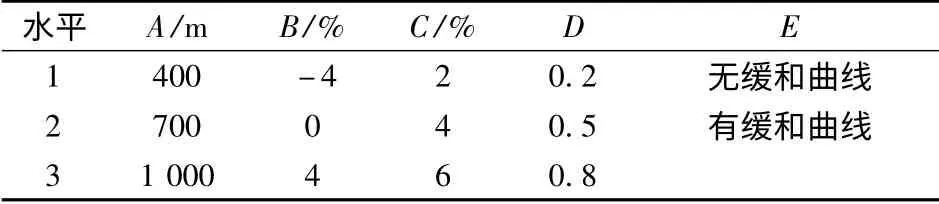
表2 因素及水平表

由表2可知，因素A，B，C，D 各包含3 个水平，而因素E 只包含2 个水平，各因素之间水平数不同.采用拟水平法，将因素E 的第2 水平重复一次，作为第3 水平，从而转化成等水平数问题的正交设计.同时，本文还考虑了因素间交互作用对车辆侧翻的影响.交互因素包括:①平曲线半径和纵坡坡度;②平曲线半径和超高;③平曲线半径和路面摩擦系数.每个因素包含3 个水平，因此可以套用等水平正交表L27(313).正交试验的表头设计中，列号1～列号11 分别表示因素为A，B，(AB)1，(AB)2，C，(AC)1，(AC)2，D，(AD)1，(AD)2，E;列号12 和列号13 为空白列，作为误差项.

2.3 试验结果与分析

分别计算基于临界侧向加速度和横向荷载转移比2 个度量侧翻风险的指标M1和M2.在此基础上进行方差分析，采用F 检验法进行因素显著性检验.对于给定的显著性水平α，从F 分布表中查出Fα.若第i 因素的F 值Fi≥Fα，说明第i 因素的变化影响大于误差的影响，即该因素影响显著［12］.对于不同显著性水平α，检验标准当Fi≥F0.01时，高度显著;当F0.01＞Fi≥F0.05时，影响显著;当F0.05＞Fi≥F0.1时，一般显著;当Fi＞F0.1时，不显著.

由表3可知，采用基于侧向加速度的安全裕度指标M1度量车辆侧翻风险时，FA＞F0.01(2，4)，FC＞F0.01(2，4)，FAC＞F0.01(4，4)，说明平曲线半径、超高及两者间交互作用对车辆侧翻具有高度显著性的影响.在给定的车辆运行速度下，平曲线半径直接影响车辆的侧向加速度大小以及车辆的侧倾作用，道路超高的设置在一定程度上抵消了车辆在曲线上行驶时产生的部分离心力，同时也减少了车辆的侧倾程度，因而这2 个因素及其交互作用对车辆侧翻具有高度显著的影响.F0.05(2，4)＞FE＞F0.1(2，4)说明缓和曲线设置与否对车辆的侧翻也有一定影响，通过设置缓和曲线可使曲率渐变过渡，车辆的离心加速度也渐变过渡，从而不至于产生很大的侧向冲击.相比道路曲线半径、超高等因素，道路纵坡、路面摩擦系数等其他因素对车辆的侧翻影响较小.

采用基于荷载转移比的安全裕度指标M2度量车辆侧翻风险的方差分析结果见表4.表3与表4仅存在个别差异，如表4中因素E 对车辆侧翻的影响程度更强，说明衡量车辆侧翻风险的指标选择 不同会导致结论存在差异.

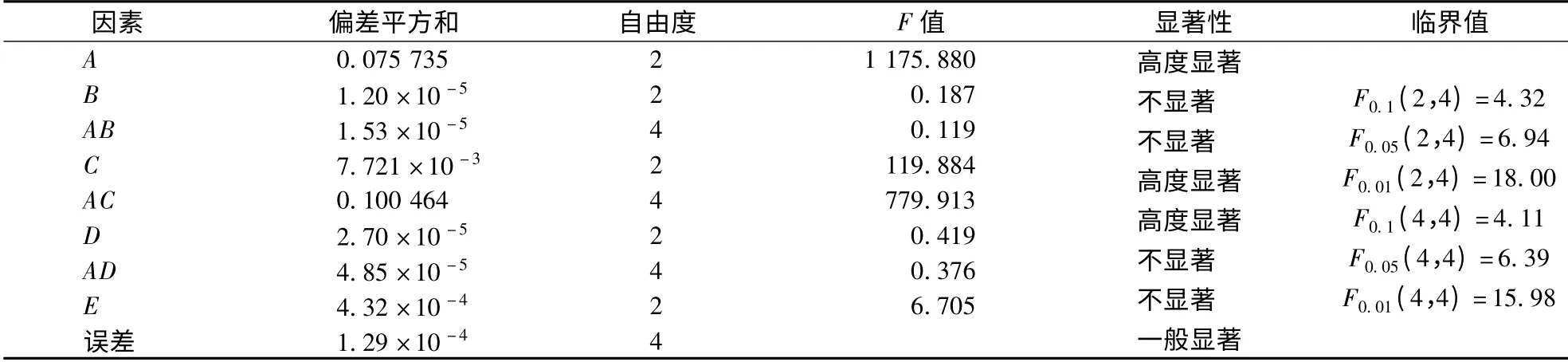
表3 基于侧向加速度的方差分析结果

表4 基于荷载转移比的方差分析结果

3 结语

本文利用Matlab 软件中的仿真模块Simulink构建了一种人-车-路闭环车辆动力学仿真模型，提出了2 个用于度量车辆侧翻的指标——临界侧向加速度和荷载转移比.在此基础上，采用正交试验设计，分析了不同道路因素以及因素间交互作用对车辆侧翻的影响.这些影响因素按照影响的强弱程度依次排序为:平曲线半径、平曲线半径与超高的交互作用、超高、缓和曲线设置、路面摩擦系数、平曲线半径与路面摩擦系数的交互作用、纵坡、平曲线半径与纵坡的交互作用，其中平曲线半径、超高、缓和曲线设置以及平曲线半径与超高的交互作用对车辆侧翻具有显著性影响.分析结果对今后的道路安全设计具有很好的参考价值.然而，影响因素的敏感性分析受度量车辆侧翻风险指标的影响，本文所选取的2 个指标能否真实反映车辆的侧翻风险还需在下一步工作中进行证实.

References)

［1］National Highway Traffic Safety Administration.An analysis of motor vehicle rollover crashes and injury outcomes［R］.Washington DC:NHTSA，2007.

［2］Randy W，William T，David M B，et al.A study of the effect of various vehicle properties on rollover propensity［C］//SAE World Congress.Detroit，MI，USA，2004:1-11.

［3］何锋，杨宁，郑秉康.影响载重汽车倾翻的主要汽车因素分析［J］.贵州工业大学学报:自然科学版，2011，30(4):92-95.

He Feng，Yang Ning，Zhen Bingkang.Analysis of main vehicle factors affecting heavy vehicle rollover［J］.Journal of Guizhou University of Technology:Natural Science Edition，2011，30(4):92-95.(in Chinese)

［4］沈明，王赟松，李志刚.基于仿真分析的汽车侧翻风险研究［J］.汽车工程，2009，31(12):1173-1176.

Shen Ming，Wang Yunsong，Li Zhigang.A research on the rollover risk of motor vehicles based on simulation analysis［J］.Automotive Engineering，2009，31(12):1173-1176.(in Chinese)

［5］Liu C.Factors related to fatal single-vehicle run-offroad crashes［R］.Washington DC:National Highway Traffic Safety Administration，2009.

［6］Easa S M，Dabbour E.Design radius requirements for horizontal curves on three-dimensional alignments［J］.Canadian Journal of Civil Engineering，2003，30(6):1022-1033.

［7］Transportation Research Board.Review of truck characteristics as factors in roadway design［R］.Washington DC:TRB，2003.

［8］余志生.汽车理论［M］.北京:机械工业出版社，2009.

［9］苏周成.车辆转弯制动稳定性动力学控制研究［D］.重庆:重庆大学机械工程学院，2007.

［10］郭孔辉.汽车操纵动力学［M］.长春:吉林科学技术出版社，1991.

［11］Kim Y，Kim G，Lim J.Sensitivity analysis of commercial vehicle parameters on dynamic rollover［C］//Proceedings of 13th IPC on Automotive Engineering.Gyeongju，South Korea，2005:51-62.

［12］邱轶兵.试验设计与数据处理［M］.合肥:中国科学技术大学出版社，2008.