氟化梯度折射率塑料光纤带宽特性计算

苗 圃 吴乐南

(东南大学信息科学与工程学院，南京210096)

塑料光纤(POF)由于其数值孔径大、纤芯粗、柔韧性好、价格低廉、易于与光器件链接等优点而越来越多地用于高速宽带接入网中.研究和测试表明［1－3］，氟化聚合物梯度折射率塑料光纤(PF－GIPOF)在近红外区域具有较小的衰减和微弱的模式色散且能够使用石英玻璃光纤(GOF)系统常用的光电器件而成为接入网中最优的传输介质选择.影响带宽的主要因素是色散［2－4］，因此建立准确的色散模型，选择最优参量，可有效地提高光纤的带宽性能和传输能力.

国内外众多学者对光纤的色散模型进行了研究.Kurt 等［5－6］考虑了部分参数作用下的传输特性而忽略了其他参数对系统性能的影响，该类模型具有一定的应用局限.Garito 等［7］考虑到了模式耦合但忽略了模式损耗因素，仅在光源满注入(OFL)条件下成立，给带宽的预测带来了限制.Gasulla等［8］推导出的多模光纤色散模型能够很好地描述其传输特性，但实现困难，形式复杂，适用于理论研究却不利于仿真计算.Yabre［9］分析了模式时延、耦合因子和衰减系数等因素，在限模注入(RML)和OFL 条件下推导出多模光纤色散模型，随后Ge等［10］在此基础上使用模式选择激励法提高传输带宽，但实验中细分的模式激励却不易准确实现.本文在文献［8－14］色散计算和模式耦合及损耗定量估计的基础上，综合考虑了折射率指数、材料色散、衰减系数、光注入条件和光源特性等因素，分析了全色散模型，借助数值计算研究了带宽特性，旨在选择最优的光纤参量进而提升传输带宽.

1 基带功率传输函数分析与推导

假设a 为纤芯半径，n1(λ)和n2(λ)分别为光纤轴心和包层处的折射率，λ 为激励光源的自由空间波长，α 为纤芯折射率分布指数，r 为距光纤轴心的距离，则PF－GIPOF 的折射率满足平方律分布:

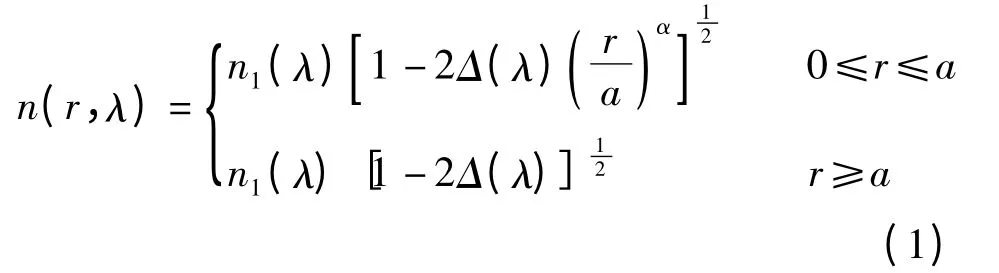
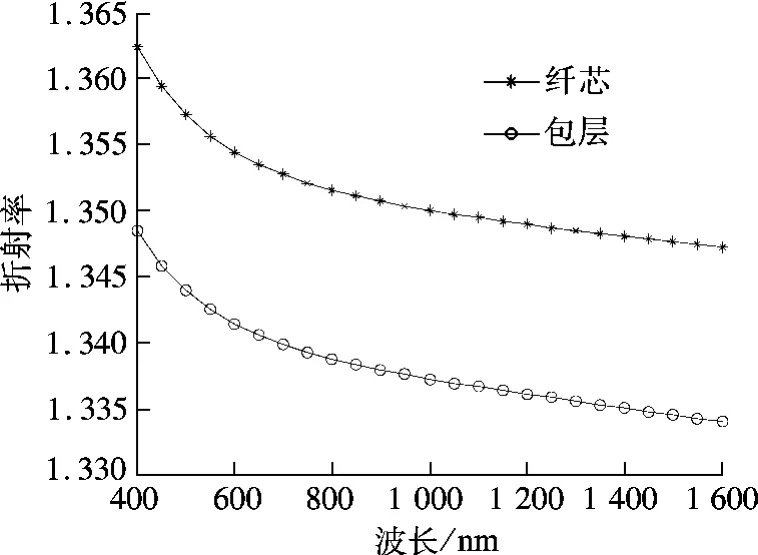
图1 PF-GIPOF 的折射率分布与工作波长关系

光纤中存在许多满足Maxwell 方程解的模式，每个传导模式的传输速度和传播常数各有差异，但近邻传导模之间的传播常数和速度却近似相等，可将这些近邻传导模组合为模群.通过WKB 法可计算出单位纤长的模群延迟为［9］

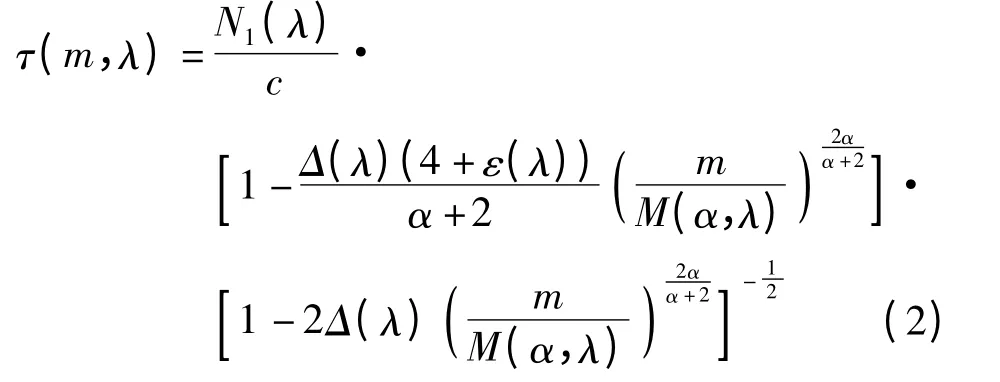
令光纤长度为z，Ω 为基带角频率，P(λ，λ0)为时间非相干光源的光谱分布，Ceff(m，λ)和L(m，λ，z)分别为光源对m 模群的激励系数和传输损耗，G(m，λ，z，Ω)为不同光入射条件下的模式耦合效应.假设式(1)所定义的PF－GIPOF 是线性系统，当a 较大且激励光源频谱线宽均方根W 满足［10］

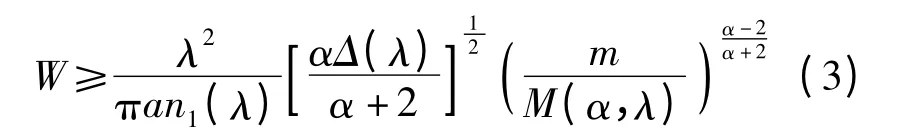
时，所激励出的模式之间排列就会异常紧密，可认为m 是连续值，那么m 和λ 对功率贡献的和值计算便可使用积分来代替.则在复频域内其基带功率传输函数可写为

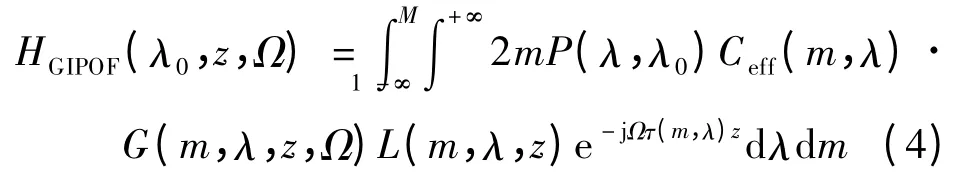
假设光源能量主要集中在中心波长λ0处，则Ceff(m，λ)，L(m，λ，z)和G(m，λ，z，Ω)可由它们在λ0处的值来代替，以简化模型的分析计算.

用泰勒级数对式(2)左半部分展开，可得

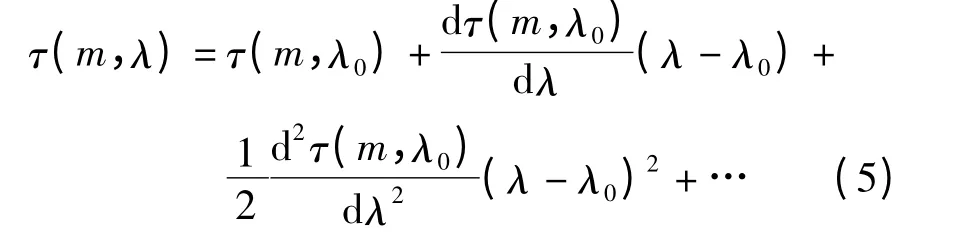
为简化计算，式(5)中第2 项和第3 项系数可分别由它们的平均值D0(λ0)和S0(λ0)来代替，取前3 项代入式(4)中，拆分化简后可得

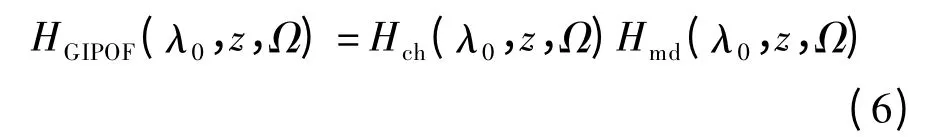
其中，色度色散效应传输函数为

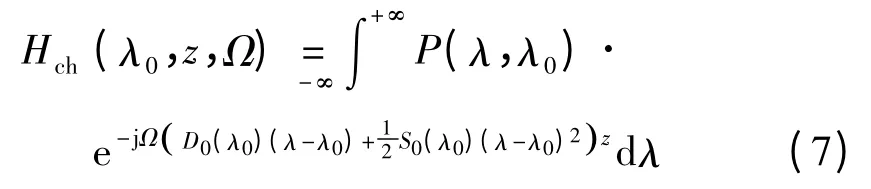
模式色散效应传输函数为

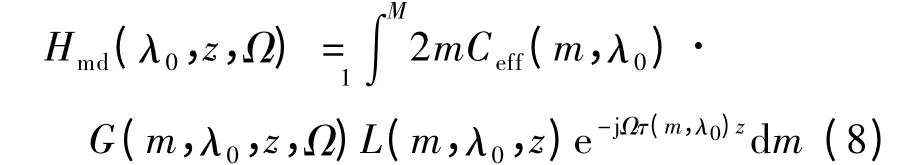
由式(6)～(8)可看出，PF－GIPOF 的基带功率传输函数可由2 个独立的函数乘积组成，且色度色散与时延相关，而光源激励、模式时延、差分模式损耗和模式耦合却决定了模式色散.

2 色度色散效应计算

假设光源功率谱具有高斯线谱分布特征，即

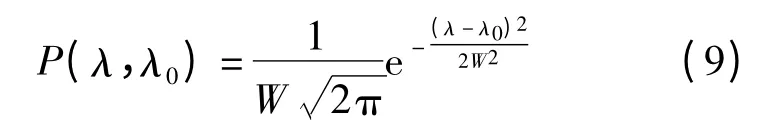
将式(1)、(2)和(9)代入式(7)中，计算得

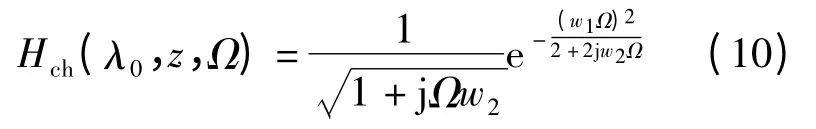
其中，w1=－ D0(λ0)Wz，w2=(S0(λ0)+2D0(λ0)/λ0)W2z.可看出，即使系统工作在零色散波长附近，由于S0(λ0)的存在，色度色散对带宽的影响也不能忽略.当远离零色散波长区域时对色度色散的制约作用可忽略.

3 模式色散效应计算

将式(8)对直流分量Hmd(λ0，z，0)进行归一化:

式中，R(m，λ0，z，Ω)=Ceff(m，λ0)G(m，λ0，z，Ω)·L(m，λ0，z)e－jΩτ(m，λ0)z为m 模群在复频域内的能量分布.

3.1 差分模式损耗的拟合

差分模式损耗(DMA)是指传导模由于路径不同造成各模式间损耗系数不同的现象.由于PFGIPOF 的制造材料、设备工艺及应用场合不同，因此DMA 至今没有统一确定的计算公式.模式损耗L(m，λ0，z)=e－αT(m，λ0)z，大量的实验数据拟合结果表明αT(m，λ0)满足修正的贝塞尔函数［9］，可表示为

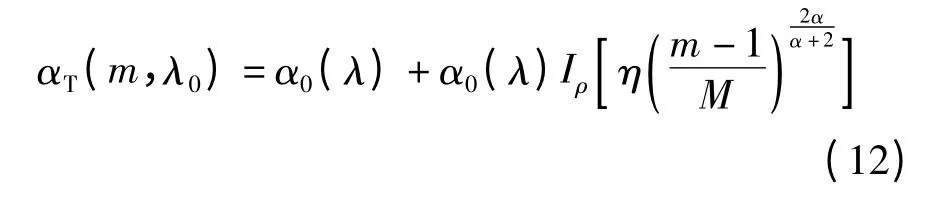
式中，α0(λ)为本征损耗;Iρ为ρ 阶修正的第一类贝塞尔函数;η 为权重因子.根据测试数据找出合适的拟合因子ρ 和η，便可得出L(m，λ0，z)的解析表达式.

3.2 模式激励系数

Ceff表示光耦合进入纤芯后不同传导模的功率比例，其值与光入射条件有关.在OFL 条件下，光斑直径与纤芯直径相当，光锥角大于光纤的数值孔径，传导模被均匀地激励，光波能量均匀分配，此时Ceff=1.而在目前中短距离高速数据传输试验中，所用光源大多选择受激辐射发光的半导体激光器或垂直腔面发射激光器，其发散角小、光束细且功率谱密度具有高斯线谱分布特征，注入到光纤截面的激光束直径小于纤芯直径，那么此时仅有部分传导模被激励承载光波能量，且各模式能量大小根据激光束半径、注入到纤芯截面处的坐标和入射角数值孔径的不同而各有差异.在RML 条件下，Ceff便可由激励模式和入射激光电场强度的交迭积分计算得到.

假设激光束中心和光纤截面轴心对齐，与其几何形状耦合匹配，在光纤截面则呈现出半径为w圆对称的近场光分布.设(x，y)为纤芯截面平面坐标，则该点处的电场强度为

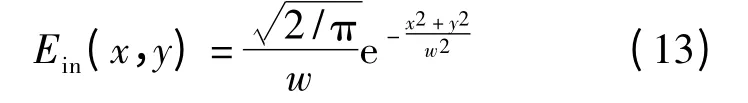
令Hu为u 次厄米特多项式，受激模式的厄米特－高斯场可近似表示为［10］

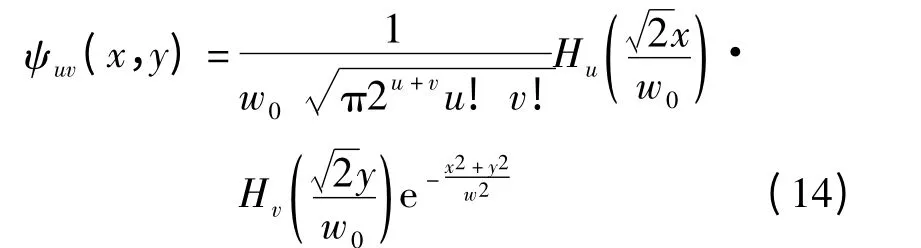
式中，w0为归一化激光束半径.则Ein(x，y)和ψuv(x，y)对纤芯截面的积分为

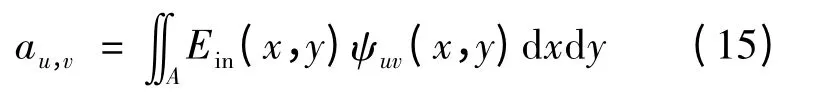
那么m 模群的功率激励系数均值为

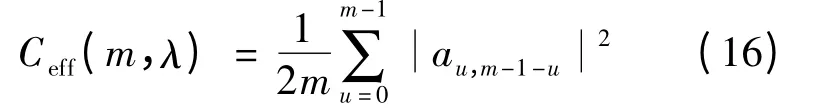
可求得被激励的模群数为

MGB(λ)=M(α，λ)·

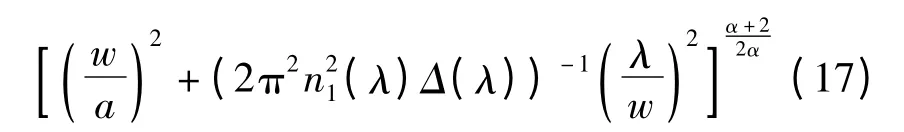
在一定的波长下，激光束所激励的初始模群个数与w 有关，受激模群越少，其能量差异就越小，各模群所承载的光功率越易趋于平衡，模群到达接收端的时间就越趋于一致，导致输出信号的脉冲展宽量就变小.因此，合理选择激光束半径，可以有效减小模式色散，提高传输带宽.

3.3 模式耦合函数

传导模沿光纤传播时，各模式之间非独立，能量会随机地在相邻模式间转移，引起能量重新分配.通过以上分析，Ceff，L 和τ 都可得到完整的解析表达，但由于模式之间能量转换的复杂性，却很难得出G 的解析表达.在基于传导模式为连续变量且能量耦合只发生在相邻模式间的假设条件下［11］，可通过能流方程来测量模式耦合系数.基于此，同样地可通过求解传导模的功率流方程来表示R(m，λ0，z，Ω).综合考虑式(11)中各个函数，参照Gloge 能流方程，可推出传导模的功率流方程为

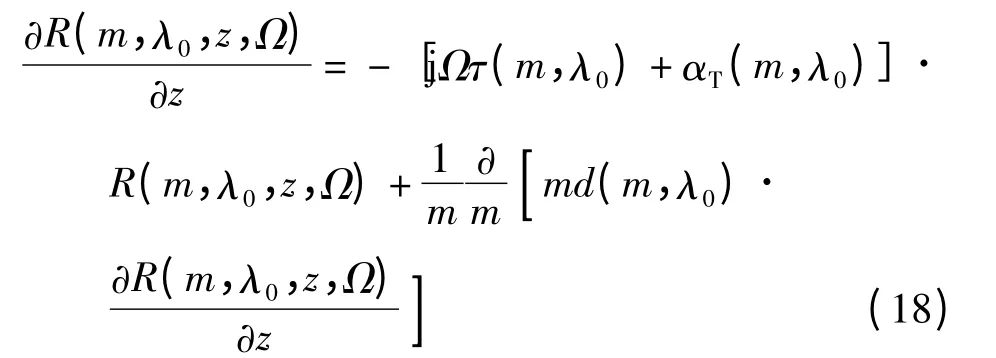
式中，d(m，λ0)为归一化到M2(λ0)的模式耦合系数.对于此类偏微分方程，使用Crank－Nicholson 的格式有限差分法便可以求出R(m，λ0，z，Ω)的数值解，相应地Hmd(λ0，z，Ω)也可计算求解.

4 计算结果与分析

通过以上分析可知，PF－GIPOF 的长度、折射率指数、工作波长、激励光源等参量影响着色度色散和模式色散，在不同条件下通过式(7)、(8)计算其频率响应进而可得到其带宽特性.由于模式耦合对带宽影响甚微，在以下计算中取G =1.

4.1 传输参量计算与仿真

假设参数z =200 m，α =2，λ0=1 300 nm，芯/包直径为120/490 μm，使用W =5 nm，w =20 μm的光谱高斯分布光源，通过式(1)可得n1=1.348，n2=1.336，Δ=0.009 5，数值孔径NA=0.186 1.在1 300，850 和650 nm 工作波长下，保持其他参量不变，计算单位长度模群时延，结果如图2所示.由图可见，650 nm 的高阶模群时延量要小于低阶模群，而1 300 nm 的情况与其相反，850 nm 的模群间时延的差异最小.

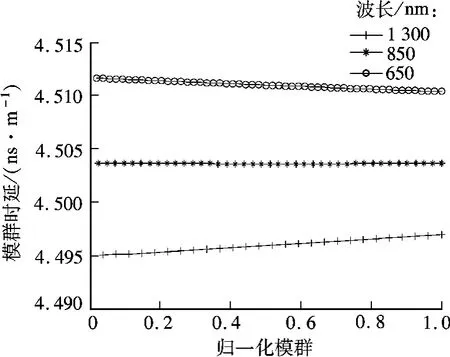
图2 不同工作波长下单位长度的模群时延对比

改变w，可得到被激励的模群数与w 在不同工作波长下的仿真对比，如图3所示.该类曲线呈开口向上的抛物线状，不同波长的光源所激励的模群总数也有所不同，可求得在w =11.76 μm 处的激励模群最少.因此合理选择w，使激励模群总量越少，其能量分配就越易趋向平衡状态，模群传播常量差异就愈小，色散效应也就越弱，进而传输带宽可得到相应提高.

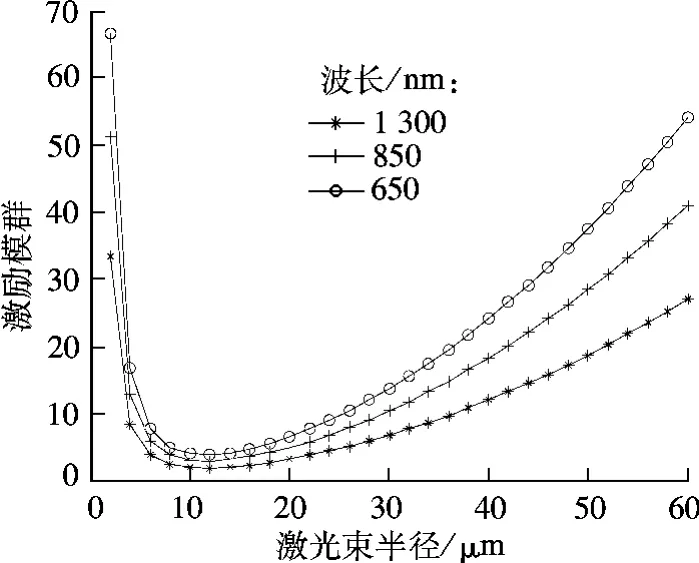
图3 不同光源激励的模群数目对比

4.2 不同条件下的频率响应计算与分析

令w =11.76 μm，z =100 m，采用文献［11－13］中的实验方法，取ρ =11，η =12.2 对式(12)数值拟合［14］，保持光纤其他参量不变，在考虑DMA 和忽略DMA 情况下，系统频率响应计算对比如图4所示.可以看出由于DMA 的作用，－3 dB 带宽从1.56 GHz 提升到5.12 GHz.由于高阶模群衰减大于低阶模群，在传输一定距离后，高阶模群会因剧烈衰减而消失，在输出端的最大相对延迟不再位于m/M =0 和m/M =1 之间，而是在m/M =0 和某个小于1 的模群之间.因此，高阶模的消失在一定程度上减小了模式间的最大时延，导致脉冲展宽减小，模间色散减弱.这从另一方面说明了DMA 对传导模具有“滤波”作用，其带宽的提高是色散和损耗的折中结果.取不同纤长的频率响应，在忽略DMA、考虑DMA、使用Gasulla［8］模型和Tolga［5］模型情况下，计算出的－3 dB 带宽分别为B1，B2，B3和B4，结果如图5所示.可看出，B2和B3接近，但B3形式复杂不利于仿真计算，B4从脉冲时延角度统计带宽，参数考虑不全面，结果与B1近似.

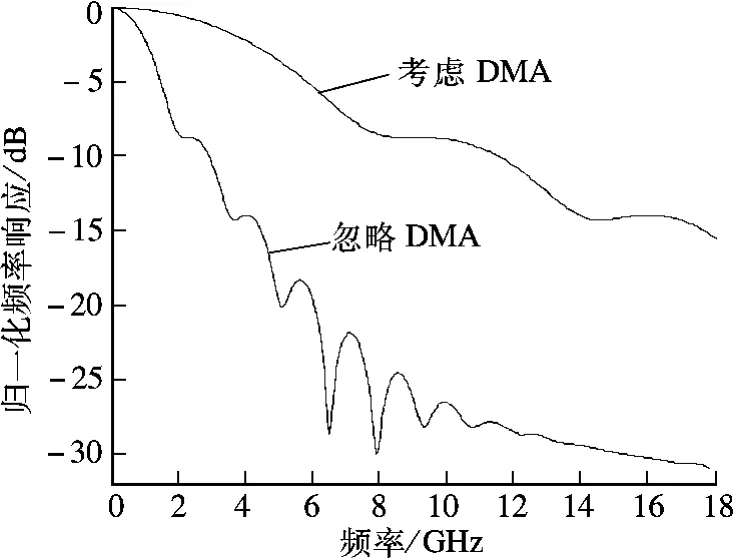
图4 考虑DMA 和忽略DMA 情况下的频率响应对比

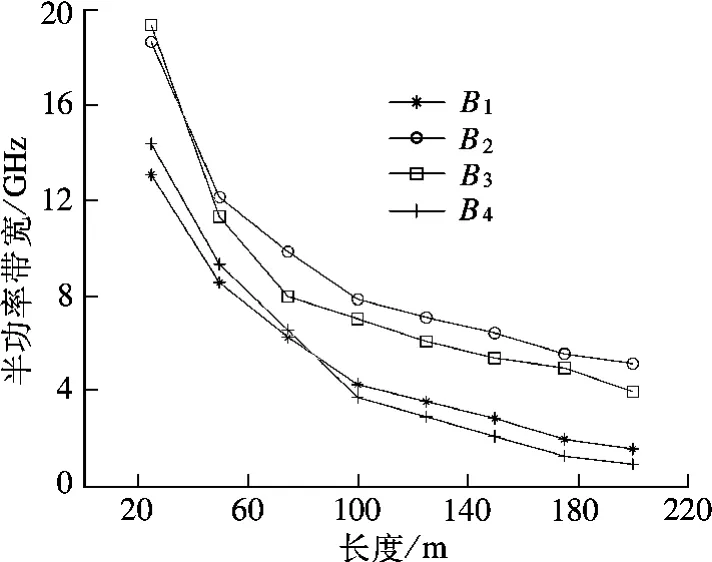
图5 －3 dB 带宽与光纤长度的关系对比

DMA 可提高传输带宽，但为了研究其他参数对带宽的影响，就必须忽略DMA 以免与其他参数的作用发生混淆.由于α 影响着纤芯折射率的分布情况，α 不同，传导模的路径也就不同.保持材料参数和光源参数不变，α 分别取1.8，2.0，2.1，2.16和2.3，得到的频率响应对比如图6所示.α 增大，带宽相应提高，但α 同时又影响着材料色散和模式耦合，并非愈大愈好.当α 逐渐增大以致折射率分布结构愈趋近于SIPOF 时，模式传播路径被延长，模式耦合便对传输特性起主导作用，带宽反而急剧下降.因此选择合理的α 可使模式间路程差最小，耦合效应最低，带宽最大.计算后可知，α =2.16 时对应的最优－3 dB 带宽为3.92 GHz.

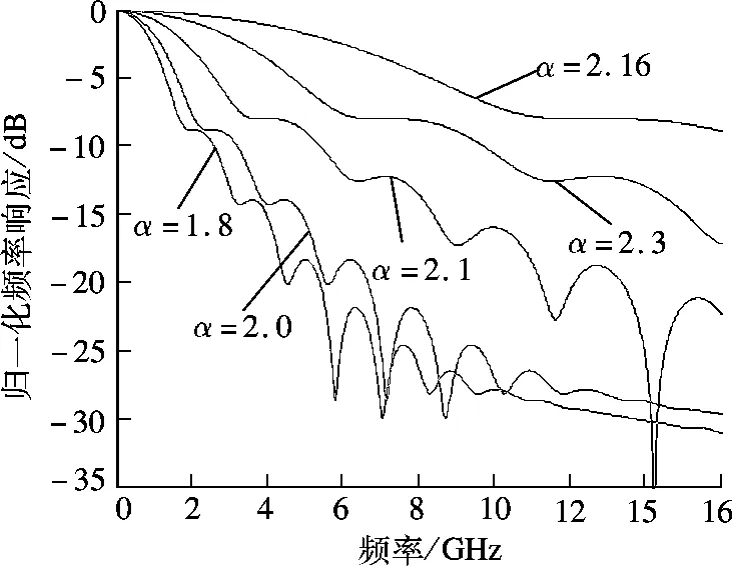
图6 不同折射率指数下的频率响应对比

同样地，α 仍取2.0，忽略DMA，其他参数同上，λ 分别取650，1 300 和1 550 nm 时，频率响应对比如图7所示.经计算可知尽管在1 550 nm 处存在较小的材料色散，但由于DMA 效应要比1 300 nm 处的小，在材料色散和DMA 对带宽的影响中，DMA 仍占据主导作用，因此－3 dB 带宽就小于1 300 nm 处的带宽.所以，波长对带宽的影响其本质是不同激励条件下的材料色散和DMA 共同竞争的结果.通过图4～图7的频率响应对比可知，带宽特性是众多传输参量共同作用的结果，改变单一参量并不能使传输性能最优.综合考虑各个因素对传输特性的影响，合理选择传输参量，才能最大程度地提升带宽性能.

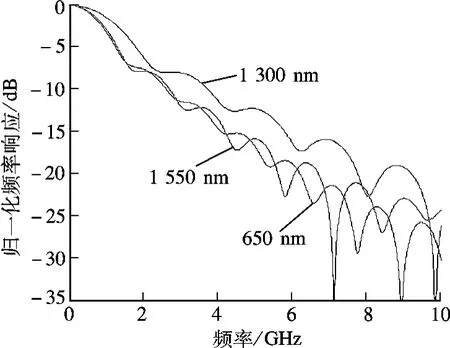
图7 不同工作波长下的频率响应对比

5 结语

PF－GIPOF 良好的物理特性和宽带特性使其成为短距通信的最佳传输介质.本文在任意折射率圆对称光纤传输参量计算的基础上，理论分析了传输特性，推导出基带功率传输函数，得到综合折射率指数、材料色散、光注入条件等因素的色散计算模型，仿真得到模群时延和模式损耗的分布特性，取不同参数计算频率响应和－3 dB 带宽.实验结果表明:DMA 在一定程度上可提高传输带宽，合理选择激励光源和光纤传输参量可有效提高系统的通信性能.该色散模型可用于任意条件下PF－GIPOF 传输参量和带宽的估算及仿真，为推动POF在数据通信等领域的应用奠定了理论分析和实验基础，具有一定的实用价值.

References)

［1］Palais J C.光纤通信［M］.王江平，等译.5 版.北京:电子工业出版社，2011:12－16.

［2］王云明，孙小菡，张明德，等.塑料光纤锥形过渡器光波传输特性研究［J］.东南大学学报:自然科学版，2002，32(3):351－354.

Wang Yunming，Sun Xiaohan，Zhang Mingde，et al.Study on performance of lightwave propagation in trapered polymer optical fiber connector ［J］.Journal of Southeast University:Natural Science Edition，2002，32(3):351－354.(in Chinese)

［3］Okonkwo C M，Tangdiongga E，Yang H.Recent results from the EU POF－PLUS project:multi－gigabit transmission over 1 mm core diameter plastic optical fibers［J］.Journal of Lightwave Technology，2011，29(2):186－193.

［4］Louvros S，Kougias I E.Attenuation and time dispersion measurements of graded index polymer optical fiber for indoor cellular coverage［J］.Contemporary Engineering Sciences，2009，2(2):47－58.

［5］Kurt T，Yongacoglu A，Chouinard J Y.OFDM and externally modulated multi－mode fibers in radio over fiber systems［J］.IEEE Transactions on Wireless Communications，2006，5(10):2669－2674.

［6］Yuen R，Fernando X N，Krishnan S.Radio over multimode fiber for wireless access［C］//Canadian Conference on Electrical and Computer Engineering.Ontario，Canada，2004，3:1715－1718.

［7］Garito A F，Wang J，Gao R.Effects of random perturbations in plastic optical fibers［J］.Science，1998，281(5379):962－967.

［8］Gasulla I，Capmany J.Transfer function of multimode fiber links using an electric field propagation mode:application to radio over fiber system ［J］.Optics Express，2006，14(20):9051－9070.

［9］Yabre G.Comprehensive theory of dispersion in gradedindex optical fibers［J］.Journal of Lightwave Technology，2000，18(2):166－177.

［10］Ge W P，Yin Z M，Liu J J.Numerical calculation of bandwidth of graded－index plastic optical fiber under selective mode excitation ［J］.Journal of Optical Communications，2005，26(4):168－170.

［11］Golowich S E，White W，Reed W A.Quantitative estimates of mode coupling and differential modal attenuation in perfluorinated graded－index plastic optical fiber［J］.Journal of Lightwave Technology，2003，21(3):111－121.

［12］Lethien C，Loyze C，Vilcot J P.Differential mode delay measurements of fluorinated graded index polymer optical fiber ［J］.Photonics Technology Letters，2008，20(18):1584－1586.

［13］Montero D S，Vazquez C.Analysis of the electric field propagation method:theoretical model applied to perfluorinated graded－index polymer optical fiber links［J］.Optics Letters，2011，36(20):4116－4118.

［14］Yabre G.Theoretical investigation on the dispersion of graded－index polymer optical fibers ［J］.Journal of Lightwave Technology，2000，18(6):866－877.