模拟隧道衬砌混凝土湿度演化规律

巴明芳 钱春香

(1 宁波大学建筑工程与环境学院，宁波315211)

(2 东南大学材料科学与工程学院，南京211189)

从地下结构混凝土的环境影响因素来看，地下混凝土一侧直接与岩土体或地下水接触，因此岩土体、地下水的渗透性破坏已成为水下混凝土结构耐久性研究的一项重要工作［1-2］.而在混凝土结构中迁移的水是硫酸根离子、氯离子等侵蚀性离子的载体［3-4］.水底隧道衬砌混凝土属于典型的低水胶比混凝土，自完成浇注后的水化耗水作用及向环境中扩散蒸发作用均会消耗孔隙中的水分，使得其自身相对湿度下降［5］.无论管片在完成拼装前还是在服役运营期间，其混凝土内部湿度的变化对其耐久性能的影响至关重要.近年来，已开展了很多基于水分扩散机理的混凝土内部相对湿度分布的研究.Bazant 等［6］研究了非饱和混凝土中湿度非线性扩散定律，提出了基于扩散机制的非线性湿度计算模型;Nilsson［7］对高性能混凝土中相对湿度的长期变化规律进行了研究;Parrott［8］研究了水泥类型和养护条件对混凝土干燥性能和渗透性能的影响;Ryu 等［9］研究了环境条件对相对湿度和相对湿含量的影响规律;Lee 等［10］研究了构件混凝土板内部湿度的变化规律;国内的张君等［11-12］基于湿度的传输机制，考虑到混凝土内部水化耗水作用的影响，建立了混凝土内部相对湿度分布的非线性模型.王新友等［13］综合论述了混凝土在不同环境条件下水分迁移机理与理论模型，指出了高性能混凝土必须考虑自干燥效应对非线性水分扩散方程的修正.

可看出，当前针对混凝土中水分非线性传输的机理模型研究较多，但考虑多种复合凝胶材料水化耗水作用的混凝土湿度分布规律的研究还十分有限.本文结合隧道衬砌高性能混凝土的生产养护和服役条件，考虑混凝土复合胶凝材料水化耗水作用，提出了地下隧道衬砌混凝土内部湿度演化规律的数值计算模型，并对模型进行验证.

1 试验

1.1 原材料

试验采用的胶凝材料为P·Ⅰ52.5 水泥(江苏联合水泥有限公司)、Ⅰ级粉煤灰(华能南京电厂)及S95 级矿粉(南京坤宇水泥复合材料有限责任公司);细集料是赣江中砂，细度模数为2.8;粗集料为二级配玄武岩，石子粒径分别为5～10 mm和10～20 mm，比例为35∶65;外加剂为聚羧酸系高效减水剂(东营瑞源特种建筑材料有限公司);黄砂和玄武岩石子密度分别为2 620 kg/m3和2 690 kg/m3.胶凝材料物理化学性能见表1.

表1 胶凝材料的化学组成及物理性能

1.2 试验方案

按照表2配合比制备尺寸为60 cm ×40 cm ×40 cm 的试件.其中，模板采用厚度为1.5 cm 的竹胶板制作，尺寸为60 cm ×45 cm ×45 cm，模板内衬是厚度为2.5 cm 的防水隔热卷材;除了试件的2 个40 cm ×40 cm 面外，其余各面均用防水热塑胶密封.混凝土拌制均匀，统一进行分层浇注，并沿着试件中长轴方向在距离干燥面分别为0，2，5，15，30 cm 处的O，A，B，C，D 五个测点直接预埋温湿度传感器.图1是浇注成型的衬砌混凝土湿度试验的实物图及相对湿度测量点的布置图.

为了能够保证混凝土浇注后立即可以进行温湿度测量，采用透水透气纤维纺布封住PVC 管埋入混凝土一端，把湿度传感器放入管中，将其引线处用防水胶布和硅胶密封，浇注混凝土试件的同时将其直接预埋在试件不同测量位置.5 个测点处的湿度传感器在使用之前均在饱和盐湿度发生器中进行了校正.将边长为100 mm 的混凝土试件放置在模拟试件旁边，并测量其内部湿度变化，用以对湿度测量结果进行标定.24 h 后把试件直接放在蒸养箱内，在(50 ±5)℃的条件下蒸养14 h 后，将蒸养箱内放入水并保持水温(20 ±2)℃，水养14 d后把水放掉，并使试件的其中一个40 cm ×40 cm成型面与大气直接接触，另一40 cm ×40 cm 面用饱水海绵包裹，模拟与管片外侧直接接触的保水土壤层，然后放置在室温内定期测量其内部相对湿度和温度的变化.

图1 衬砌混凝土内部湿度试验实物图及内部测定布置示意图(单位:cm)

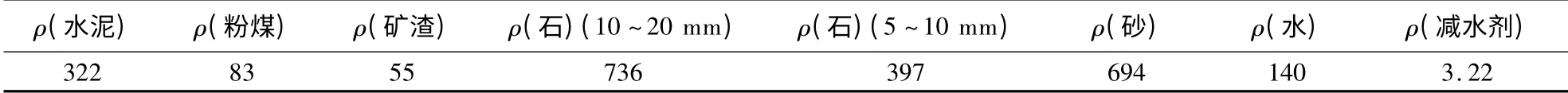
表2 混凝土配合比 kg/m3

2 结果分析与讨论

2.1 隧道衬砌混凝土温湿度时变规律的试验结果

2.1.1 相对湿度时变规律

图2为衬砌混凝土内部湿度变化的测量结果.从图2(a)可看出，在初始蒸养的14 h期间，由于蒸养温度及较高水化放热速度的影响，各个测点的相对湿度降低很快，并沿着O-A-B-C-D 的方向相对湿度降低速度增大，不过最低相对湿度一直在90%以上.从图2(b)可看出，结束水养之后，与空气直接接触的表面位置处相对湿度快速降低，并很快与室内相对湿度保持一致.距离与内空气接触的表面较近的A，B 两个测点的相对湿度随着时间的延长降低速度较快，至200 d 龄期时所对应的相对湿度均在87%～88%之间.距离表面较远处的C，D 位置处，相对湿度随着时间的延长变化较慢，200 d 龄期时，其相对湿度仍然保持在90%以上.

图2 衬砌混凝土内部相对湿度随时间的变化

2.1.2 内部温度时变规律

图3是混凝土内部O，A，B，C，D 五个测点处温度随着时间的变化结果.由图可见，管片内部各测点处温度的变化趋势与蒸汽养护箱内的温度变化趋势基本一致，在蒸汽养护结束的3 d 内管片内部各测点处的温度与环境温度相差不大，因此在对管片服役期间的湿含量进行数值分析时暂时忽略了温度的影响.

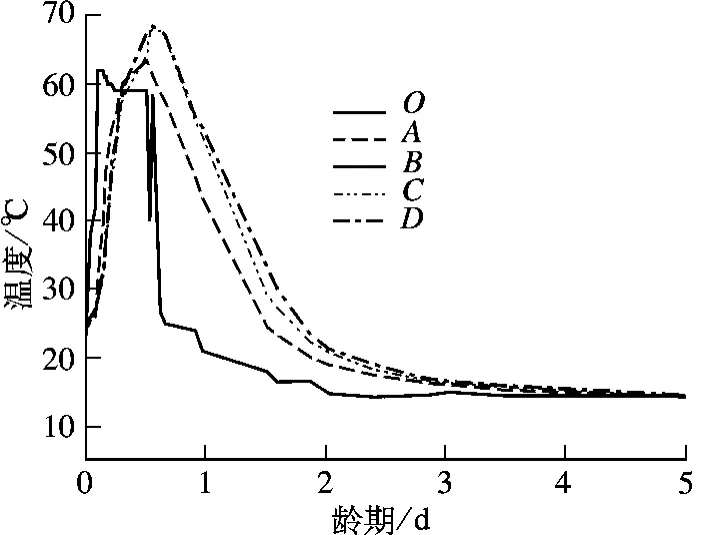
图3 衬砌混凝土内部温度变化

2.2 隧道衬砌混凝土湿度演化模型的建立

2.2.1 湿度演化模型的提出

地下隧道衬砌混凝土水胶比低，掺加了大量矿物掺和料，尤其是在完成浇注之后进行了一定时间的初始蒸汽养护，因此其内部湿含量分布主要取决于可蒸发水的扩散作用和复合胶凝材料的水化耗水作用.因此，完成拼装前衬砌混凝土的湿含量变化方程为

式中，w 为单方混凝土中可蒸发水体积含量，m3/m3;Deff(w)为湿含量有效扩散系数，m2/h;wd为扩散作用消耗的可蒸发水的体积含量，m3/m3;wh为胶凝材料水化所消耗的可蒸发水的体积含量，m3/m3.

完成拼装之后衬砌混凝土迎水面直接与地下饱水土层接触，一定水压力作用下的渗透作用不容忽视，因此该阶段的衬砌混凝土内部湿含量的变化方程为

式中，p 为衬砌混凝土水压力，Pa;Kp为混凝土渗透系数，m/h;ρw为水的密度，kg/m3.

根据文献［2］研究结果，水压力作用下的渗透作用只影响地下结构混凝土迎水面很薄的一层，因此，这里对江底隧道混凝土湿度演化规律的研究可直接按照式(1)进行研究.

2.2.2 复合胶凝材料水化耗水方程的确定

掺加矿物掺和料的混凝土，不仅水泥水化消耗水分，矿物掺和料的水化同样会引起可蒸发水含量的减少，因此某龄期单方混凝土胶凝材料水化作用所消耗的可蒸发水体积含量为

式中，mc为单方混凝土中水泥的质量，kg/m3;mf为单方混凝土粉煤灰质量，kg/m3;ms为单方混凝土矿粉质量，kg/m3;wc为单位质量水泥完全水化需要消耗的可蒸发水量，kg/kg;wf为单位质量粉煤灰完全水化需要消耗的可蒸发水量，kg/kg;ws为单位质量矿粉完全水化需要消耗的可蒸发水量，kg/kg;αc(t)，αf(t)，αs(t)分别为某龄期t 时水泥、粉煤灰及矿渣微粉的水化程度.

根据Powers 水化理论［14］，每1 g 水泥水化反应中要结合水0.25 g，吸附水0.15 g 及凝胶水0.02 g，因此wc=0.42;根据Wang 等［15］对矿物掺和料水化耗水的研究可知，1 g 粉煤灰完全水化需要结合水0.10 g，凝胶水0.15 g，故wf=0.25;1 g矿粉完全水化需要结合水0.30 g，凝胶水0.15 g，所以ws=0.45.因此式(3)可调整为

把文献［14］提出的胶凝材料动力学关系式代入式(4)，可得混凝土复合胶凝材料水化耗水方程为

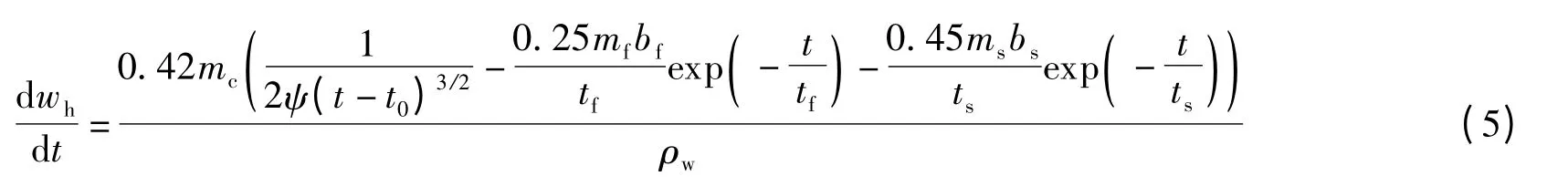
2.2.3 定解条件的确定

1)衬砌混凝土服役前的定解条件

初始湿含量等于单方混凝土用水的体积分数.由于该阶段水分会通过毛细孔隙进入到衬砌混凝土内部，并使得该阶段衬砌混凝土毛细孔均处于水饱和状态.因此该阶段衬砌混凝土各位置处的湿含量大小恰好等于混凝土的毛细孔隙率.将文献［16］中衬砌混凝土毛细孔隙率时变方程代入，可得到该阶段任意时刻的湿含量为

2)衬砌混凝土服役后的定解条件

衬砌服役后隧道内部风速较高，混凝土表面水分的蒸发速度很快，在衬砌混凝土表面形成温湿度变化明显的过渡区空气层，称为近表面层;由于混凝土水胶比较低，完成水养之后结构已相当密实，根据文献［17］，在计算时取近表面层厚度为固定值25 mm.所以这里以混凝土湿度试验试件在位置O 处的测量结果作为湿含量方程的上边界条件(x=x0)，即

考虑到隧道外侧某些防水难以处理的部位或可能会出现漏水的部位混凝土与地下饱水土层直接接触的情况，因此该边界上衬砌混凝土湿含量与其毛细孔隙率近似相等.在隧道水压力作用下的水由迎水面以饱水状态向内部渗透，因此该阶段与饱水土层相接触的下边界条件(x =l)为混凝土时变毛细孔隙率，即

2.3 湿度分布模型数值计算与试验结果的对比分析

由于Crank-Nicolson 格式对任意步长比均是稳定的和收敛的，从计算量的角度来分析，要想获得同样精度的解，采用Crank-Nicolson 格式比用其他格式计算量也少很多.因此这里对非线性湿传输方程(1)的求解过程是:建立Crank-Nicolson 格式的差分方程，同时采用前一层的数值来表示非线性湿含量传输方程(1)中非线性相Deff(w)，以建立线性化的差分格式.具体过程如下:将记作g(t)，Deff(w)记作Deff(w)=C1w2+C2w +C3，并假设空间和时间等分数分别为M，N，空间步长h=0.6/M，时间步长τw=t/N，那么空间节点分别为x0，x1，x2，…，xM－1，xM，时间节点分别为t0，t1，t2，…，tN－1，tN.

记

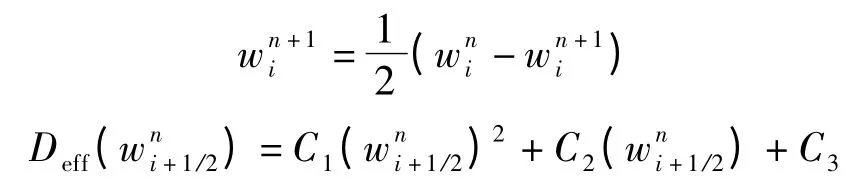
因此

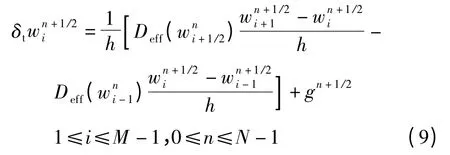
记s =τ/h2，将式(9)展开得

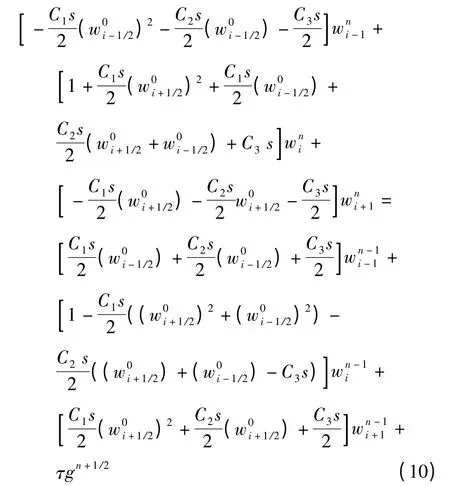
式(10)中每一层只需用追赶法求解一个M－1阶的三对角方程组，在计算过程中利用求得的w 值来判断是否发生水化，即当w 低于80%相对湿度所对应的湿含量时，令g(t)=0 即可.图4是M =30，N=1.6×105时试验结果与计算结果的对比.

图4 湿含量试验与计算结果对比分析

由图4可看出，在距离与大气相接处的上边界不远的位置处，隧道衬砌混凝土内部湿含量变化较快;而与饱水土层相接处的下边界附近，由于水化作用而导致的阶梯型的湿含量梯度也比较明显.在距离蒸发面比较近的100 mm 处，衬砌混凝土内部湿含量变化受扩散影响较大，在距离蒸发面较远的位置处湿含量随时间的变化主要是由于胶凝材料水化耗水所致.

从图4还可看出，5 个测点处湿含量的数值计算结果与测量结果相差不大，并且其变化趋势基本一致，这说明可采用本文所提出的湿度传输模型对隧道衬砌混凝土湿度分布进行预测.图5是所研究隧道衬砌在10年内绝对湿度分布的数值计算结果.可看出，在模拟隧道衬砌服役3 600 d 时，距离蒸发面距离为100 mm 以内的部分湿含量状态均与环境湿度状态达到平衡.还可看出，当管片设计保护层厚度为20 mm 时，服役1 600 d 后保护层内部湿含量与隧道内部大气中湿度条件达到平衡.在前期湿度梯度主要是集中在距离隧道内部大气蒸发面较近的管片区域，而随着服役年限的延长，管片内部湿度梯度逐渐向饱水面推进.这说明，前期湿度变化主要是受上边界干燥面混凝土中水分蒸发速度的影响，而随着时间的发展，湿度变化则主要是由饱水面与蒸发面处的湿度梯度所致.

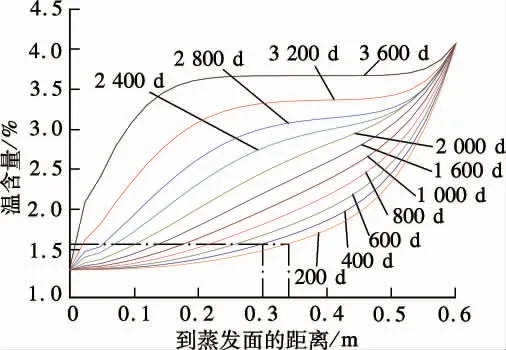
图5 湿含量时域分布的数值计算结果

3 结论

1)提出了基于水分扩散、水化耗水及水渗透作用的地下隧道衬砌混凝土的湿含量分布模型.采用有限差分的方法对湿含量非线性时空分布进行了数值解析.对计算结果与试验结果进行了比较分析，结果表明，建立的湿度分布计算模型可以很好地对地下衬砌混凝土的湿含量分布特征进行预测和分析.

2)湿度演化模型预测结果说明，在距离衬砌蒸发面比较近的100 mm 处，混凝土内部湿含量变化受扩散影响较大，在距离蒸发面较远的位置处，湿含量随时间的变化主要是由于胶凝材料水化耗水所致;随着地下衬砌混凝土服役年限的延长，其内部湿度梯度逐渐向饱水面推进.

References)

［1］Brown P W，Doerr A.Chemical changes in concrete due to the ingress of aggressive species ［J］.Cement and Concrete Research，2000，30(3):411-418.

［2］Qian C X，Wang Y J，Huang B.Sewage law of water in concrete ［J］.Journal of Construction Materials，2009，5(12):515-518.

［3］Ye G.Percolation of capillary pores in hardening cement pastes ［J］.Cement and Concrete Research，2005，35(7):167-176.

［4］Martys N S，Ferraris C F.Capillary transport in mortars and concrete ［J］.Cement and Concrete Research，1997，27(5):747-760.

［5］Oh B H，Cha S W.Nonlinear analysis of temperature and moisture distributions in early-age concrete structures based on degree of hydration［J］.ACI Materials Journal，2003，100(5):361-370.

［6］Bazant Z P，Najjar L J.Nonlinear water diffusion in non-saturated concrete ［J］.Materials and Structures，1972，5(25):3-20.

［7］Nilsson L O.Long-term moisture transport in high performance concrete［J］.Materials and Structures，2002，35(254):641-649.

［8］Parrott L J.Influence of cement type and curing on the drying and air permeability of cover concrete［J］.Magazine of Concrete Research，1995，47(171):103-111.

［9］Ryu D W，Ko J W，Nouchi T.Effects of simulated environmental conditions on the internal relative humidity and relative moisture content distribution of exposed concrete［J］.Cement and Concrete Composites，2011，33(1):142-153.

［10］Lee C J，Lange D A，Liu Y S.Prediction of moisture curling of concrete slab［J］.Materials and Structures，2011，44(4):787-803.

［11］Zhang J，Qi K，Huang Y.Calculation of moisture distribution in early-age concrete ［J］.Journal of Engineering Mechanics，2009，135(8):871-880.

［12］Zhang J，Hou D W，Gao Y，et al.Determination of moisture diffusion coefficient of concrete at early age from interior humidity［J］.Drying Technology，2011，29(6):689-696.

［13］王新友，蒋正武，高相东，等.混凝土中水分迁移机理与模型研究评述［J］.建筑材料学报，2002，5(1):66-71.

Wang Xinyou，Jiang Zhengwu，Gao Xiangdong，et al.Review on the mechanism and model of moisture transfer in concrete［J］.Journal of Building Materials，2002，5(1):66-71.(in Chinese)

［14］Powers T C.A discussion of cement hydration in relation to the curing of concrete［J］.Highway Research Board Proceedings，1947，27:178-188.

［15］Wang X Y，Lee H S.Modeling the hydration of concrete incorporating fly ash or slag ［J］.Cement and Concrete Research，2010，40(7):984-996.

［16］Ba M F，Qian C X.Evolution of capillary porous structure in steam curing concrete with mineral admixtures［J］.Advanced Materials Research，2012，450-451:3-7.

［17］李春秋，李克非，陈肇元.混凝土中水分传输的边界条件研究［J］.工程力学，2009，26(8):74-81.

Li Chunqiu，Li Kefei，Chen Zhaoyuan.Research on water transmission boundary condition in concrete［J］.Engineering Mechanics，2009，26(8):74-81.(in Chinese)