改进贝叶斯聚焦的宽带自适应单脉冲算法

陈 亮 盛卫星 韩玉兵 马晓峰

（南京理工大学电子工程与光电技术学院，江苏 南京210094）

引 言

数字波束形成技术以其灵活的多波束性能和强抗有源干扰性能在雷达、声纳、无线通信等领域得到了广泛应用.随着技术的发展，为提高距离分辨能力和成像分辨率，一些先进雷达系统的带宽越来越宽，宽带数字波束形成成了阵列天线和阵列信号处理领域的一个研究热点.

过去十几年来，对于宽带波束形成的研究，学者们做出了很多的努力，并且取得了一定的成果.例如，有学者提出利用空时联合的自适应处理方法［1-4］，通过在每一个天线单元后增加一个有限长单位冲激响应滤波器，提高系统的自由度，来实现宽带数字波束形成.有的学者提出了利用Bessel函数展开的方式实现宽带波束形成［5］.有的学者提出了将宽带波束形成问题转换为一个凸优化问题，通过设计个性化的代价函数，并利用现有的凸优化解决工具，实现宽带数字波束形成［6-7］.近几年来，相干信号空间聚焦类算法［8-11］由于相对适中的运算量以及较好的性能得到了众多学者的广泛关注，酉约束阵列导向矢量聚焦（Unitary Constrained Array Manifold Focusing，UCAMF）［8］、旋转信号子空间（Rotational Signal Subspace，RSS）［9，11］、双 边 相 关 变 换（Two-sided Correlation Transformation，TCT）［10］等聚焦算法相继被提出.然而，上述算法的最大缺点在于，聚焦矩阵的计算是建立在期望信号以及干扰来波方向先验已知的条件下的.如果预计的期望信号及干扰角度来向信息与实际的角度来向存在偏差，那么聚焦算法的性能将急剧下降，从而影响到最终的宽带波束形成性能.

目前，窄带自适应单脉冲算法的研究成果比较丰富［12-14］，而针对宽带自适应单脉冲算法的研究并不是很多.Bucris在文献［15］中提出了基于Bayesian聚焦的宽带数字波束形成算法.该算法假设期望信号和干扰信号的来波方向服从正态分布，在一定范围内，克服了角度先验估计误差对最终波束形成性能的影响.在此基础上，本文针对单脉冲雷达实际工作环境中的具体情况，重新设计聚焦矩阵，提出了改进算法.一方面，该算法进一步降低了系统对先验信息的要求，增强了算法的普遍性和实用性；另一方面，在保证和波束性能的情况下，该算法克服了传统Bayesian方法不能直接被应用到差波束求解上的缺陷.

1 宽带阵列信号模型

宽带信号可以被看作是若干相邻频率窄带信号的组合，以简化分析.假设宽带信号s（n）是由J个窄带信号叠加而成的，即

式中：sfj（t）是以fj为中心频率的窄带信号成分的时域采样.对式（1）中的每一个窄带信号运用窄带阵列信号模型，那么宽带信号下的阵列接收数据可以写成

式中：a（fj，θ）表示fj频率下，来波方向为θ的阵列流形矢量；n（t）表示噪声信号，它也可以被写成J个窄带噪声信号之和为

将式（3）代入式（2）可以得到

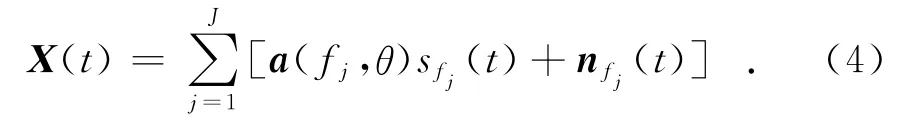
当有 K 个远场信号s1（t），s2（t），…，sK（t）分别来自θ1，θ2，…，θK方向的时候，总的阵列输出宽带信号可以表示为

式中：A（fj，θ）＝［a（fj，θ1），a（fj，θ2），…，a（fj，θK）］；Sfj（t）＝［s1，fj（t），s2，fj（t），…，sK，fj（t）］T.从式（5）可以看出，该数据模型和窄带阵列数据模型是非常相似的.

2 传统聚焦算法的基本原理

相干信号子空间类方法，对接收到的数据进行快速傅里叶变换处理，将宽带接收信号划分为若干个互不重叠的窄带子频率带，对每个窄带子频率带内的数据进行聚焦处理，将它们聚焦到预先设定的参考频率上.接着，算法对聚焦之后的协方差矩阵求平均，从而减小了信号之间的相干系数，达到了解相干的目的.其核心思想实际上就是频域平滑技术.对于宽带自适应波束形成来说，利用经过了聚焦处理和平均之后的协方差矩阵，在参考频率点上，进行经典的窄带自适应波束形成算法，就能实现宽带的自适应波束形成.整个算法的结构框图如图1所示.

如何构造聚焦矩阵就成为此类算法的关键问题.不同的聚焦矩阵选取对应不同的算法，其核心思想都是在某种准则下，找到聚焦频点和参考频点之间的某种关系.文献［9］构造如下的代价函数：

式中：T（fj）表示聚焦频率为fj时对应的聚焦矩阵；A（f0）和A（fj）分别表示参考频率和聚焦频率下对应的阵列流形矢量.为了简洁，文后都用A（f0）和A（fj）代替A（f0，θ）和A（fj，θ）.该算法即为 RSS算法，其核心思想是使各频点聚焦后的阵列流形矢量和参考频率下的阵列流形矢量之间的误差最小.文献［10］构造了如下所示的代价函数为

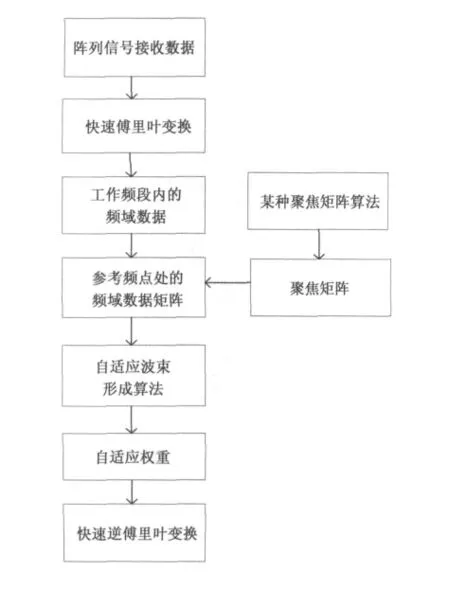
图1 相干子空间类方法整体框图

式中：

该算法就是TCT算法，其导出的聚焦矩阵是使各频率点聚焦后并且去噪的协方差矩阵与参考频率处去噪后的协方差矩阵之间的误差为最小.

其它的相干聚焦算法还包括总体最小二乘算法，信号子空间变换算法等.但是，这类算法要么就是必须要精确地知道信号和干扰的来向，要么就是直接的数据域求解，微小的来向估计误差会带来很大的聚焦误差，从而导致波束形成算法性能的下降，而直接的数据域求解又带来巨大的计算量.这些短板限制了此类算法的应用.

3 改进的Bayesian聚焦算法

针对传统聚焦算法在来波方向估计存在误差的情况下，性能恶化的事实，文献［15］提出了基于Bayesian聚焦的宽带波束形成算法.

考虑到信号和干扰来波方向的不确定性，最优聚焦矩阵可以通过如下方法获得

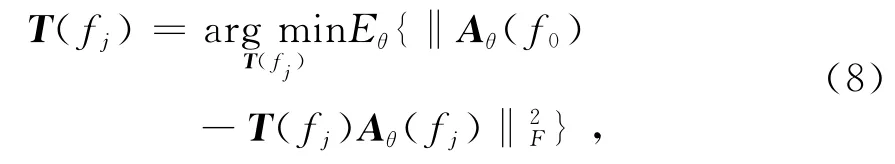
式中：T（fj）表示聚焦频率为fj时对应的聚焦矩阵；Eθ｛·｝表示对按某一规律随机分布的来波方向角求数学期望；f0和fj分别表示参考频率和聚焦频率；‖·‖2F表示二范数的平方.假设共有K个远场信号，并且各自的来波方向呈随机分布且相互独立，可得

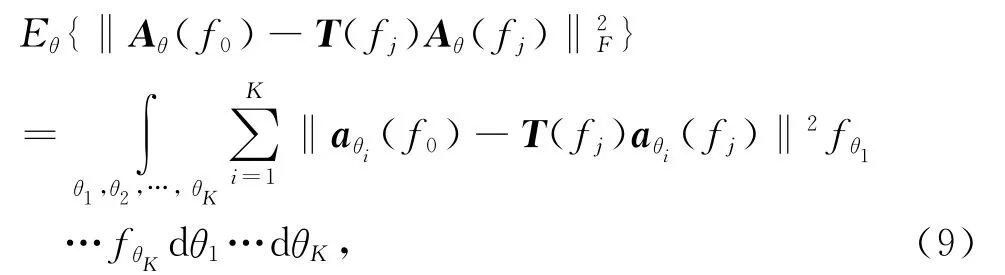
式中：aθ（fj）表示来波方向为θ，频率为fj情况下的阵列流形矢量；fθi表示第i个远场信号来波方向的概率密度函数.由于各个来波方向角相互独立，式（9）就可以转换为一个一重积分的求解问题，从而简化了聚焦矩阵的计算，具体步骤如下：

定义：

可以看出，p2（θ）反映出的是K个远场信号来波方向不确定性的总体表征.将式（10）、（11）代入式（8）中，得

式（12）就是Bayesian聚焦矩阵求解的核心公式.从上面的分析可以看到，聚焦矩阵求解的基本思想就是：在考虑来波方向不确定因素的情况下，使得聚焦前后的阵列流形矢量误差的期望值为最小的那个聚焦矩阵，就是最优解.不同的来波方向概率密度函数对应不同的聚焦算法.比如说，当来波方向概率密度函数满足在观察角度范围内均匀分布的时候，对应全局聚焦算法；当来波方向概率密度函数满足在某些角度上出现为必然事件，而在其余角度位置上出现为不可能事件的时候，对应旋转信号子空间（RSS）算法.

为了求解式（12）中的最优聚焦矩阵，首先求解一个特殊情况，也就是来波方向概率密度函数为均匀分布下的解.根据文献［16］可以知道，任一频点下的阵列流形矢量都可以用一组正交基函数的线性组合表示，如果采用傅里叶基函数的话，有

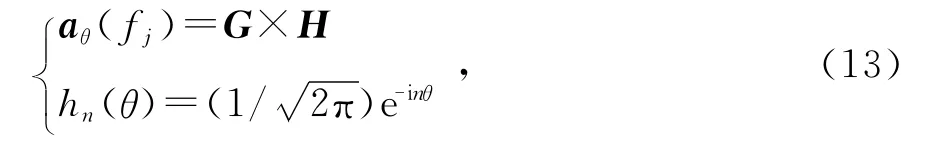
式中：G为基函数系数矩阵；H为基函数矩阵；hn（θ）即为H中的第n行元素.在不考虑阵元间互耦以及假设阵元具有全向性的时候，G的第m行第n个元素可以表示为

式中：（θm，rm）是第m阵元位置的极坐标表示；Jn（·）表示n阶第一类Bessel函数.如果式（13）中采用的正交函数基为N阶的话，那么G为一个M×（2 N＋1）的矩阵，而H为一个（2 N＋1）×1的矩阵.式（14）中n的变化范围是 -N到N.

由上面的分析可知，该频点下的聚焦误差可以重新写成

式中，Gθ（f0）表示参考频点下的G矩阵.经推导可以得到，此时的最优聚焦矩阵为

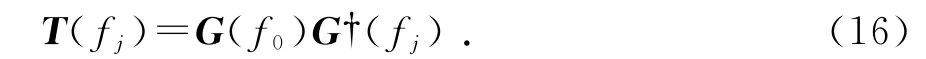
式中‘†’表示矩阵伪逆.

文献［13］考虑来波方向的不确定性，结合其概率密度函数，利用上述思想，令

由式（13）和（17）可以看出，Bayesian方法相比于全局聚焦方法，区别仅仅在于导向矢量前的加权函数p（θ）的不同.经过简单的数学推导可以得到

式中

由式（18）可以看到，新基函数系数矩阵C可以被看作是ρ矩阵和G矩阵的卷积.其中，Cmn是系数矩阵C的第m 行n列元素.式（19）中，ρ矩阵表示对式（11）中的p（θ）做正交基函数分解得到的系数矩阵，ρn为ρ矩阵的第n个元素.

类似式（16）可以得到此时的最优聚焦矩阵为

如前所述，不同的概率密度函数对应具体不同的聚焦算法.文献［15］着重考虑和波束性能，提出期望信号来波方向和干扰来波方向均服从正态分布的假设，即

式中：θ1和θ2为假设的期望信号和干扰来波方向的平均值；σ1和σ2分别为标准差.当期望信号以及干扰信号的实际来波方向与预计的期望值差别不大的时候，该算法具有比较低的聚焦误差，而这种性能的获得是以增加大偏离角下的聚焦误差换来的.所以，此种概率密度函数的假设，同样具有一定局限性.

对单脉冲角度跟踪下的应用.传统的Bayesian算法并不能直接应用在差波束上，这并不是由自适应波束形成算法所造成的，而是聚焦算法本身的问题，所以，文后对此问题的分析都是建立在非自适应波束形成的基础上的.

理想的情况是没有任何聚焦误差的情况，为了简化分析，假设阵列为一个均匀线阵，阵元个数为偶数，选取阵列中心的位置为参考.经过聚焦处理之后，宽带信号某一频点下非自适应的静态单脉冲比，就完全和窄带条件下非自适应的静态单脉冲比相同，可以按照如下公式表示为

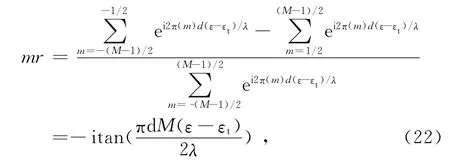
式中：ε和εt分别表示实际角度和指向角度对应的方向余弦；d和λ分别表示阵元间距和波长.如果实际情况中包含聚焦误差的话，那么被聚焦误差“污染”了的单脉冲比可以表示为

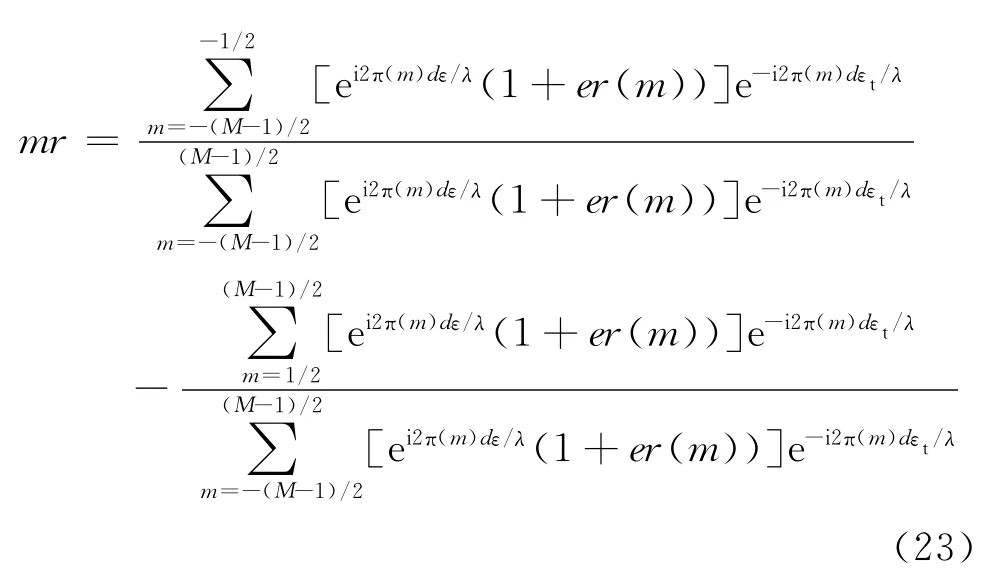
式中er（m）表示第m个阵元对应的聚焦误差.因为只有分子对差波束起作用，可将式（23）中分子上的误差部分单独取出为

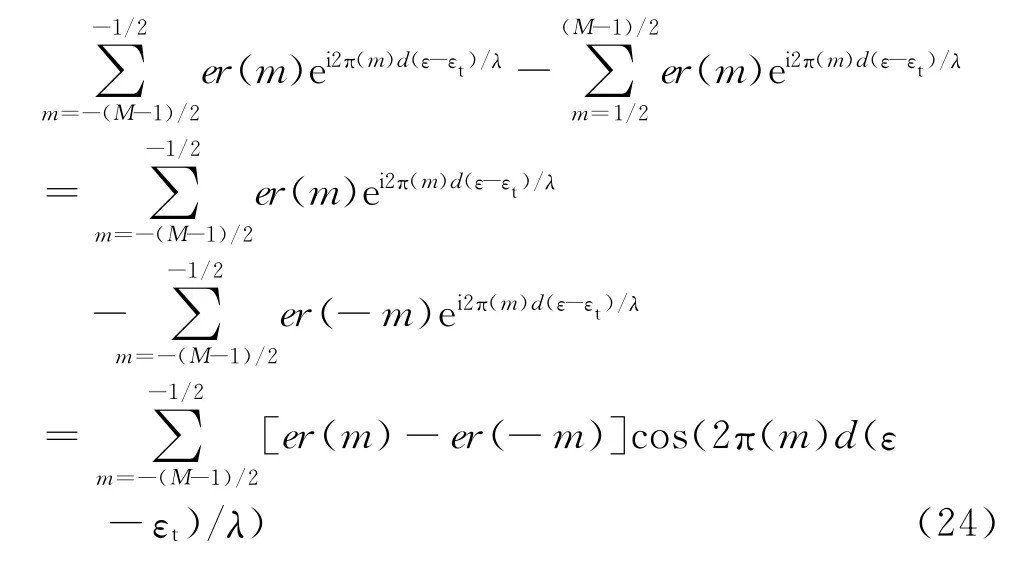
从式（24）可以看到，当聚焦误差在阵元上呈现对称分布特性的时候，也就是er（m）＝er（-m）的时候，误差部分对差波束产生的贡献基本接近于0.

考虑到全局聚焦方法［17］在整个角度域内，具有相对比较平坦的聚焦误差分布，并且聚焦误差在阵元上的分布具有对称特性，有利于对称取反法下自适应差波束的求解.同时，传统Bayesian方法下的和波束又具有较好的干扰抑制性能，将上述两种方法的思想结合起来，给出如下的概率密度函数假设

式（22）假设期望信号来向服从均值为θ1，标准差为σ1的正态分布，而干扰信号方向假设服从平均分布.其中Δθ为干扰信号来波方向平均分布的范围.

干扰信号的来波方向范围估计方法如下：

首先，在时间域上对接收到的阵列信号进行相干累加，降低噪声成分，即

遍历整个角度范围，通过对感兴趣频带上的静态波束形成结果进行累加，得到整个角度遍历结果，即.

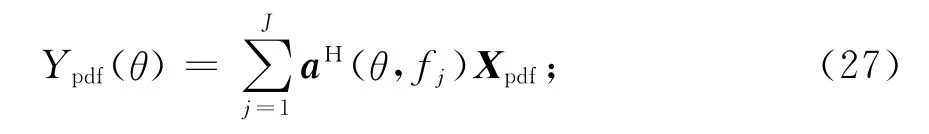
通过设置合适的门限值，判断上一步中的结果.如果对应某个角度下的值大于门限，就认为该处出现干扰的可能性比较大，反之则认为不可能出现干扰.概率密度函数可以表示为

假设不仅降低了算法对先验知识的要求，不需要任何干扰信号来波方向的先验知识，增加了整个系统的灵活性，从文后的仿真实验可以看出，提出的改进方法，在改善和波束性能和稳健性的同时，解决了大偏差角下的大聚焦误差问题，比全局聚焦方法和传统Bayesian聚焦方法更具优势，从而被成功地运用到宽带自适应差波束的求解上.

在上述基本原理的基础上，给出整个算法的基本原理.通过上面的分析可知，经过聚焦处理后的数据协方差矩阵为

那么，总的协方差矩阵为各个频点上被聚焦后的协方差矩阵的和为

和、差波束均采用线性约束最小方差（Linearly Constrained Minimum Variance，LCMV）准则，该准则的核心思想是：在满足期望方向恒定增益约束的同时，使得总的输出功率最小，从而对干扰信号起到抑制作用，即

式中：w表示待求解的权重系数矢量；c为约束导向矢量，对于宽带波束形成来说，通常将其设定为参考频率下，期望方向的阵列流形矢量；f为约束响应矢量，用来保证期望方向上的增益值.

对和波束形成来说，c＝a（θ，f0），θ和f0分别表示期望信号的来波方向以及参考频率.如前所述，对称取反法下，差波束对应的约束导向矢量为和波束下约束导向矢量的前一半元素不变，后一半元素取相反数，即

式中：符号‘·’表示哈达玛乘积.取这样的导向矢量的目的，实际上是为了在干扰方向形成零陷的同时，在差波束方向图对应期望信号方向上产生零深.利用拉格郎日乘数法可以得到式（31）的解为

至此，我们给出算法的具体步骤：

1）通过阵列接收数据，利用式（25）、（27）和（28），估计出外界干扰来波方向的概率密度函数分布，并进而构造p2（θ）.

2）在给定的基函数阶数及阵列结构下，利用式（14）计算得到矩阵G.

3）利用式（18）和（19），计算系数矩阵C.

4）利用式（20），计算各个频点下的聚焦矩阵T（fj）.

5）利用式（29）和（30）计算经过频域平滑后的数据协方差矩阵R.

6）根据式（32）和式（33），计算和、差波束权重系数矢量w.

4 计算机仿真及分析

仿真参数设置如下：实验采用均匀分布线阵，阵元间距为信号最大频率对应波长的一半，阵元数目为20个；期望信号和干扰信号都采用线性调频的形式，中心频率为1 500Hz，带宽为600Hz，参考频率为1 500Hz，相对带宽为40%；信号快拍数为256；噪声功率为1.为突出文章中提出算法的优越性，将所提改进方法对应的仿真结果和传统Bayesian方法［15］、RSS聚焦方法［9］以及全局聚焦方法［17］的结果进行比较.

4.1 干扰信号来波方向的概率分布估计

需要对干扰信号来波方向的概率密度函数进行合理的估计，结果如图2所示.

式（25）中的门限值被设为扫描结果最大值的0.9倍.从图2可以看到：在实际的干扰信号来波方向为70°的情况下，估计得到的干扰信号来波方向的概率密度函数服从60°度到80°范围内的均匀分布.后面的仿真中，均假设干扰信号来波方向服从该概率密度函数.

4.2 输出信干噪比随输入信噪比变化实验

本实验给出了各种方法下，和波束输出信干噪比随输入信噪比的变化曲线.图3给出了DOA估计误差较小的时候，输出信干噪比随输入信噪比的变化.

假设期望信号来自105°，干扰信号来自70°，干扰噪声比为40dB.传统Bayesian方法中，两正态分布函数的均值分别是105°和70°，恰好对准实际信号和干扰来向，标准差均设置为1.5.改进方法中的正态分布函数均值为105°，方差也为1.5，和传统方法中的设置一样.可以看到，低信噪比条件下，RSS算法性能相对要比其它算法好一点，原因在于信号实际来波方向和假设的方向是完全对准的，因而具有最优的性能，其余算法性能基本相当.当信噪比比较高的时候，改进Bayesian方法具有比较好的性能，而其余方法性能有明显的下降.

图3 DOA估计误差较小时，输出信干噪比随输入信噪比的变化

图4给出了DOA估计误差较大的时候，输出信干噪比随输入信噪比的变化.这里，信号方向仍然被设定为105°，而干扰方向被设定成60°.此时，由于比较大的来波方向估计误差，RSS聚焦方法下的波束形成性能急剧下降，完全起不到自动抑制干扰的目的.传统Bayesian尽管在一定程度上抑制了干扰，但是整体效果不如文中提出的改进Bayesian方法.而全局聚焦方法本身与期望信号和干扰信号的来向没有关系，所以其结果也和图3中的类似，在高信噪比条件下性能明显下降.

图4 DOA估计误差较大时，输出信干噪比随输入信噪比的变化

综合图3和图4的结果，可以看到，文中提出的改进方法，能够充分利用阵列接收到的信号，波束形成性能稳健，对外界干扰环境的变化不敏感，保证了输出信干噪比性能.

4.3 和、差波束方向图实验

本实验信噪比为0dB，干噪比取40dB.和、差波束均采用LCMV波束形成算法.结果如图5和图6所示.

从图5可以看到：各个方法下的和波束方向图都能自动地将主瓣对准期望信号方向，在干扰方向上产生零陷.然而，相比于其他聚焦方法，传统的Bayesian聚焦算法在大角度估计误差下，方向图和参考频点下的方向图之间的偏差比较大.方向图边缘部分的发散也就更大.

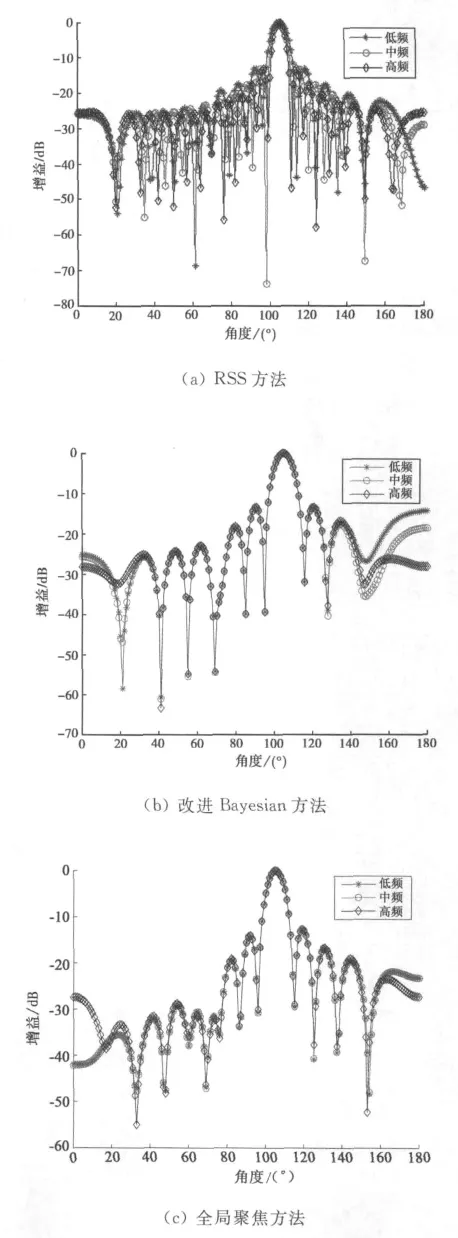
从图6可以看到：虽然各个方法下的自适应差波束方向图都能在干扰方向产生零陷，但是由于大角度偏差带来大估计误差问题，以及误差的非对称分布，导致传统Bayesian聚焦方法和RSS算法在期望信号指向位置没有能够产生零深，并且方向图畸变，旁瓣电平明显上升.

4.4 聚焦误差随角度变化实验

图7给出了各种不同聚焦算法下，各个不同频点下，聚焦误差在整个角度域内的变化情况.观察频点为最小频率（1 200Hz），中心频率（1 500Hz），测试频率（1 350Hz）和最大频率（1 800Hz）.

从图7可以看出：RSS聚焦算法只有在70°和105°两个位置具有比较小的聚焦误差，这也就解释了不同频率下的和波束方向图图5（a），差波束方向图图6（a）仅仅在期望信号和干扰信号这两个位置重合，而其余位置上均不重合的原因.全局聚焦算法在整个角度域内的分布相对比较平坦.传统Bayesian方法在70°和105°附近的聚焦误差很小，其他角度位置上，聚焦误差则迅速上升，并且在70°和105°之间的角度范围内，聚焦误差曲线有“凸起”.改进方法则具有比较好的聚焦性能，相比与全局聚焦方法和RSS方法，在70°和105°位置，其具有更小的聚焦误差.而相比于传统Bayesian方法，其“凹口”更宽，稳健性更好.

图7 各个方法下聚焦误差随来波角度的变化

4.5 聚焦误差在阵元上的分布实验

本实验研究了1 350Hz下，聚焦误差在阵元上的分布情况.结果由图8给出.

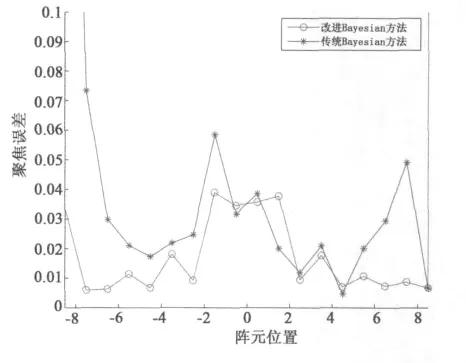
图8 聚焦误差在阵元位置上的分布

从图8的结果可以看出，改进方法下，聚焦误差在整个阵元上的分布基本呈现出对称的特性.而传统Bayesian方法下的聚焦误差在阵元上的分布不具有规则性.这也应证了式（24）要求的误差分布具有对称性的理论推导.观察图8可以进一步发现：阵列最两端处的阵元，其对应的聚焦误差是比较大的，可以理解此阵元在进行波束形成的时候是“失效”的.这种“失效”，导致系统实际的自由度会有所减少，从而使和波束方向图主瓣略有展宽，这也与图5中的结果吻合.

4.6 单脉冲测角误差实验

图9给出了各个方法下，自适应单脉冲比曲线的比较.可以看出RSS方法下，单脉冲比曲线产生了明显的畸变，而传统Bayesian方法更是出现了明显的零点漂移.全局聚焦算法与前二者相比，稳定性有所提高，但单脉冲比曲线也存在随频率发散的问题.文中提出的改进Bayesian方法，单脉冲比曲线线性特性好，零点对准期望指向，不随频率的变化而发散，具有较好的跟踪性能.

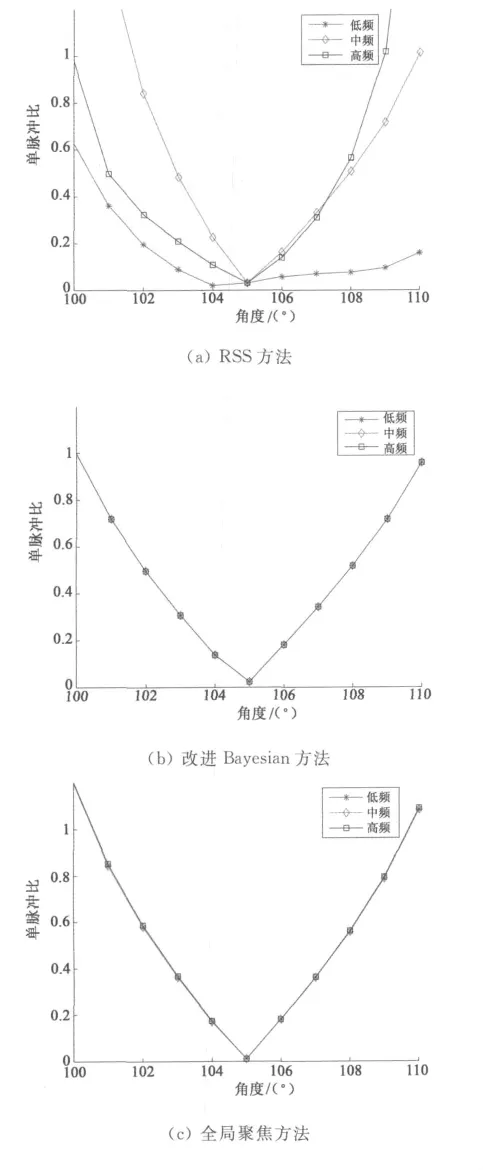
图9 各个方法下自适应单脉冲比曲线

图10给出了在改进方法下，自适应单脉冲测角误差随着输入信噪比变化的情况.可以看到，随着输入信噪比的增加，单脉冲跟踪的角度误差在逐步减小，当输入信噪比增大到一定程度之后，角度估计误差保持稳定，并最终收敛在一个接近于0的值上.因为自适应波束形成算法只能对有源干扰信号进行抑制，而没有办法滤除噪声信号，所以最终角度估计误差的值也只能收敛到一个非常接近0的地方，而不能够达到绝对0值.图10反映出来的结果，也从另外一个方面验证了提出的方法运用到自适应单脉冲的正确性和可靠性.

图10 改进方法下单脉冲测角均方根误差随输入信噪比变化

4.7 算法复杂度比较

文章所提方法、传统Bayesian方法、RSS聚焦方法以及全局聚焦方法的运算量在本节中进行比较.由于无论是哪种方法，都需要对各个频点下的聚焦矩阵进行计算，所以，这里给出上述几种方法的运算复杂度都是针对一个频点的，并且以复数乘法（Complex Maltiply，CM）的次数来衡量.

假设阵元个数为M，信源个数为K，来波方向概率密度函数正交分解的阶数为P，来波方向概率密度函数角度采样点的个数为Na，Bessel函数分解的阶数为Nb，快拍数为Ns.

RSS聚焦方法总共分为三个步骤，1）At＝Aθ（fj）Aθ（f0）H需要KM2次CM；2）对上式的结果进行奇异值分解，需要20 M3次CM；3）T＝VUH，需要M3次CM，所以总共需要21 M3＋KM2次复数乘法运算.

传统Bayesian方法总共分为三个步骤，1）如式（19）所示，对来波方向概率密度函数进行正交分解，需要（2P＋1）Na次CM；2）按照式（18）计算C（fj，ρ（θ）），此步骤需要（2 Nb＋1）（2P＋1）M 次 CM 运算；3）按照公（20），对聚焦矩阵进行计算，此步骤需要20 M3次CM运算；所以该方法总共需要20 M3＋（2P＋1）（2 MNb＋Na＋M）次CM.

全局聚焦方法只需要进行一次矩阵伪逆运算和一次矩阵乘法，总共需要20 M3＋（2 Nb＋1）M2次CM.

文中所提出的改进方法以传统的Bayesian方法为框架，所以基本的运算复杂度和传统Bayesian方法相同，只是多出式（27）所示的对来波方向概率密度函数的更新操作，此步骤需要MNs次CM运算，所以改进方法总的算法复杂度为20 M3＋（2P＋1）（2 MNb＋Na＋M）＋MVs.

令K＝2，P＝30，Na＝180，Nb＝30，Ns＝256，图11给出了各个方法对应的算法复杂度随阵元个数变化的情况.

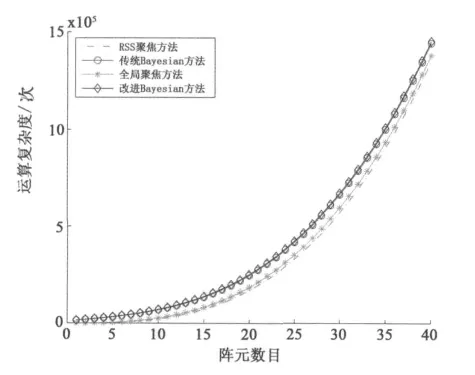
图11 各种方法运算复杂度的比较

从图11可以看出，改进的Bayesian方法和传统Bayesian方法拥有近乎相似的复杂度，相比于RSS聚焦方法和全局聚焦算法，在运算复杂度上只有微小的增长，而从之前的分析中可以看到，增长主要来自于式 （18）和（27）对应的计算.之前的实验结果已经表明：本文提出的改进方法，无论在和、差波束方向图、输出信干噪比以及单脉冲比曲线上，都具有更好的性能，算法的应用范围更广，应用条件更加宽松，那么微小的运算复杂度的增加也是可以接受的，该方法也更符合工程实际需要.

5 结 论

研究并提出了一种基于改进Bayesian聚焦的宽带自适应单脉冲测角算法.该算法在传统Bayesian算法的基础上，假设期望信号来波方向服从正态分布，干扰信号的来波方向服从均匀分布.仿真试验表明，改进方法一方面改进了文献［13］中的Bayesian聚焦方法和波束性能，另一方面也克服了原有方法不能直接被用来解决差波束问题的缺陷.新方法在几乎不增加运算复杂度的情况下，保证了单脉冲测角精度，对宽带自适应波束形成算法在实际工程中的应用更具有一定指导意义.

［1］任 超，吴嗣亮，王 菊.一种新的GPS接收机宽带干扰抑制方法［J］.电子与信息学报，2008，30（8）：1977-1981.REN Chao，WU Siliang，WANG Ju.A novel wideband interference cancellation method for GPS receiver［J］.Journal of Electronics and Information Technology，2008，30（8）：1977-1981.（in Chinese）

［2］MAYHAN J T，SIMONS A J，CUMMINGS W C.Wideband adaptive antenna nulling using tapped delay lines［J］.IEEE Transaction on Antennas and Propogation，1981，29（4）：923-936.

［3］DUAN H，NG B P，SEE C M S.Broadband beamforming using TDL-form IIR filters［J］.IEEE Transaction on Signal Process，2007，55（3）：990-1002.

［4］SEYDNEJAD S R，EBRAHIMI R.Broadband beamforming using Laguerre filters［J］.Signal Processing，2012，92（4）：1093-1100.

［5］杨益新，孙 超.任意结构阵列宽带恒定束宽波束形成新方法［J］.声学学报，2001，26（1）：55-58.YANG Yixin，SUN Chao.A new method of broadband constant beamwidth beamforming for arbitrary geometry arrays［J］.Acta Acustica，2001，26（1）：55-58.（in Chinese）

［6］鄢社锋，侯朝焕，马晓川，等.基于凸优化的时域宽带旁瓣控制自适应波束形成［J］.声学学报，2007年，32（1）：5-9.YAN Shefeng，HOU Chaohuan，MA Xiaochuan，et al.Convex optimization based adaptive broadband FIR beamforming with sidelobe control［J］.Acta Acustica，2007，32（1）：5-9.（in Chinese）

［7］杨花卫，黄建国.一种宽带恒定束宽自适应波束形成算法［J］.计算机仿真，2010，27（10）：339-342.YANG Huawei，HUANG Jianguo.A broadband constant beam width adaptive beamforming method［J］.Computer Simulation，2010，27（10）：339-342.（in Chinese）

［8］HUNG H S，MAO C Y.Robust coherent signal-subspace processing for direction-of-arrival estimation of wideband source［J］.IEEE Proceedings of Radar，Sonar and Navigation，1994，141（5）：256-263.

［9］HUNG H S，KAVEH M.Focusing matrices for coherent signal-subspace processing［J］.IEEE Transaction on ASSP，1988，36（8）：1272-1282.

［10］VALAEE S，KABAL P.Wideband array processing using a two-sided correlation transformation［J］.IEEE Transaction on Signal Process，1995，43（1）：160-172.

［11］侯云山，黄建国，金 勇.宽带信号方位估计的改进RSS方法［J］.系统工程与电子技术，2010，32（1）：1-5.HOU Yunshan，HUANG Jianguo，JIN Yong.Improved RSS method for the direction finding of wideband sources［J］.Systems Engineering and Electronics，2010，32（1）：55-58.（in Chinese）

［12］胡 航，王泽勋，刘会伟，等.相控阵的两级子阵加权方法研究［J］.电波科学学报，2009，24（6）：1038-1044.HU Hang，WANG Zexun，LIU Huiwei，et al.Twostage level weighting approach for phased array［J］.Chinese Journal of Radio Science，2009，24（6）：1038-1044.（in Chinese）

［13］胡 航，张 皓，宗成阁，等.子阵级自适应单脉冲的四通道主瓣干扰抑制［J］.电波科学学报，2009，24（5）：820-827.HU Hang，ZHANG Hao，ZONG Chengge，et al.Four channel mainlobe jamming suppression for adaptive monopulse at subarray level［J］.Chinese Journal of Radio Science，2009，24（5）：820-827.（in Chinese）

［14］胡 航，邓欣红.子阵级平面相控阵ADBF的旁瓣抑制方法［J］.电波科学学报，2008年，23（1）：201-206.HU Hang，DENG Xinhong.Sidelobe suppression method for ADBF at subarray level with planar array［J］.Chinese Journal of Radio Science，2008，23（1）：201-206.（in Chinese）

［15］BUCRIS Y，COHEN I，DORON M A.Bayesian focusing for coherent wideband beamforming［J］.IEEE Transaction on Audio，Speech and Language Processing，2012，20（4）：1282-1296.

［16］DORON M A，DORON E.Wavefield modeling and array processing：part I-spatial sampling［J］.IEEE Transaction on Signal Process，1994，42（10）：2549-2559.

［17］DORON M A，NEVET A.Robust wavefield interpolation for adaptive wideband beamforming［J］.IEEE Transaction on Signal Process，2008，80（10）：1579-1594.