强相干干扰下微弱信号波达方向估计

朱 伟 陈伯孝

（西安电子科技大学 雷达信号处理重点实验室，陕西 西安710071）

引 言

微弱信号的检测和参数估计广泛应用于雷达、通信、声纳和地震探测等领域.当存在强干扰源时，系统对微弱信号波达方向的估计精度会受到很大的影响.在阵列信号处理中通常的处理方法是使用超分辨算法对干扰和待检测信号同时处理，或者根据信号和干扰在空域、频域和时域的差异，在不同的域中进行分离、抑制，对待检测信号进行波达方向估计.前一种方法在一定程度上可以同时估计微弱信号和强干扰的波达方向，但是当干扰和信号相干或者位于一个波束宽度内时，干扰源与信号源的波达方向（Direction Of Arrival，DOA）估计效果较差，且估计信噪比门限较高；后一种方法主要有方向图零点综合、信号分离和数字波束形成技术等.

近年来，学者们提出了多种算法来进行强干扰环境下的弱信号DOA估计［1-14］.文献［1］提出了使用粒子群等优化算法进行阵列方向图综合，以降低副瓣电平并在干扰方向形成零点.文献［2］提出的松弛算法、文献［3］提出的洁净技术以及文献［4］提出的盲信号分离法，均是采用信号分离的方法使包含多个信号的阵列输出数据分离成几个数据块，而具体的某一个数据块只包含某一个信号的信息，从而分离出强干扰，达到干扰抑制的目的.数字自适应波束形成是通过控制波束的零点去对准干扰的来向，使用稳健的波束形成算法来形成零点，主要有对角加载算法［5］、最坏条件最优法［6］和迭代自适应最小方差法［7］等方法，但是当信号和干扰相干时，现有的大多数鲁棒波束形成算法性能都会严重下降.在以上算法基础上，文献［8］提出利用阵列环境中强干扰的先验知识构造阻塞矩阵来抑制干扰，从而实现对特定区域内低信噪比信号的DOA估计.文献［9］提出将接收的数据矢量划分成两个子矢量之后再重新构造新的数据矢量，在某些不确定集的约束下进行波束形成抑制相干干扰.文献［10］提出在已知干扰源个数和入射方向的前提下，将阵列划分成若干子阵，在子阵上进行波束形成以抗干扰，再对加权后的子阵进行微弱信号的DOA估计，该算法在信号与干扰不在一个波束内且互不相干时有良好性能.文献［11］提出一种自适应加权空间平滑解相干，然后利用线性约束最小方差准则得到子阵波束形成器最佳权矢量，再利用子阵间的相位关系对全阵进行波束形成的方法.文献［12］提出将阵列划分为两个虚拟子阵，分别对子阵进行波束形成来抑制干扰，然后利用子阵间的相位偏移来对弱信号进行DOA估计，该算法能显著消除同信道干扰的影响.文献［13］提出了使用迭代自适应波束形成来抑制干扰.文献［14］提出了一种迭代超分辨处理方法.以上算法在信号与干扰相干或者干扰位于主瓣内时性能较差.

针对空间干扰与待检测信号相干且空间间隔较小的情况，本文提出了一种强相干干扰下微弱信号DOA估计的新方法.该算法首先对强干扰源的个数和入射方向进行精确估计，再估计微弱信号源个数和参考入射方向，然后将阵列划分成两个虚拟子阵，使用波束形成来进行干扰抑制并提高待估计信号的信噪比，最后利用子阵间的相位偏移使用比相单脉冲进行DOA估计，并对子阵波束形成和DOA估计进行迭代运算以提高估计精度.

1 理论分析

1.1 信号模型

假设空间阵列是由M个阵元组成的均匀线阵，阵元间距为d，有P个相干微弱信号和K个相干强干扰以平面波形式入射到阵列上，P＋K＜M，入射方向分别为θSp（p＝1，…，P）和θJk（k＝1，…，K）.则阵列接收数据可表示为

式中：X（t）为M×1维阵列接收数据矢量；a（θ）＝［1，ej2πdsin（θ）/λ，…，ej2π（M-1）dsin（θ）/λ］T为θ 方 向 的 导 向矢量，其中λ为信号波长，上标T表示矩阵转置；sSp（t）和sJk（t）分别表示第p个信号和第k个干扰，信号和干扰相干，sSp（t）＝cSps（t），sJk（t）＝cJks（t），cSp和cJk为复常数；N（t）为M×1维噪声矢量，各阵元噪声统计独立，服从零均值、方差为σ2的复高斯分布.将式（1）右边两个求和项用矩阵表示为

式中：A（θ）＝［a（θS1），…，a（θSP），a（θJ1），…，a（θJK）］；

s（t）＝［cS1，…，cSP，cJ1，…，cJK］Ts（t）.

1.2 本文算法描述

本文算法的框图如图1所示，由干扰估计与目标粗估计、子阵波束形成和DOA估计三个模块组成.首先进行强干扰估计，在阵列上抑制干扰之后再得到目标的参考方向；将阵列划分成两个虚拟子阵，在子阵上进行波束形成来抑制干扰并提高待估计信号的信噪比；利用两个子阵的相位中心偏移来得到目标的精确DOA结果.

图1 本文算法框图

1.2.1 干扰估计与目标粗估计

对强干扰源的个数和入射方向进行精确估计.由于信号和干扰为相干信号，对数据协方差矩阵进行特征分解后，信号子空间退化为一维子空间，而噪声子空间的维数扩大为M-1维，无法通过特征值分解直接得到空间干扰的个数.通常情况下，干扰远强于待检测信号和噪声，相干信号源数目的估计方法［15］有平滑秩法、矩阵分解法和盖氏源方法等，相干信号源DOA估计的超分辨算法［15］有解相干多重信号分类算法、最大似然算法和Toeplitz近似法等.在高信噪比下，以上算法都能得到精确结果，在此不进行赘述，得到干扰的DOA估计为Jk（k＝1，…，K）.

在实际的诸如无线通信系统［16］等应用中，可以获得信号源的一些先验知识（如信号源个数和参考入射方向等）.在雷达、声纳等实际应用中，可以先在阵列上进行波束形成以抑制干扰［10］，然后再对加权后的阵列使用幅相估计 （Amplitude and Phase Estimate，APES）算法［17］得到微弱信号的个数和粗估计，将粗估计结果作为弱信号的参考入射方向，满足关系为

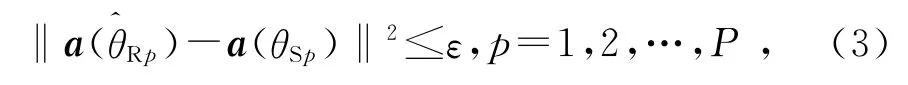
1.2.2 子阵波束形成

在子阵波束形成模块中，将M个阵元划分成两个相同大小的虚拟子阵.为了充分利用阵列孔径，通常有两种划分方法：最大重叠子阵法（Maximum O-verlapping Subarrays，MOSs）［18］和共轭子阵法（Conjugate Subarrays，CSs）［19］.

1）最大重叠子阵

最大重叠子阵包含两个M-1个阵元组成的虚拟子阵，其中阵列的前M-1个阵元组成子阵A，阵列的后M-1个阵元组成子阵B，如图2（a）所示.因此，子阵A和子阵B的接收数据分别为：

式中：

AA＿M（θ）＝［aA＿M（θS1），…，aA＿M（θSP），aA＿M（θJ1），…，

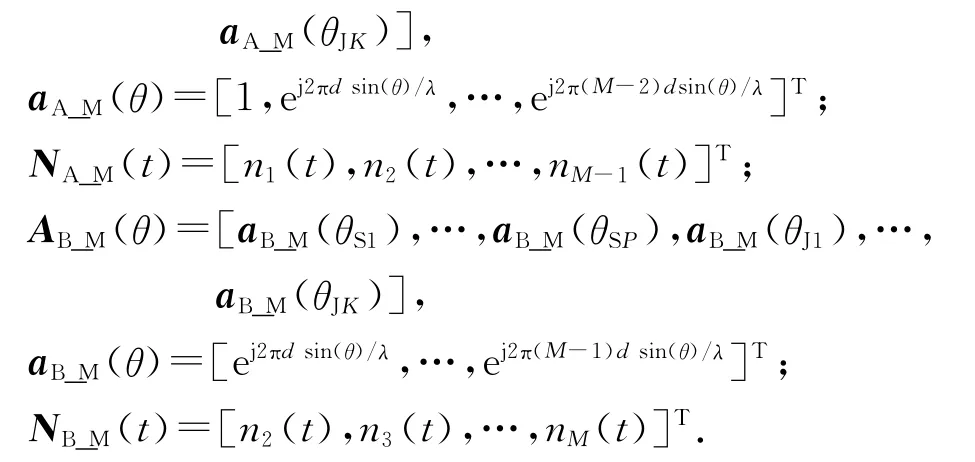
从式（4）和式（5）可以得出

式中，Φ＝diag ｛ej2πdsin（θS1）/λ， …，ej2πdsin（θSP）/λ，ej2πdsin（θJ1）/λ，…，ej2πdsin（θJK）/λ｝，diag表示对角阵.

2）共轭子阵

共轭子阵包含两个M个阵元组成的虚拟子阵，子阵A由一个虚拟阵元和阵列的前M-1个阵元组成，子阵B为当前阵列，如图2（b）所示.由于共轭子阵比最大重叠子阵多一个阵元，因此共轭子阵能获得更优的波束形成结果，但是共轭子阵的前提条件为信号包络为实包络，即s（t）＝s＊（t），上标＊表示共轭，文献［19-21］讨论了实际中信号满足实包络的条件.因此，子阵A和子阵B的接收数据分别为：

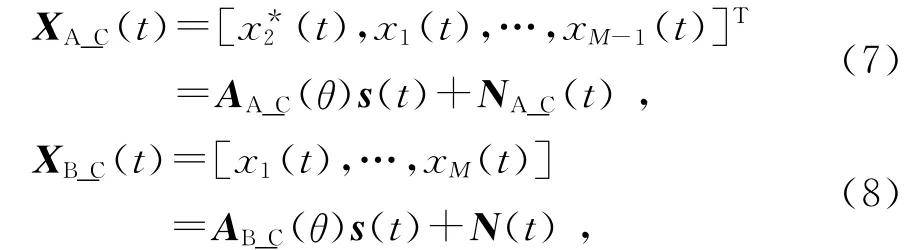
式中：AA＿C（θ）＝［aA＿C（θS1），…，aA＿C（θSP），aA＿C（θJ1），…，aA＿C（θJK）］，

从式（7）和式（8）可以得出

式中：Φ＝diag｛ej2πdsin（θS1）/λ，…，ej2πdsin（θSP）/λ，ej2πdsin（θJ1）/λ，…，ej2πdsin（θJ K）/λ｝.

从式（6）和式（9）可以看出：共轭子阵和最大重叠子阵具有一样的旋转不变性，旋转因子均为Φ，所不同的是最大重叠子阵的阵元数为M-1，而共轭子阵的阵元数为M，但共轭子阵中无孔径损失子阵的获得是基于信号包络为实包络，而最大重叠子阵则可运用复包络的情况.若无干扰且各信号源之间相互独立，在子阵A和子阵B间运用旋转不变子空间（Estimating Signal Parameters Viarotational Invariance Techniques，ESPRIT）算法，可得到各信号源的波达方向.

对于第p个待检测信号，进行子阵波束形成时需要在第p个待检测信号方向上得到最大的空间增益，而且抑制全部干扰，同时对待检测信号之外的其他信号也有一定的抑制，即子阵波束形成权值矢量wp需要满足以下线性方程组：

式中，上标H表示共轭转置；

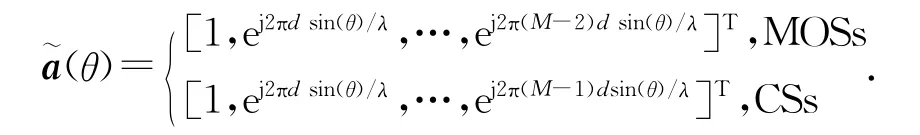
上述线性方程组无法直接计算，利用已估计的前p-1个信号的方向Sl（l＝1，…，p-1）、后P-p＋1个信号的参考方向Rl（l＝p，…，P）和已估计的干扰方向Jk（k＝1，…，K）得到以下线性方程组：

将方程组（11）写为矩阵形式有

式中：

于是，可得子阵波束形成权值wp为

分别对虚拟子阵A和虚拟子阵B进行波束形成，波束形成输出为

1.2.3 波达方向估计

通过波束形成后，干扰和除待检测信号之外的其他信号均得到了不同程度的抑制，两个子阵的相位中心间距为d，相应子阵A与子阵B间的相位中心偏移φp为

为了进一步提高信噪比，将yA（t）和yB（t）的L个快拍数据进行时域相参积累，得到SA和SB，SA和SB的幅度近似相等且相位差为φp，可以使用比相单脉冲［21］进行DOA估计，且有

利用相参积累结果SA和SB形成和信号S∑与差信号SΔ：

式中Im（）表示取虚部.

为了提高微弱信号的DOA估计精度，对子阵波束形成和DOA估计进行迭代运算，即用估计出的Sp代替式（13）中的Rp，并继续利用式（15）重新计算子阵波束形成权值wp，再次进行子阵波束形成和DOA估计.设置一定的终止条件，可以对待检测信号DOA进行较为准确的估计.

1.2.4 算法流程

综上所述，算法流程总结如下：

1）使用相干信源估计方法［15］来估计干扰源个数，并采用解相干超分辨算法［15］得到强干扰的DOA估计结果Jk（k＝1，…，K），然后在阵列上进行波束形成以抑制干扰［10］，再对加权后的阵列使用幅度相位估计（Amplitude and Phase Estimation，APES）算法［17］进行微弱信号的粗估计，得到参考方向Rp（p＝1，…，P）；

2）将阵列划分成两个虚拟子阵，信号包络为复包络时按照最大重叠子阵划分，信号包络为实包络时划分成共轭子阵；

3）对第p个信号进行步骤4至步骤6的过程；

4）通过式（12）至式（15）得到子阵波束形成的初始权值w（1）p，w（1）p的上标表示第几次迭代，然后利用式（16）分别对虚拟子阵A和虚拟子阵B进行波束形成；

5）对波束形成输出结果进行相参积累，按照式（20）生成和信号与差信号，并通过式（22）得到第p个信号的 DOA 初始估计值的上标表示第几次迭代；

为了进一步提高估计精度，可以将6）中得到的P个DOA估计值Sp（p＝1，…，P）作为参考方向Rp（p＝1，…，P），重复进行3）至6）的过程.

2 实验结果分析

为了分析本文算法的性能，将本文算法与文献［10］和文献［12］中的算法进行比较.考虑一个由10个全向阵元组成的均匀线阵，阵元间距d为半波长，3 dB波束宽度为10.15°.假设接收信号包络均为复包络，将阵列按最大重叠子阵的方式构造虚拟子阵.

实验1：多干扰下多目标的DOA估计性能比较

假设两个相干干扰方向为-50°和16°，干噪比均为80dB，三个相干信号分别从-11°、0.5°和12°方向入射，12°方向的信号与16°方向的干扰处在同一个波束宽度内，信噪比为0dB，信号的参考入射方向为-10°、0°和10°，信号与干扰相干，快拍数为100.迭代终止条件为δ＝0.001°.10 000次 Monte-Carlo实验DOA估计结果的统计直方图如图3所示.表1给出了三种算法的DOA估计均方根误差.

表1 三种算法DOA估计均方根误差

从以上统计直方图可以清晰地看出：文献［10］算法明显无法分辨多干扰下的多目标，尤其是无法分辨一个波束宽度内的目标和相干干扰；文献［12］算法能够检测多干扰下多目标，但是估计结果偏离真实角度较大，表明文献［10］和文献［12］算法对目标与相干干扰位于一个波束宽度内时不能进行DOA估计，而本文算法能很好地进行多相干干扰下多目标DOA估计，特别是在干扰与目标处于一个波束宽度内的情况下也能得到较好的结果.

实验2：多干扰下单目标的DOA估计性能随信噪比的变化

假设四个相干干扰方向为-50°、-30°、3°和40°，其中3°方向的干扰位于主瓣波束内，干噪比均为80dB，一个信号从-1°方向入射，信号的参考入射方向为1.5°，信号与干扰相干，快拍数为100，信噪比从-10dB变化至10dB.迭代终止条件为δ＝0.001°.1 000次 Monte-Carlo实验统计的DOA估计均方根误差如图4所示.均方根误差定义为

式中：P表示目标个数；N表示Monte-Carlo实验次数；Spn为第p个目标的第n次独立实验估计结果；θSp为第p个目标的真实值.

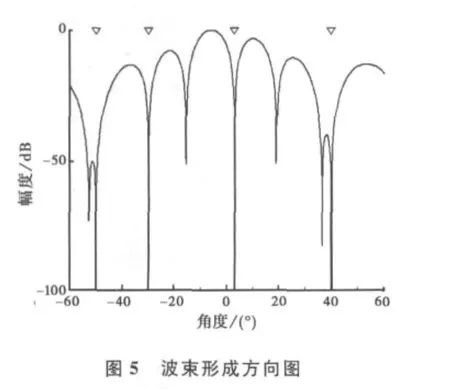
从图4结果曲线可看出：本文算法对多干扰下单目标的DOA估计性能优于文献［10］和文献［12］的算法，当信噪比大于8dB时，三种算法的估计性能趋于一致.图5给出了输入信噪比为10dB时子阵波束形成的方向图，从中可以看出干扰能得到较好的抑制.

实验3：多干扰下单目标的DOA估计性能随快拍数的变化

信号和干扰的仿真条件与实验2相同，信噪比为0dB，快拍数从10变化至1 000.迭代终止条件为δ＝0.001°.1 000次 Monte-Carlo实验统计的DOA估计均方根误差如图6所示.

图6 快拍数变化时的性能曲线

可见文献［10］、文献［12］和本文算法DOA估计精度随快拍数增加而提高，其中本文算法估计性能最优.

实验4：多干扰下单目标的DOA估计性能与导向矢量误差的关系

信号和干扰的仿真条件与实验2相同，信噪比为0dB，快拍数为100，信号的参考入射方向从-14.5°变化至1.5°.迭代终止条件为δ＝0.001°.1 000次Monte-Carlo实验统计的DOA估计均方根误差如图7所示.

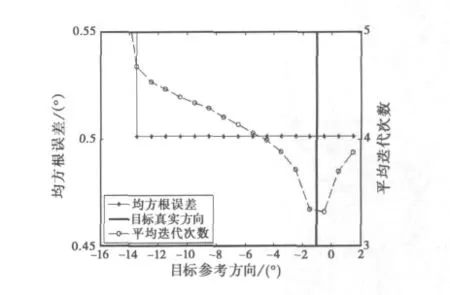
图7 DOA估计性能与目标参考方向的关系

从图7可看出：信号参考入射方向与真实入射方向相差大于一个波束时，性能急剧下降，算法无法收敛到目标的真实方向，但是参考入射方向与真实入射方向相差在一个波束宽度之内时，不影响目标的估计精度，但影响收敛速度，导向矢量误差越大，迭代次数越多，反之迭代次数越少.

实验5：空间邻近目标的估计性能

假设四个相干干扰方向为-50°、-30°、30°和50°，干噪比均为80dB，两相干信号从-2.5°方向和2.5°方向入射，两个信号处于半个波束宽度内，信号与干扰相干，信号的参考入射方向为-10°和10°，快拍数为100，考察不同信噪比下本文算法对两目标的估计性能，迭代终止条件为δ＝0.001°.由于两个信号空间间距很近，为了提高估计精度，在此可以将步骤6中得到的结果作为参考方向，再进行一次步骤3至步骤6的过程，得到更精确的估计结果.信噪比分别为0dB和10dB时，10 000次Monte-Carlo实验DOA估计结果的统计直方图如图8所示.图9给出了信噪比从-6dB变化至10dB，10 000次Monte-Carlo实验统计的DOA估计均方根误差.

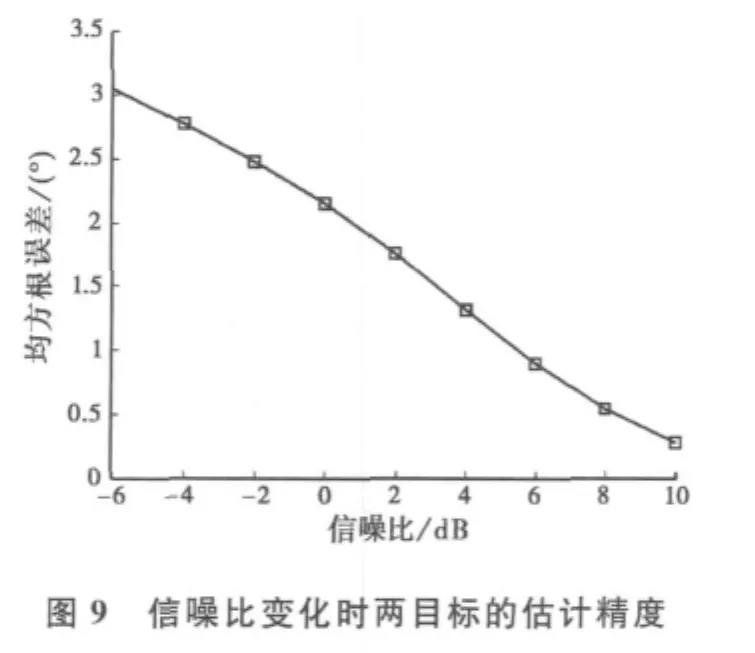
从图8和图9可以看出：信噪比越高，空间邻近目标的分辨性能越好，DOA估计精度随信噪比的增加显著提高.

3 结 论

提出一种均匀线阵下强相干干扰环境中进行微弱信号DOA估计的算法，利用子阵波束形成来抑制干扰并提高待估计信号的信噪比，然后使用比相单脉冲进行DOA估计，并且对子阵波束形成和DOA估计进行迭代运算以提高DOA估计精度.对于强相干干扰环境下系统对微弱信号的DOA估计问题，特别是当信号和干扰处在同一波束宽度内时，本文算法具有良好的性能.计算机仿真结果表明，相比文献［10］和文献［12］算法，本文算法具有更低的估计偏差和估计方差，性能更优.

［1］ISMAIL T H，HAMICI Z M.Array pattern synthesis using digital phase control by quantized particle swarm optimization［J］.IEEE Trans on Antennas and Propagation，2010，58（6）：2142-2145.

［2］LI J，STOICA P.Efficient mixed-spectrum estimation with applications to target feature extraction［J］.IEEE Trans.on Signal Processing，1996，44（2）：281-295.

［3］AKHDAR O，MOUHAMADOU M，CARSENAT D，et al.A new CLEAN algorithm for angle of arrival denoising［J］.IEEE Antennas and Wireless Propagation Letters，2009，36（4）：478-481.

［4］冶继民，张贤达，金海红.超定盲信号分离的半参数统计方法［J］.电波科学学报，2006，21（3）：331-336.YE Jimin，ZHANG Xianda，JIN Haihong.Semi-parametric statistical approach for overdetermined blind source separation［J］.Chinese Journal of Radio Science，2006，21（3）：331-336.（in Chinese）

［5］曾 操，廖桂生，杨志伟.一种加载量迭代搜索的稳健波束形成［J］.电波科学学报，2007，22（5）：779-784.ZENG Cao，LIAO Guisheng，YANG Zhiwei.Diagonal loading level estimation for robust beamforming［J］.Chinese Journal of Radio Science，2007，22（5）：779-784.（in Chinese）

［6］ELNASHAR A.Efficient implementation of robust adaptive beamforming based on worst-case performance optimisation［J］.IET Signal Processing，2008，2（4）：381-393.

［7］NAI S E，SER W，YU Z L，et al.Iterative robust minimum variance beamforming［J］.IEEE Trans on Signal Processing，2011，59（4）：1601-1611.

［8］陈 辉，苏海军.强干扰/信号背景下的DOA估计新方法［J］.电子学报，2006，34（3）：530-534.CHEN Hui，SU Haijun.A new approach to estimate DOA in presence of strong jamming/signal suppression［J］.Acta Electronica Sinica，2006，34（3）：530-534.（in Chinese）

［9］胡 航，景秀伟.基于近似理想方向图的子阵级超分辨测向方法［J］.电波科学学报，2007，22（4）：646-658.HU Hang，JING Xiuwei.Subarray level superresolution direction finding approaches based on approximate ideal patterns［J］.Chinese Journal of Radio Science，2007，22（4）：646-658.（in Chinese）

［10］柴立功，罗景青.一种强干扰条件下微弱信号DOA估计的新方法［J］.电子与信息学报，2005，27（10）：1517-1520.CHAI Ligong，LUO Jingqing.A novel algorithm for weak signals DOA estimation under intensive interferences［J］.Journal of Electronics ＆Information Technology，2005，27（10）：1517-1520.（in Chinese）

［11］周 围，张德民，吴 波，等.相干环境下LCMV自适应阵列抗干扰问题研究［J］.电子与信息学报，2007，29（7）：1604-1607.ZHOU Wei，ZHANG Demin，WU Bo，et al.Study on interference suppression for LCMV adaptive array in coherent environment［J］.Journal of Electronics ＆Information Technology，2007，29（7）：1604-1607.（in Chinese）

［12］WANG N Y，AGATHOKLIS P，ANTONIOU A.A new DOA estimation technique based on subarray beamforming［J］.IEEE Trans.on Signal Processing，2006，54（9）：3279-3289.

［13］DOISY Y，DERUAZ L，BEEN R.Interference suppression of subarray adaptive beamforming in presence of sensor dispersions［J］.IEEE Trans on Signal Processing，2010，58（8）：4195-4212.

［14］BLUNT S D，CHAN T，GERLACH K.Robust DOA estimation：the reiterative superresolution（RISR）algorithm［J］.IEEE Trans on Aerospace and Electronic Systems，2011，47（1）：332-346.

［15］王永良，陈 辉，彭应宁等.空间谱估计理论与算法［M］.北京：清华大学出版社，2009.

［16］OJANPERA T，PRASAD R.Wideband CDMA for third generation mobile communications［M］.Norwood：Artech House，1998.

［17］KENNY S R，MOE S，AHMED A K.High accuracy peak location and amplitude spectral estimation via tuning APES method［J］.Digital Signal Processing，2010，20：552-560.

［18］SOON V C，HUANG Y F.An analysis of ESPRIT under random sensor uncertainties［J］.IEEE Trans.on Signal Processing，1992，40（9）：2353-2358.

［19］TAYEM N，KWON H M.Conjugate ESPRIT （CSPRIT）［J］.IEEE Trans on Antennas and Propagation，2004，52（10）：2618-2624.

［20］DELMAS J P.Comments on “Conjugate ESPRIT（C-SPRIT）”［J］.IEEE Trans.on Antennas and Propagation，2007，55（2）：511.

［21］TAYEM N，KWON H M.Reply to comments on“Conjugate ESPRIT （C-SPRIT）”［J］.IEEE Trans.on Antennas and Propagation，2007，52（2）：512-513.

［22］朱 伟，陈伯孝，周 琦.两维数字阵列雷达的数字单脉冲测角方法［J］.系统工程与电子技术，2011，33（7）：1503-1509.ZHU Wei，CHEN Baixiao，ZHOU Qi.Angle measurement method with digital monopulse for 2-dimensional digital array radar［J］.Journal of Systems Engineering and Electronics，2011，33（7）：1503-1509.（in Chinese）