基于粒子群优化的偏斜α稳定分布参数估计

李静威 全厚德 崔佩璋

（军械工程学院光学与电子工程系，河北 石家庄050003）

引 言

短波（3～30MHz）是进行远距离无线通信的重要波段，而大气噪声是影响短波天波通信的重要因素之一.长期以来，该波段的信号处理研究往往假设环境噪声为高斯噪声，但在实际应用和研究中都发现，由于大气放电，环境噪声并不符合高斯噪声的统计特性，而具有较强的冲击特性.特别在15MHz以下，大气噪声冲击特性非常明显［1-5］，给短波通信造成了很大影响.冲击噪声的统计特性具有非高斯和重尾的特性，而这些特性恰恰符合α稳定（αS）分布［6］.环境噪声特性研究是一项基础性工作，因此其参数估计受到研究者的广泛关注.

国内外学者对αS分布模型的参数估计提出了多种方法，主要有特征函数法（CFM）［7-8］、分位数法（QM）［9-10］、极大似然估计法（MLE）［11-13］、极大值估计法（EVM）［14-15］、矩估计法（MM）［15-16］、联合估计（JE）［17］以及贝叶斯参数估计（BE）［18-19］等.其中，CFM、QM、MLE是通用的参数估计方法，但是αS分布独有的非线性、无限方差、无闭式的概率密度函数（PDF）等特性给估计带来了很多困难.EVM是基于αS分布重尾性的估计方法，但是EVM需要查表确定样本的分组大小.JE是对以上几种方法的综合应用.在很多情况下，可采用整数阶矩进行统计参数估计，但是αS分布的二阶及高阶矩是无限的，因此并不适用.分数低阶矩（FLOM）的提出为αS分布的参数估计提供了特有的方法.以上方法除BE外待估参数都必须按照特定顺序逐一估出，无法同时得到.然而，BE虽能同时进行多参数估计，但需提前给出3种先验分布中的6个参数，参数设置的复杂性及随机性对后续的估计影响较大.

粒子群优化（PSO）［20］算法是 Kennedy和Eberhart于1995年提出的一种随机全局优化算法.该算法具有在较高维空间发现全局最优解的能力，可解决大量非线性、不可微和多峰值等复杂优化问题，实现简单，收敛速度较快，稳定性好［21］.本文针对αS分布的非线性、无限方差及无闭式PDF的实际选取PSO算法，结合αS分布的FLOM 特性，提出了PSO-FLOM方法，实现了αS分布多个参数的同时估计.蒙特卡罗（MC）仿真实验证明了本方法的有效性和准确性.

1 α稳定分布

α稳定分布是目前惟一符合广义中心极限定理的分布类型，即无限多个可能方差无限大的独立同分布的随机变量和的极限分布是αS分布.因其没有闭式PDF，只能由特征函数进行表征.目前，αS分布具有三种不同的参数系表征方法，分别称为S标准参数系、S1参数系和S2参数系［22-23］.S参数系在信号处理中使用普遍，也是文献中最为常用的［24］，因此仅讨论S参数系下的参数估计.

定义1 称随机变量X具有一个稳定分布，如果存在四个参数 （α，β，σ，μ），其中0＜α≤2，-1≤β≤1，0＜σ，μ为实数，其特征函数具有式（1）形式：

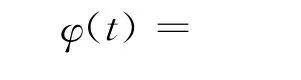
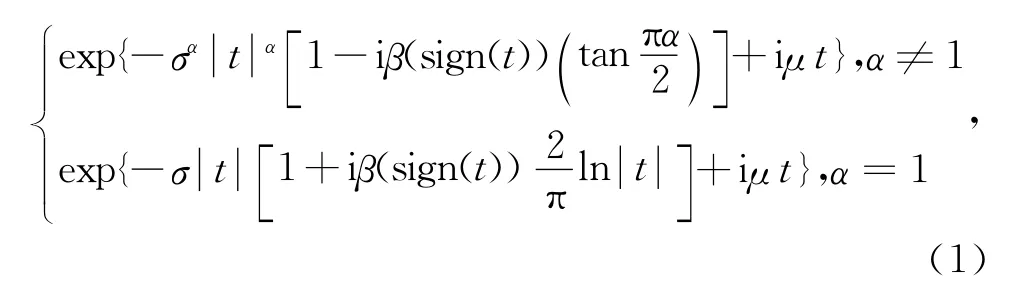
α称为特征指数，决定该分布脉冲特性的程度.α值越小，所对应分布的拖尾越厚；相反，随着α值变大，所对应的拖尾变薄，且脉冲特性减弱.β称为对称参数，用于确定分布的偏斜程度.β＝0对应于对称分布，称为对称α稳定（SαS）分布；-1≤β＜0对应左偏斜分布；0＜β≤1对应右偏斜分布.σ为尺度参数，又称分散系数，它是关于样本相对于均值的分散程度的度量.μ为位置参数，用于确定PDF的位置.

特别的，α＝2时，该分布为高斯分布；α＝1，β＝0时为柯西分布；α＝1/2，β＝-1时为泊松分布.除这三种特殊情况外，αS分布的PDF没有封闭的表达式.四个指数的灵活取值使该分布具有广泛的适应性.

2 Kuru-FLOM估计

若随机变量X满足

令γ＝σα，则X的分布亦可表示为

对于α≠1，偏斜αS分布的绝对FLOM理论值为

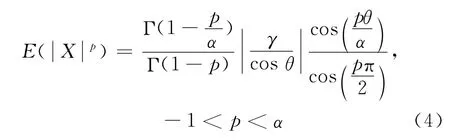
其符号FLOM理论值为

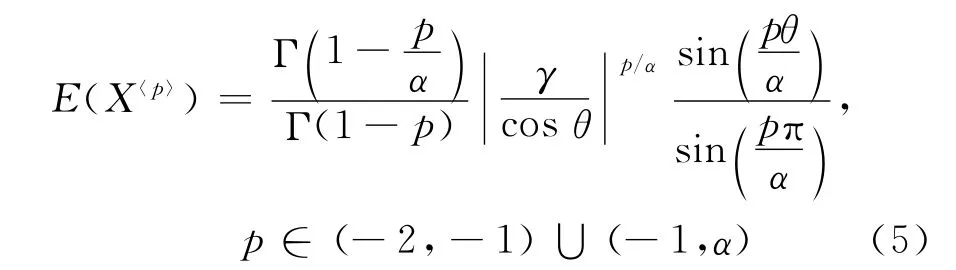
一个具有N个样本点的随机变量X，其绝对FLOM和符号FLOM的估计为

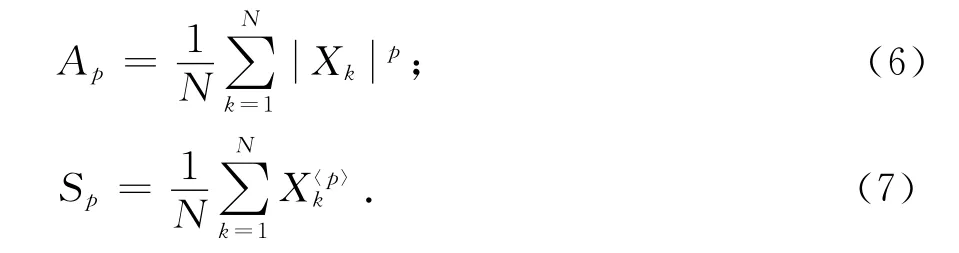
通过FLOM的乘积与比值，利用伽马函数式（8）的性质，可得到一些简单的α、β和γ的闭合表达式.

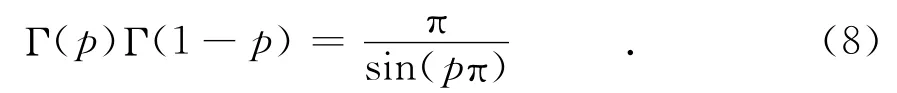
1）α估计式

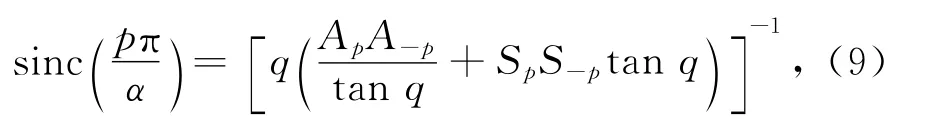
2）α估计出来后，利用估值α＾和β的估计式（10）进行β的估计.

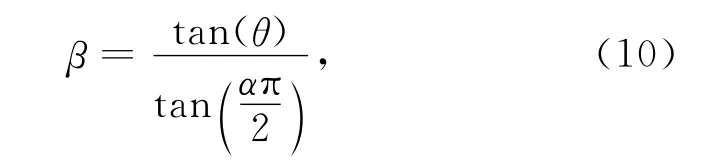
式中θ可由Sp/Ap、ApS-p、ApA-p、SpS-p等得到.但后两种无法确定β的符号.

3）估计出α和θ后，利用下式估计γ为

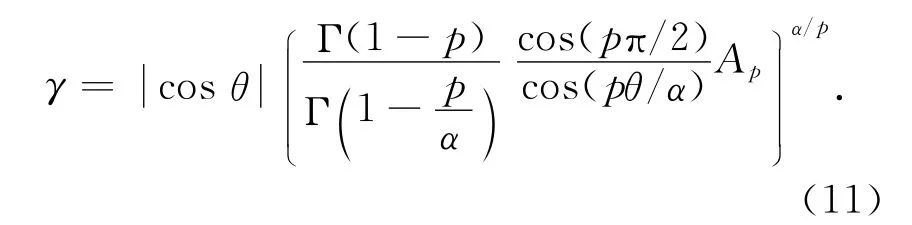
并根据γ＝σα，得到σ的估值.

3 PSO-FLOM估计

3.1 PSO算法原理

PSO算法首先初始化一群随机粒子（随机解），每个粒子具有位置和速度两个特征.粒子位置坐标对应的目标函数值为该粒子的适应度，算法通过适应度来衡量粒子位置的优劣.假设D维搜索空间中第i个粒子的位置和速度分别为Xi＝（xi1xi2… xiD）、Vi＝（vi1vi2… viD），在每次迭代中，粒子通过跟踪两个最优解来更新自己，第一个是该粒子本身最优解，即个体极值，Pi＝（pi1pi2… piD）；另一个是整个种群目前找到的最优解，即全局最优解Pg.找到两个最优值后，第i个粒子的第j维向量根据下面两式来更新自己的速度和位置.

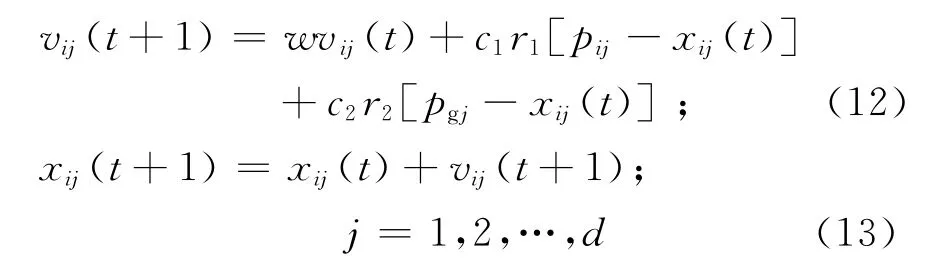
式中：w为惯性权因子，它使粒子保持运动的惯性，使其有能力探索新的区域；c1和c2为正的学习因子，分别调节全局最好粒子和个体最好粒子飞行的最大步长；r1和r2为0到1之间均匀分布的随机数.

更新过程中，粒子每维的坐标限制在 ［xmin，xmax］.根据αS分布参数定义域确定取值范围，提出位置映射进行限制.以α∈（0，2］为例，当粒子该维的更新值为α′，α的取值为

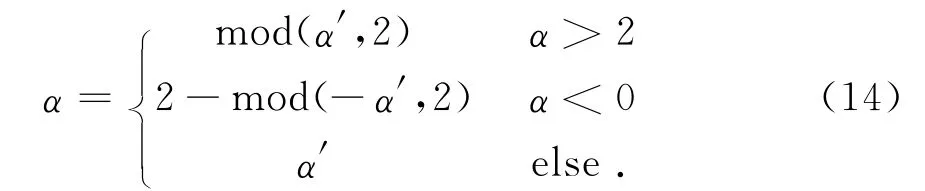
按照同样方法，根据β和σ值域分别进行相应的映射，保证迭代值落在各自定义域中.

3.2 目标函数确定

3.2.1 目标函数选取

根据FLOM理论式和估计式，选用绝对FLOM.偏斜αS分布模型参数估计就是使式（15）最小化的参数取值，即

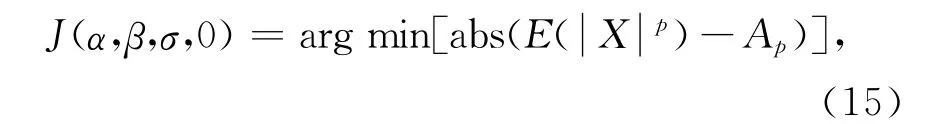
式中p为FLOM的阶次.

3.2.2 阶数p的选择

p≥α时，FLOM值为无穷，因此需p＜α.FLOM的协方差在p＝α/2时也是无限的［15］.根据式（15），分别计算了在β＝0.5、σ＝1、μ＝0、α＝［0.5，0.9，1.3，1.7］四种情况下，p＜α时，目标函数随p值变化的情况.目标函数值为1时，p值分别为 ［0.17，0.32，0.50，0.74］，分 别 对 应 于 α 值 的0.34、0.36、0.38和0.44倍.以α＝1.7为例，图1给出了两者的关系曲线.从图1可以看出：α/2＜p＜α时，误差较为平稳，基本保持在1值附近；p＝α/2附近时误差急剧增大；p＜α/2时误差具有较明显下降趋势，且越接近0值下降趋势越强.因此，进行估计时，p值至少应小于α/2.依据这一原则，p值的大小并不会影响估计算法的实质.

3.2.3 β符号的确定

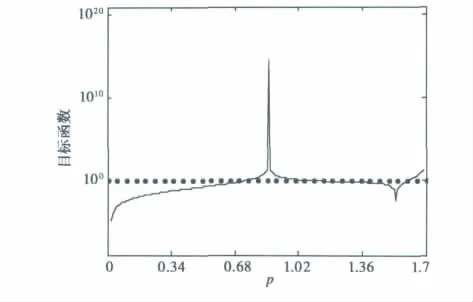
图1 目标函数随p值变化曲线

借鉴简便的样本分位数法，首先确定β的符号以缩小β值的搜索范围，提高搜索效率.若Xmd表示随机序列的中位数，Xmin表示序列中的最小值，Xmax表示序列中的最大值，则Xmin和Xmax亦分别代表了分布左右两端的分位数.

综上分析，PSO-FLOM流程如图2所示.

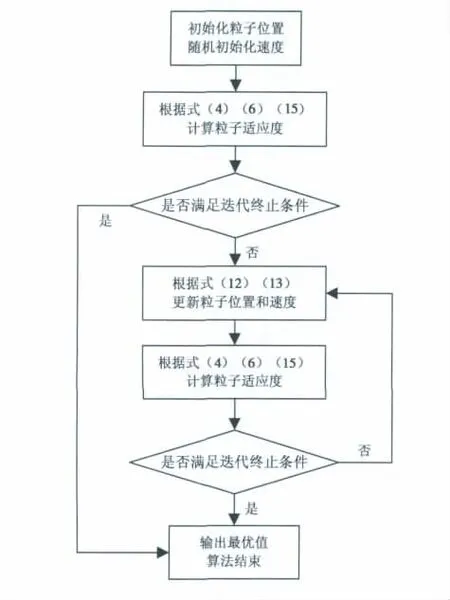
图2 PSO-FLOM流程图

表1 β的符号判断

4 仿真实验与分析

根据αS分布参数特点，结合PSO算法的经验和准则，PSO-FLOM参数设置为：粒子群规模30，维数3，α、β、σ值域分别为（0，2］、［0，1］、［0，2］，粒子初始速度为0.5＊rand，学习因子c1、c1分别设为2.8和1.3，迭代次数为500.不失一般性，FLOM阶次p＝0.3.PSO算法本质是一种随机算法，即使用同样的参数，每次求解的结果也可能不同，故进行200次MC仿真后取其均值.

表2给出了Kuru-FLOM和PSO-FLOM两种方法的估计结果，同时给出了估计值误差相对真值的误差比（ER）.实验1显示，PSO-FLOM的估计参数精度分别提高了2.4%、4.2%、2.2%；实验2显示，PSO-FLOM 的估计精度分别提高了2.8%、4.4%、2.4%；实验3显示，PSO-FLOM 的估计精度分别提高了-0.8%、5.6%、0.2%.实验1和实验2在估计精度上都有了明显的提高，而实验3除α估计精度略有下降外，其余2个参数估计精度也有所提高.其原因为实验3的α真值有所降低，根据FLOM阶数p值的选取规律，要达到与实验1、2相应的估计精度，p值需适当减小.总之，PSO-FOLM方法对比Kuru-FLOM方法的估计精度有所提高或相当.在多参数估计方式上，前者能同时给出多个参数估值，而后者必须依次给出参数估值.

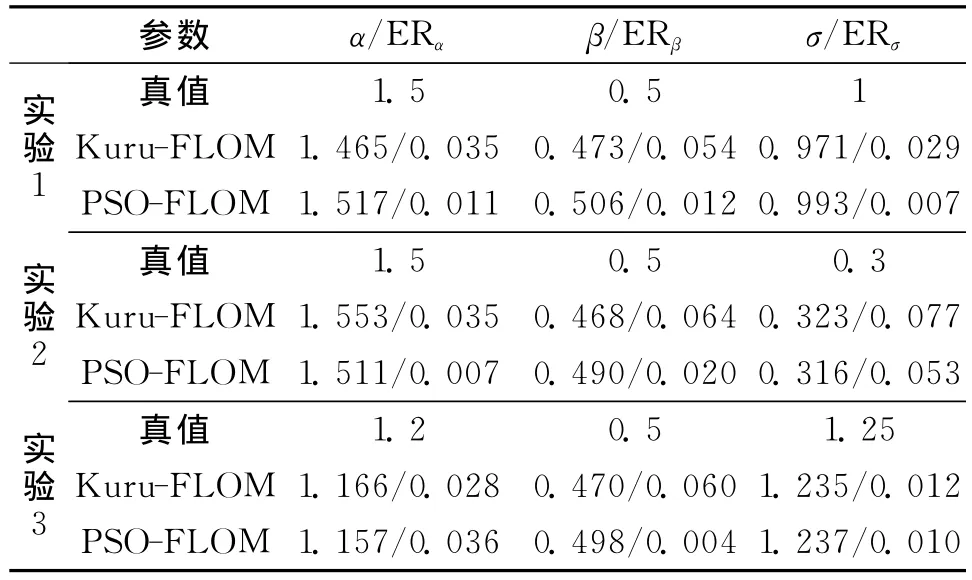
表2 试验结果对比

根据仿真实验估计结果，图3分别给出3个实验估值与真值情况下得到的αS分布随机序列的PDF曲线.可以看出：实验1和实验2中由PSOFLOM方法的估计结果产生的PDF曲线更加接近真值曲线，说明其是有效的，且较为精确；实验3中两种估计方法所得的PDF曲线相当.因为αS分布由4个参数综合决定，每个参数存在偏差都会对估计曲线产生影响，即使估计精度较高，估值曲线与真值曲线也并不会完全重合，在α值较小时，综合影响的程度更加明显.

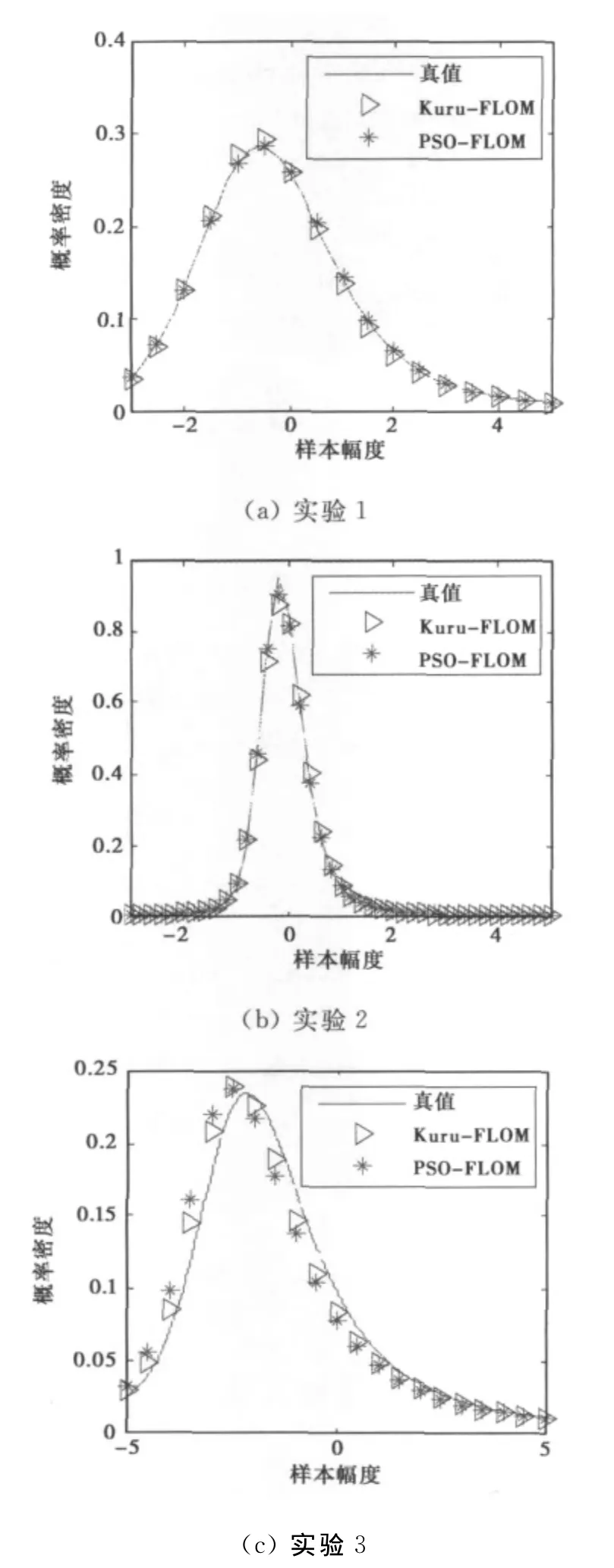
图3 仿真实验结果PDF曲线对比

5 结 论

提出了基于粒子群优化的偏斜α稳定分布参数估计，并在对称参数β符号确定和FLOM阶次p选取上给出了相应分析，进而确定了算法的目标函数和PSO-FLOM估计方法的流程，最后通过仿真实验验证了该方法的有效性.仿真实验显示该方法PSO参数设置简单，克服了Kuru-FLOM估计方法必须逐步给出α、β、σ估计值的不足，能够同时得到3个参数的估计值，估计精度有所提高或与之相当.虽然偏斜αS分布的FLOM参数估计研究还限于位置参数μ＝0的情况，但无疑PSO-FLOM给偏斜α稳定分布参数估计提供了一种简单有效的新选择.

［1］KRAMER J D R，WILLIAMS R T.High frequency atmospheric noise mitigation［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing.Adelaide，April 19-22，1994：101-106.

［2］LAUBER W R，BERTRAND J M.HF atmospheric noise levels in the Canadian arctic［J］.IEEE Trans on Electromagnetic Compatiblity，1994，36（2）：104-109.

［3］SHINDE M P，GUPTA S N.A model of HF impulsive atmospheric noise［J］.IEEE Trans on Electromagnetic Compatiblity，1974，16（2）：71-75.

［4］AGARWALA R A.Frequency characteristics of atmopheric noise［J］.IEEE Trans on Electromagnetic Compatiblity，1983，25（2）：119-120.

［5］黄德耀，王聚杰，杨维富，等.福建地区大气无线电噪声的某些特征［J］.电波科学学报，2002，17（6）：650-655.HUANG Deyao，WANG Jujie，YANG Weifu，et al..Atmospheric radio noise characteristics of Fujian regions［J］.Chinese Journal of Radio Science，2002，17（6）：650-655.（in Chinese）

［6］SHAO M，NIKIAS C L.Signal processing with fractional lower order moments：stable processes and their application［J］.Proceedings of the IEEE，1993，81（7）：986-1010.

［7］KOUTROUVELIS I A.Regression-type estimation of the parameters of stable laws［J］.Journal of the American Statistical Associstion，1980，75（4）：918-928.

［8］WILLIAMS S K.Characteristic function based estimation of stable distribution parameters［M］.Berlin：Birkhauser，1998.

［9］ROLL F F E.Parameter estimations for symmetric stable distribution［J］.Journal of the American Statistical Associstion，1971，66（2）：331-338.

［10］MCCULLOCHJ H.Simple consistent estimators of stable distributions［J］.Communications in Statistics-Simulation and Computation，1986，15 （4）：1109-1136.

［11］MITTNICS，RAVHEV S T，DOGANOGLU T.Maximum likelihood estimation of stable paretian models［J］.Mathematical and Computer Modelling，1999，29（1）：275-293.

［12］BODENSCHATZ J S，NIKIAS C L.Maximum-likelihood symmetric alpha-stable parameter estimation［J］.IEEE Trans on Signal Processing，1999，47（5）：1382-1384.

［13］NOLAN J P.Maximum likelihood estimation and diagnostics for stable distributions［D］.Washington：American Univeristy，2002.

［14］TSIHRINTZIS G A，NIKIAS C L.Fast estimation of the parameters of alpha-stable impulsive interference［J］.IEEE Trans on Signal Processing，1996，44（6）：1492-1503.

［15］KURUOGLU E E.Dendity parameter estimation of skewedα-stable distributions［J］.IEEE Trans on Signal Processing，2001，49（10）：2192-2201.

［16］MA X Y，NIKIAS C L.Parameter estimation and blind channel identification in impulsive signal environments［J］.IEEE Trans on Signal Processing，1995，43（12）：2884-2897.

［17］LI X J，JIN L W，LI X T.Joint parametrs estimation for general alpha stable random noise［C］// 2008 Congress on Image and Signal Processing.Sanya，May 27-30，2008：465-469.

［18］LOMBARDI M J.Bayesian inference forα-stable distributiongs：A random walk MCMC approach［J］.Computational Statistics ＆ Data Analysis，2007，51（5）：2688-2700.

［19］郝燕玲，单志明，沈 锋.基于自适应Metropolis算法的α稳定分布参数估计［J］.系统工程与电子技术，2012，34（2）：236-242.HAO Yanling，SHAN Zhiming，SHEN Feng.Parameter estimation ofα-stable distributions based on adaptive Metropolis algorithm［J］.Systems Engineering and Electronics，2012，34（2）：236-242.

［20］KENNEDY J，EBERHART R.Particle swarm optimization［C］//Proc of the IEEE International Conference on Neural Networks.Perth，27Nov 1995-01 Dec 1995：1942-1948.

［21］曹运华，吴振森，齐利华，等.粒子群算法在BRDF模型参数优化中的应用［J］.电波科学学报，2008，23（4）：765-768.CAO Yunhua，WU Zhensen，QI Lihua，et al..Application of particle swarm optimization algorithms to parameter optimization of BRDF model［J］.2008，23（4）：765-768.（in Chinese）

［22］NOLAN J P.Parameterizations and modes of stable distributions［J］.Statistics ＆ Probability Letter，1998，38（2）：187-195.

［23］RAFAL W.On the chambers-mallows-stuck method for simulating skewed stable random vairables［J］.Statistics ＆ Probability Letter，1996，28（2）：165-171.

［24］李旭涛，朱光喜，王首勇，等.Alpha稳定分布的参数表征及仿真［J］.信号处理，2007，23（6）：814-817.LI Xutao，ZHU Guangxi，WANG Shouyong，et al..Parameterizations and simulation of alpha stable distribution［J］.Signal Processing，2007，23（6）：814-817.（in Chinese）