裂缝宽度对探地雷达波场影响的对比分析

郭士礼 朱培民 施兴华 李修忠

（1.中国地质大学（武汉），湖北 武汉430074；2.中国电波传播研究所，山东 青岛266107；3.黄淮学院，河南 驻马店463000）

引 言

裂缝是工程构筑物的常见病害，一般遵循从无到有、从窄到宽的发育规律，若能尽早通过检测发现裂缝并及时采取有效治理措施是非常关键的.

许多学者在裂缝的波场特征方面做了大量的研究.刘江平等［1-3］从射线理论的角度阐述了垂直裂缝的反射波同相轴呈现似“八”字形特征，提供了判断垂直裂缝是否存在的依据.李修忠［4-5］等人详细分析了裂缝的波场特征及其探地雷达检测方法，在识别裂缝，判断裂缝的位置、深度及走向等方面具有重要意义.李成香［6］等阐述了探地雷达在宜黄高速公路路面裂缝检测中的应用并对公路路基变形程度提出四种划分标准.杨成林［7］等人利用探地雷达调查滑坡裂缝的位置、深度及走向，为后期滑坡治理提供依据.王国群［8］总结了裂缝的探地雷达图像基本特征，分析了不同成因地裂缝的探测机理和雷达图像特征.以上研究主要是依据裂缝的波场特征判定裂缝是否存在，并识别裂缝的位置、深度及走向等信息.文章在前人研究的基础上，通过理论分析、数值模拟和物理模拟实验研究了当垂直裂缝的宽度变化时，其波场的动力学特征变化规律，尤其对于微裂缝，由于其宽度的变化量在水平方向上非常微小，相应的其波场特征的变化则主要表现在动力学方面，文章着重分析其波场的振幅与宽度变化之间的关系.

1 理论分析

时域探地雷达一般采用类似雷克子波的雷达脉冲［9］，我们采用如图1（a）所示的雷克子波，该子波的主瓣半周期为6（对应半波长为6个长度单位），振幅最大值为5.3.假定有一极窄的无限长垂直裂缝，其宽度为一个长度单位，此时裂缝底端不会对顶端的散射产生影响，相当于一个点元.当雷达仪器位于该垂直裂缝正上方时，其自激自收得到的裂缝顶部散射波也如图1（a）所示的一个雷达子波.

把该裂缝同时向两侧加宽，每次向两侧各增加一个长度单位，则生成宽度依次为包含1、3、5、7…、41个长度单位的21个不同宽度的裂缝.以第21个单位长度裂缝为中心，计算宽度分别为1、3、…、41个长度单位的裂缝的雷达波响应曲线.以裂缝宽度为3个单位长度为例，位于天线正下方的单位长度裂缝产生的雷克子波最先到达天线接收点，而左边和右边单位长度裂缝产生的雷克子波则滞后一个单位时间，根据电磁波的叠加原理，三个单位长度的裂缝响应波形为三个雷克子波的叠加，其最大振幅值出现在三个雷克子波振幅相干加强的最大点.以此类推，得到其他不同宽度裂缝的雷达散射波波形图，如图1（b）所示（从左至右依次为1、3、…，41个长度单位的裂缝散射波波形图，波形图上的数字代表裂缝宽度）.

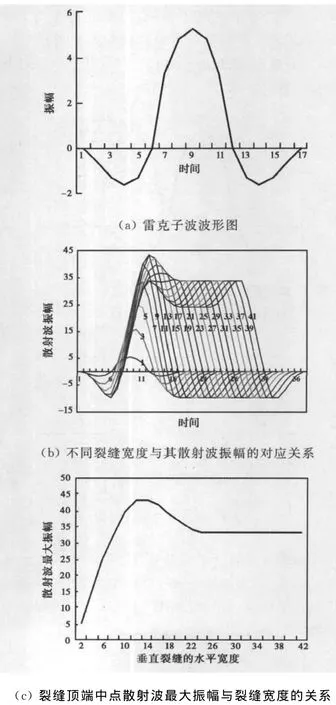
图1 裂缝宽度与其散射波最大振幅的对应关系

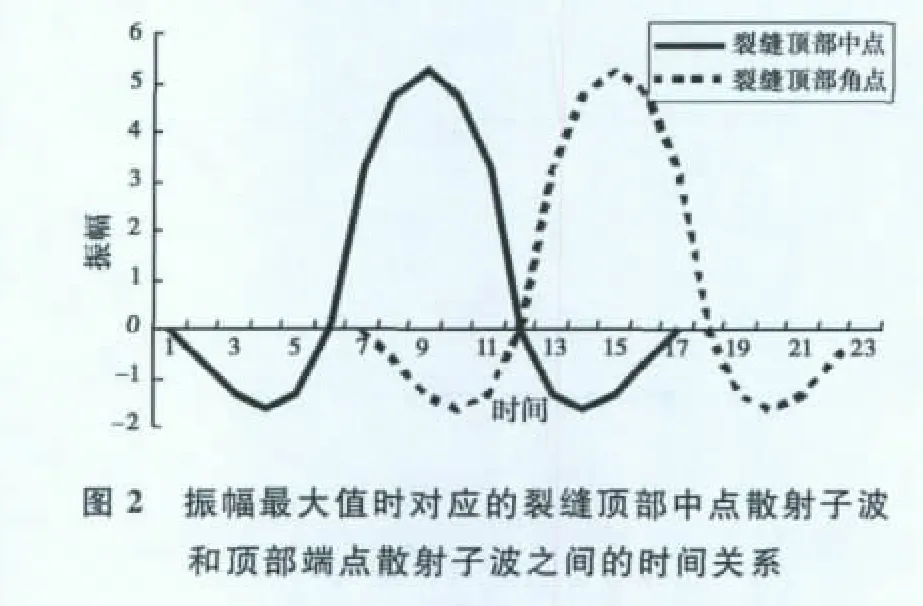
对不同宽度裂缝顶端中点散射波提取振幅最大值并绘制振幅随裂缝宽度变化的关系曲线，如图1（c）所示.从该曲线可以看出，当裂缝的宽度小于一个子波的视波长时，裂缝顶部中点散射波振幅随裂缝宽度的变大而增强，特别是当裂缝宽度小于半个视波长时，裂缝顶部中点散射波振幅与裂缝宽度成近似直线关系；当裂缝宽度约等于雷克子波的一个视波长（12）时，振幅达到极大值，超过一个视波长后首先衰减，然后趋于一个稳定值.将裂缝中心点的散射子波与振幅达到最大值时裂缝顶部端点的一个子波抽出绘于图2，可见，两个子波的主瓣刚好处于分离点上.当裂缝宽度小于该值时，位于这两个子波之间的所有散射子波均相干加强；当裂缝宽度大于该值时，超出该宽度的散射子波会使中心点的散射波削减；当裂缝宽度超过一定值后，对裂缝中点散射波的振幅不再有影响.

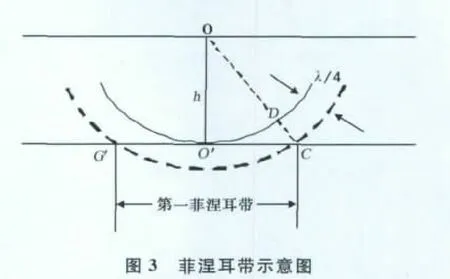
当综合考虑雷达子波的波长λ与裂缝顶端的埋深h的影响时，裂缝宽度等于第一菲涅尔带直径时，其散射波振幅强度最大.如图3所示，第一菲涅耳带直径指CC′界面段，其值为：

当裂缝宽度小于等于该值时，位于该直径之内的所有散射子波均发生相长性干涉，振幅增强；当裂缝宽度大于该值时，超出该直径的散射子波会使中心点的散射波削减；当裂缝宽度超过一定值后，对裂缝中点散射波的振幅不再有影响.

2 数值模拟

数值模拟不同宽度垂直裂缝的雷达波响应特征.模型宽2.5m，高0.65m，垂直裂缝垂向长0.2m，裂缝顶深0.2m，宽度分别为0.5mm、1.5 mm、7.5mm、15mm、30mm、40mm、60mm、70 mm、125mm、225mm、250mm、270mm、500mm.采用二维时间域有限差分方法，UPML吸收边界条件，激励源采用中心频率为900MHz的雷克子波，母体介质相对介电常数为4，裂缝的相对介电常数为1，此时第一菲涅耳带为0.27m.取等距网格步长0.5mm，基于图形处理器并行计算方法［10］进行数值模拟，合成的自激自收部分扫描图如图4（a）所示.图4（b）给出了裂缝顶部中点处散射波最大振幅随宽度变化的关系曲线.

从图4（a）数值模拟剖面图中可以看出，探地雷达对单个裂缝的探测能力远远小于第一菲涅尔带半径，且垂直裂缝表现为对应于裂缝顶、底端的两条双曲线波组，其中，顶端的双曲线波组的能量较强，而裂缝底端对应的双曲线波组能量较弱，且两者相位相反.这是因为在与垂直裂缝正交的二维平面内，垂直裂缝的断面可简化为一条线段，将该线段细分为无穷多个“小段”后，则每个“小段”可等效为一个异常点元，每个异常点元可形成一条散射双曲线波组，所有这些异常点形成的散射双曲线波组经过叠加，除裂缝顶、底两端点外，其他对应于中间部分的波组正、负相位将相互抵消，叠加后能量趋于零［5］，并可据此判断裂缝的顶、底端位置，但无法从雷达剖面图上识别裂缝宽度，只有当裂缝宽度超过第一菲涅尔带直径时，才能从雷达剖面图直接识别裂缝两侧的边缘位置.

从图4（b）可以看出，当裂缝宽度小于第一菲涅尔带直径时，裂缝顶部中点散射波振幅随裂缝宽度的变大而增强，特别是当裂缝宽度小于第一菲涅尔带半径时，裂缝顶部中点散射波振幅与裂缝宽度成近似直线关系；当垂直裂缝宽度约等于第一菲涅尔带直径（0.27m）时，裂缝顶部中点处散射波最大振幅达到最大值，超过该宽度后，振幅开始有所衰减，然后趋于一个恒定值，说明雷达波场动力学特征对目标体横向上的尺度变化有一个敏感范围，其大小约等于对应深度的第一菲涅耳带的直径，超出该范围后首先衰减，然后趋于一个稳定值，此时从雷达剖面图上可以直接识别裂缝两侧端点位置，从而确定裂缝宽度.

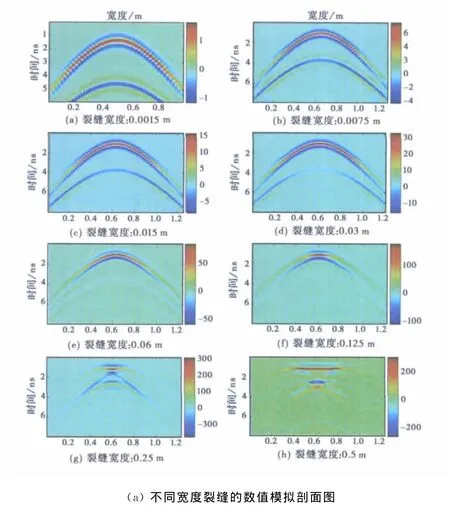
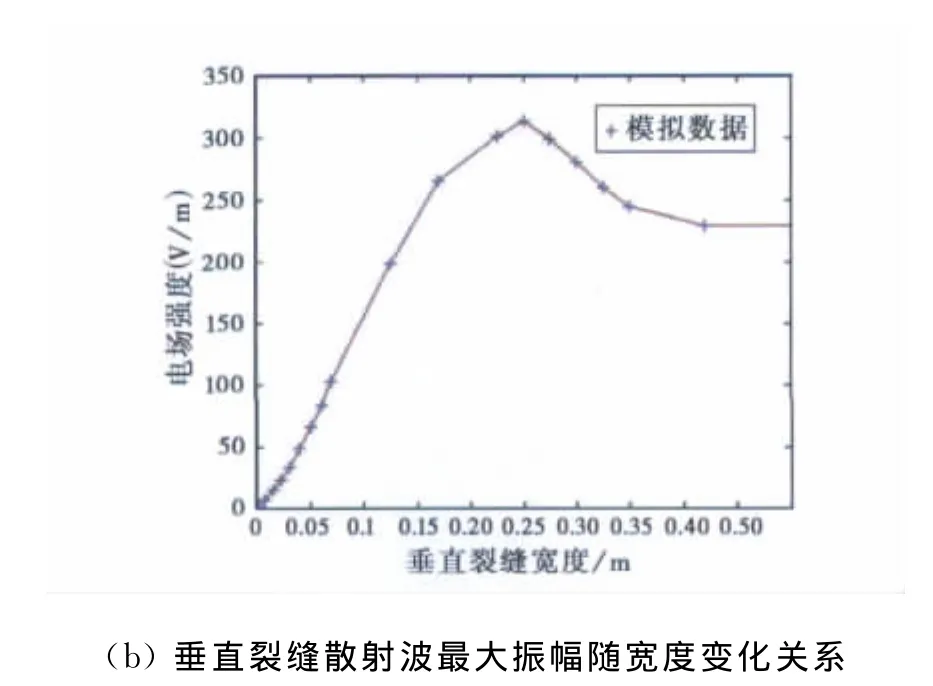
图4 不同宽度裂缝的数值模拟剖面及其散射波最大振幅随宽度变化关系曲线

而实际工程中的裂缝一般远小于第一菲涅尔带半径.从图4（b）可以看出，当裂缝宽度约小于第一菲涅尔带半径时，其顶端散射波的振幅与裂缝的宽度之间呈明显的近似直线关系，而且裂缝越窄，直线关系越明显，这种近似直线关系为我们定量化测量裂缝宽度提供了理论依据.

设散射波电场强度峰值为Ez，裂缝宽度为x，则

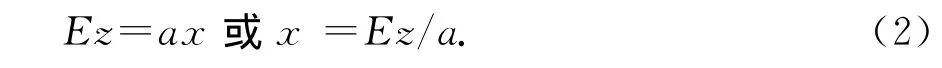
式中：a为比例系数，单位为mv/mm2；Ez为裂缝顶端散射波电场强度峰值，单位为mv/mm；x为裂缝宽度，单位为mm.采用最小二乘法对模拟结果（见表1）进行回归分析求得比例系数a≈1 200（v/m2），则垂直裂缝顶部中点处散射波最大振幅Ez与裂缝宽度x之间的关系可近似表示为下面的一条过原点的直线

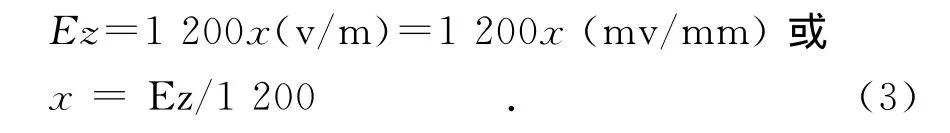
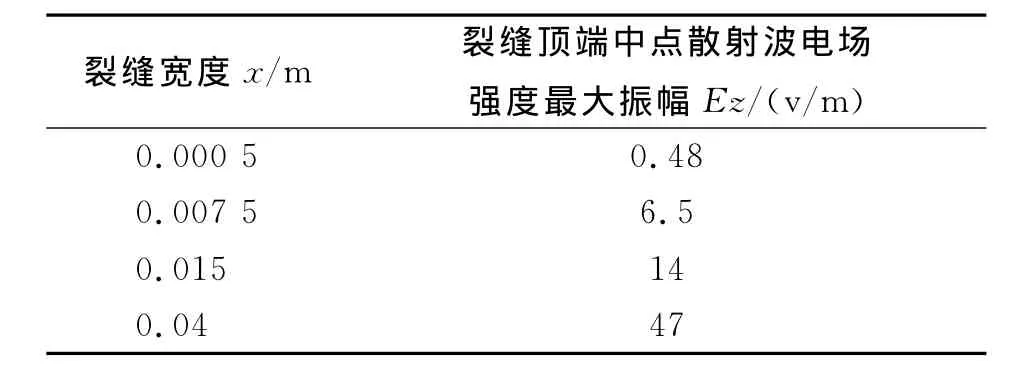
表1 垂直裂缝顶部中点处散射波最大振幅Ez与裂缝宽度x之间的关系

假设雷达天线的灵敏度为k（mv/m），极板最大尺寸为L（m），则雷达天线可检测到的最小信号电平为kL（mv）.假设仪器背景噪声电平为N（mv），当信噪比S/N不小于0.5时，通过多次垂直叠加可有效地提高信噪比，则当kL≥0.5N时，探地雷达仪器可检测到的最小裂缝宽度为x＝kL/1 200（mm）.如中国电波传播研究所生产的雷达天线系统能感应到的最小信号电平为2mv，则此例中，它能够检测到的最小裂缝宽度为1.67μm.因此，采用探地雷达方法完全可以对细小裂缝进行检测，并对其宽度进行定量计算.在实际工作中，可以采用已知宽度和埋深的裂缝进行标定来求取近似比例系数a，再根据雷达仪器的灵敏度和公式（3）即可求取探地雷达在相应介质和相应深度时可检测到的最窄裂缝的宽度.

在实际检测中，上述理论公式的重要意义在于：

1）采用探地雷达可以及早发现堤坝、高速公路结构层、工程构件的隐蔽微裂缝或裂隙，为尽早治理潜在隐患提供了可能；

2）通过不同时间检测剖面上同一裂缝异常的振幅大小对比和是否有新的裂缝出现可以有效地监控构筑物中裂缝的发育情况，为治理、修复或防范工作提供科学依据.

3）通过更深入的研究，有可能利用雷达波振幅的大小来方便快捷地确定隐含裂缝的宽窄，由定性解释上升到定量计算的高度.

3 物理模拟与结果分析

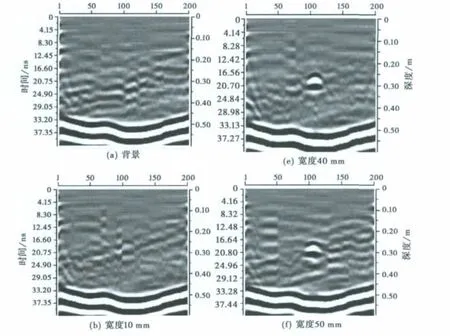
在水中模拟不同宽度垂直裂缝的雷达波响应特征［11］.水槽长2.0m，宽1.5m，深0.5m，在水中放置不同宽度胶木板来模拟不同宽度垂直裂缝，胶木板距水面0.25m.采用中心频率为900MHz的LTD收发一体式探地雷达蝶形天线，其在水中的子波波长λ＝0.037m.天线木质滑轨置于水坑上，天线距水面1cm.天线在滑轨上最大滑动范围为2.0m.记录时窗长度为50ns，空间采样点距为1cm，每张剖面图201个扫描道，所有的测试参数（如增益）均保持不变.不同宽度的垂直裂缝物理模拟剖面图如图5所示.

从图5中可以看出：

1）随着裂缝由窄变宽，其在雷达剖面图上引起的横向异常宽度差异不大，用雷达图像无法直接确定裂缝两侧端点的精确位置，这与探地雷达在水平方向上所能分辨的最小异常体的尺寸为第一菲涅尔带相吻合.

2）随着裂缝由窄变宽，其振幅强度逐渐增强，且续至波相位逐渐增多.为了研究裂缝宽度与其振幅强度之间的关系，对图5中各裂缝的振幅强度进行归一化处理，使其裂缝的最大振幅强度为100，裂缝宽度与其振幅相对大小的对应关系如图6所示.从图6中可以看出振幅强度与裂缝宽度成近似直线关系.

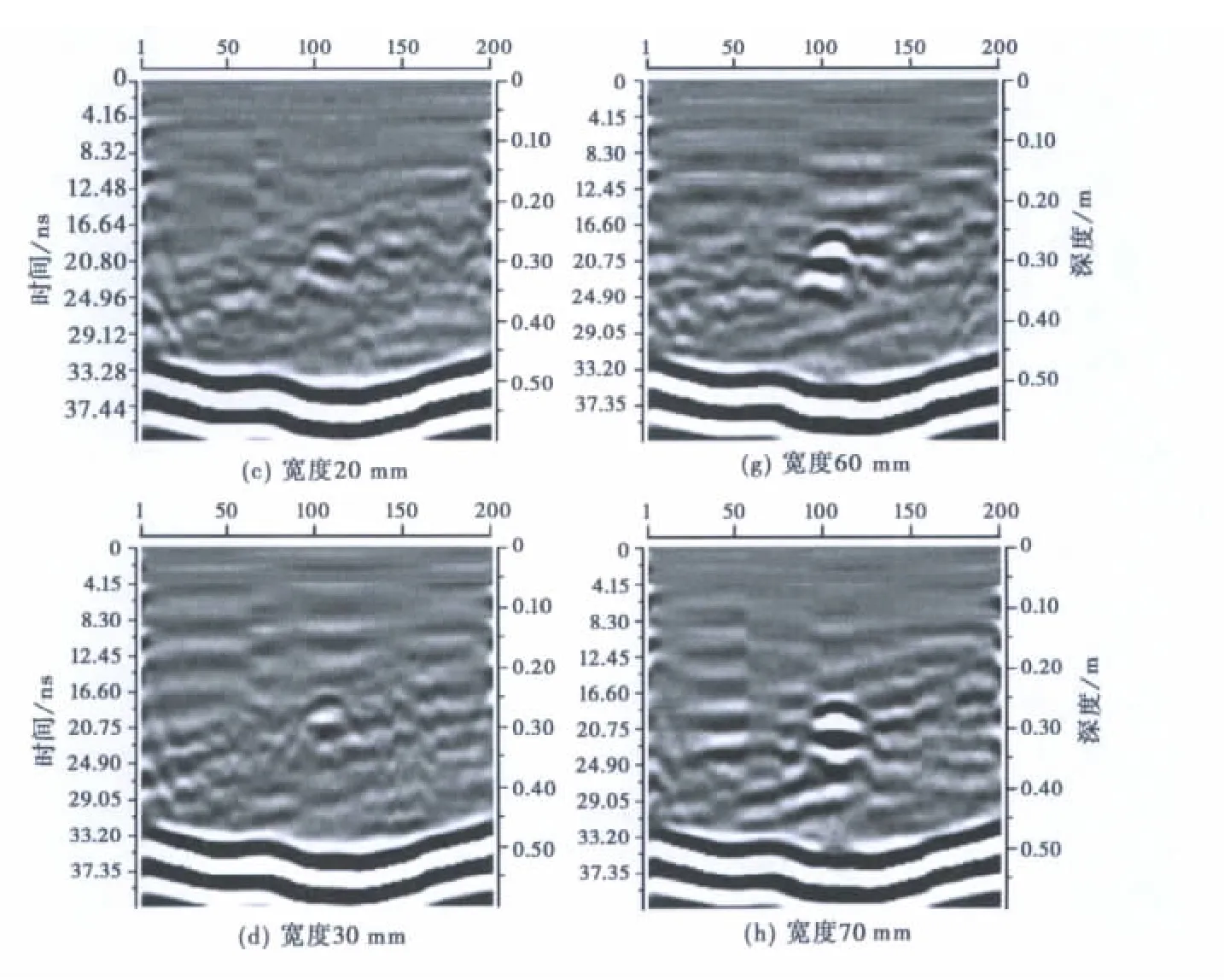
图5 不同宽度裂缝的雷达波响应物理模拟剖面

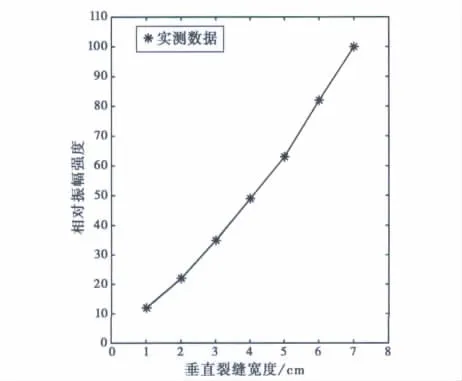
图6 当裂缝宽度小于第一菲涅尔带宽度时，垂直裂缝宽度与振幅强度成近似直线关系

4 结 论

本文基于理论分析、数值模拟和物理实验，研究了裂缝宽度与探地雷达波场的振幅响应之间的关系，主要结论如下：1）随着裂缝的由窄变宽，其对应的振幅强度不断增强，特别是当裂缝宽度小于第一菲涅尔带半径时，裂缝宽度与其振幅强度呈近似直线关系，这为定量化测量裂缝宽度提供了依据；2）当裂缝宽度约等于第一菲涅尔带直径时，其振幅强度达到最大值，超过该宽度后，振幅强度开始有所衰减，然后趋于一个恒定值；3）当裂缝宽度大于第一菲涅尔带直径时，裂缝两侧端点的位置可以从探地雷达图像直接判别；4）研究成果可用于识别地下隐蔽裂缝及定量估计裂缝的宽度.

致谢：文章的物理模拟实验得到了中国电波传播研究所王春和研究员的指导和河南省路通物探科技开发有限公司的大力支持，在此一并致谢.

［1］刘江平，陈 超，侯卫生.浅层地震映像法在堤坝无损检测中的应用［J］.人民长江，2002（5）：26-28.LIU Jiangping，CHEN Chao，HOU Weisheng.Application of shallow layer seismic imaging method for nondestructive detection in dykes［J］.Yangtze River，2002（5）：26-28.（in Chinese）

［2］刘江平，陈 超，许顺芳.垂直裂缝的波场特征及实例［J］.工程地球物理学报，2004，1（1）：55-59.LIU Jiangping，CHEN Chao，XU Shunfang.Wave field character of vertical slit and its instance［J］.Chinese Journal of Engineering Geophysics.2004，1（1）：55-59.（in Chinese）

［3］LIU J，XIA J，LUO Y，et al.Wave field features of shallow vertical discontinuity and their application in non-destructive detection［J］.Journal of Applied Geophysics，2007，62（3）：270-280.

［4］李修忠，卢成明，李波涛.公路路面隐含裂缝的无损检测方法［J］.公路，2005（4）：137-141.LI Xiuzhong，LU Chengming，LI Botao.The nondestructive testing method for hidden cracks in highway pavement［J］.Highway，2005（4）：137-141.（in Chinese）

［5］卢成明，秦 臻，朱海龙，等.探地雷达检测公路结构层隐含裂缝实用方法研究［J］.地球物理学报，2007，50（5）：1558-1568.LU Chengming，QIN Zhen，ZHU Hailong，et al.Practical methods for detection of concealed cracks in highway pavement using ground penetration radar data［J］.Chinese Journal Geophysics，2007，50（5）：1588-1568.（in Chinese）

［6］李成香，强建科，王建军.地质雷达在公路裂缝检测中的应用［J］.工程地球物理学报，2004，1（3）：282-286.LI Chengxiang，QIANG Jianke，WANG Jianjun.The application of ground penetrating radar of highway surface crack inspection［J］.Chinese Journal of Engineering Geophysics，2004，1（3）：282-286.（in Chinese）

［7］杨成林，陈宁生，施蕾蕾.探地雷达在赵子秀山滑坡裂缝探测中的应用［J］.物探与化探，2008，32（2）：220-224.YANG Chenglin，CHEN Ningsheng，SHI Leilei.Application of ground penetrating radar in the exploration of landslide fissures in MT.Zhaozixiu［J］.Geophysical and Geochemical Exploration，2008，32（2）：220-224.（in Chinese）

［8］王国群.不同成因地裂缝探地雷达图像特征［J］.物探与化探，2009，33（3）：345-349.WANG Guoqun.Character instinct analysis of GPR images for underground cracks of different geneses［J］.Geophysical and Geochemical Exploration，2009，33（3）：345-349.（in Chinese）

［9］李廷军，周正欧.探地雷达中双曲线的提取及在波速估计中的应用［J］.电波科学学报，2008，23（1）：124-128.LI Tingjun，ZHOU Zhenou.Extraction of hyperbolic signatures and application for propagation velocity estimation in GPR［J］.Chinese Journal of Radio Science，2008，23（1）：124-128.（in Chinese）

［10］张 波，薛正辉，任 武，等.基于图形处理器的时域有限差分算法研究［J］.电波科学学报，2011，26（1）：108-112.ZHANG Bo，XUE Zhenghui，REN Wu，et al.Acceleration of FDTD algorithm based on GPU computing［J］.Chinese Journal of Radio Science，2011，26（1）：108-112.（in Chinese）

［11］孙 伟，徐 青，蓝朝桢，等.水体的探地雷达成像数值模拟与实验比较研究［J］.电波科学学报，2012，27（3）：620-625.SUN Wei，XU Xing，LAN Chaozhen，et al.Numerical simulation and experimental comparison study of GPR imaging in water body［J］.Chinese Journal of Radio Science，2012，27（3）：620-625.（in Chinese）