推广的几乎可分解的26圈系

蒲利群，方佳，马俊

（1.郑州大学 数学系，河南 郑州450001；2.上海交通大学 数学系，上海200240）

1 基本知识

（X，C）称为阶是n的k圈系，如果C为边不交的k圈集合，且为完全无向图Kn边集的划分［1-8］，其中Kn的顶点集为X，｜X｜＝n.

圈系（X，C）称为可分解圈系，如果C中的圈能够分为若干个集合，每个集合中的元素为边不交的圈，其为完全图Kn的一个2-正则支撑子图，称该集合为一个平行类.

下面给出完全图Kn的可分解圈系谱的存在性定理.

定理1［2］阶为n的可分解的k圈系存在的充分必要条件：n≥k≥3，n和k是奇数，并且k整除n.

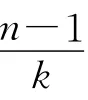
圈系（X，C）称为几乎可分解圈系（almost resolvability cycle system，ARCS）；如果C中k圈能够尽可能多地划分为几乎平行类，并且剩余的k圈顶点互不相交，用kARCS（n）表示.3ARCS（n）［9］和6ARCS（n）［5］已经得到解决.

2 三个基本构造

给出的3个例子是构造26GARCS（n）的基础.其中：V（G）表示图G的点集；Kn表示阶为n的完全图；Km，n表示两个部分的点集数分别为m和n的完全二部图.

例1 26GARCS（65）

令点集V（K65）＝｛ij｜i∈Z13，j＝1，2，3，4，5，有40个几乎平行类.13个几乎平行类是在模13下循环，其下标被固定为

令点集V（K65／K13）＝｛ij｜i∈Z13，j＝1，2，3，4，5｝，点集H＝｛i1｜i∈Z13｝，其中：H为阶 13的洞，并且H⊂V（K65／K13）.如果K65／K13的边集能够划分成26圈系，称这个圈系为阶65，洞13的26圈系.

集合F1含下面的两个几乎平行类，该平行类在模13下循环，其下标固定为

其中：F1中k圈与洞H中的点相交，但是F2∪S中所有的26圈与洞H中的点不相交.

例3 26GARCS（117）

令V（K117）＝｛ij｜i∈Z13，j＝1，2，3，…，9｝｝.该圈系含有65个几乎平行类和一个短平行类，其中每一类包含4个26圈.

两个几乎平行类在模13下循环，其下标是固定的，即

以上26个几乎平行类使用了所有的纯差和部分的混差，剩余的混差下标，如表1所示.因下标相同的两个混差可构造一个26圈，表1由包含4对下标的列和包含一对下标列组成.

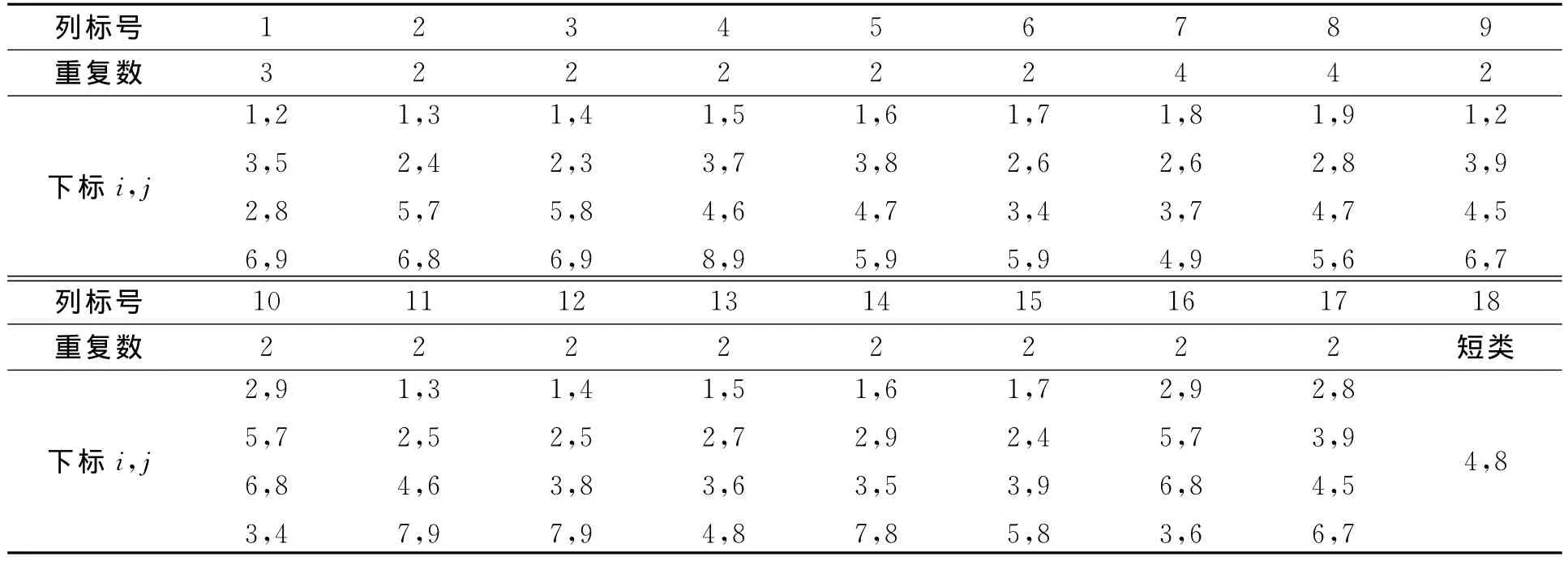
表1 剩余混差的下标Tab.1 Remaining mixed difference subscript

使用相同的方法可构造其他所有的几乎平行类.

2 构造26GARCS（n）s

为了证明主要的结果，需要定理2.

定理2［7］二部图K2m，2m能划分成2k圈的平行类的充分必要条件是2k｜2m，但图K6，6不能划分成6圈的平行类.

下面给出26GARCS（52t＋13）的构造，其中：2t≥6.

Ⅲ）现在已经穷尽了3）中的所有26圈，剩余的圈集有1）中的14个几乎平行类，F2中12个几乎平行类和对每一个hi，2≤i≤t的S中的短平行类.由于F2中的几乎平行类与洞∞中的点不相交，将1）中12个几乎平行类与每一个洞hi，i≥2，F2中的12个几乎平行类配对.则得到C中的12个几乎平行类.

Ⅳ）目前剩余的是1）中的两个几乎平行类和每一个洞hi，i≥2中的短平行类.将1）中的一个几乎平行类与每一个洞hi，i≥2中的短平行类配对.则得到C中的一个几乎平行类包含t＋1个26圈.最后剩余的是1）中的一个平行类包含两个圈，构成短平行类.

定理3 阶为n的推广的几乎可分解的26圈系的谱为n≡13（mod 52）.

证明 例1，3考虑了阶为65和117的情况.52t＋3的构造给出了每一个阶为n≡13（mod 52）（n≥117）的几乎可分解的26圈系.因此，定理得证.

［1］ ALSPACH B，GAVLAS H.Cycle decompositions of and［J］.J Combin Theory B Ser，2001，81（1）：77-99.

［2］ SAJNA M.Cycle decompositions：Complete graphs and fixed length cycles［J］.J Combin Designs，2002，10（1）：27-78.

［3］ ALSPACH B，SCHELLENBERG P J，STINSON D R，et al.The Oberwolfach problem and factors of uniform odd length cycles［J］.J Combin Theory A Ser，1989，52（1）：20-43.

［4］ PIOTROWSKI W L.The solution of the bipartite analogue of the Oberwolfach problem［J］.Discrete Math，1991，97（3）：339-356.

［5］ VANSTONE S A，STINSON D R，SCHELLENBERG P J，et al.Hanani triple systems［J］.Israel J Math，1993，83（3）：305-319.

［6］ LINDNER C C，MESZKA M，ROSA A.Almost resolvable cycle systems：An analogue of Hanani triple systems［J］.J Combin Designs，2009，17（5）：404-410.

［7］ PETER A，ELIZABETH J B，HOFFMAN D G，et al.The generalized almost resolvable cycle system problem［J］.J Combin Math，2010，30（6）：617-625.

［8］ DEJTER I J，LINDNER C C，MESZKA M，et al.Almost resolcable 26-cycle systems［J］.J Combin Math Combin Computing，2007，63（2）：173-182.

［9］ LINDNER C C，RODGER C A.Design theory［M］.Bocaraton：CRC Press，1997：137-159.