圆排列包装问题最优解解析

杨金勇，宋海洲

（华侨大学 数学科学学院，福建 泉州362021）

近年来，组合优化问题引起越来越多的关注，如文献［1］用混合遗传算法求解0-1背包问题，文献［2］用蚁群算法解决TSP问题，文献［3-6］用回溯法、蚁群算法求解圆排列问题.目前，圆排列研究得最多的问题是如何求解最小长度，然而，在生产生活中也会遇到下面这种情况，生产统一大小的盒子，要求这种盒子能够装下以任何一种排列顺序排进该盒子的n个大小不全相等的圆，且盒子长度尽可能的小.本文把这种问题称为圆排列包装问题，并对此进行研究.

1 圆排列包装问题的数学模型

圆排列包装问题描述为找一个矩形框，将n个大小不全相等的圆以任何一种排列顺序排进该矩形框后，都能保证这n个圆与矩形的底边相切，且要求这种矩形框长度最小.

下面给出一些集合和相关长度的定义.

定义1 给定n个圆C1，…，Cn，其圆心的横坐标分别为x1，x2，…，xn，半径分别为R1，R2，…，Rn，R1≤R2≤…≤Rn，且R1＜Rn.定义下面4个的集合S，T，Q，P.

1）S＝｛w｜（w＝i1，i2，…，in）为1，…，n的n级排列｝.

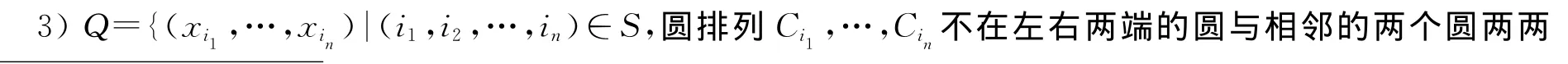
2 圆排列包装问题的最优解的性质

定理1 模型（2）中的所有最优解中必存在一个最优解l，使得该最优解对应的圆排列的圆心的横坐标构成的向量属于L.

图1 圆排列Fig.1 Circle permutation

综上所述，假设不成立，故定理得证.

3 模型的转化及求解

由定理1可知：集合T必存在模型（2）的一个最优解l，使得对应圆心的横坐标向量（xk1，xk2，…，xkn）∈T.因此，对模型（2）可进一步转化为

对于模型（3），得到了如下主要结果.

定理2l＝（n，n-1，n-2，…，3，2，1）为模型（3）的一个最优解.

为了证明定理2，先求解下面的模型，即

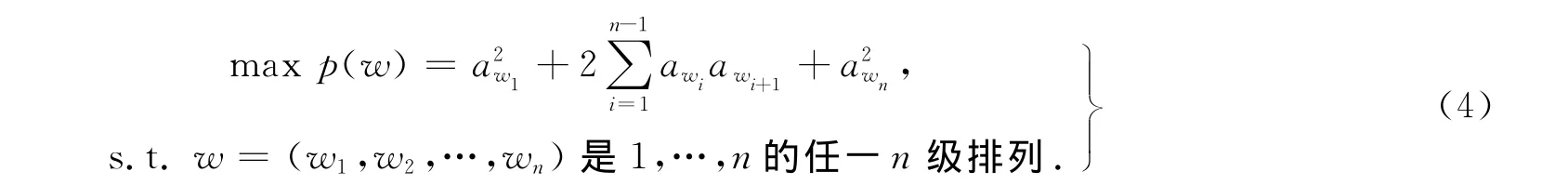
其中：a1≤a2≤…≤an，a1＜an.

对于模型（4），有如下定理.

定理3l＝（n，n-1，n-2，…，3，2，1）为模型（4）的一个最优解.

为了证明定理3，先给出一些引理及定义.

易证如下3个引理成立：

由命题2及命题3易知定理2成立.

4 应用举例

［1］ 宋海洲，魏旭真.求解0-1背包问题的混合遗传算法［J］.华侨大学学报：自然科学版，2006，27（1）：17-19.

［2］ 徐强，宋海洲，田朝薇.解TSP问题的蚁群算法及其收敛性分析［J］.华侨大学学报：自然科学版，2011，32（5）：589-591.

［3］ 王晓东.计算机算法设计与分析［M］.北京：电子工业出版社，2001：179-181.

［4］ 高尚，杨靖宇，吴晓俊，等.圆排列问题的蚁群模拟退火算法［J］.系统工程理论与实践，2004（8）：102-106.

［5］ 章义刚，贾瑞玉，张燕平，等.快速蚁群算法求解圆排列问题［J］.计算机技术与发展，2007，17（8）：48-50.

［6］ 章义刚，王会颖.改进蚁群算法求解圆排列问题［J］.机电工程，2008，25（5）：92-95.