求解一类新的二次规划问题的时滞投影神经网络方法

刘德友，牛九肖

（燕山大学 理学院，河北 秦皇岛066004）

常见的二次规划问题

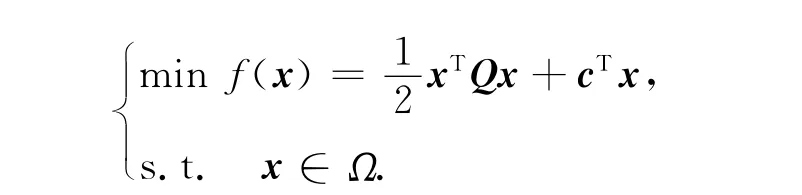
其中：x∈Rn是决策变量；c∈Rn；Ω∈Rm是闭的凸集.约束二次规划已经应用于许多科学和工程领域，如回归分析、信号和图像的处理、制造业、优化控制和模式识别等.在过去的十年里，神经网络被认为是解决二次规划问题的一种最有前景的方法［1-5］.目前，已经有一些投影神经网络技术解决了二次优化问题.然而，以往所研究的二次规划仅仅停留在凸二次规划上，即矩阵Q为正定或者半正定的［6-7］，而在许多情况下，二次规划并不是凸的，也就是说矩阵Q可能不是正定或半正定的.此外，在许多实际应用中，最优化问题还有一个自然时变亟待解决，时间延时可能导致震动现象或者网络的不稳定.本文研究一类新的二次规划问题最优解的稳定性，推广了以往所研究的凸二次规划问题，

1 模型的提出

所研究的二次规划问题为

式（1）中：x∈Rn是决策变量；Q∈Rn×n是亚（半）正定矩阵；c∈Rn；Ω∈Rm是闭的凸集.

为了方便讨论，给出亚（半）正定矩阵的定义.

式（10）中：τ≥0是时间延迟；φ（t）在［-τ，0］上是连续的.

显然，神经网络式（10）的平衡点和二次规划问题（1）的解是一致的.因此，时滞神经网络在其平衡点是稳定的，那么网络的输出就是式（1）的解.

下面给出一些相关的定义和引理.

引理1Q为对称的亚正定矩阵，当且仅当Q为正定矩阵.

由此可见，以前所研究的严格凸的二次规划是本文所研究二次规划的一种特例.

2 稳定性分析

根据引理2可以得到‖x（t）‖≤（（1＋τ）‖φ‖＋β1‖x＊‖T）exp（β1t），t∈［0，T］.所以，x（t）在［0，T］上是有界的.根据引理4，式（10）在区间［0，＋∞）上存在一个连续解x（t）.

定理2 时滞神经网络（10）全局渐近稳定于二次优化（1）的解，当矩阵Q是一个亚（半）正定矩阵.

证明 假设x＊是（10）的平衡点，考虑如下的李亚普诺夫函数

3 数值举例

例1 考虑如下二次规划问题

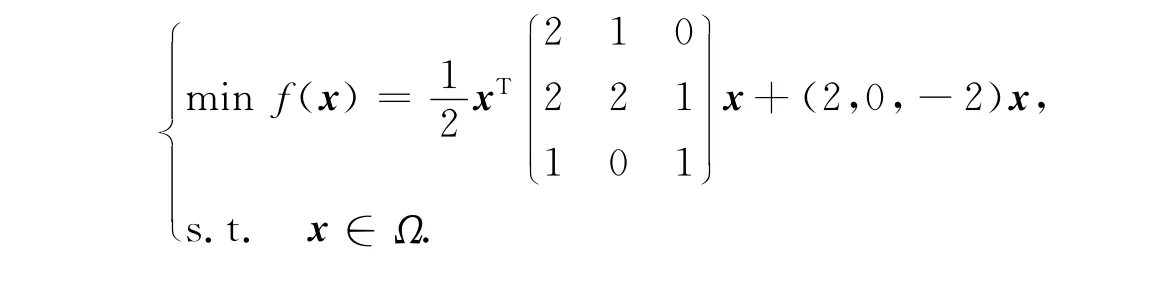
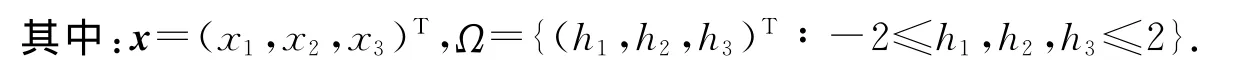
利用5个初始值来测验神经网络，所有的结果显示出神经网络收敛到问题的最优解，仿真结果如图1所示.对时滞神经网络和非时滞的神经网络进行了对比，结果如图2所示.

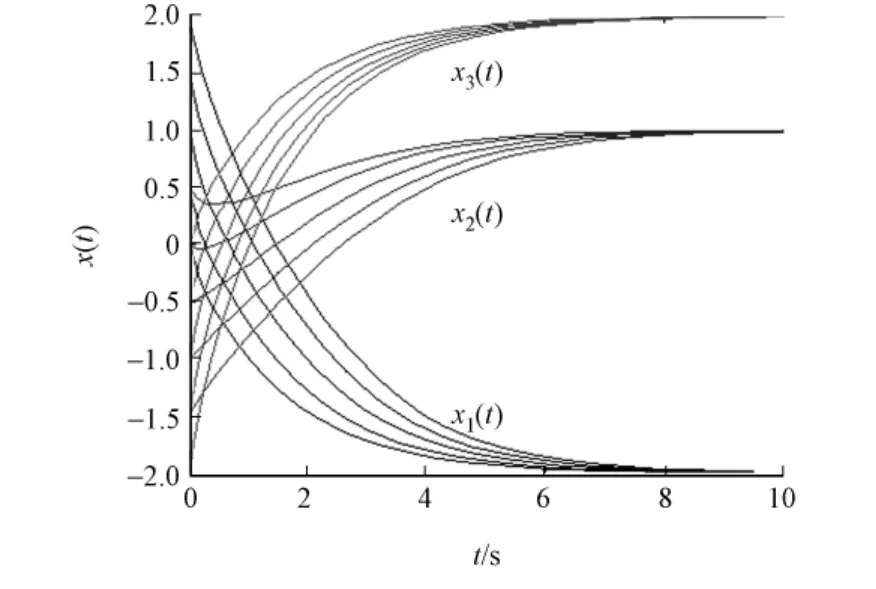
图1 神经网络仿真结果Fig.1 Simulation results of the neural network

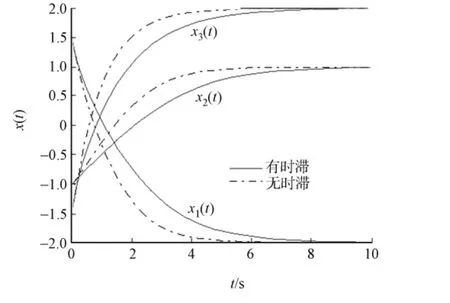
图2 神经网络的轨迹对比Fig.2 Comparison of the trajectory of neural network

例2 考虑如下二次规划问题：

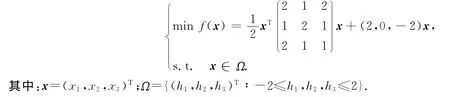
令时间延迟t＝0.25，根据定理3，神经网络（10）的平衡点是全局渐近稳定的，并且收敛于二次规划的最优解x＊.因此，利用7个初始值来测验神经网络，所有的结果显示出神经网络收敛到问题的最优解，其仿真结果如图3所示.相应的，对时滞神经网络和非时滞的神经网络进行对比，结果如图4所示.

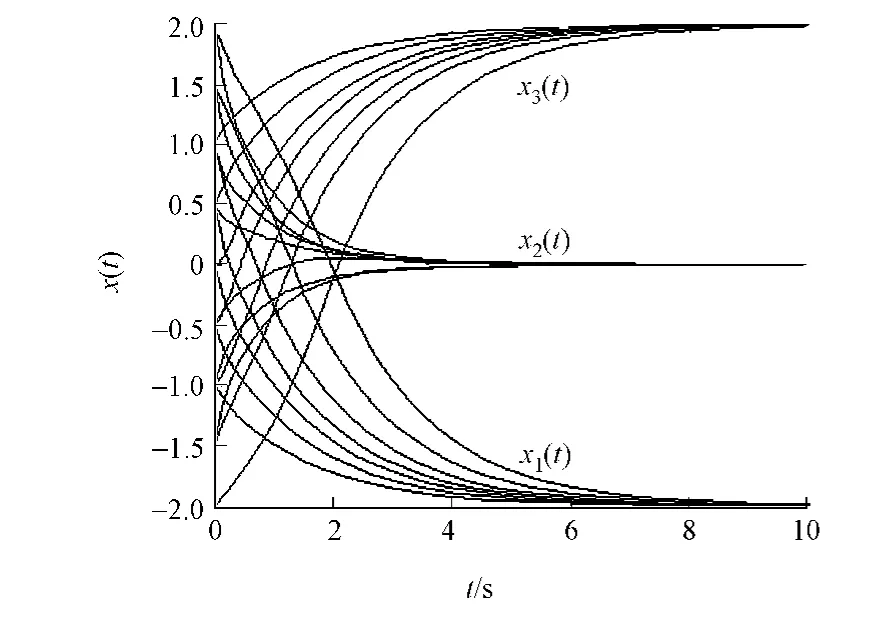
图3 神经网络仿真结果Fig.3 Simulation results of the neural network

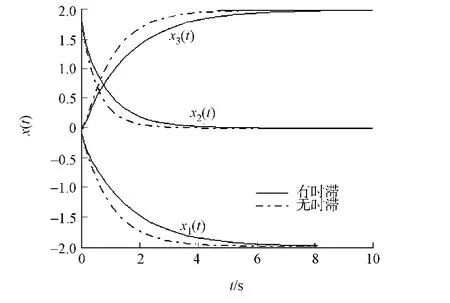
图4 神经网络的轨迹对比Fig.4 Comparison of the trajectory of neural network

4 结论

研究一种新的二次规划最优解的稳定性，是对以前凸规划的进一步深入推广，给出了解决此类问题的投影时滞神经网络模型，以及鞍点定理与最优解的关系.同时，文中给出了判定平衡点全局指数稳定的充分条件，并借助李亚普诺夫函数给出系统全局渐近稳定的新的充分条件.最后，用数值举例说明了所给系统的有效性.

［1］ XIA You-shen，FENG Gang，WANG Jun.A recurrent neural network with exponential convergence for solving convex quadratic program and related linear piecewise equations［J］.Neural Networks，2004，17（7）：1003-1015.

［2］ XUE Xiao-ping，BIAN Wei.A project neural network for solving degenerate convex quadratic program［J］.Neurocomputing，2007，70（13／15）：2449-2459.

［3］ LIU Qing-shan，CAO Jin-de，Global exponential stability of discrete-time recurrent neural network for solving quadratic programming problems subject to linear constraints［J］.Neurocomputing，2011，74（17）：3494-3501.

［4］ TAO Qing，CAO Jin-de，Demin Sun.Neural network for quadratic programming problems［J］.Applied Mathematics and Computation，2001，124（2）：251-260.

［5］ HASAN G O，NEZAM M A.An efficient simplified neural network for solving linear and quadratic programming problems［J］.Applied Mathematics and Computation，2006，175（1）：452-464.

［6］ 李洁坤，丁明智，虞继敏.非线性时滞细胞神经网络稳定性分析［J］.郑州大学学报：理学版，2010，42（3）：54-58.

［7］ 杨华芬，杨有，尚晋.一种改进的进化神经网络优化设计方法［J］.郑州大学学报：工学版，2010，31（5）：116-120.

［8］ YANG Yong-qing，CAO Jin-de.A feedback neural network for solving convex constraint optimization problems［J］.Applied Mathematics and Computation，2008，201（1／2）：340-350.

［9］ BERTSEKAS D P.Parallel and distributed computation：Numerical methods［M］.Englewood Cliffs：Prentice-Hall，1989.

［10］ HALE J K，VERDUYN-LUNEL S M.Introduction to functional differential equations［M］.New York：Springer，1993.