B掺入CuΣ5晶界间隙位性质的第一性原理研究*

孟凡顺 赵 星 李久会

(辽宁工业大学理学院，锦州 121001)

(2013年1月14日收到;2013年1月28日收到修改稿)

1 引言

近年来，由于超高纯度材料制备和材料中微量元素测试技术的提高，金属中微量杂质对金属力学性能的影响已广为人知[1].杂质在晶界处的偏析导致晶粒间结合的强化与弱化直接关系着金属材料的力学性能[2,3].比如B，C，N，Mo，W等常被用作有益提升力学性能的元素，P，S，Sn等元素的掺入却能降低材料的力学性能[4].Cu及其合金因其良好的导热、导电率及较高的强度在各个领域被广泛应用.Cu材料在制备过程中，因工艺条件的限制，往往会形成各种缺陷(如晶界、位错等)，直接影响着材料的宏观力学表现[5].B能有效的阻止Sb向Cu晶界处偏析，在改善金属晶粒间结合方面也具有极好的记录[6].因此研究B在Cu晶界处的掺杂有重要意义.

Ogata等[7]采用第一性原理方法研究了铜、铝晶体的理想剪切强度，阐明了铜剪切强度低于铝的原因是在软化前有较小的扩展形变范围.Lu等[8]在实验上测得了不同厚度Cu纳米孪晶的拉伸强度，发现样品拉伸强度与孪晶厚度在一定范围内存在反比关系.Geng等[9,10]基于第一性原理计算发展了偏析元素对晶界结合影响的唯象模型并有他人的工作[11,12]验证了其合理性.Freeman等[13,14]利用Rice-Wang热力学模型[15]应用第一性原理方法研究了P，S，B等杂质在Fe和Ni晶界中的作用.Ittermann等[16]从实验上发现B能以替换与间隙掺杂方式植入到Cu晶界处，而且以替换方式植入的机理为直接交换机理而非空位机理;Stockmann等[17]的研究进一步表明，B与其近邻由Cu组成笼状结构的定域振动触发了该直接交换机理.Lozovia等[6]使用标准密度泛函理论研究了B在晶界处和晶体中掺杂的行为，他们基于Rice-Wang热力学模型获得了浓度为0.5—1.5 ML B的掺入都加强了Σ5{310}[001]晶界的结合，但未给出B对晶界在拉伸过程产生的影响.最近第一性原理拉伸实验被用来研究各种有杂质偏析晶界的原子结构、电子结构及力学性质[2,3,18-23]，但据笔者所知，到目前为止有关B掺杂到CuΣ5{310}[001]晶界在拉伸和压缩过程中晶界结构和力学性能等的工作尚未见发表.本文利用第一性原理方法对CuΣ5{310}[001]晶界及有B掺杂到该晶界的拉伸和压缩过程进行了模拟计算，得到了一些有意义的结果.

2 计算方法

计算采用重合位置点阵(Coincident Site Lattice，CSL)模型[24].在CSL模型中，由不同取向晶体中某些位置相互重合的原子组成一个新的点阵，即CSL点阵，并以一参量“重合位置密度”表征CSL的特征.重合位置密度指CSL的阵点占原有点阵阵点的分数，以符号1/Σ表示.符号Σ5{310}[001]表示在错配方向上，两个晶粒有1/5的阵点位置重合，[001]和(310)分别表示错配方向与晶界平面.本文所用的晶界超晶胞为层晶模型，它由有1个共用面的两个13层晶粒组成，并在两侧各添加了6的真空层，其结构如图1(a)所示，这与Sørensen等[25]及扫描隧穿电子显微镜所得铜Σ5晶界结构[26]相似.

计算过程中固定两侧最外各4层原子的相对位置，使其保持铜fcc晶体的结构，其他原子位置则完全弛豫.同时为节省计算量，忽略了泊淞效应[18,19,27,28].在单轴拉伸、压缩晶界时采用的方法与文献[3]相同，但因本文固定了更多的外层原子，使模拟块体环境更充分，具体方法为：以很小的步幅移动最外侧的固定原子.在寻找最低能量尺寸过程中，步幅为0.1其他过程步幅则为0.2应变ε定义为：ε=(d-d0)/d0，其中d0为层晶模型[10]方向最低能量结的厚度，d为该方向形变过程中的厚度，在压缩形变中，应变ε为负值.该方法模型尺寸在形变方向上不易过大.

图1 (a)Σ5{3 10}[001]晶界超晶胞模型;(b)拉伸断裂后的超晶胞模型;(c)与(d)分别是拉伸断裂后的上、下部分

本文的第一性原理拉伸、压缩计算应用的是基于密度泛函理论(DFT)结合缀加投影平面波方法(PAW)的VASP软件包[29,30]，交换关联势采用广义梯度近似(GGA)框架下的Perdew-Burke-Ernzerhof(PBE)泛函[31]处理.需要注意的是，与实验值相比，GGA近似会高估晶格常数而低估结合能，LDA恰好与之相反[32,33].经过测试，平面波截断能为320 eV，采用7×4×1的Monkhorst-Pack型K点网格，结构弛豫采用共轭梯度法，能量收敛标准为10-5eV，作用力小于0.02 eV/.采用上述方法，计算得到的Cu的晶格常数为3.6345，体模量为142.4 GPa，与实验值符合得较好.

表面能是具有相同原子个数的块体与层晶模型单位面积能量之差，本文按照下式计算：

晶界形成能是具有相同原子个数的块体与含有晶界层晶模型的单位面积能量之差.其计算方法如下式所示：

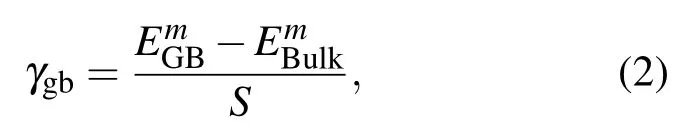
与测试计算可比较的结果汇总于表1和表2.可见本文所用方法较为可靠.

表1 纯Cu晶体的晶格常数a0，体模量B，(310)表面的表面能γFS及其他理论和实验方法获得的结果

表2 CuΣ5{310}[001]晶界的形成能γgb，断裂能Wsep及它们由其他方法获得的 CuΣ5，CuΣ9，CuΣ19晶界的结果

3 结果和讨论

3.1 B的掺杂位置

在CuΣ5晶界处有3个位置可以替换或掺入1个硼原子：松位(Loose site)替换，紧位(Tight site)替换及间隙位(Interstitialsite)掺杂，分别与图1(a)中1，2，3位置相对应.将B按照上述三种方式植入，以前文所述的压缩、拉伸方法，可获得不同掺杂位置的最低能量结构所对应的尺寸(如图2所示)，还可得到拉伸与压缩过程中不同应变下的结构、能量、应力等方面的重要信息.与清洁的CuΣ5晶界相比，替换松位或掺杂到间隙位1个B原子，晶胞尺寸在[10]方向膨胀约2%;当替换紧位Cu时，该方向晶胞尺寸收缩约1%.通过计算比较发现，当硼原子以间隙位掺杂方式植入到CuΣ5晶界处时，B原子结合能最高，体系总能量最低.因此间隙位是掺杂的最佳位置.

图2 B掺杂到Σ5{310}[001]晶界后超晶胞能量随[10]方向尺寸的变化曲线(图中横坐标以清洁Cu晶界的应变为标准.3.52 eV为铜fcc晶体中1个原子的平均结合能)

3.2 Griffith断裂能与理论韧性

Griffith断裂能、理论韧性和理论拉伸强度等参量是表征材料力学性能的物理量[40].通过对晶界的第一性原理拉伸试验，可得到晶界的上述三个参量.其中Griffith断裂能和理论韧性可由系统能量获得.

图3(a)给出了清洁CuΣ5晶界与有B掺杂到间隙位的CuΣ5晶界(即清洁Cu晶界与有B掺杂Cu晶界，下同)应变-能量曲线.对于清洁Cu晶界，当应变为12.98%时能量增速突然放缓，在应变为15.71%之后体系能量趋于稳定;对于有B掺杂Cu晶界，能量在应变为18.19%达到最大值，之后发生陡降，应变为20.89%之后趋于稳定.

按照Griffith理论，断裂能定义为没有塑性形变下劈开脆性材料所做的功.材料从晶界劈开后，晶界被破坏的同时形成两个自由表面.因此断裂能可表达为单位面积内晶界能量(γgb)与由该晶界断裂形成的两个自由表面的能量(2γs)之差，如下式所示：

从图3(a)可得，清洁Cu晶界与有B掺杂Cu晶界的断裂所需能量分别约为2.97 eV与3.86 eV，因此相应的Griffith断裂能分别为2.24 J/m2，2.88 J/m2，均小于Lozovoi等[6]采用LDA近似的结果：3.35 J/m2，3.81 J/m2，这是由于文献 [6]的表面能大于本文所致.二者均表明B的掺入使晶界断裂能增大.Griffith断裂能仅与初始能量和完全断裂后的能量相关，因此不能充分来描述材料拉伸过程中的性质，而理论韧性则能进行很好的补充描述.材料的理论韧性定义为断裂时的应变能密度，即拉断系统所需要的能量除以其体积.对于清洁Cu晶界与有B掺杂Cu晶界，将其拉断所需的能量分别约为2.81 eV和4.20 eV，其相应体积分别为358.023与366.373，因此理论韧性分别为1.26 GPa，1.84 GPa.可见有B掺杂Cu晶界的理论韧性得到明显增强.

3.3 理论拉伸强度和断裂特性

图3(b)给出了拉伸和压缩过程中清洁Cu晶界与有B掺杂Cu晶界在[10]方向的应变-应力曲线.对于清洁Cu晶界，随着应变增大，应力随之增大，当应变达到12.98%时，拉伸方向的应力达到最大值9.45 GPa，当应变达到15.71%，应力急剧下降到2.84 GPa，之后应力缓慢降低.因此清洁Cu晶界的理论拉伸强度为9.45 GPa，对应应变为13%左右.晶界断裂应发生在应变16%之后.对于有B掺杂Cu晶界，随着应变增大，应力也随着上升，当应变为18.19%时，拉伸方向应力达到最大值11.02 GPa，之后应力急剧下降至应变为20.89%的1.62 GPa，晶界断裂应发生在此之后.二者均与图3(a)中应变-能量曲线的变化规律相对应.从图3(b)还可得到，压缩过程中，形变在小于-7.5%时，B原子的掺入未产生影响，当应变大于-7.5%时，与清洁Cu晶界相比，有B掺杂晶界的应力增大趋势减缓，但这种影响显然是非常微弱的.由此可见，由于B原子的加入，使得清洁Cu晶界的理论拉伸强度增大了16.6%，临界形变提升40.0%左右，显著地提高了CuΣ5晶界的理论拉伸强度，但抗压性能未产生显著变化.

值得注意的是，本文所得的Cu晶界的理论拉伸强度明显大于Cu纳米孪晶[8].这主要是由于本文未考虑除晶界以外的其他缺陷，而这些缺陷特别是位错，将大幅降低材料的拉伸强度[39,40].另外，忽略泊松效应也是理论拉伸强度较高的一个原因.在Lu等[41]研究AlΣ9晶界理论拉伸强度时亦出现了理论值(9.50 GPa，21%)大于实验(长10.0µm，厚0.66µm的单晶铝纤维样品)值(2.25 GPa，2.9%)的情况.Geng等[3]在NiΣ3晶界拉伸过程研究中专门讨论了泊松效应对拉伸实验的影响.

偏析能(ΔE)定义为掺杂原子从块体扩散到晶界位置所需要的能量.根据Rice-Wang热力学模型[15]，晶界处偏析能 (ΔEGB)与表面偏析能 (ΔEFS)的差值 (ΔEGB-ΔEFS)可以定性描述杂质对晶界作用的加强或削弱.利用计算晶界断裂能时所用的近似，可得B在CuΣ5掺杂的ΔEGB-ΔEFS为-0.89 eV/atom，与Lozovoi等[6]的结果-0.56 eV/atom接近，均表明B的掺杂加对CuΣ5晶界的结合起到了加强作用.第一性原理拉伸实验结果与此定性预测一致.

图3(c)与(d)分别给出了由第一性原理拉伸和压缩试验得到的Cu晶界与有B掺杂Cu晶界在三个方向的应变-应力曲线.在拉伸时，由于泊松效应的存在，使得晶胞沿[10]方向产生伸长或压缩形变的同时，在垂直于伸长方向的[130]与[001]方向需产生相应的压缩或伸长形变.在计算中固定了晶胞在上述两个方向的尺寸，相当于对晶界也同时在这两个方向施加了与[10]方向相同的作用，所以在平行于晶界平面的[130]与[001]方向也产生了应力.从图3(c)与(d)可看出，在压缩的初始阶段，上述两个方向应力的变化规律与[10]相似，都可用胡克定律来描述.由于本文模拟计算所用晶界模型尺寸较小并忽略了泊松效应及应变过程中可能出现的层错等缺陷，因此晶界在断裂以前、压缩形变小于20%阶段均处于弹性形变区.随着压缩应变增大，[001]方向的应力增速高于其他两个方向.对于清洁Cu晶界，如果继续进行压缩试验，在应变超过-28%后，[001]方向的应力将超过[10]方向的应力.这表明较大压缩形变对晶界造成的影响将小于压缩产生的剪切形变对晶界造成的影响，易有位错发射.

图4(a)—(g)给出了清洁Cu晶界拉伸过程中应变为 -17.07%，-11.61%，0%，12.98%，14.34%，15.71%，30.74%沿[001]方向的晶界结构图.可见清洁Cu晶界断裂发生在晶界界面处.有B掺杂Cu晶界的应变为-18.19%，-11.45%，0%，18.19%，19.54%，20.89%，28.98%沿[001]方向的晶界结构如图4(h)—(n)所示.可见有B掺杂Cu晶界断裂发生在晶界界面附近的原子层，这与Lozovia等[6]将B置于Cu(310)表面弛豫后B进入Cu表面下层的基体相一致.在压缩及断裂前的拉伸过程中，两种晶界结构均随形变均匀变化.

3.4 键长和原子滑动

为了进一步了解拉伸过程中B掺杂对Cu晶界力学性能的影响及断裂过程结构变化的细节，本文分析了在拉伸和压缩作用下晶界附近各键长变化及晶界处原子在晶界平面内滑动的信息.

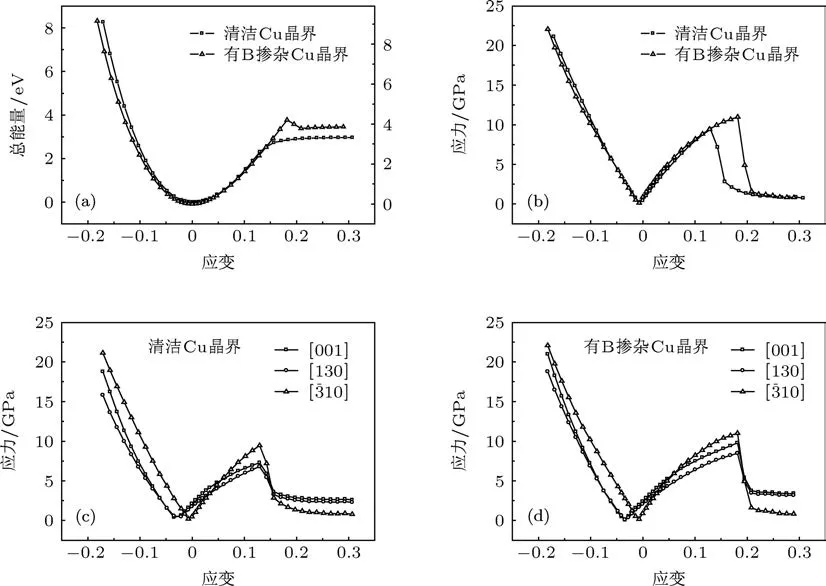
图3 (a)清洁Cu晶界与有B掺杂Cu晶界形变过程中应变-总能量关系曲线;(b)清洁Cu晶界与有B掺杂Cu晶界形变过程中[10]方向应变-应力关系曲线;(c)清洁Cu晶界形变过程中应变-应力关系曲线;(d)有B掺杂Cu晶界形变过程中应变-应力曲线

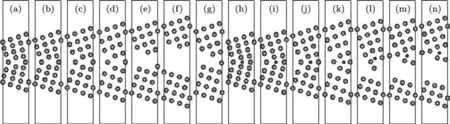
图4 (a)—(g)表示清洁Cu晶界形变过程中应变为-17.07%，-11.61%，0%，12.98%，14.34%，15.71%，30.74%的几何构型图.(h)—(n)表示有B掺杂Cu晶界形变过程中应变为-18.19%，-11.45%，0，18.19%，19.54%，20.89%，28.98%的几何构型图(灰色大球为Cu，黑色小球为B)

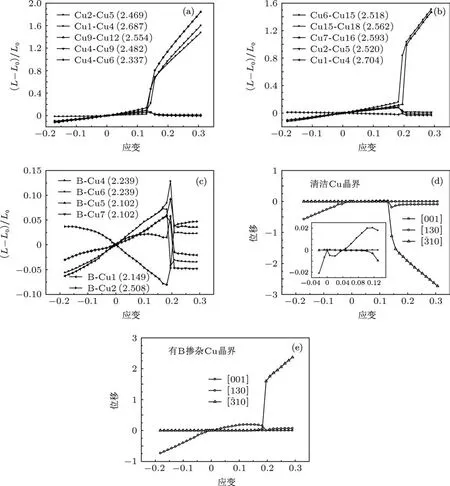
图5 (a)与(b)分别表示清洁Cu晶界及有B掺杂Cu晶界中晶界及附近原子形变过程中键长-应变曲线;(c)表示有B掺杂Cu晶界中B与近邻Cu键长-应变曲线;(d)与(e)分别表示清洁Cu晶界与有B掺杂Cu晶界在形变过程中Cu2在晶界平面内3个方向的应变-位移曲线(位移单位为)(a)—(c)中各键最低能量对应键长在括弧中给出，单位为)

图5(a)与(b)给出了晶界近邻原子键长随应变的变化曲线.纵坐标为相对键长，即[(L-L0)/L0]，其中L0为能量最低结构的各原子键长(在括弧中给出)，L为形变发生后的键长.对于清洁Cu晶界，使用Cu2-Cu5，Cu1-Cu4及Cu4-Cu6的键长标记晶界，使用Cu9-Cu4键长标记晶界与近邻原子，使用Cu9-Cu12键长标记非晶界处.从图5(a)可看出，随着应变的增大，各原子间的距离都在逐渐增大，当应变增大到12.98%时，晶界处原子间距离急剧增大，远离晶界处的原子间距减小到与初始结构相近的距离.这表明断裂发生在了键长陡增的原子间.当形变大于15.71%时，晶界处原子间距随着应变的增大均匀增大，这意味着原本成键的两个原子分别处于晶界断裂后的不同部分.Cu9-Cu4与Cu9-Cu12保持固定间距不变，这表明它们的相对位置没有变化，处于断裂后晶界的同一侧.仔细观察应变-键长的变化规律发现，Cu1-Cu4间距变化最为缓慢，形变从-15.7%到11.7%，其间距变化量仅为-1.4%到2.2%，该键较“硬”，当应变大于14.43%时，Cu1-Cu4间距率先均匀变化，表明断裂首先发生在了Cu1-Cu4间，其他Cu-Cu键之后随之断裂.由此可见，Cu1-Cu4键在维持晶界强度方面起到了特别重要的作用.Cu4-Cu6间距变化最为快速，在上述两个应变下的间距变化量分别为-11.8%和14.0%，该键较“软”，这将从电荷密度分布方面做进一步分析.在压缩过程中，Cu9-Cu12与Cu9-Cu4表现出相似的变化特征，但在拉伸至晶界断裂前，后者间距增大速率高于前者且与Cu2-Cu5变化规律相似.采用相似的方法，分析有B掺杂晶界应变键长变化曲线可知，标记晶界结构的Cu1-Cu4与清洁晶界性质相同，键较“硬”，但是随应力变化的趋势却截然相反，虽然这个不同是很微小的.Cu6-Cu15与Cu7-Cu16间键长的突然增大标志着晶界的断裂.图5(c)给出了拉伸过程中B原子与所有近邻Cu的键长随应变的变化曲线.大部分B-Cu的距离会随着压缩而减小，随拉伸而增大，但B-Cu2却表现出了截然不同的趋势，这是由于在压缩或拉伸过程中，Cu2位置变化不大，而其余原子则与B一起沿[130]方向产生不同程度的滑动.压缩与拉伸过程中，B与近邻Cu间的距离变化始终在13%以内，表明在此过程中近邻的Cu始终与B保持在同一区域，结构相对稳定.

清洁Cu晶界中Cu1在三个方向的位移应变曲线在图5(d)中给出.压缩过程中，Cu1沿[0]方向移动，以释放在该方向因保持尺寸而积累的应力.在拉伸过程中，Cu1在向的平衡位置处晃动，而后随着应变的增加而沿该方向缓慢移动，在应变为11.61%时该位移为0.02，接着由于Cu1-Cu4键的断裂使得Cu1快速被下半部分的基体原子拉向[方向，并产生了0.19左右的位移，随之位移减小到0.10，在形变大于15.71%时趋于恒定.在形变小于12.98%时，Cu1未在方向滑动，晶界结构保持了较好的对称性，在应变大于12.98%时，Cu1在在形变大于15.71%时Cu1沿该方向以拉伸的速率均匀移动.在整个拉伸和压缩过程中，Cu1始终未发生在方向的位移，因此导致方向应力在应变大于-10%时因大量积累得不到释放而增长较快.对于有B掺杂的Cu晶界，选取与清洁Cu晶界相同位置的原子进行了滑动的分析，得到了该原子在三个方向的应变-滑移曲线，如图5(e)所示.从图中可得，该原子的滑移规律与清洁Cu晶界的相似，但是由于B原子的加入，使得该原子在[130]方向产生了更大的位移，当应变为12.80%时，该方向位移为0.19，最后稳定于0.07.

3.5 电荷密度和态密度

电荷密度和态密度在分析原子成键中起到了关键作用，化学键的形成、强化、削弱等都可以由电子的积聚或耗散来描述[2].图6给出了清洁Cu晶界与有B掺杂晶界不同应变的电荷密度分布图.

清洁Cu晶界在图6(a)中给出.应变为0的电荷密度图可看出，在晶界处Cu1周围有3个电荷低密度区域，随着拉伸应变的增大，原子间距随之增大，电荷密度降低(如应变为12.98%)，使得Cu1一侧的低密度区随机的与其上下方的电荷低密度区中的一个贯通成一个较大的低密度区(应变为14.34%)，贯通过程即为晶界断裂的开始.当应变达到15.71%时，晶界上下两部分间的电荷密度为零，标志着晶界被完全拉断.在压缩过程中，随着原子间距的减小，电荷密度均匀增大.应变为-17.07%时，该Cu周围仅有一个很小的电荷低密度区.从压缩到拉伸至断裂前，Cu4与Cu6始终处于最低电荷密度区的两侧，这使得两者之间的作用很弱，较容易发生形变，这与前文键长变化相对应.

有B掺杂Cu晶界在图6(b)中给出.由于B原子掺杂到了晶界间隙位置，使得晶界处电荷得到补充，Cu1周围的低密度区变为两个.随着拉伸应变的增大，两区域逐步扩大，在应变为18.19%时达到最大.此时体系的平均间距最大，平均电荷密度最低.B与近邻的Cu原子组成一个电荷密度高于其周围的岛.在Cu1的上下、该岛的两侧各形成了一个狭长的电荷分布低密度区，当应变为19.54%时，晶界随机的从该两低密度区之一开始断裂.当应变达到20.98%时晶界中间电荷密度为零，标志着晶界完全断裂.压缩形变过程与清洁Cu晶界相似，不再赘述.

为研究B掺杂后电荷的转移情况，在图7中给出了B掺杂体系在应变为18.19%时的差分电荷密度和B的分波态密度(PDOS)图.如图7(a)，(b)所示，掺入的B仅与其周围的Cu发生显著的电荷转移，表明B的掺入仅影响晶界附近的原子，可见本文所选模型的尺寸较为合理.从图7(a)中可以看出，电子从B周围的Cu向B原子积聚，与Cu与B的电负性相对应(Cu：1.90;B：2.04).这使得Cu-B近邻Cu原子间的电荷密度降低，结合强度相对减弱.B原子的方向产生了电子的耗散.对于孤立的B原子，只有一个2p电子，以相同的概率占据p轨道的三个分量.当B掺杂到间隙位置后，B的pz与py轨道与近邻的Cu原子产生杂化而能量降低，而px轨道未参与任何作用，从而使得电荷从px轨道向能量更低的py，pz轨道转移.这与图7(c)中B的PDOS分布所反映的结论相同：在费米能级上方px空态数多于py，pz，而在费米能级下方，px出现状态数减少的同时py，pz状态数增大.另外从图7(a)还可得到，B-Cu1，B-Cu5，B-Cu7间的共价键导致了有B掺杂晶界在形变过程中B原子沿{130}方向的滑移.

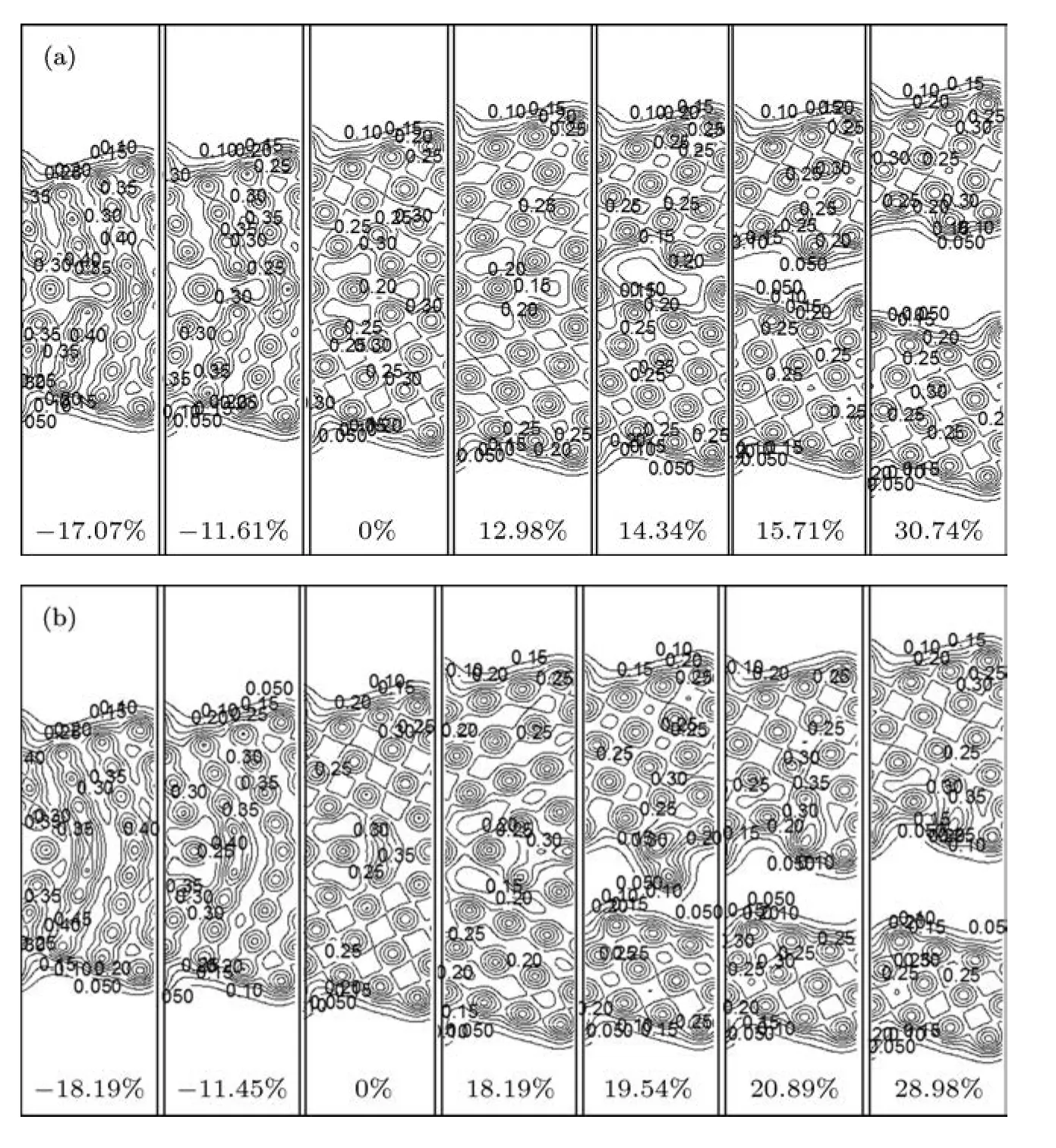
图6 (a)与(b)分别表示清洁Cu晶界与有B掺杂Cu晶界形变过程中相邻[001]面间的电荷密度分布随应变变化图(相应应变在图中给出.等高线的间隔为0.05 e/a.u.3)

图7 (a)与(b)分别表示从[001]与[130]方向观察有B掺杂Cu晶界应变为18.19%的差分电荷密度图(其中虚线表示电子耗散，实线表示电子积聚);(c)B掺杂Cu晶界应变为18.19%时B的p轨道各分量的态密度图(图中虚线为费米能级)

图8 B掺杂Cu晶界中B与近邻Cu在不同应变时的分波态密度图.(a)，(b)，(c)分别对应的应变为-18.19%，0%，18.19%(图中Ef为费米能级)

图8给出了压缩与拉伸过程中B与近邻Cu原子的PDOS，仔细分析后可得如下共同特征：

1)B与近邻Cu原子间是以B的p轨道与Cu的pd杂化轨道形成的共价键.

2)随着拉伸的进行，Cu的p轨道在pd杂化轨道中的比重越来越小;而在压缩过程中却越来越大.这可能是由于Cu的p轨道半径较小造成的.

3)拉伸过程中，体系能量整体上移，且Cu的d轨道宽度在变窄，意味着该轨道定域性增强，与B的共价键作用减弱.压缩过程与之恰好相反.

4)随着应变的增大，位于费米能级上方的B的p轨道空态数增多，这表明B的p轨道电子一方面由于与Cu的pd轨道的杂化而变得能量更低，另一方面有部分电子通过Cu-B间的共价键向Cu的pd杂化轨道，特别是d轨道反馈电子.

最后，B与Cu的p轨道电子数较Cu的d轨道少许多，应变增大导致的晶胞体积增大、平均电荷密度降低也是该两轨道状态数明显变化的一个原因.

4 结论

本文采用第一性原理方法研究了清洁Cu晶界与有B掺杂到间隙位的Cu晶界.结果表明，由B-p与Cu-pd杂化轨道形成的共价键加强了晶界的结合，理论韧性、理论拉伸强度、临界应变等分别提高46.03%，16.61%，40.00%.电荷密度和态密度分析表明，清洁Cu晶界因有间隙而电子密度较低，晶界结合能力较弱.有B掺杂的Cu晶界电子从B近邻的Cu向Cu-B间积聚，晶界结合能力得到加强，由于B-Cu间的共价键强于近邻Cu-Cu间的金属键，导致晶界拉伸开始断裂的位置由清洁Cu晶界的晶界处变为有B的掺入后的晶界近邻原子层.在形变小于20%的压缩过程中B的掺入对晶界未产生显著影响.

[2]Zhang S J，KontsevoiO Y，Freeman A J，Olson G B 2010 Phys.Rev.B 82 224107

[3]Tian Z X，Yan J X，XiaoW，Geng W T 2009 Phys.Rev.B 79 144114

[4]Yang R，Wang Y M，Ye H Q，Wang C Y 2001 J.Phys.：Condens.Matter 13 4485

[5]Wang R Z，Xu L C，Yan H，Kohyama M 2012 Acta Phys.Sin.61 026801(in Chinese)[王如志，徐利春，严辉，香山正宪2012物理学报61 026801]

[6]LozovoiA Y，Paxton A T 2008 Phys.Rev.B 77 165413

[7]Ogata S，LiJ，Yip S 2002 Science 298 807

[8]Lu L，Chen X，Huang X，Lu K 2009 Science 323 607

[9]Geng W T，Freeman A J，Wu R，Olson G B 2000 Phys.Rev.B 62 6208

[10]Geng W T，Freeman A J，Olson G B 2001 Phys.Rev.B 32 165415

[11]Schweinfest R，Paxton A T，Finns M W 2004 Nature 432 1008

[12]Geng W T，Freeman A J，Olson G B 2006 Materials Transactions 47 2113

[13]Wu R，Freeman A J，Olson G B 1994 Science 265 376

[14]Geng W T，Freeman A J，Wu R，Geller C B，Raynolds J E 1999 Phys.Rev.B 60 7149

[15]Rice J R，Wang J S 1989 Mater.Sci.Eng.A 107 23

[16]Ittermann B，Ackermann H，Stockmann H J，Ergezinger K H，Heemeier M，KrollF，MaiF，Marbach K，Peters D，Sulzer G 1996 Phys.Rev.Lett.77 4784

[17]Stockmann H J，Ergezinger K H，Fullgerbe M，Ittermann B，KrollF，Peters D 2001 Phys.Rev.B 64 224301

[18]Yuasa M，MabuchiM 2010 J.Phys.：Condens.Matt.22 505705

[19]Yuasa M，MabuchiM 2010 Phys.Rev.B 82 094108

[20]Zhang Y，Lu G H，Kohyama M，Wang T M 2009 Modelling Simul.Mater.Sci.Eng.17 015003

[21]Zhang L，Shu X L，Jin S，Zhang Y，Lu G H 2010 J.Phys.：Condens.Matt.22 375401

[22]Janisch R，Ahmed N，Hartmaier A 2010 Phys.Rev.B 81 184108

[23]YamaguchiM，Nishiyama Y，KaburakiH 2007 Phys.Rev.B 76 035418

[24]Kronberg M L，Wilson F H 1949 Trans.Am.Inst.Min.Metall.Pet.Eng.185 501

[25]Sørensen M R，Mishin Y，Voter A F 2000 Phys.Rev.B 62 3658

[26]Duscher G，Chisholm M F，Alber U，Rhle M 2004 Nat.Mater.3 621

[27]YamaguchiM，Shiga M，KaburakiH 2005 Science 307 393

[28]Chen Z Z，Wang C Y 2005 J.Phys.：Condens.Matter 17 6645

[29]Kresse G，Hafner J 1993 Phys.Rev.B 47 558

[31]Perdew J P，Burke K，Ernzerhof M 1996 Phys.Rev.Lett.77 3865

[32]ZhaoY，Truhlar D G 2004 J.Phys.Chem.A 108 6908

[33]Wong B M 2009 J.Comput.Chem.30 51

[34]LozovoiA Y，Paxton A T，Finns M W 2006 Phys.Rev.B 74 155416

[35]Kittel1996 Introduction tosolid state physics(New York：John Wiley and Sons Inc.)

[36]Tyson W R，Miller W A 1977 Surf.Sci62 267

[37]Cheng Y，Jin Z H，Zhang Y W，GaoH 2010 Acta.Mater.58 2293

[39]BalloP，Slugen V 2005 Comp.Mater.Sci.33 491

[41]Lu G H，Deng S H，Wang T M，Kohyama M，YamamotoR 2004 Phys.Rev.B 69 134106