Cluster与Corona乘积图的hyper-Wiener指标

罗朝阳孙德荣蔡 华

（1，2，3.昌吉学院数学系 新疆 昌吉 831100）

Cluster与Corona乘积图的hyper-Wiener指标

罗朝阳1孙德荣2蔡 华3

（1，2，3.昌吉学院数学系 新疆 昌吉 831100）

分别给出了两个连通图G和H的Cluster与Corona乘积G{H}和G。H的hyper-Wiener指标的精确表达式及其应用例子.

Hyper-Wiener指标,Cluster乘积,Corona乘积,连通图

1 引言

分子结构描述符Top又称分子拓扑指标．它是一个与化学分子图相关的实常数且不依赖于该分子图的标记和结构性特征表示.迄今为止，大量的分子拓扑指标，如第一、二类Zagreb指标M1和M2，Wiener指标W，hyper-Wiener指标WW，Randic'指标R，Hosoya指标Z，Szeged指标Sz和点、边PI指标PIv和PIe以及它们的改进版和变体等，已经在许多化学类研究文献中被定义，这些拓扑指标的许多数学性质也在数学类文献中被研究。同时发现那些基于图中点度和距离的拓扑指标在物理化学建模、药理学、毒理学、生物学和纳米材料学、化合物的其它性质的研究以及QSPR和QSAR分析中分子螺旋形态的表征等方面都有重要的应用．

1947年,美国化学家Wiener［1］为了研究石蜡的沸点，提出了基于图中距离的拓扑指标—Wiener指标，该指标之后便得到广泛地关注和研究。连通图G的Wiener指标被定义为G中所有无序点对之间距离的和.研究显示该指标与分子的物理化学性质具有高相关性．关于Wiener指标的更多研究结果与应用,见文献［2–8］.无圈图的hyper-Wiener指标首先是由Milan Randic'在1993年提出的,之后Klein［9］等人将此定义推广到所有连通图.Khalifeh等人［10］计算了图的笛卡尔乘积，复合，连图和不交并的hyper-Wiener指标.Metsidik等人［11］确定了F-sum图的hyper-Wiener指标.Eliasi和Iranmanesh［12］计算了广义层积图的hyper-Wiener指标.关于hyper-Wiener指标的若干化学应用和数学性质见文献［13–18］.

近十年间,由于大分子合成的需要以及超大型复杂网络的出现,对于合成图的研究屡见不鲜.特别是乘积图（笛卡尔积、克罗内克积、Cluster积、Corona积、层积及广义层积等）,复合图,连图,图的对称差、不交并等的相应拓扑指标的研究成果居多.Yeh和Gutman计算了一些合成图的Wiener指标.Sagan等人［19］及Stevanovic'［20］确定了一些合成图的Hosoya多项式.张和平等人［21］计算了连图，Cluster乘积图和Corona乘积图的Kirchhoff指标.本文给出了连通图G和H的Cluster乘积和Corona乘积G{H}和G∘H的hyper-Wiener指标的精确表达式，同时利用所得结果计算了一些特殊图类的Cluster和Corona乘积图的hyper-Wiener指标.

2 预备知识

文中涉及的图均为有限的无向简单连通图,未定义的术语与符号见文［22］.设连通图G的点、边集分别为V（G）和E（G）,它们的基数记为|G|和|E（G）|.图G中点v的度及点v的邻点集合分别记为dG(v)和

NG(v),则dG(v)=|NG(v)|.图G中任意两点u和v之间的距离dG(u,v)表示u和v间的一条最短路的边数.令d(u,G)=∑v∈V(G)dG(u,v)且d'(u,G)=∑v∈V(G)(dG(u,v))2.对于图G和H，若存在双射θ:V（G）→V（H）与φ:E（G）→E（H），使得ΨG(e)=uv当且仅当ΨG(φ(e))=θ(u)θ(v)，则称G和H同构,记为G≅H.一般地,若G≅H,则Top（G）=Top（H）.

连通图G的Wiener指标W(G)和hyper-Wiener指标WW(G)分别定义如下：

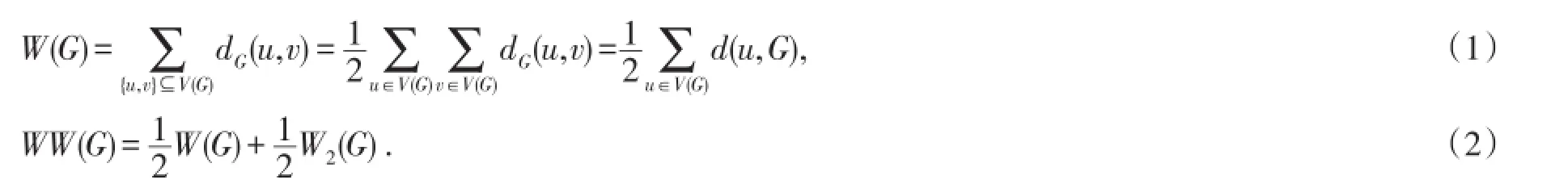
一个根图是指选定它的一个点作为根点，以区别于其余点.本文主要涉及的几种合成图为：Cluster乘积图，Corona乘积图和连图［8］.

连通图G和H（根图）的Cluster乘积记为G{H}，由G的一个拷贝和根图H的|G|个拷贝构成，是将H的第i个拷贝的根点与G的第i个点相连，i=1,2,···,|G|.

连通图G和任意一个图H的Corona乘积记为G∘H，由G的一个拷贝和H的|G|个拷贝构成，是将H的第i个拷贝的每一个点都与G的第i个点相连，i=1,2,···,|G|.

图G和H连图G+H：V（G+H）=V（G）∪V（H）；E（G+H）=E（G）∪E（H）∪{（u,v）|u∈V（G）,v∈V（H）}.

关于两个图的Cluster与Corona乘积的Wiener指标，有如下已知结果：

定理1.［8］设G和H为连通图,x是图H的根点，则

定理2.［8］设G为连通图，则对于任意图H，有

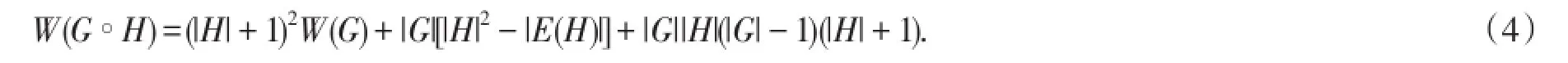
3 Cluter乘积图的hyper-Wiener指标

设G和H为两个连通图,Hi（i=1,2,···,|G|）是H的第i个拷贝.简便起见，记u∈V(Hi)为u∈Hi.下面给出Cluster乘积图G{H}的hyper-Wiener指标的计算表达式.

定理3.设图G和H连通，x是H的根点,则

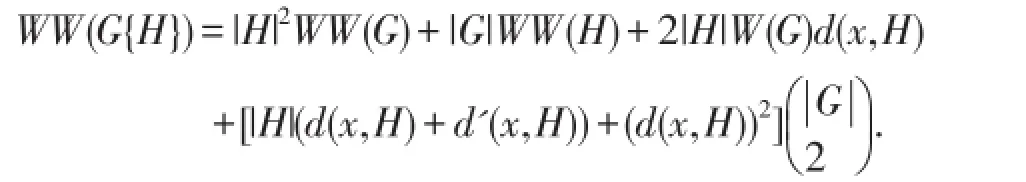
证明.先求W2（G{H}）.若G{H}的点u和v均属于H的同一拷贝,则dG{H}(u,v)=dH(u,v).这些点对给W2（G{H}）的贡献为=|G|W2（H）.若G{H}的点u和v分别属于H的不同拷贝，则dG{H}(u,v)=dH(u,xi)+dG(xi,xj)+dH(xj,v)，其中xi和xj分别是G的被H的根点粘附的两个点.i,j∈{1,2,…, |G|}且i≠j.这些点对给W2（G{H}）的总贡献为

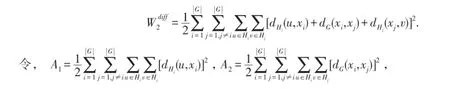
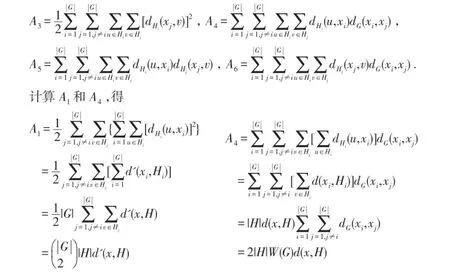
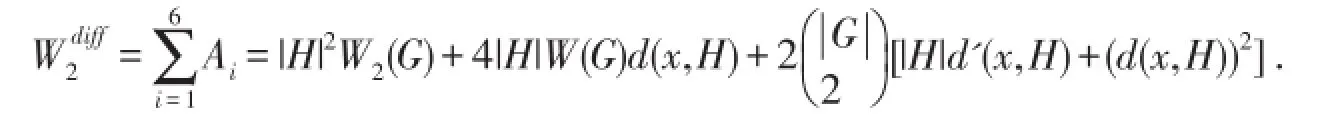
对以上两类G{H}的无序点对u,v的贡献求和，得

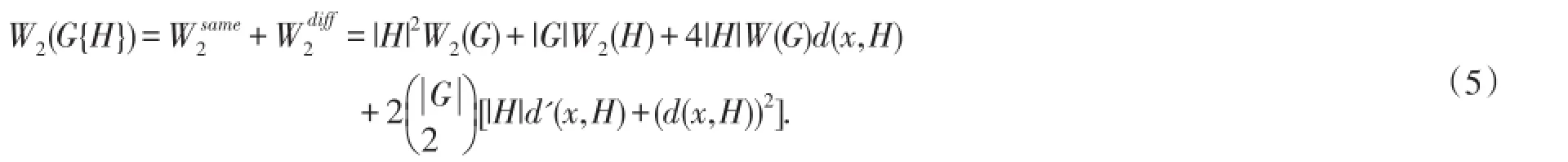
根据hyper-Wiener指标的定义，由等式（3）和（5）可得,

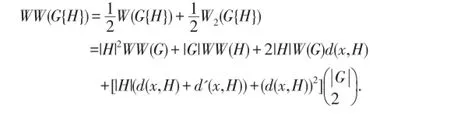
证毕.

引理1.［10,19］设Kn、Pn和Cn分别表示n阶完全图、路和圈,其中x为它们的根点.Kn与Cn中点x任选，Pn中点x取其一个悬挂点.则

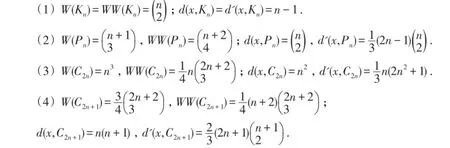
例1.设m,n为正整数且m≥2,n≥2.令x为Kn与Pn的根点.Kn中x任选，Pn中x为其一个悬挂点.则由定理3和引理1,可得

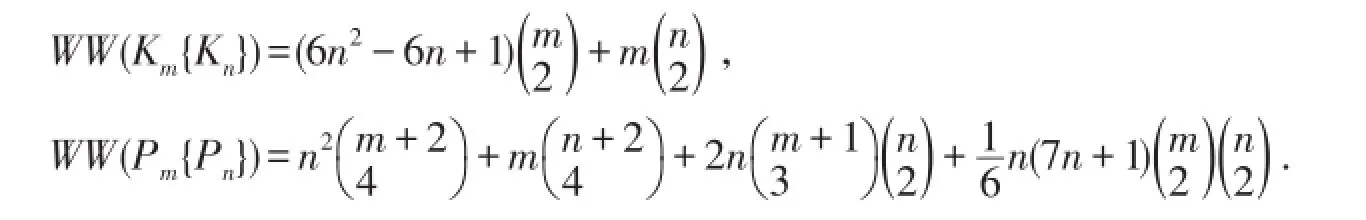
同理可计算Pm{Ck}，Cm{Ck}和Ck{Pn}（k=2n,2n+1）等Cluster乘积图的hyper-Wiener指标.由于计算方法类似，故此处略去相应的表达式.

4 Corona乘积图的hyper-Wiener指标

下面计算G和H的Corona乘积G。H的hyper-Wiener指标.关于任意两个图的连图的hyper-Wiener指标，有以下已知结果：

定理4.［10］对于任意两个图G和H，有

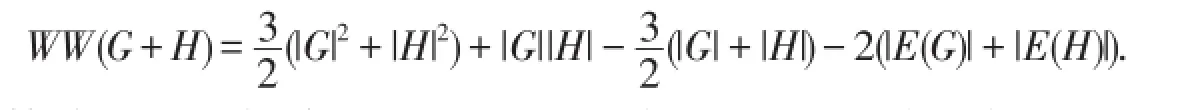
由于两个图join运算满足交换律，令G≅K1，x为K1中的唯一孤立点，则H+x≅H+K1.故引理2是定理4的直接结果.

引理2.对于图H和任意一个孤立点x，有

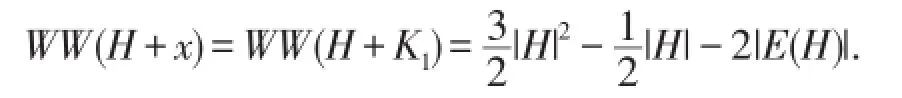
定理5.设图G连通,则对于任意图H,有

证明.令x为图H+x的根点.因为G∘H≅G{H+x}，于是由定理3和引理2，定理5得证.

例2.设m,n为正整数且m≥2，n≥2.则由引理1和定理5，得

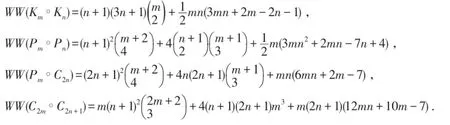
类似地，可计算Pm∘C2n+1，C2m∘C2n，C2m+1∘C2n+1及C2m+1∘C2n等的hyper-Wiener指标，此处略去。

［1］Wiener H.Structural determination of paraffin boiling points［J］.Journal of the American Chemical Society,1947,69:17-20.

［2］Gutman I,Polansky O E.Mathematical Concepts in Organic Chemistry［M］.Berlin:Springer, 1986.

［3］Dobrynin A A,Entringer R,Gutman I.Wiener index of trees:Theory and applications［J］.Acta Appl.Math.,2001,66:211-249.

［4］Dobrynin A A,Gutman I,Klavžar S,ZigertP.Wiener index of hexagonal systems［J］.Acta Appl. Math.,2002,72:247-294.

［5］Gutman I,Klavoar S,Mohar B.（Eds.）Fifty years of the Wiener index［J］.MATCH Commun. Math.Comput.,1997,35:1259.

［6］Graovac A,Pisanski T.On the Wiener index of a graph［J］.J.Math.Chem.,1991,8:53-62.

［7］Klavžar S,Gutman I.Wiener number of vertex-weighted graphs and a chemical application［J］. Discrete Appl.Math.,1997,80:73-81.

［8］Yeh Y N,Gutman I.On the sum of all distances in composite graphs［J］.Discrete Math.,1994, 135:359-365.

［9］Klein D J,Lukovits I,Gutman I.On the definition of the hyper-Wiener index for cyclecontaining structures［J］.J.Chem.Inf.Comput.Sci.,1995,35:50-52.

［10］Khalifeh M H,Yousefi-Azari H,Ashrafi A R.The hyper-Wiener index of graph operations［J］. Comput.Math.Appl.,2008,56:1402-1407.

［11］Metsidik M,Zhang W,Duan F.Hyper-and reverse-Wiener indices of F-sums of graphs［J］.Discrete Appl.Math.,2010,158:1433-1440.

［12］Eliasi M,Iranmanesh A.The hyper-Wiener index of the generalized hierarchical product of graphs［J］.Discrete Appl.Math.,2011,159:866-871.

［13］Cash G G.Relationship between Hosaya polynomial and the hyper-Wiener index［J］.Appl. Math.Lett.,2002,15:893-895.

［14］Cash G G.Polynomial expressions for the hyper-Wiener index of extended hydrocarbon networks［J］.Comput.Chem.,2001,25:577-582.

［15］Gutman I.Relation between hyper-Wiener and Wiener index［J］.Chem.Phys.Lett.,2002,364: 352-356.

［16］Klavžar S,Gutman I.A theorem on Wiener-type invariants for isometric subgraphs of hypercubes［J］.Appl.Math.Lett.,2006,19:1129-1133.

［17］Klavžar S,Zigert P,Gutman I.Analgorithm for the calculation of the hyper-Wiener index of benzenoid hydrocarbons［J］.Comput.Chem.,2000,24:229-233.

［18］Pattabiraman K,Paulraja P.On some topological indices of the tensor products of graphs［J］.Discrete Appl.Math.,2012,160:267-279.

［19］Sagan B Y,Yeh Y N,Zhang P.The wiener polynomial of a graph［J］.Int.J.Quantum Chem., 1996,60:959-969.

［20］Stevanovi[c']D.Hosoya polynomial of composite graphs［J］.Discrete Math.,2001,235（1）:237-244.

［21］Zhang H P,Yang Y J,Li C W.Kirchhoff index of composite graphs［J］.Discrete Appl.Math., 2009,157:2918-2927.

［22］West D B.Introduction to Graph Theory,second ed［M］.NJ:Prentice-Hall,Upper Saddle River,2001.

O157.5,O157.6

：A

：1671-6469（2013）04-0072-05

2013-07-03

昌吉学院科研基金项目（2012YJYB003）

罗朝阳（1969-），男，陕西礼泉人，昌吉学院数学系，副教授，研究方向：复杂网络，图论及其应用。