百慕大期权定价方法及实证研究

刘福国

（昌吉学院数学系 新疆 昌吉 831100）

百慕大期权定价方法及实证研究

刘福国

（昌吉学院数学系 新疆 昌吉 831100）

利用保险精算方法给出连续市场模型下百慕大期权定价公式，并对我国的上海权证市场中的百慕大式权证的实际数据利用离散（二叉数方法）和连续市场（保险精算方法）两种模型下的百慕大期权定价公式进行实证分析。

百慕大期权;保险精算定价;二叉树;实证分析

1 引言

期权按照交易时间的不同，期权有欧式期权和美式期权之分，标准美式期权可在其有效期内任何时间均可行使期权，标准欧式期权只能在约定时间行使权力，因而美式期权比欧式期权应用得更为普遍，国际金融衍生市场交易的大多数期权都是美式期权，但实际中交易的美式期权不一定总是具备这些标准特征，尤以股票期权市场最为突出，例如百慕大（bermudan）期权,就只限于在期权有效期内特定日期而不是在任何时间可行使期权，即其价格具备路径依赖特征，例如一些公司发行的某些认购权证和认沽权证。可见百慕大期权的定价既有重要的理论价值，又具有重要的现实意义，因而百慕大期权的定价一直是国内外众多学者研究的热点之一。但是由于路径依赖特征的复杂性，百慕大期权的定价相对较难，关于该问题研究的文献比较少，如2005年林建伟采用偏微分方程方法讨论了带跳扩散项的永久百慕大期权定价问题［1］，但他仅解决作为周期解的连续的数学模型，但没有给出一般连续市场模型下百慕大期权定价公式。

保险精算定价法最早由Bladt M和Rydberg HT应用到期权定价中［2］，闫海峰，刘三阳［3］利用保险精算法推广了B-S模型，推导出了股票价格遵从Ornstein-Uhlenback过程的期权定价;随后众多国内外学者将此方法进一步推广，如刘倩、刘新平［4］和叶小青［5］把保险精算法推广到外汇期权、亚式期权的定价问题中等等，由于保险精算法模型无任何条件假设的优越性使该方法的应用极具推广性。本文利用保险精算方法给出连续市场模型下百慕大期权定价公式并给出相应的实证分析。

2 百慕大期权定价方法

定义2.1［6］按和约规定，提前实施只限于期权有效期内的一些特定时间才可以进行，在其他时间与其它欧式期权一样不能提前实施,此类期权称之为百慕大期权。

2.1 二叉树模型

二叉树模型首先解决的就是股价走势的问题，虽然不知道未来某个时点的股价具体是多少，但是二叉树模型认为在较短的时间间隔内，股票价格S只有两种运动方向，以概率p向上增长为Su，或以概率1-p下降为Sd，根据股价的历史波动率，可推算u,d并设定如下：

在给期权定价时，实务界一般认为采用20步二叉树就能取得较好的定价效果，并且我们通过适当调整步长使行权点刚好与二叉树分层点重合，对于看跌期权而言，由于最后一层节点处为期末，期权的价值仅为立即行权的价值max{X-ST,0}，然后根据公式（2.2）不断的往前回溯，如果该节点处有行权的权利，则期权价值为：

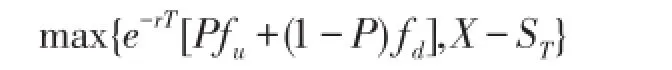
如果该节点处无行权的权利，则期权价值为：e-rT[Pfu+(1-P)fd]，回溯到第一个节点时则为百慕大期权价值

其中P=。

2.2 连续模型

我们考虑由两类资产（证券）组成的连续贸易金融市场,一种是在t时刻具有瞬时无风险利率为r(t)的无风险资产Q(t)（如债券）;另一类为风险资产（如股票）,在t时刻其价格为S(t),考虑的时间区间为[0,T],0表示为初始时间,T表示为到期日,{S(t):t≥0}是定义在给定的滤子化完备概率空间(Q,F,F(t)t≥0,P)上的随机过程,{F(t):t≥0}是由S(t)产生的自然滤子,假设S(0)=S是大于零的常数（有关保险精算定价的的概念沿袭文献［2］［3］）。

假设风险资产（股票）的价格过程{S(t):t≥0}和无风险资产的价格过程{Q(t):t≥0}分别满足:

其中Bt表示定义在完备概率空间(Ω,F,P)上的标准Brown运动。S(0)=S,S是大于零的常数,r(t),μ(t),σ(t)是[0,∞]→R上的函数,且满足

设C(X,T)和P(X,T)分别表示以股票价格S(t)为标的资产,执行价为X,到期日为T的百慕大式看涨和看跌期权的保险精算定价。

对于标的资产不支付中间红利的百慕大期权定价有如下结论：

定理2.1假设{S(t):t≥0},{Q(t):t≥0}满足方程（2.3）、（2.4）且风险资产在有效期内无红利支付,则百慕大期权保险定价公式是：

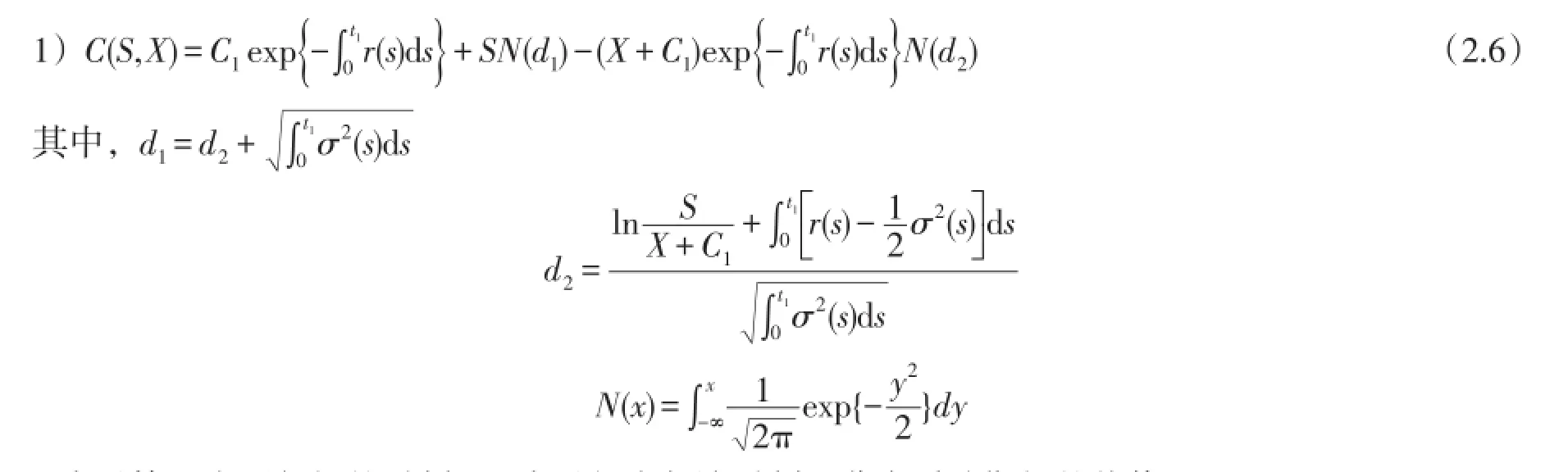
t1表示第一个可行权的时刻，C1表示相应与该时刻百慕大看涨期权的价值。

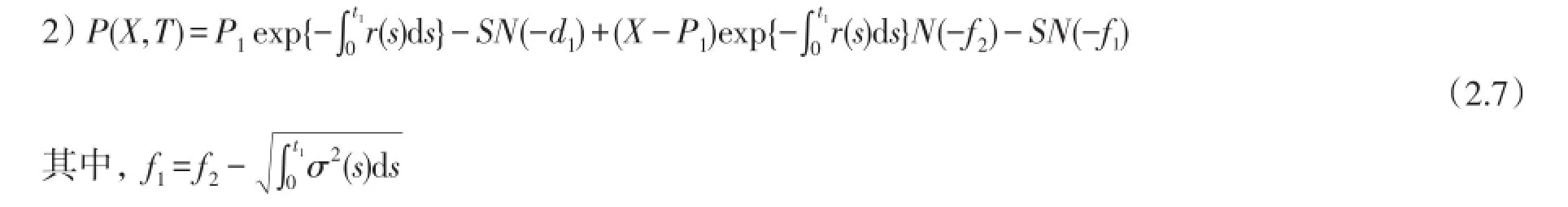
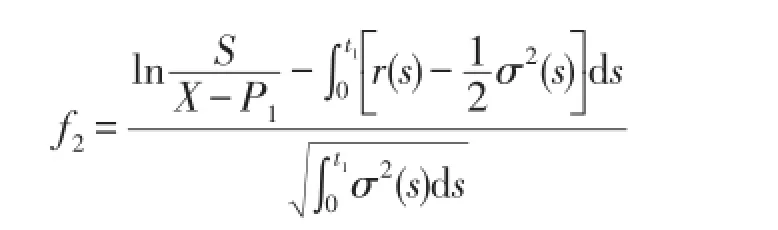
t1表示第一个可行权的时刻，P1表示相应与该时刻百慕大看跌期权的价值。

证明：由伊藤引理，随机微分方程（2.3）有唯一解

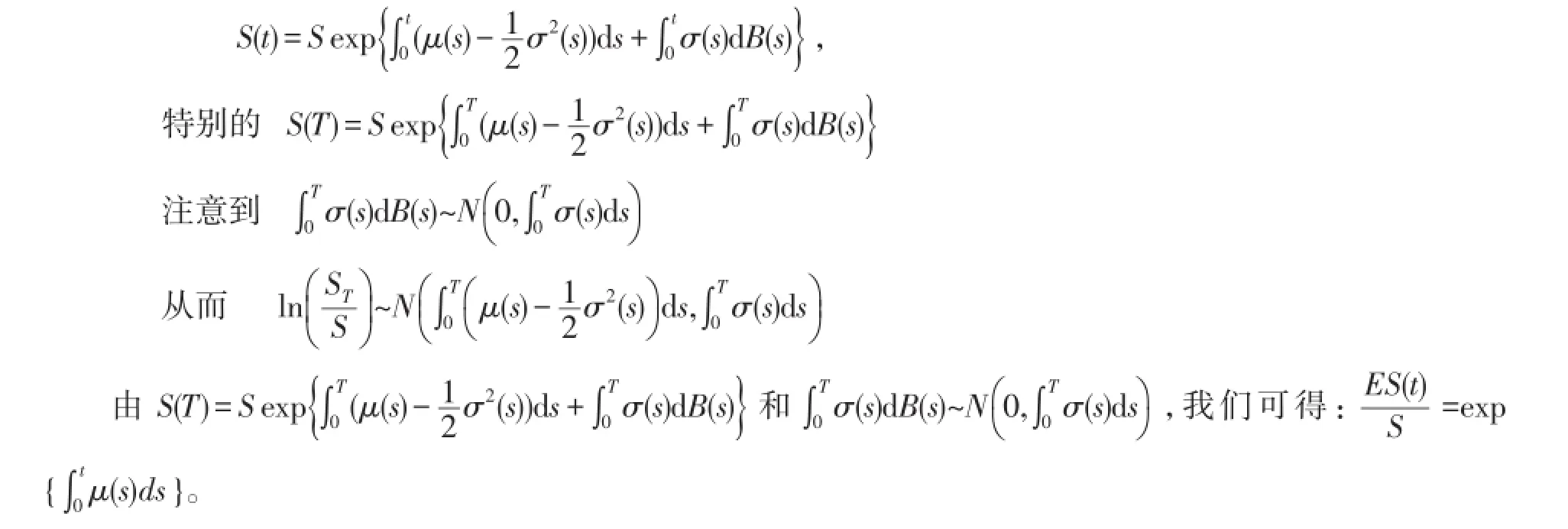
（Ⅰ）先对1)式进行证明

设t1,t2,……,tN为可以行权的时刻，把[0,T]分为：0≤t1≤……≤tN=T,实际中不同期权N不同。

当N=2时,即0＜t1＜T在[0,T]内只有t1，T时刻才可以行权；

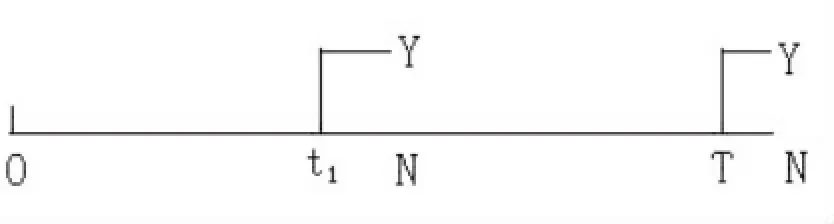
图中Y表示执行期权，N表示不执行期权

如上图所示，在t1时刻或执行或不执行，如果：

(a)t1时刻不执行，则此期权为在[t1,T]上的欧式期权，在t1时刻的价值为C1(X,T-t1)，则：

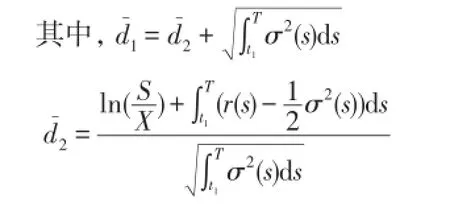
(b)t1时刻若执行，其执行条件为：S(t1)-X＞C1⇔S(t1)＞C1+X

按保险精算法其执行条件应为：

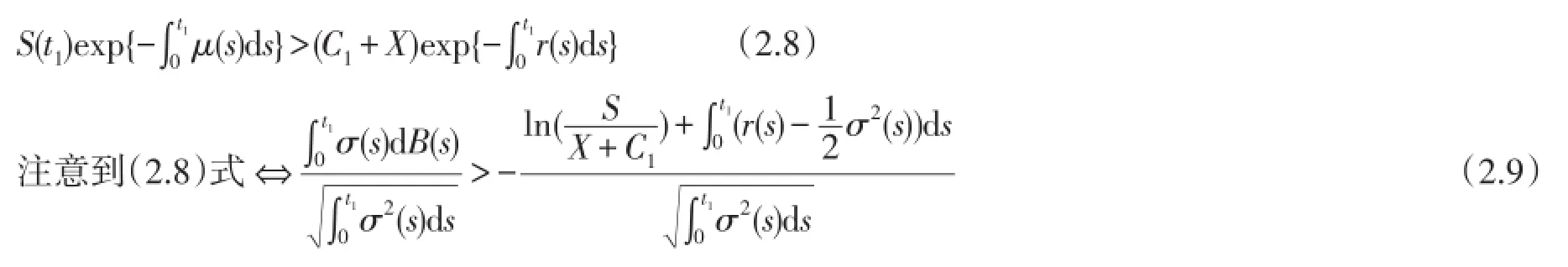
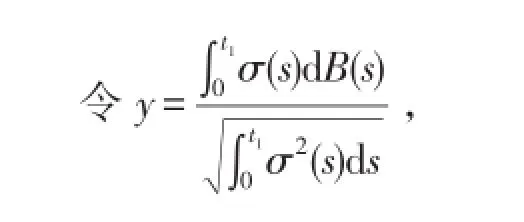
那么综合（a）（b），有：

由于（2.10）式中：

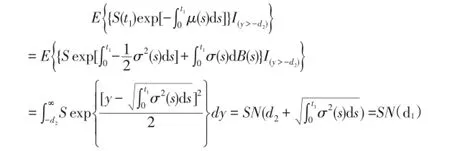
当N＞2时,即t1,t2,……,tN为可以行权的时刻，把[0,T]分为：0≤t1≤……≤tN=T。

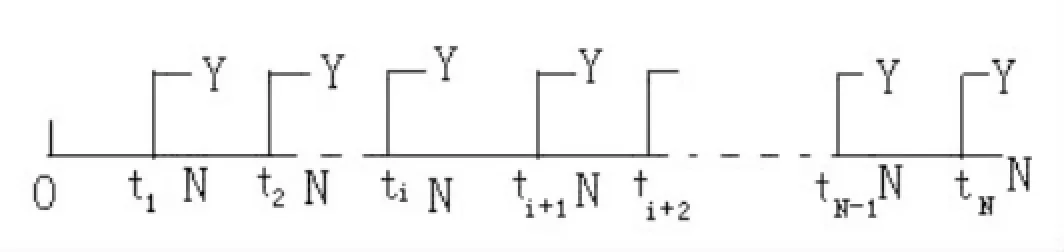
图中Y表示执行期权，N表示不执行期权

同1∘中理：

(a)当tN-1时刻不执行，则此期权为在[tN-1,T]上的欧式期权，在tN-1时刻的价值为CN-1(X,T-tN-1),则：

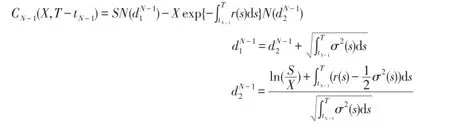
(b)当tN-1时刻若执行，按保险精算法可推得tN-1时刻百慕大期权的价值为：CN-2(X,T-tN-2)

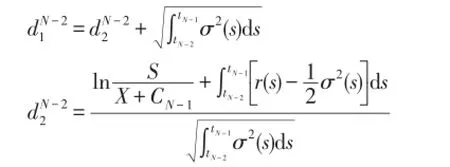
如上依次往前递推，最终可得出0时刻百慕大看涨期权的价值即为结论1)，即：得证。

同(1)式理可证明(2)式。证明完毕。

对于百慕大期权的定价其它定价法相比较，保险精算定价模型具有以下特点：

一、没有对金融市场和价格过程作任何限制，计算期权价格时只利用了价格过程在期末时的实际概率分布和公平保费原理,克服了鞅方法定价中寻找等价鞅测度的困难，并且克服了其他模型难求显式解的困难。

二、与传统的无套利定价有许多本质的区别:保险精算定价中买权执行条件为而不是S(t1)＞C1+X与期权定价的鞅方法相比较，保险精算方法的不同之处在于：计算数学期望所用的概率测度、期权被执行的条件以及计算可能损失的方式。当金融市场是有套利、非均衡（等价鞅测度不存在）或不完备（等价鞅测度存在但不唯一）鞅方法将不能使用。保险精算方法将期权定价问题转化为等价的公平保费确定问题，由于无任何经济假设，所以它不仅对无套利、均衡、完备的市场有效，且对有套利、非均衡、不完备的市场也有效。

3 实证研究

定义3.1权证［7］，是指标的证券发行人或其以外的第三人发行的，约定持有人在规定期间内或特定到期日，有权按约定价格向发行人购买或出售标的证券，或以现金结算方式收取结算差价的有价证券。

权证本质上是期权的一种，百慕大式权证实质就属于百慕大期权，在我国的权证市场中大部分的权证是百慕大式的，百慕大权证吸收了欧式权证和美式权证的灵活性，更加满足市场的需求，对其定价就显得更加重要。本文对中国上海权证市场中2006年以来的所有百慕大式认沽权证和认购权证（合计22种权证）的自发行以来每天的收盘价格作为实际数据，并以MATHLAB作为数学模拟工具对二叉树模型和保险精算方法分别进行模拟，并与实际进行比较，部分结果如下图：

通过实证分析我们有如下结论：

首先，我们可以从实证图形结果很直观的看出保险精算方法为百慕大权证定价较目前使用的二叉树方法更接近实际，更能反映实际的市场变化趋势；对所有的百慕大式认沽权证和认购权证都使用该方法进行分析，其结果说明保险精算定价结果比二叉树定价结果更接近实际,并且对其中所有数据统计得（总天数为250）:保险精算结果优于二叉树结果的天数为150的占100%,为180的占92%,为220的占62%,为240的占52%。

其次，我们为了比较保险精算方法和二叉树方法对于百慕大期权定价与实际谁更接近，采用假设检验的方法［8］进行验证：

对于二叉树、保险精算每天定价的对数值与实际价格的对数值的差是成对的，即有n对相互独立的计算结果(α1,β1),(α2,β2),……,(αn,βn),令D1=α1-β1,D2=α2-β2,……,Dn=αn-βn,则D1,D2,……,Dn相互独立。假设Di～N(μD,),i=1,2,……,n，

这就是说D1,D2,……,Dn构成正态总体N(μD,)的一个样本，其中μD,未知。我们需要基于这一样本检验假设：H0≥0,H1≤0 （1）

分别记D1,D2,……,Dn的样本均值和样本方差的观察值为ˉ,，那么关于单个正态总体均值的t检验知检验问题（1）的拒绝域为（检验水平为α=0.05）：，由求出t值判断是否落在拒绝域内来判断接受H0或H1，接受H0即说明保险精算数据比二叉树数据更接近实际数据。

例如包钢认购权证：D1,D2,……,Dn的样本均值ˉ=0.2281，样本方差的观察值为SD=0.3740，现在,即知问题（1）的拒绝域为：

即接受H0，说明包钢认购权证的保险精算定价结果比二叉树定价结果更接近实际。

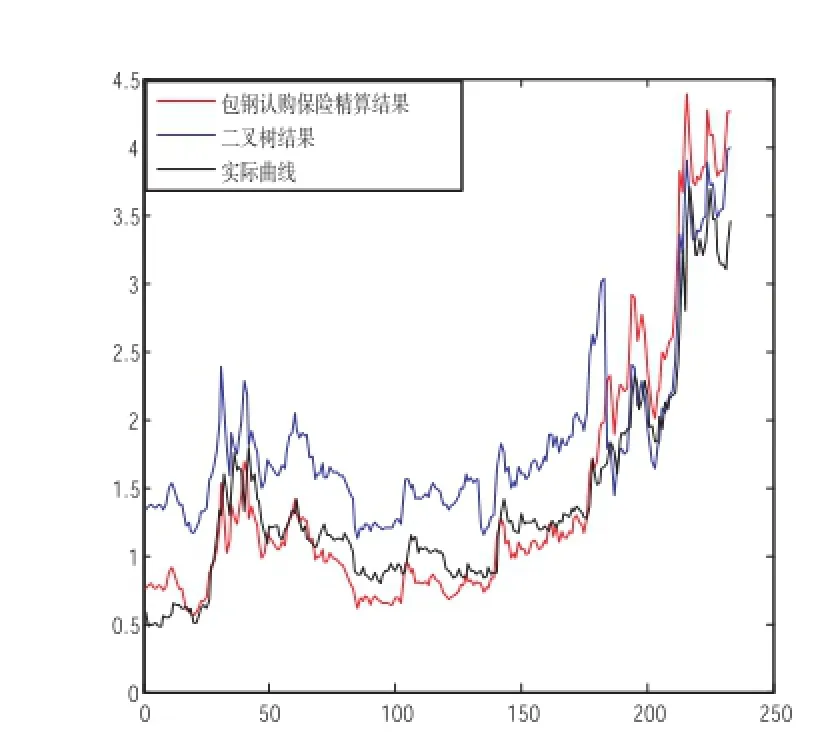
邯钢认购权证定价比较示意图

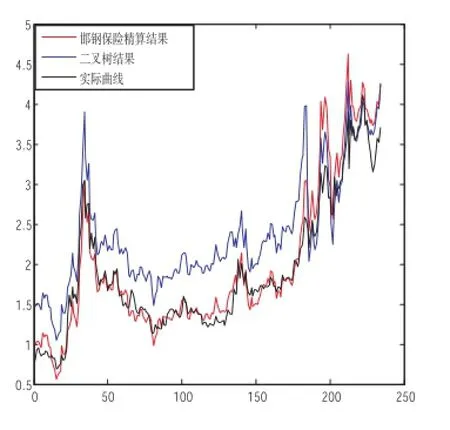
包钢认购权证定价比较示意图

最后，保险精算定价模型的条件假设更为自由，更贴近实际，将期权定价问题转化为等价的公平保费确定问题,由于无任何经济假设,所以它不仅对无套利、均衡、完备的市场有效,且对有套利、非均衡、不完备的市场也有效。但权证是指标的证券发行人或其以外的第三人发行的，反映的是发行人与持有人之间的一种契约关系，发行人也以追求经济利益为目的，而且权证的价格往往还要受到权证的市场供求、发行人业绩等因素影响，所以造成对于百慕大式认沽权证和认购权证的理论价值有时与实际价格存在一定的差距。

本文对于百慕大期权定价是在标的资产不存在分红和利率、波动率是时间t的连续函数的假设条件下进行的，标的资产存在分红和利率、波动率是随机情形还有待继续研究。

［1］林建伟.带跳扩散项的永久百慕大期权定价［J］.莆田学院学报,2005,（4）.

［2］Bladt M,Rydberg H T.An actuarial approach to option pricing under the physical measure and without market assumpions［J］.Insurance:Mathematics and conomics,1998,22（1）:65-73.

［3］闫海峰，刘三阳.广义Black-Scholes模型期权定价方法——保险精算方法［J］.应用数学与力学，2003,7（7）：730-737.

［4］刘倩,刘新平.外汇期权定价的新方法—保险精算方法［J］.贵州大学学报，2004,（2）.

［5］叶小青，吴永红.亚式期权的保险精算定价［J］.华中科技大学学报,2005,（3）.

［6］［美］John C.Hull.期权,期货和其它衍生产品［M］.华夏出版社,2000.

［7］魏宗舒.概率论与数理统计教程［M］.高等教育出版社,1983.

［8］钱敏平,龚光鲁.随机过程论［M］.北京大学出版社,2004.

［9］姜礼尚.期权定价的数学模型和方法［M］.高等教育出版社,2002.

O212.7

：A

：1671-6469（2013）04-0042-06

2013-06-26

昌吉学院科研项目（2011SSQD02）

刘福国（1978—），男，新疆昌吉人，昌吉学院数学系，讲师，研究方向：应用数学。