步枪弹侵彻明胶靶标的数值模拟

温垚珂，徐诚，陈爱军，史晓宁

(1.南京理工大学 机械工程学院，江苏 南京210094;2.南京理工大学 理学院，江苏 南京210094)

0 引言

步枪弹终点效应涉及到侵彻过程、瞬时空腔效应和压力波效应等现象。步枪弹威力和终点效应的实验研究和评判主要采用明胶靶标或肥皂靶标进行。与肥皂靶标相比，明胶靶标的物理响应更接近生物靶标，且更容易进行终点效应的瞬时拍摄与测量，故明胶靶标在国外终点效应研究中应用更广泛。目前，世界上部分国家已制定了采用明胶靶标评判枪弹杀伤威力的实验方法与标准，但明胶靶标只能在有枪弹样弹时才能进行实验和评判，且实验评判一般准备周期长，实验成本高。近年来，随着有限元技术的快速发展，数值计算方法开始应用于枪弹终点效应的研究与评判中。数值方法可以提供更全面的数据并可以方便地再现侵彻过程，有助于更好地揭示终点效应过程和机理，极大地节约研究经费，且可以在步枪弹图纸阶段预测其终点效应和杀伤威力，指导步枪弹设计，具有广泛的应用范围与前景。

Nsiampa 等［1］借助于Autodyn-3D 软件模拟了7.62 NATO 弹头在肥皂中的翻滚情况，数值结果与理论分析结果基本吻合。Salisbury 等［2］和Kwon等［3］采用SHPB 方法研究了明胶在不同应变率下的应力应变关系，为更好地开展数值研究提供了必要支持。Datoc［4］用LS-DYNA3D 软件模拟了手枪弹侵彻长方体明胶靶标的作用过程，并对明胶采用不同材料本构时对数值结果的影响进行了分析。Koene等［5］采用实验与数值模拟相结合的方法对球形杀伤元以较低速度撞击明胶的过程进行了分析。目前，国外采用数值计算方法研究步枪弹终点效应的工作尚处于起步阶段，国内未见有文献报道。

1 数值模型及验证

1.1 数值模型

结合相关实验，建立子弹与明胶靶标作用的有限元模型。该弹头分为被甲、钢芯和铅芯3 部分(图1(a))。实验中采用的明胶靶标为边长30 cm的立方体，在子弹与明胶的直接接触区及附近划分较密的网格，网格尺寸与弹头单元尺寸相近，在与接触区域较远处采用相对较粗的网格(图1(b))。设定弹轴与入射面垂直，速度方向与弹轴夹角0.7°，入射速度833 m/s.定义子弹与明胶间采用面面侵蚀接触(ERODING_SURFACE_T0_SURFACE)算法。由于单点积分的lagrange 算法在单元大变形时会产生严重的沙漏变形，因此采用基于粘性的沙漏控制算法，设置沙漏系数为0.01.这样可以较好地抑制沙漏对数值结果可靠性的影响。

图1 有限元模型Fig.1 Finite element mesh of bullet and gelatin

1.2 弹靶材料模型

JOHNSON_COOK 材料模型适合描述材料在大变形、高应变率和高温条件下的本构关系，在弹道侵彻冲击、金属爆炸成型等数值计算中应用较广。因此采用该材料模型描述子弹的本构关系。其本构关系的表达式［6］为

式中D1～D5为材料常数。

GRUNEISEN 状态方程可通过两种方法定义压力体积的关系，从而确定材料是压缩还是扩张。该状态方程定义压缩材料的压力如下:

表1 子弹材料模型参数Tab.1 Mechanical properties of materials of bullet

对于膨胀材料的压力:

以学生为中心的教学改革是教育思维模式的颠覆性变革，“关键是将教与学的重心真正地转变到以学生为中心的教育上来，实现从以教为中心到以学为中心的转变”［1］。把这一理念落实到教学实践中并不是一件容易的事，这既涉及到教师的教学习惯，又与学生的学习习惯有关。就教学本身的目的而言，这一理念也应运用于指导成人教育。我们这里提出的“以学习者为中心”，不仅强调在教学中要以学生为中心，更要明确指出，教育教学的一切工作都要以学生为中心，真正地把提高学生的核心能力作为成人教育的中心任务。

式中:E 为材料的内能;c 为冲击波速度-质点速度Hugoniot 曲线(vs-vp曲线)的截距;S1～S3为vs-vp曲线的斜率;γ0是Gruneisen 系数;a 是γ0和μ=ρ/ρ0-1的一阶体积修正量。

明胶是一种高分子材料，在一定压力下具有流变性质，因此可以采用结合线性状态方程(LINEAR_POLYNOMIAL)下的流体弹塑性材料模型(MAT_ELASTIC_PLASTIC_HYDRO)来描述该特性［7］。该模型用于描述各向同性弹塑性材料在低压下的本构关系，采用自然应变，将应力分成偏量和流体静压予以分别考虑。应力偏量和应变偏量之间采用微分关系，且用于变形的全过程。状态方程用于描述材料在高压下的压力体积关系［8］。

该本构关系中屈服强度按下式计算:

式中σy为y 轴方向上的屈服强度。

根据弹性模量E 和切线模量Et可计算塑性硬化模量Eh:

线性状态方程的表达式为

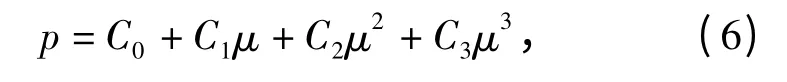
式中:p 为压力;C0～C3为材料常数;μ=ρ/ρ0-1;ρ、ρ0分别为现时密度和初始密度。明胶的状态方程参数如表2所示。

1.3 数值结果验证

通常弹头在明胶中的运动规律和明胶中的瞬时空腔形态被用来判定数值结果与实验结果的一致程度。图2为数值结果与实验高速摄影拍摄的空腔形态及弹头运动姿态对比。可以看到，在0～120 μs时间段弹头飞行较稳定，没有发生较明显的失稳翻滚，瞬时空腔形态类似一个细长的锥体;120～280 μs 时间段弹头发生了较明显的翻滚运动，大约280 μs 时弹头翻滚了大约90°.通过对比可以发现，数值结果与实验结果主要现象一致，数值结果较好地再现了弹头在明胶中的运动情况。弹头在明胶中的侵彻深度对比(见图3)表明，数值结果与实验结果的误差较小，这表明所建数值模型及采用的数值方法具有较高的精度。

表2 明胶状态方程参数Tab.2 The equation of state of ballistic gelatin

图2 数值结果与高速摄影结果对比Fig.2 Comparison of the penetration process between numerical and experimental results

图3 侵彻深度随时间变化Fig.3 Penetration depth vs.time

2 数值结果分析

2.1 弹头受到的明胶阻力分析

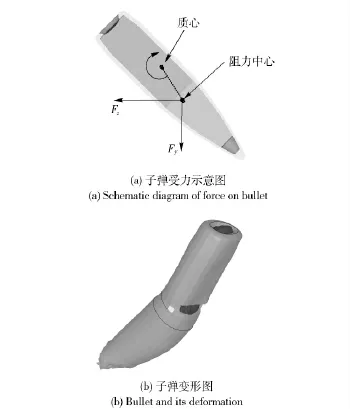
图4 子弹受力及变形示意图Fig.4 Schematic diagram of force applied on bullet and its deformation

由于明胶密度是空气的800 多倍，当步枪弹侵入明胶后会受到非常大的阻力作用，从而发生失稳翻滚甚至破碎。对弹头在明胶中的受力(图4(a))进行分析(忽略重力)，Fz为弹头受到的水平方向阻力，Fy为弹头受到的铅垂方向阻力，这两个力的合力产生一个使弹头绕其质心翻转的力矩。图5表明，在侵彻深度为0～130 mm 时，z 向阻力缓慢增长到大约3 000 N，而y 向阻力只有几百牛顿。在130～220 mm 段，随着弹头在明胶中失稳翻滚，其受力面积急剧增加，受到的明胶z 向阻力迅速增加至约15 000 N，同时y 向阻力的快速增加加速了弹头的翻滚。当侵彻深度达到约220 mm 时y 向阻力开始反方向作用于弹头，这表明弹头的翻滚速度开始减小，并开始产生回转。由于明胶阻力的作用和弹头本身的结构特点，弹头翻转了大约60°后开始沿辊沟处发生断裂，最终破碎成许多弹片(见图6)。数值分析发现，弹头辊沟处的应力集中较严重且铅芯易变形，因此在受到较大阻力作用后弹头易从该处断裂。图4(b)为弹头翻转了约90°时，数值方法得到的弹头在明胶中的变形情况。从图中可以看出，此时被甲中部靠近辊沟位置发生了明显断裂、弹头后半部分变扁且尾部有铅露出。

图5 明胶阻力随侵彻深度变化Fig.5 Penetration resistance vs.penetration depth

图6 实验中子弹侵入明胶740 μs 时的侵彻断面照片Fig.6 Experimental photo of gelatin at 740 μs

2.2 明胶中的等效应力分析

当明胶某处的等效应力超过临界值时，材料即发生屈服，产生不可逆的塑性变形，并有可能发生破坏。图7中4 个典型时刻的等效应力图表明，最大等效应力始终出现在瞬时空腔的外轮廓部位，随着空腔的不断膨胀，最大等效应力层所包含的面积也不断增大，即塑性区与弹性区不断增大。200 μs 时整个空腔呈近似圆柱状，到500 μs 时由于子弹的急剧翻滚，弹头将大量动能传递给周围的明胶，随后在该处迅速形成一个不断增大的拟球状的瞬时空腔，这部分明胶的应力层面积较大，对明胶造成的损伤也最严重。瞬时空腔现象是子弹侵彻明胶过程的主要物理现象之一，同时也是弹头的主要致伤方式。

图7 明胶中的等效应力分布Fig.7 Stress distribution contours at different times

2.3 攻角对杀伤效应的影响

在数值模型中设定子弹分别以相同速度不同攻角(0.7°、1°和2°)侵入明胶，研究攻角变化对子弹明胶相互作用过程的影响规律。图8表明，攻角越大，弹头翻转越早，翻转位置越靠近入口。攻角从0.7°增加到1°弹头从入射到翻转约90°所需时间提前了60 μs，翻转位置提前了42 mm.但是，攻角从1°增加到2°弹头从入射到翻转约90°所需的时间仅提前了20 μs，翻转位置仅提前了16 mm.这表明攻角较小时，攻角的微小变化对子弹在明胶内的翻转位置即最大空腔位置影响较大，随着攻角增大，攻角对弹头翻转位置的影响逐渐减小。

不同攻角下弹头在明胶中的速度衰减曲线(见图9)表明，弹头的速度衰减经历了两个明显的阶段即平缓衰减段和快速衰减段。在窄伤道段，弹头翻转角较小，受力面积较小，因此速度衰减较慢。随着子弹发生明显翻转，其受力面积也快速增加，因此弹头速度在短时间内急剧减小，将大量动能传递给周围明胶，最终在该位置形成最大瞬时空腔。

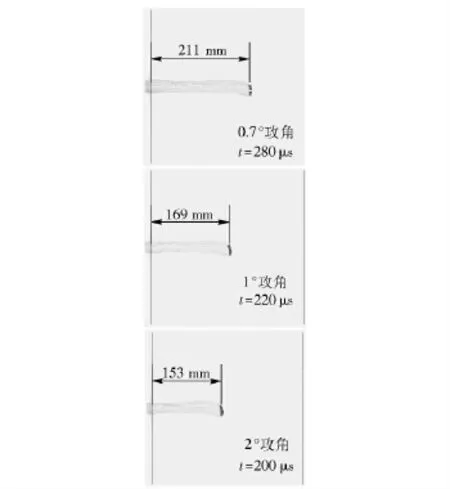
图8 不同入射攻角对弹头在明胶中翻滚位置影响的对比Fig.8 Comparison of the overturning moments of bullet at different angles of attack

从图中还可以看出，攻角的变化对窄伤道段的速度衰减影响较小，但对子弹翻转段的速度衰减有较大影响。攻角大的弹头比攻角小的弹头翻转位置靠前，速度先急剧减小;攻角小的稳定飞行距离更长，速度进入快速衰减段较晚。

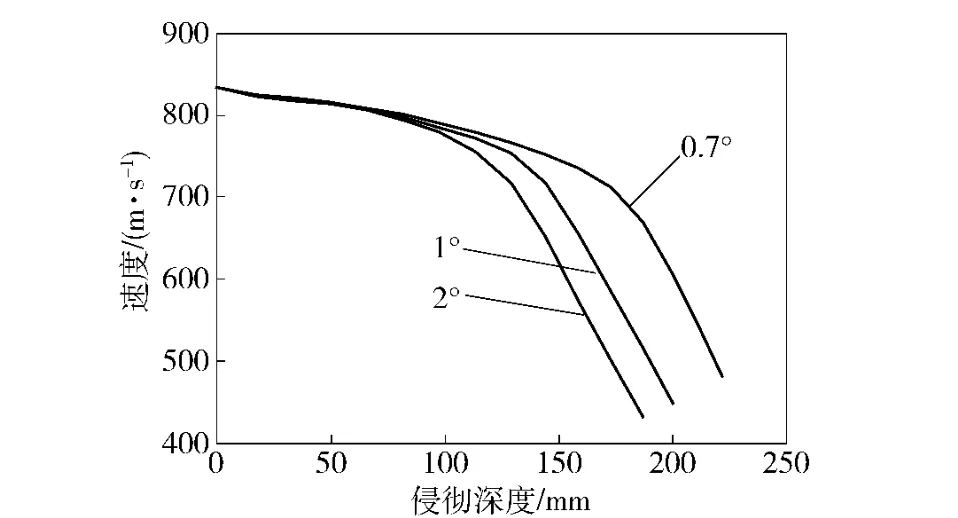
图9 不同入射攻角下的弹头速度衰减Fig.9 Velocity vs penetration depth at different angles of attack

3 结论

本文建立了步枪弹侵彻明胶的有限元模型，通过与实验数据对比验证了模型的有效性和准确性。基于数值结果深入分析了弹头与明胶的相互作用过程，并对初始攻角对弹头侵入明胶后运动的影响作了分析。基于以上分析得到如下结论:

1)弹头受到的明胶阻力及其自身结构特点使弹头在明胶中发生了翻滚，随着翻滚角度的增加，弹头受力面积增加，使明胶阻力急剧增加，弹头最终在明胶中发生了破碎。

2)明胶中的最大等效应力层始终分布在瞬时空腔的内壁，随着空腔的膨胀，明胶中的塑性区和弹性区不断增大。在弹头翻滚位置，由于弹头将大量动能传递给周围明胶，这一位置形成的瞬时空腔体积最大，明胶的应力层面积也较大，对明胶造成的损伤也最严重。

3)攻角较小时，攻角的微小变化对子弹在明胶内的翻转位置即最大空腔位置影响较大，随着攻角增大，攻角对弹头翻转位置的影响逐渐减小。

4)攻角的变化对窄伤道段的速度衰减影响较小，但对子弹翻转段的速度衰减有较大影响。攻角大的弹头比攻角小的弹头翻转位置靠前，速度先急剧减小，攻角小的稳定飞行距离更长，速度进入快速衰减段较晚。

References)

［1］ Dyckmans G，Nolompetelo N，Chabotier A.Numerical and experimental study of the impact of small caliber projectivles on ballistic soup［J］.EDP Sciences，2003，110(9):627 -632.

［2］ Salisbury C P，Cronin D S.Mechanical properties of ballistic gelatin at high deformation rates［J］.Experimental Mechanics，2009，49(6):829 -840.

［3］ Kwon J，Subhash G.Compressive strain rate sensitivity of ballistic gelatin［J］.Journal of Biomechanics，2010，43(3):420 -425.

［4］ Datoc D.Finite element analysis and modeling of a.38 lead round nose ballistic gelatin test［D］.California:California Polytechnic State University，2010.

［5］ Koene L，Papy A.Experimental and numerical study of the impact of spherical projectiles on ballistic gelatin at velocities up to 160 m/s［C］∥25th International Symposium on Ballistics.Beijing:IBC，2010:1573 -1579.

［6］ Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperature［C］∥Proceedings of the 7th International Symposium on Ballistics.Hague，Netherlands:IBC，1983:541 -547.

［7］ Jenq S，Hsiao F，Lin I，et al.Simulation of a rigid plate hit by a cylindrical hemi-spherical tip-ended soft impactor［J］.Computational Mater Science，2007，39(3):518 -526.

［8］ Ensan M N，Zimcik D G，Lahoubi M，et al.07-CSME-66-Soft body impact simulation on composite structures［J］.Transactions of the Canadian Society for Mechanical Engineering，2008，32(2):283 -296.