复合装药结构隔板实验与数值模拟

向梅，黄毅民，饶国宁，彭金华

(1.南京理工大学 化工学院，江苏 南京210094;2.中国工程物理研究院 化工材料研究所，四川 绵阳621900)

0 引言

在战斗部装药中，常常将钝感炸药和高能炸药组成复合结构使用，这样的结构既解决了钝感弹药的能量输出较小的问题，又在一定程度上保证了整体装药结构具有一定的安全性。多年来国内外学者都对其作了大量的研究。Aminov 等［1］对以TATB为基的炸药冲击波感度实验进行了数值模拟研究，建立了其以热点假说为前提的动力分解模型;Kobylkin 等［2］设计了一种测试冲击波感度的实验方法，并得到了不同装药的冲击波感度的定量数值;陈熙蓉等［3］准确地测量了冲击波在不同材料隔板中的行进距离随时间的变化关系，计算得到了隔板中不同厚度处的冲击波速度和冲击波压力;王慧君等［4］将炸药的水下爆炸能量测试方法与冲击波感度测试方法相结合，得到6 种炸药冲击波感度的相对排序;刘玉存等［5-6］采用SSGT 小隔板试验揭示了主体炸药HMX 粒度和粒度级配对塑料粘结炸药冲击波感度和爆炸输出能量的影响以及炸药粒度对热点点火过程的影响;曾代朋等［7］将数值计算的方法引入隔板实验中，并验证了实验值和计算值的一致性。目前对复合装药的冲击波感度还很少见到报导，本文对复合装药结构的冲击波感度进行了实验研究，结合数值计算，对不同隔板厚度的冲击起爆及反应阈值以及不同的隔板材料的冲击波感度进行了分析。

1 实验方法和数值模拟

1.1 隔板实验

隔板实验是在标准主发药和被发药之间加惰性隔板，主发药柱产生的冲击波经过惰性隔板材料衰减后作用于被发药端面，通过改变隔板厚度，或变换冲击阻抗不同的隔板材料，调节输入被发药中的冲击波强度并阻挡主发药的爆炸产物对被发药的冲击加热作用，测定发生爆轰的隔板厚度，其一定爆轰率的隔板厚度简称隔板值，以此表征试样的冲击波感度，隔板值越大，表明炸药对冲击波越敏感。

隔板实验程序参考的标准为GJB772A—1997炸药试验方法(方法605.1 冲击波感度—卡片式隔板法)。实验步长为1.14 mm，有效实验次数不小于20 次，实验后如见证板上有明显的孔，判为爆轰，否则判为未爆轰。试样50%发生爆轰的隔板值G50依据上述标准中的方法进行计算得到。

图1 实验装置示意图Fig.1 Schematic diagram of experiment assembly

隔板实验装置如图1所示，隔板材料采用LY12，主发药柱用φ20 mm×40 mm 的高能炸药JO-9159 炸药，密度为1.860 ±0.002 g/cm3.待测复合药柱的尺寸为φ20 mm×40 mm，上层为钝感炸药JB-9014(密度为1.888 ±0.002 g/cm3)，下层为高能炸药JO-9159，其具体结构和尺寸见图2.

图2 待测试样结构示意图Fig.2 Schematic diagram of tested explosive

对4 种不同结构的复合装药进行隔板实验结果列于表1中，可以看到随着被发药柱端头的钝感炸药厚度的增加，复合装药的冲击波感度G50值与x =h1/(h1+h2)呈一阶指数衰减关系:

式中e 为某常量。

表1 隔板实验测试结果Tab.1 Gap tests results

图3 复合药柱G50值与h1/(h1 +h2)的关系Fig.3 The relationship between G50 and h1/(h1 +h2)of composite charge cylinder

从图3可以看到复合装药结构的隔板值介于高能炸药和钝感炸药之间，受钝感炸药的影响明显，采用该结构在冲击波载荷下的安全性明显高于单一高能炸药装药。

1.2 数值模拟

利用显式有限元程序AUTODYN 对上述实验进行模拟。由于复合药柱为轴对称几何结构，因此在计算时建立二维模型，如图4所示。网格大小为0.5 mm×0.5 mm.炸药和空气选择Euler 求解器，隔板选择Lagrange 求解器，在被发药柱轴向设置10 个测试点。

图4 数值模拟模型Fig.4 Numerical simulation model

炸药模型采用点火增长模型［8-10］，假设点火起始于系统热点，并从这些热点开始延伸增长。

式中:F 为化学反应度;p 为压力(GPa);v，v0为炸药比容;I、G1、G2、a、b、c、d、e、g、x、y、z 为相关常数，具体值见下表。(2)式右边第1 项为热点的形成及点火，第2 项为热点的反应成长，第3 项为反应的快速完成。

表2 炸药点火增长模型参数Tab.2 Ignition and growth model parameters of explosives

空气材料选择理想气体状态方程，密度ρ =0.001 225 g/cm3，多方指数γ=1.4，定容比热容Cv=0.717 6 J/(g·K);隔板材料LY12 满足冲击绝热关系us=c0+λup.其中us为冲击波速度;up为波后粒子速度，c0=3 320 m/s，λ =1.424，密度ρ =2.8 g/cm3，Gruneisen 系数为2.

在上下结构复合装药条件下，由于采用的点起爆方式，在柱形装药结构中产生曲面爆轰波，衰减后的冲击波曲率半径变大，继续在钝感炸药中传播，冲击波在两种不同炸药的交界面处发生反射和折射后，继续在高能炸药中传播。其间的传播过程较为复杂，取决于两种药的爆轰性能、隔板材料、隔板厚度、以及试样的结构比例。

在数值模拟情况下，通过观察模型中不同位置的压力峰值的变化趋势来判定复合装药是否发生了爆轰。图5为复合装药发生爆轰的情况，沿着爆轰波传播的方向，测试点压力峰值逐渐上升。图6为“未爆轰”的情况，测试点的压力峰值随时间增加呈下降状态。

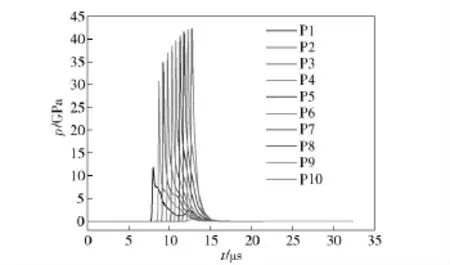
图5 检测点压力-时间曲线1Fig.5 p-t curve 1 of the test points

图6 检测点压力-时间曲线2Fig.6 p-t curve 2 of the test points

依据上述判定方法，分别对上述4 种复合结构进行数值模拟，结果如表3所示，数值模拟误差小于8%，表明构建模型合理，结果可信。

表3 实验模拟比对结果Tab.3 Comparison between the experimental and simulated results

2 计算结果与分析

2.1 冲击起爆反应阈值

为了得到复合药柱的冲击起爆阈值，利用前文所构建的模型模拟了隔板材料为LY12，h1为10 mm，h2为10 mm 时，不同隔板厚度下的入射压力峰值及∫p2dt 值，计算结果如表4所示，对应的入射压力波形如图7所示。由表4可以看出隔板厚度由8 mm变化到12 mm，压力峰值由16.9 GPa 下降到11.4 GPa，而幅度较大，因此用值来评估炸药的冲击起爆及反应阈值更加合理［7］。

表4 不同厚度隔板的入射压力峰值及∫p2dt 值Tab.4 The incident peak pressure and∫p2dt in different gap thickness

2.2 不同隔板材料

对于复合装药结构的∫p2dt 的计算只需要考虑隔板材料的冲击阻抗不同对入射波的衰减影响。为了使各种材料具有可比性，选择被测药h1为0 mm，h2为20 mm，即被测药为JO-9159 炸药的结构，分别以LY12、有机玻璃、45#钢为隔板材料进行模拟计算，同时将钝感炸药JB-9014 作为隔板材料也进行比较计算。空气材料和LY12 的状态方程及参数同1.2 节，有机玻璃、45#钢、未反应JB-9014 亦满足冲击绝热关系，其参数见表5，JB-9014 炸药仍采用点火增长模型，其参数见表2.

图7 不同厚度隔板的入射压力波Fig.7 The incident pressure curves of different gap thickness

表5 不同隔板材料物性参数Tab.5 The parameters of different gap materials

计算结果见表6所示，入射压力波形如图8所示。

表6 不同隔板材料的计算结果Tab.6 The calculated results of different gap material

由计算结果可知，被测炸药的铝隔板值最大，其次是有机玻璃隔板值，钢隔板值最小。JB-9014 作为未反应炸药和反应炸药得到的隔板值一致。未反应JB-9014 在充当隔板材料时，将其视为惰性材料;而JB-9014 充当隔板材料时，将其视为可发生反应的正常炸药。实际上表现了主发药冲击波在钝感炸药中非理想爆轰作用后能否使被发的JO-9159发生爆轰，与钝感材料对冲击波的衰减作用不同，这里的隔板厚度值不能作为评价炸药冲击波感度的依据。在隔板厚度相同时，钢中的冲击波压力最高，但衰减最快，在有机玻璃中压力最低，衰减慢。

图8 不同隔板材料入射压力波Fig.8 The incident pressure curves of different gap material

铝、有机玻璃、钢隔板和未反应JB-9014 炸药的爆轰反应阈值在9～12 GPa2·s 左右，而以钝感炸药JB-9014 为隔板材料时，其隔板值介于铝、有机玻璃隔板值和钢隔板值之间，由于其本身存在化学反应，因此得到的∫p2dt 值不能作为爆轰反应阈值。

3 结论

1)从4 种不同结构的复合装药的隔板实验结果看到随着被发药柱端头的钝感炸药厚度增加，复合装药的冲波感度G50值与x =h1/(h1+h2)成一阶指数衰减关系，装药时采用复合装药结构能够提升整体装药的安全性;

2)利用显式有限元软件AUTODYN 对隔板实验进行数值模拟，得到的结果与实验结果吻合;

3)用∫p2dt 值评估隔板实验的爆轰反应阈值较为合理，通过数值计算发现钝感材料铝和有机玻璃对冲击波的衰减作用近似，得到接近的隔板值，钢隔板由于其内冲击波衰减较快，得到的隔板值较小。而以JB-9014 作为未反应炸药和反应炸药得到的隔板值一致，介于铝、有机玻璃隔板值和钢隔板值之间，但不能将反应JB-9014 炸药的∫p2dt 值作为炸药的起爆反应阈值的依据。

References)

［1］ Aminov Y A，Vershinin A V，Es'kov N S，et al.Shock-wave sensitivity of a TATB-based plasticized explosive［J］.Combustion，Explosion and Shock Waves，1995，31(1):100 -105.

［2］ Kobylkin I F，Nosenko N I，Solov'ev V S.Experimental investigation of the change of the shockwave sensitivity of explosives due to weak precursor waves［J］.Combustion，Explosion，and Shock Waves，1992，28(6):636 -639.

［3］ 陈熙蓉，王可，刘德润，等.冲击波在不同材料隔板中的衰减特征［J］.兵工学报，1991，12(2):75 -80.CHEN Xi-rong，WANG Ke，LIU De-run，et al.Characteristics of attenuation of shock waves in barries of different materials［J］.Acta Armamentarii，1991，12(2):75 -80.(in Chinese)

［4］ 王慧君，陈网桦，何中其，等.用水下卡片间隙实验法测定炸药冲击波感度［J］.爆炸与冲击，2009，29(5):481 -485.WANG Hui-jun，CHEN Wang-hua，HE Zhong-qi，et al.Shock sensitivity measurement of explosives by an underwater card gap test method［J］.Explosion and Shock Waves，2009，29(5):481 -485.(in Chinese)

［5］ 刘玉存，王作山，柴涛，等.HMX 粒度及其级配对塑料粘结炸药冲击波感度和爆炸输出能量的影响［J］.兵工学报，2000，21(4):357 -360.LIU Yu-cun，WANG Zuo-shan，CHAI Tao，et al.Influence of HMX particle size and gradation on the shock sensitivity and output of a PBX explosive［J］.Acta Armamentarii，2000，21(4):357 -360.(in Chinese)

［6］ 刘玉存，王作山，吕春玲，等.黑索今粒度及粒度级配对高分子粘结炸药冲击波感度的影响［J］.兵工学报，2005，26(1):126 -128.LIU Yu-cun，WANG Zuo-shan，LYU Chun-lin，et al.Influence of particle size and gradation of RDX on the shock sensitivity of a polymer bonded explosive［J］.Acta Armamentarii，2005，26(1):126 -128.(in Chinese)

［7］ 曾代朋，谭多望，李尚斌，等.含铝炸药冲击波感度的实验和数值计算研究［J］.含能材料，2010，18(2):148 -151.ZENG Dai-peng，TAN Duo-wang，LI Shang-bin，et al.Experimental and numerical calculation study on shock sensitivity of aluminum explosive［J］.Chinese Journal of Energetic Materials，2010，18(2):148 -151.(in Chinese)

［8］ 梁增友，黄风雷，张震宇.PBX-9404 的化学反应速率方程及起爆特性［J］.爆炸与冲击，2008，28(1):38 -43.LIANG Zeng-you，HUANG Feng-lei，ZHANG Zhen-yu.Study on new reaction rate function model of PBX-9404 for damaged explosive initiation behavior［J］.Explosion and Shock Waves，2008，28(1):38 -43.(in Chinese)

［9］ 李金河，文尚刚.用三项式点火增长反应速率模型计算JB-9014 的反应区［J］.高能量密度物理，2007，(2):47 -54.LI Jin-he，WEN Shang-gang.Study on reaction zone calculation of JB-9014 by usingthree term equation ignition and growth model［J］.High Energy Density Physics，2007，(2):47 -54.(in Chinese)

［10］ Tarver C M，Hallquist J O，Erickson L M.Modeling short pulse duration shock initiation of solid explosives［C］∥Proceedings of the 8th International Symposium.Albuquerque，New Mexico，USA:UCRL，1985:951 -961.

［11］ 韩勇，鲁斌，蒋志海，等.JO-9159/ECX 复合装药的冲击波感度研究［J］.含能材料，2008，16(2):164 -166.HAN Yong，LU Bin，JIANG Zhi-hai，et al.Shock sensitivity of JO-9159/ECX composite charge［J］.Chinese Journal of Energetic Materials，2008，16(2):164 -166.(in Chinese)