一种基于BOC 信号的多径抑制技术

邵兴权，宗竹林

电子科技大学 电子科学技术研究院，成都611731

1 引言

BOC 调制是未来卫星导航系统中非常重要的一种调制方式，其独有的功率谱裂谱特性可以实现频段共用的同时实现频谱分离，减小信号之间的相互干扰，可以很好地解决导航频段拥挤导致的频谱混叠和干扰等问题。与传统的BPSK 调制信号相比，相同速率的BOC 调制信号具有更加陡峭的自相关峰，因此具有更高的跟踪精度。BOC 信号的这些优点，使得BOC 体制受到十分广泛的关注，也必然会应用于我国的北斗卫星定位系统中。

本文在ELS（Early Late Slope）[1]技术基础上，针对多径信号对直射信号自相关峰造成的不对称影响，结合BOC调制信号多尖峰的特性，提出了一种基于最大似然估计的加权ELS 多径减弱方法。本文的主要思想是，根据BOC 信号自相关函数对直射信号做一个最大似然估计，得到直射信号自相关函数后，根据相关峰两边的斜率，计算一个系数反映该相关峰的不对称影响，并将这个系数作为反馈因子以减小误差。由于BOC 信号自相关函数具有多个尖峰，对每一个尖峰进行斜率检测都将得到一个多径干扰系数，将这几个系数进行加权组合得到的新系数作为反馈因子，将进一步减小误差。

2 多径干扰分析

接收信号经过杂波剥离后的多径模型[2]可以表示为式：

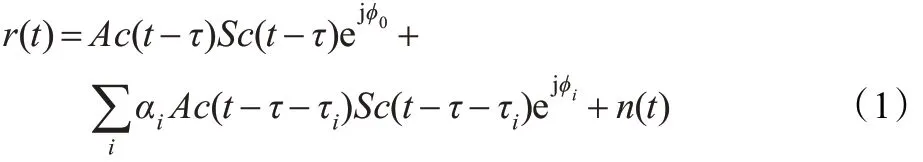
其中，c(t)表示扩频符号，Sc(t)表示副载波，A 表示信号幅度，τ 表示传播延迟。等式前面部分表示直射信号，后面表示有多条多径反射信号。不妨以一条反射信号为例，可以表示为：

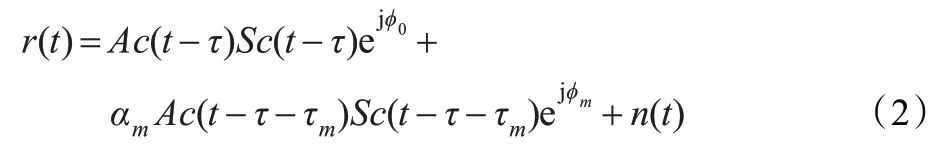
其中，αm、τm和φm分别表示反射信号相对幅度、延迟和相位。n(t)表示噪声。

接收信号经过点乘（Dot Product）接收机后，输出可以表示为：

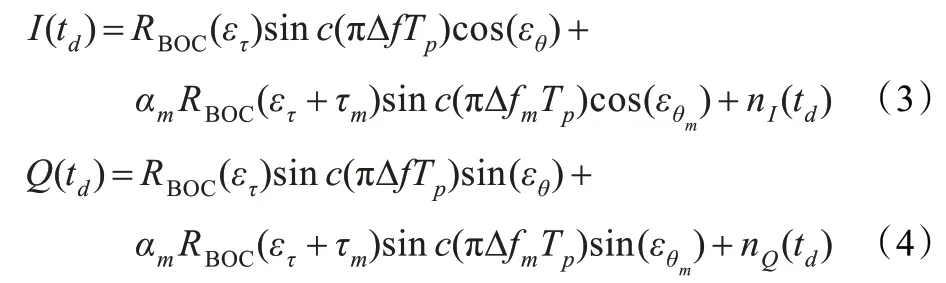
其中，εθ是直射信号上的码相位跟踪误差，εθm是反射信号上的码相位跟踪误差，Δf 是直射信号上的多普勒误差，Δfm是反射信号上的多普勒误差。根据接收机输出信号可以发现，多径干扰可以描述为，反射信号的自相关函数对原来的直射信号相关函数的形状扭曲和时移。在接收机的DLL 跟踪信号时，多径干扰会引入一个偏移，产生多径误差。当直射信号和反射信号同相或反相时，多径误差达到最大，即εθ-εθm=0 或者εθ-εθm=π。

图1 给出了BOC（10，5）的归一化自相关函数（direct path）、一条反射信号的自相关函数（reflected path）和叠加过后的自相关函数。设定参数αm=0.5，εθ-εθm=0，τm=0.8个码片。

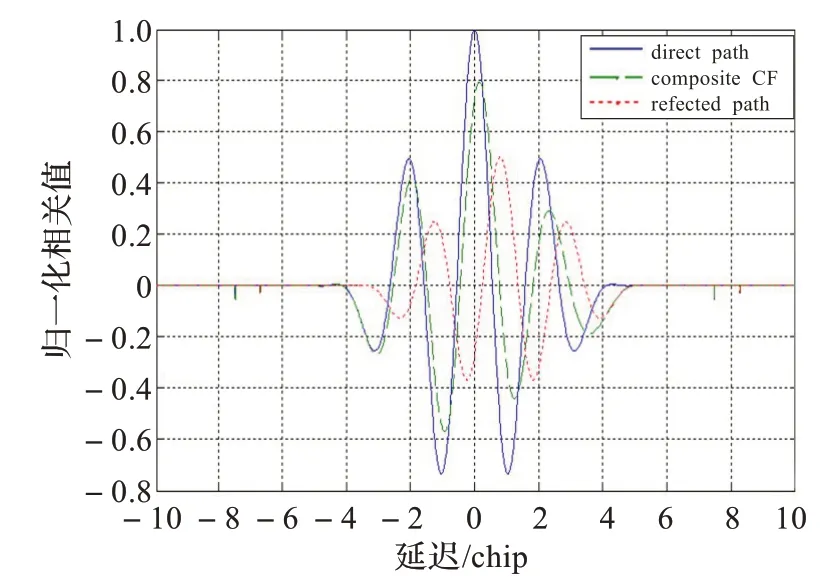
图1 多径干扰直射信号、反射信号与叠加信号相关函数

图2（a）给出了无多径干扰[3]（S-curve without multipath）和有多径干扰（S-curve with multipath）情况下的S-曲线。图2（b）更加清晰地显示了多径干扰使得跟踪锁定点偏离了（0，0）位置，这就导致了跟踪误差。

3 最大似然多径估计模型

多径估计技术[4]可以看做是从测量变量到估计变量的一种线性变换。设aj为第j 路多径信号幅度，τj为第j 路多径信号延迟。不考虑载波影响，则输入信号为：

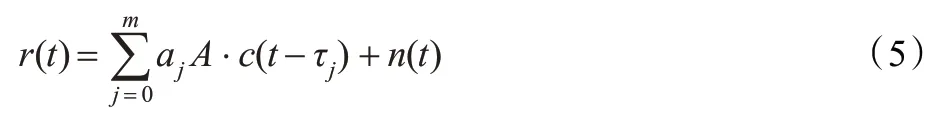
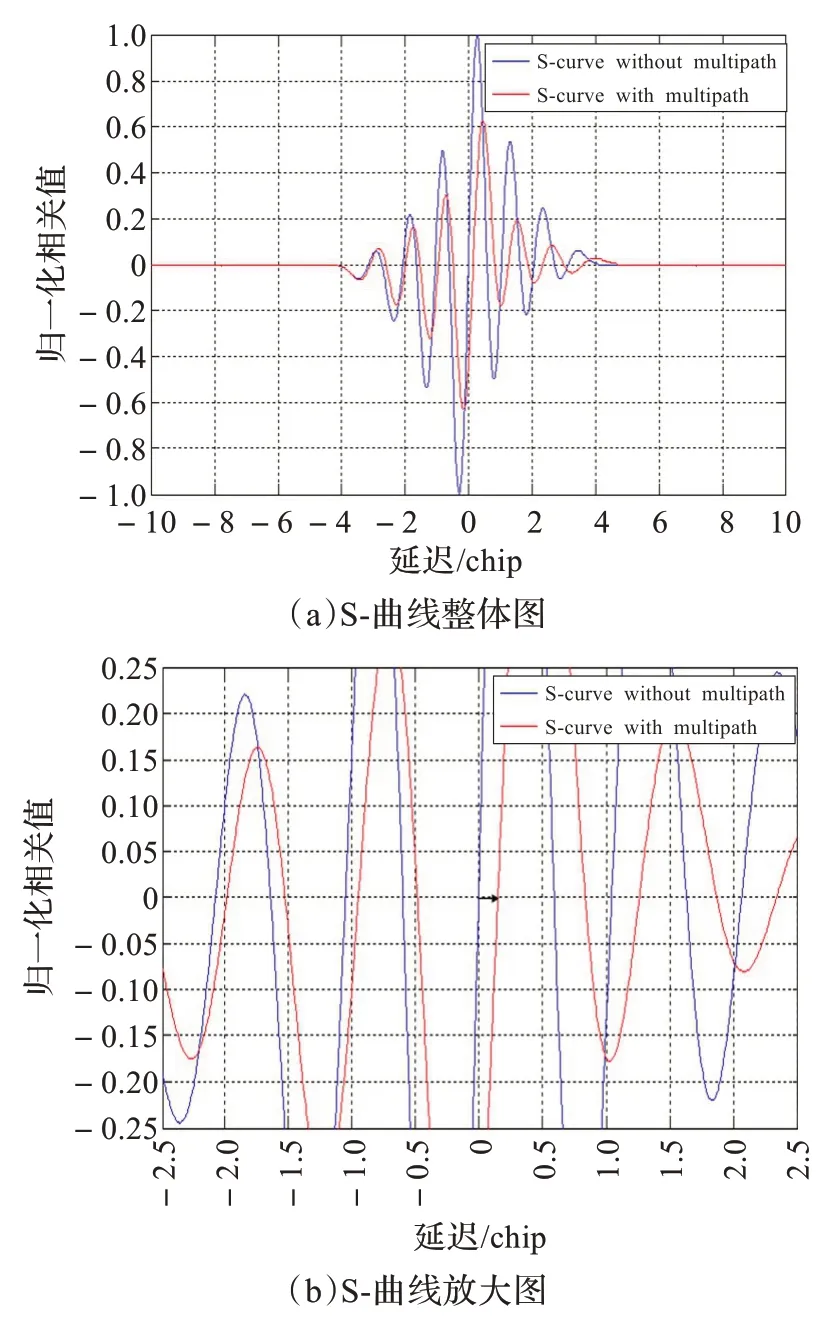
图2 有多径干扰和无多径干扰下的S-曲线

相干积分累加过程为

其中，βi表示i 路多径信号的延迟的估计值；n 为本地产生的码延迟数；m 为实际多径数；y 为观测列向量；w 为通过相关器[5]后的噪声向量。式（6）用矩阵表示为：

先不考虑噪声的影响，采用最小二乘估计，含多径延迟的幅度估计值为：

具体方法是通过对τj的估计（多径延迟估计βi在[0，1.5 Tc]范围才会对码跟踪产生影响），使得|y-Ha|最小。

多径参数的最大似然估计相对于最小二乘估计多了对噪声w 的处理。令噪声w=[w0,w1,…,wn] 的方差为Cw，则：

其中

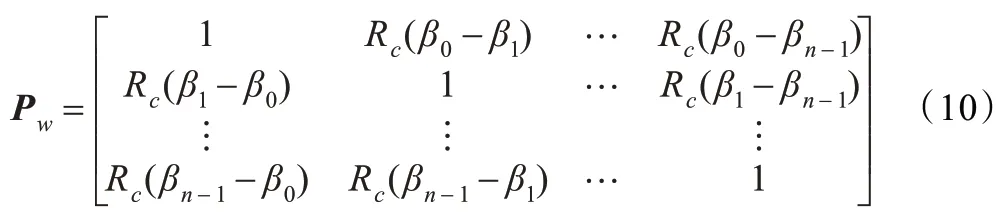
因此w～N(0,Cw)，y～N(Ha,Cw)。从而得到最大似然估计为：

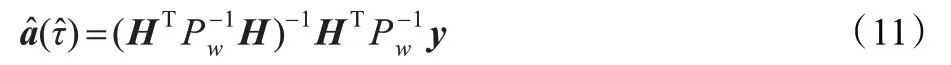
其中

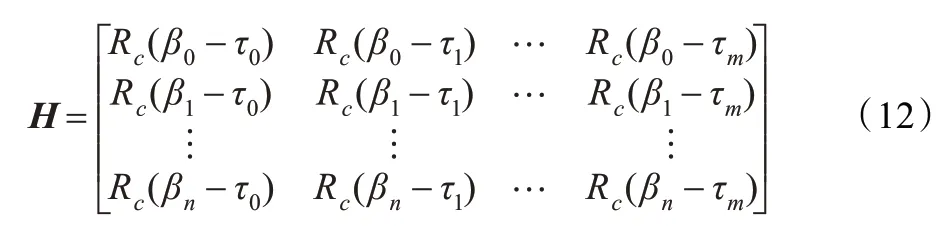
以BOC（10，5）为例，设直视信号幅度为1，延迟为0，加入5 路多径信号，则直视信号和多径信号幅值a =（1，0.2，0.6，1.6，0.9，0.5），码相位延迟τ =（0，0.1，0.3，0.5，0.9，1.3）。码相位延迟搜索范围β ∈[0,1.5]，搜索步长为0.1。利用式（8）可得到最小二乘估计[6]如图3 所示。由仿真结果可以看出，幅度估计值与实际多径信号幅度完全吻合。

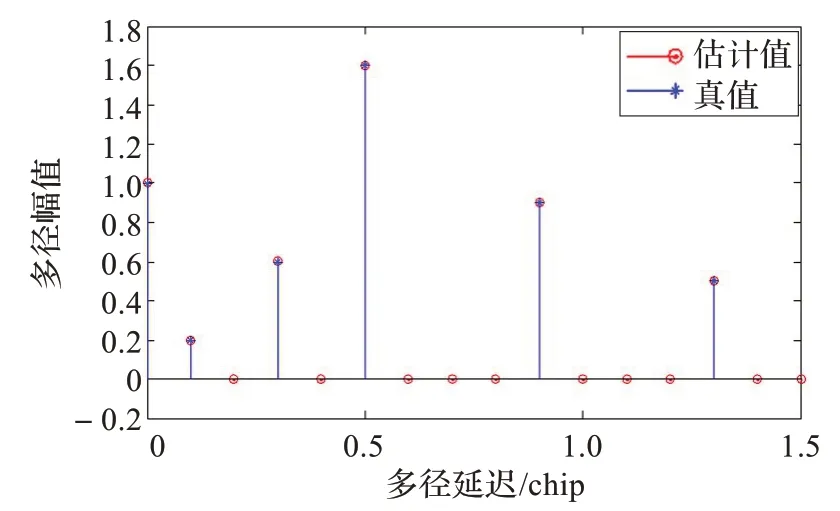
图3 无噪声时的最小二乘多径估计

由式

可得噪声方差。其中c/n0为载噪比，T 为相干积分累加时间。设定载噪比为40 dB-Hz，相干积分累加时间为20 ms，利用式（11）可得最大似然估计如图4。从图中可以看出，由于噪声的存在，使得估计出现了误差，但总体上仍然可以体现多径估计值。

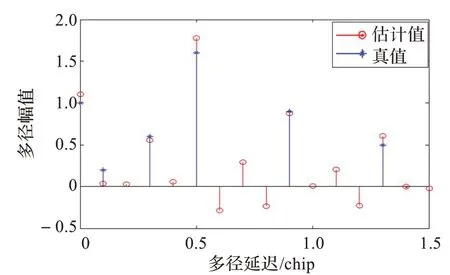
图4 有噪声时的最大似然估计

当多径信号落在两个观测点之间，可以认为该信号分解到了相邻的两个估计点上[7]。分解规则满足式

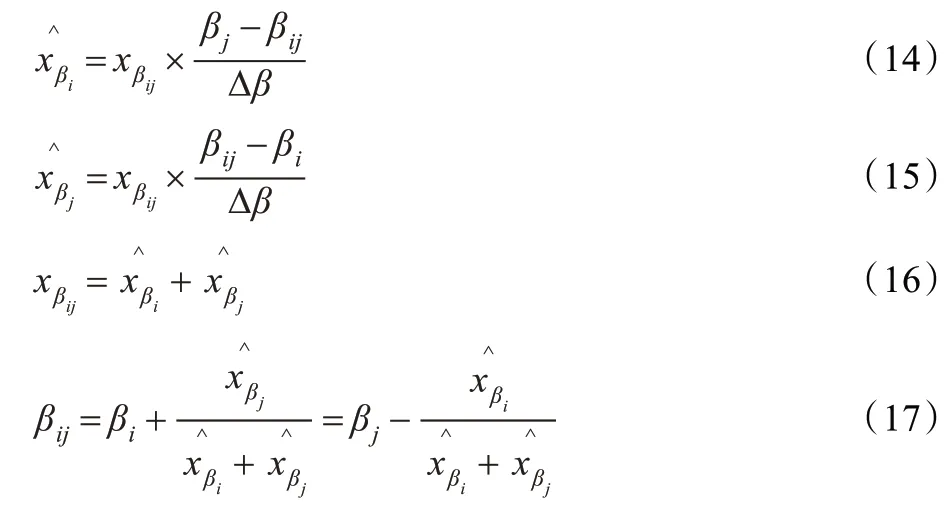
其中，βi和βj为相邻两个观测点时刻，和为两个相邻观测点得到的观测幅度，Δβ 为相邻时刻时间差，xβij为实际多径信号幅度，βij为实际多径信号延迟。由该组公式可知，观测直射信号是实际直射信号与某条或多条延迟相近多径信号的叠加，因此观测直射信息不可作为直射信号的估计。较合理的处理方式，应该是用原始信号减去多径信号观测值。输入信号、直射信号与估计直射信号如图5。

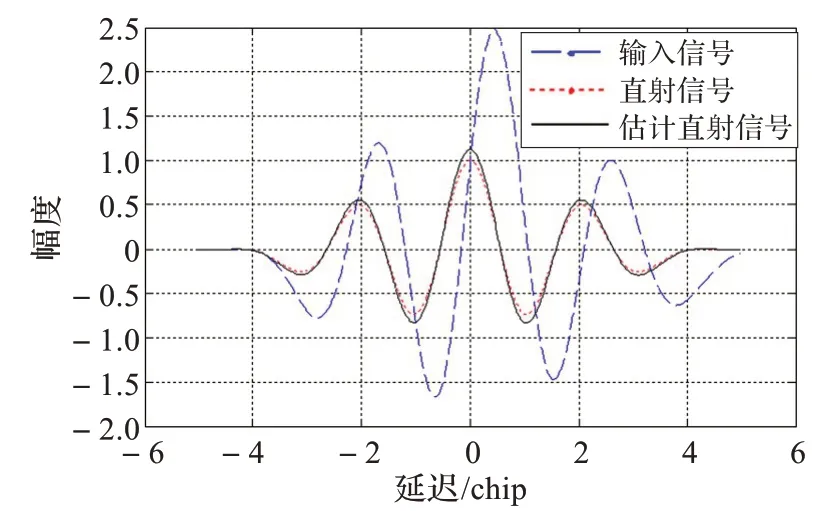
图5 输入信号、直射信号与估计直射信号

这样估计出的直射信号包含了噪声和较少的一部分多径分量，可以采用加权ELS 方法进一步减小跟踪误差。ELS 技术的主要思想是计算自相关函数主峰两边的斜率，原理如图6 所示。从图中可以看出，在接收机带宽一定的条件下，自相关函数尖端会变得圆滑一些。在多径干扰的情况下，其自相关峰由于多径信号的叠加而变得扭曲。假设左边直线斜率为a1，右边直线斜率为a2，则反馈因子ζm可以表示为：

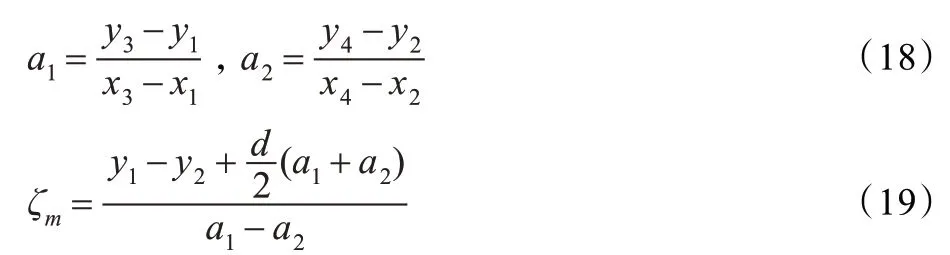
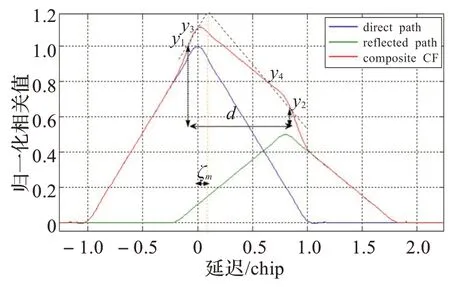
图6 对BPSK 的ELS 技 术

与BPSK 信号相比，BOC 信号的自相关函数具有多个峰，可以在多个峰上运用ELS 技术[8]。加权ELS 技术的主要思想就是计算多个峰两边的斜率，并根据斜率计算这些反馈系数，每个反馈系数都可以用来纠正误差，因此最终的反馈因子就是这些系数的加权组合。加权ELS 技术原理如图7 所示。反馈因子可以表达为：

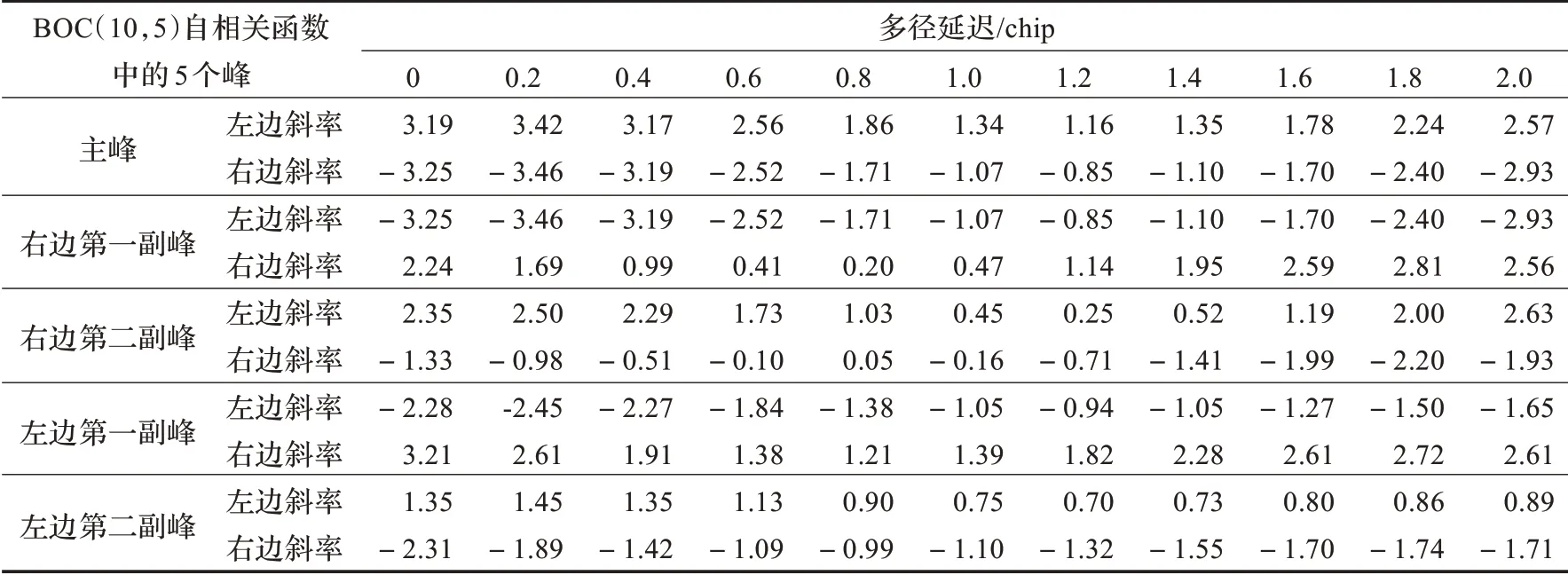
表1 斜率数值列表

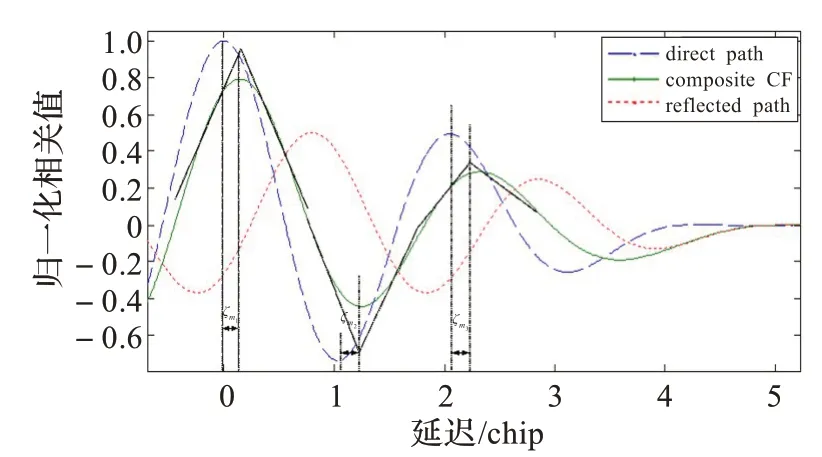
图7 对BOC 信号的加权ELS 技术

其中，αk为权重，Tsc表示副载波周期，这里表示相邻两个峰之间相邻半个副载波周期。N表示经过ELS 技术处理过的峰数量，它可以等于或者小于BOC 自相关函数峰总数。直接对估计直射信号进行加权ELS 处理，有助于进一步减小跟踪误差。对BOC（10，5）自相关函数其中的5 个峰进行斜率检测的数值如表1。

根据公式（18）和公式（19），对单个峰值的ELS 技术计算相关峰两边的斜率只需要选用4 个点，整个计算过程只需要8 次加减法运算和4 次乘除法运算。加权ELS 是对BOC 信号自相关函数的N个峰进行运用ELS 技术，总共需要10N-1 次加减法运算和6N次乘除法运算，因此总体上说，加权ELS 技术的运算复杂度较低。

多径误差包络分析[9]是一种典型的比较不同估计方法多径性能的方法。该方法首先在信号中叠加一个多径分量。多径分量为直射信号的反射信号，故幅度必然小于直射信号；同时，如果多径分量幅度太小，则不会产生明显的多径误差。一般选择相对幅度为0.25 或0.50 的多径信号，能造成明显的多径干扰，具有一定的代表性。然后利用估计方法对信号直达路径进行相位估计，得到一个含有误差的估计包络。将不同的方法得到的包络进行对比，可以清楚的显示不同方法的差异。

图8 和图9 分别显示了BOC（10，5）和BOC（3，2）信号的多径误差包络图。其中加入多径信号相对幅度为0.5，包络的两条曲线分别是εθ-εθm=0 和εθ-εθm=π时的多径误差曲线，即最大误差曲线。误差包络最大的是运用点乘鉴别器的窄相关技术（narrow correlator），其次是只检测主峰两边斜率的ELS 技术，误差最小的是检测多个峰两边斜率的加权ELS 技术。由此可见，在抗多径干扰方面，ELS 技术比起窄相关技术有明显的优势，而加权ELS 技术在此基础上有更进一步的改进。

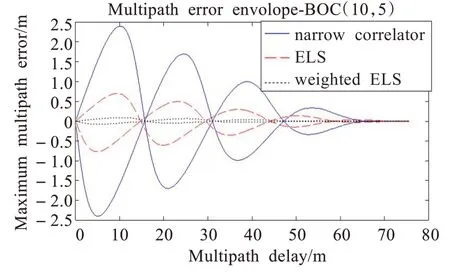
图8 多径误差包络-BOC（10，5）

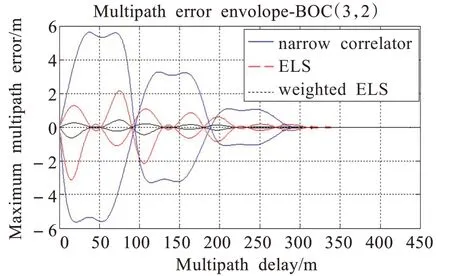
图9 多径误差包络-BOC（3，2）

4 结论

本文结合BOC 信号的自相关函数特性，通过分析多径干扰对BOC 自相关函数的作用以及对S-曲线的造成的偏移效果，提出了一种基于最大似然估计的加权ELS 技术，以减弱多径误差。仿真结果表明，载噪比为40 dB-Hz，相干积分累加时间为20 ms时，最大似然估计可以得到较精确的直射信号估计值。同时，相比于传统方法对BOC（10，5）和BOC（3，2）的加权ELS 技术的处理，本文方法能够以较小的计算复杂度代价获得更小的误差包络，从而有效地减小多径误差，提高跟踪精度。

[1] Jones J，Fenton P，Smith B.Theory and performance of the pulse aperture correlator[EB/OL].（2004-06-09）.http：//www.novatel.ca.

[2] Townsend B R，van Nee D J R，Fenton P C，et al.Performance evaluation of the multipath estimating delay lock loop[C]//Proceedings of ION NTM 1995，California，18-20 January，1995.

[3] 赵汪洋，杨功流，庄良杰.多导航传感器的多模卡尔曼滤波研究[D].天津：天津大学，2006.

[4] 朱笛，申功勋.基于小波分析的BOC 信号抗多径码相位估计[J].北京航空航天大学学报，2009，35（7）：828-832.

[5] Townend B R，Fenton P.A practical approach to the reduction of pseudorange multipath errors in a L1 GPS Receive[C]//Proceedings of ION GPS-94，Salt Lake City，September 1994.

[6] 邱致和.GPS M 码信号的BOC 调制[J].导航，2005，41（1）.

[7] Betz J W.Binary offset carrier modulation for radio navigation[C]//Proceedings of ION NTM 1995，California，January 1995：50-63.

[8] 杨力.基于BOC 调制的导航信号同步接收关键技术研究[D].南京：南京理工大学，2009-12.

[9] 何在民.BOC 信号的相关器设计及跟踪性能分析[D].北京：中国科学院研究生院，2008-05.