目标高程对SAR图像中目标位置偏差的影响

蒋 锐 朱岱寅 朱兆达

（1.南京邮电大学通信与信息工程学院，南京，210023；2.南京航空航天大学电子信息工程学院，南京，210016）

引 言

合成孔径雷达（Synthetic aperture radar，SAR）是一种全天候、全天时的现代高分辨率微波遥感成像雷达。它利用合成孔径原理、脉冲压缩技术，获得距离向和方位向高分辨的遥感图像，能够对地物目标进行大面积的成像。SAR至今已经取得了飞速的发展，被广泛地应用于国民经济和国防建设的各个领域，发挥了极其重大的作用［1］。

利用SAR干涉技术测量目标的高度信息，实现目标场景的三维成像是SAR遥感技术的重要应用之一。干涉合成孔径雷达（Interferometric synthetic aperture radar，InSAR）通过跨航迹观测，获取地面同一区域的复图像对，经过图像配准［2－3］、干涉处理、去平地效应［4］、降噪滤波［5－8］以及相位解缠绕［9－14］，可以得到复图像对间的绝对相位差。最后利用该相位差，计算所观测区域中各目标高度，从而实现全天候、大面积、高精度的三维地形测量。

然而在实际应用中，目标自身高度会引起目标在方位向和距离向上产生位移，从而导致数字地形高度图（Digital elevation model，DEM）中目标位置与实际观测场景中目标位置存在差异［1，15］。本文详细分析了图像中目标位移的原因，并具体推导了目标在方位向和距离向上的位移量与成像几何，目标高度之间的数学关系，提供了正确定位目标真实位置的方法。通过仿真实验，进一步验证了本文理论分析的正确性。

1 正侧视情况下的目标位置分析

假设载机沿X方向匀速直线运动，在正侧视情况下，载机视线所构成的斜平面与X方向平行，此时，目标投影至成像平面时，沿X方向不存在偏移。因此，在正侧视情况下，仅需要考虑目标自身高度对于目标成像位置在距离向上的影响。

1.1 理论分析

假设雷达位于S处，高度为H，与场景中心点O距离为R，其入射角为η。场景内任意目标P，当其高度为0时，该目标在斜平面的投影位置为P′；当其高度为ht时，如图1所示，该目标在斜平面的投影位置为P′1，对应地平面的投影位置为P1。

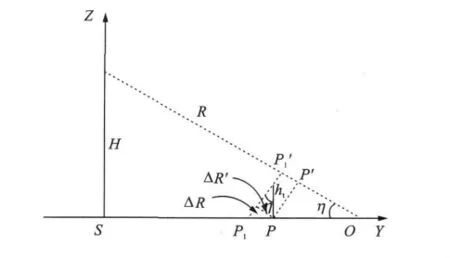
图1 正侧视情况下雷达成像几何

图1中可以明显看出当目标自身高度不为0时，其斜平面与地平面的投影位置都相应地产生变化。根据图1中的成像几何，可以简单推算出该目标在斜平面的投影位移ΔR′和地平面的投影位移ΔR分别为

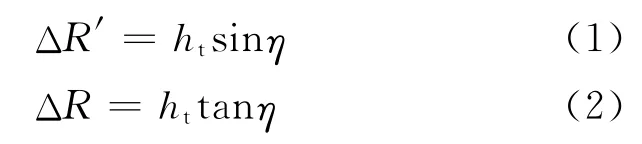
由式（1，2）可得

显然，ΔR′即地平面的位移量ΔR在斜平面的投影。由于载机高度H和雷达作用距离R已知，在正侧视条件下，有

将式（4）代入式（1，2）中，得到

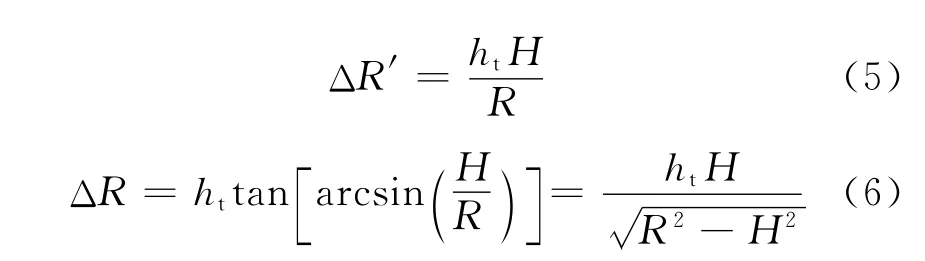
利用InSAR处理估计目标的高度信息ht，通过式（5－6），根据成像算法中距离向分辨单元长度，计算得到目标在图像中的位移量，可以将目标准确定位回其真实位置所对应的像素单元中。

1.2 仿真实验

仿真场景由9个具有单位反射系数的点目标组成，在场景中心处有一点目标，其余8个点目标对称分布在以场景中心为圆心，半径为100m的圆上，雷达成像主要参数如表1所示。

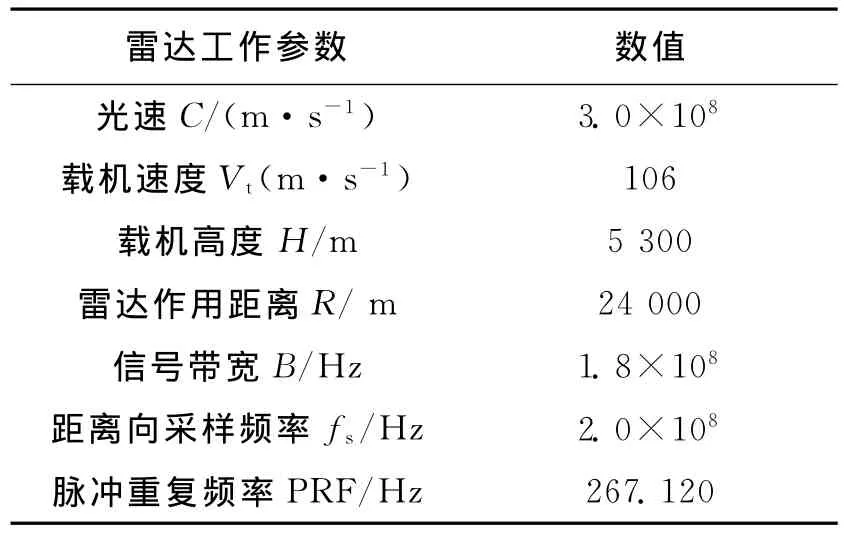
表1 雷达工作参数

首先采用极坐标格式算法（Polar format algorithm，PFA）在地平面对场景进行成像。该算法先对雷达回波数据分别进行方位向和距离向的插值处理，再通过在距离向和方位向分别作傅里叶变换，最终实现目标聚焦。插值后图像距离向分辨单元长度为0.668。仿真结果如图2所示。

根据图像分辨单元长度以及式（6）中所推导目标随自身高度在地平面的位移量，可以计算目标在图像中的理论偏移值

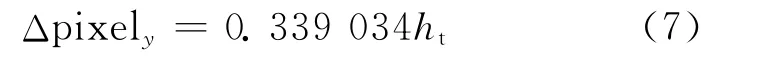
将其与实际仿真结果对比，如表2所示，发现所计算理论位置与实际仿真结果一致。

为了探究不同成像算法，不同成像平面，同一目标但自身高度不同的情况下，对目标偏移量的影响，在相同雷达工作参数下，选择Chirp Scaling算法（CSA），对改变各目标高度信息后的同一仿真场景在斜平面进行成像。该成像算法利用两维匹配滤波，实现目标聚焦。仿真结果如图3所示。

根据表1所示雷达工作参数，计算图像距离向分辨单元长度pixely为

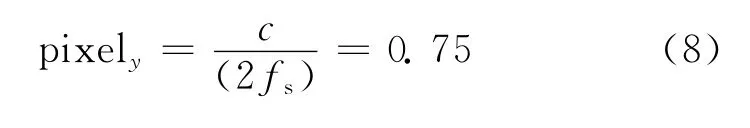
图2 PFA算法地平面成像

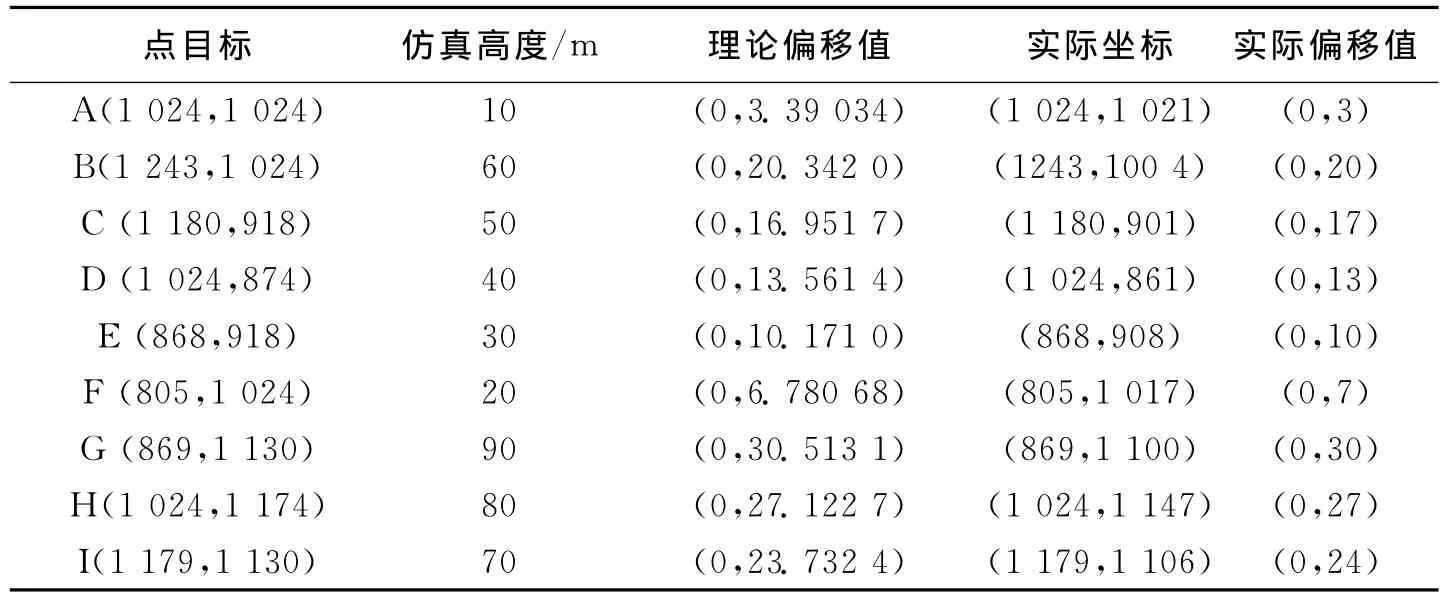
表2 PFA算法地平面成像点目标坐标

图3 CSA算法斜平面成像

根据式（5）中所推导目标随自身高度在斜平面的位移量，可以计算目标在图像中的理论偏移值

将其与实际仿真结果对比，如表3所示，发现所计算理论位置与实际仿真结果一致。说明目标随自身高度在图像中的位移量并不受成像算法的影响，仅与雷达成像几何及图像分辨单元大小有关，且正如本文所分析，目标在斜平面的偏移量就是该目标的地平面偏移量在斜平面的投影。不失一般性，在后续的理论分析和仿真实验中，仅分析和讨论利用PFA算法对目标场景在地平面进行成像。

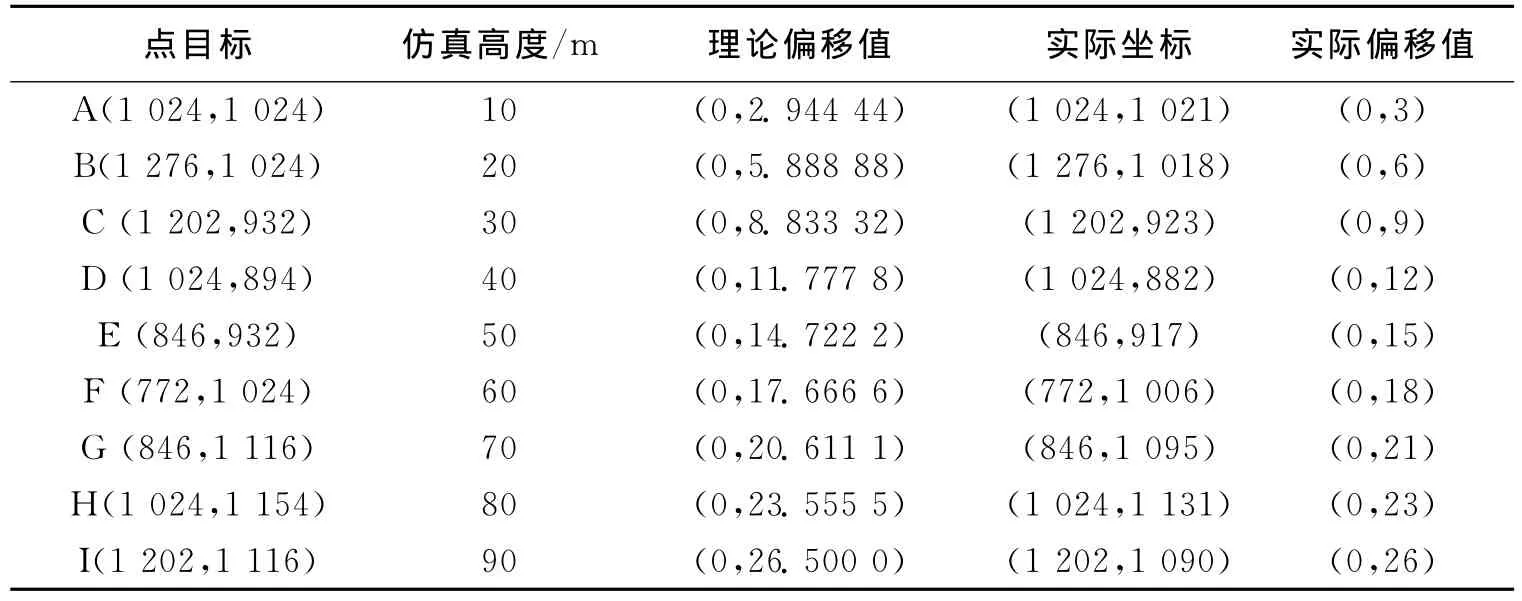
表3 CSA算法斜平面成像点目标坐标

2 斜视情况下的目标位置分析

在斜视情况下，假设载机沿X方向匀速直线运动，在地平面上定义垂直于载机方向为目标场景距离向Y。此时不同于正侧视情况，雷达视线所构成的斜平面与由载机运动方向所定义的目标场景方位向X存在夹角，目标投影至成像平面时，沿X，Y两个方向均存在一定的偏移。因此，在斜视情况下，不仅需要考虑目标自身高度对于目标成像位置在距离向上的影响，同时还要考虑其方位向的偏移。

2.1 理论分析

假设在位置S处，高度为H的雷达，与场景中心点O距离为R，其入射角为η，斜视角为φ。如图4（a）所示，雷达视线所构成的斜平面与场景方位向X，距离向Y的夹角分别为ηx和ηy。根据式（2），可以得到高度为ht的任意目标，在地平面沿场景方位向X和距离向Y的投影偏移量ΔRx和ΔRy

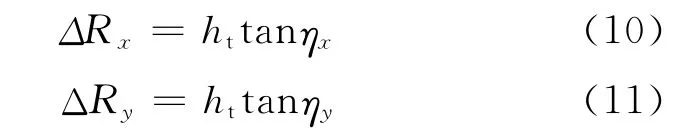
图4（b）为雷达成像几何在地平面的投影。定义雷达视线方向在地平面的投影Y′为图像距离向，垂直于该方向的X′为图像方位向。在斜视情况下，目标场景坐标系和图像坐标系之间夹角为φg。结合图4（a）和图4（b），有

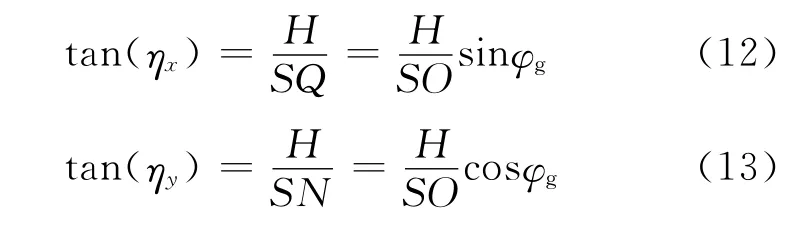
式中

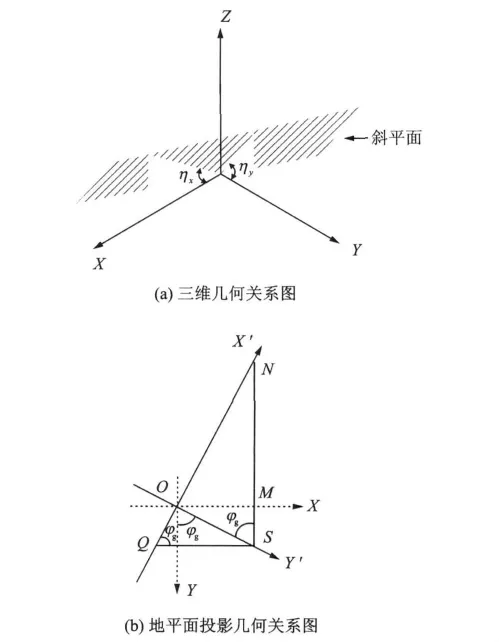
图4 斜视情况下雷达成像几何

利用式（16～17）中所示目标，由自身高度沿X，Y方向上的偏移量，确定目标在图像中的偏移范围，根据图5中所示几何关系，转换求得目标在图像坐标系中对应沿X′，Y′方向上的偏移量

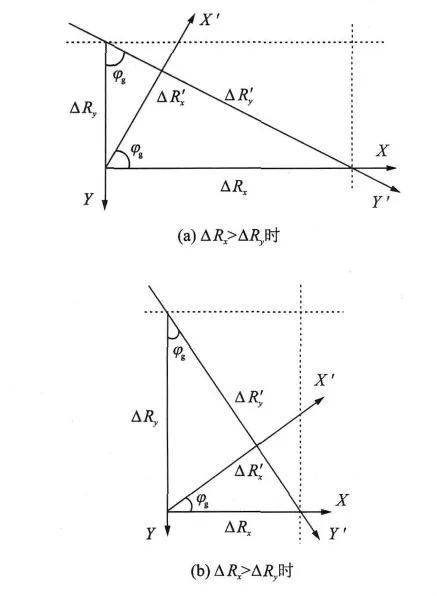
图5 目标位置偏移量转换几何关系

观察式（20～21），与正侧视情况下分析所得式（6）中结果一致。由于载机高度H，作用距离R和斜视角φ均已知，可以先利用InSAR处理估计得到目标的高度信息ht，再通过式（18～19），根据图像方位向和距离向的分辨单元长度，计算目标在图像中的位移量，准确定位目标真实位置所对应的像素单元。

2.2 仿真实验

图6 PFA算法地平面成像

观察图6（a），发现在斜视情况下，由于目标场景坐标系和图像坐标系之间存在夹角φg，所以图像相比较于图2（a）存在明显的旋转。在图6（b）中，可以看到目标因为自身高度，在方位向和距离向上均产生了明显位移。根据式（16～19），计算目标的理论偏移值

将其与仿真结果进行比较，如表4所示。仿真实验证明，本文分析理论偏移值与实验结果一致。

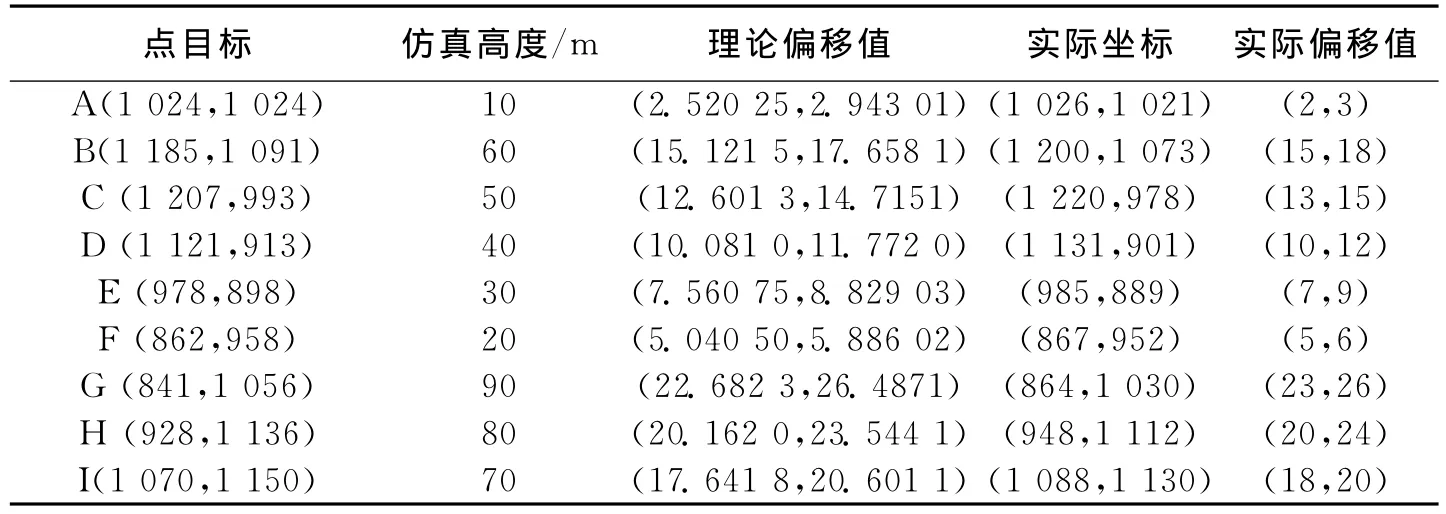
表4 PFA算法地平面成像点目标坐标

3 结束语

利用SAR干涉技术测量目标的高度信息，对目标场景进行三维成像时，目标会由于自身高度在图像上产生相应的位移，从而导致DEM中目标位置与实际观测场景中目标位置不一致。本文从正侧视情况出发，分析了目标随自身高度在图像中产生位移的原因，并从简单的正侧视情况推广到较为复杂的斜视情况，推导了目标在DEM中的位移量与成像几何，目标高度之间的数学关系，提供了正确定位目标位置的理论依据。通过仿真实验，验证了本文理论分析的正确性。

［1］ Jakowatz C J V，Daniel E W，Paul H E，et al.Spotlight mode synthetic aperture radar［M］.Boston：Kluwer Academic Publishers，1996.

［2］ Piotr Samczynski， Krzysztof S Kulpa.Coherent mapdrift technique ［J］.IEEE Trans on Geoscience and Remote Sensing，2010，48（3）：1505－1517.

［3］ Ryo Natsuaki，Akira Hirose.SPEC method－A fine coregistration method for SAR interferometry ［J］.IEEE Trans on Geoscience and Remote Sensing，2011，49（1）：1505－1517.

［4］ Curlander J C.Location of spaceborne SAR imagery［J］.IEEE Trans on Geoscience and Remote Sensing，1982，20（3）：359－364.

［5］ Carlos Lopez Martinez，Xavier Fabregas.Modeling and reduction of SAR interferometric phase noise in the wavelet domain［J］.IEEE Trans on Geoscience and Remote Sensing，2002，40（12）：2553－2566.

［6］ Liao Guisheng，Li Hai.Estimation method for In－SAR interferometric phase based on generalized correlation steering vector［J］.IEEE Trans on Aerospace and Electronic Systems，2010，46（3）：1389－1403.

［7］ Bian Yong，Mercer B.Interferometric SAR phase filtering in the wavelet domain using simultaneous detection and estimation ［J］.IEEE Trans on Geoscience and Remote Sensing，2011，49（4）：1396－1416.

［8］ Li Hai，Liao Guisheng.An estimation method for In－SAR interferometric phase based on MMSE criterion［J］.IEEE Trans on Geoscience and Remote Sensing，2010，48（3）：1457－1469.

［9］ 李海，吴仁彪.基于加权联合导向矢量模型的InSAR干涉相位估计［J］.数据采集与处理，2012，27（2）：131－137.Li Hai，Wu Renbiao.Estimation method for InSAR interferometric phase based on weight joint steering vector［J］.Journal of Data Acquisition and Processing，2012，27（2）：131－137.

［10］Wei Xu，Ian Cumming.A region growing algorithm for InSAR phase unwrapping ［J］.IEEE Trans on Geoscience and Remote Sensing，1999，37（1）：124－134.

［11］Mark D P，Jerome S S.Least－squares two－dimensional phase unwrapping using FFT′s ［J］.IEEE Trans on Geoscience and Remote Sensing，1994，32（3）：706－708.

［12］Zhong Heping，Tang Jinsong，Zhang Sen，et al.An improved quality－guided phase－unwrapping algorithm based on priority queue ［J］.IEEE Geoscience and Remote Sensing Letters，2011，8（2）：364－368.

［13］Yamaki Ryo， Hirose Akria.Singularty－spreading phase unwrapping ［J］.IEEE Trans on Geoscience and Remote Sensing，2007，45（10）：3240－3251.

［14］Zhang Kui，Ge Linlin，Hu Zhe.Phase unwrapping for very large interferometric data sets ［J］.IEEE Trans on Geoscience and Remote Sensing，2011，49（10）：3240－3251.

［15］宫记松，赵振宇，冯星，等.基于几何解析的双雷达地面目标定位算法［J］.数据采集与处理，2012，27（5）：620－624.Gong Jisong，Zhao Zhenyu，Feng Xing，et al.Location algorithm for ground target using twin－radar system based on geometry analytic method［J］.Journal of Data Acquisition and Processing，2012，27（5）：620－624.