最小冗余MIMO雷达阵列设计
洪振清 张剑云 梁 浩 游志刚
(合肥电子工程学院305教研室,合肥,230037)
引 言
为解决雷达目标RCS(Radar cross section)普遍存在的闪烁效应,近年来国际上提出了一种新型体制雷达——多输入多输出(Multiple-input multiple-output,MIMO)雷达[1],其基本思想是:在发射端采用多个发射天线同时发射正交信号照射目标,在接收端使用多个接收天线接收目标反射的回波信号,然后通过匹配滤波器组实现各路信号的分离。由于MIMO雷达的各个发射天线的发射信号彼此正交,因而能够在空间形成多个独立通道,从而增加系统 的 自 由 度[2](Degrees of freedom,DOF),改善空间目标的分辨率[3],有效地克服目标的RCS闪烁[4],提高系统的检测性能。MIMO雷达借鉴了在通信领域取得了巨大成功的多输入多输出技术,有着广泛的应用前景。
目前,对MIMO雷达的研究主要集中在目标检测、参数估计、成像和波形设计等方面,而 MIMO雷达的优化布阵是一个新的研究内容,相关的文献还非常少,值得进一步深入研究。与传统的天线阵列优化相比,MIMO雷达要综合考虑发射阵和接收阵,因而其阵列优化问题更加复杂。
文献[5]以波达方向估计精度为目标提出了一种MIMO雷达天线阵的设计方法,通过抛物线理论得出了收发组合的唯一性和合理性,然后通过分析各种收发组合给出了发射阵元的最佳间隔设置。文献[6]从目标散射模型、收发信号模型出发,提出了基于空间卷积理论的MIMO雷达天线阵列设计方法,着重分析和介绍了收发复用线性阵情况下的MIMO雷达阵列设计算法,给出并证明了其等效接收阵列存在的充要条件。文献[7]提出了一种基于遗传算法和禁忌搜索的混合二次优化布阵方法。该方法为了保证系统最大自由度,引入了距离扰动,同时对发射天线和接收天线的位置进行两次优化,有效解决了MIMO雷达天线方向图综合中低旁瓣电平设计问题。
文献[8]将最小冗余阵列的概念推广到 MIMO雷达,通过穷举法搜索得到最小冗余MIMO雷达的发射阵列和接收阵列的阵元位置,它可利用最少的物理阵元形成尽可能多的等效阵元,从而得到大的阵列孔径。但是,该文献并没有指出如何分配发射阵列和接收阵列,同时由于穷举法的运算复杂度往往很高,特别是在阵元数较多的情况下这种现象尤为严重,因此不利于实际应用。
本文在文献[8]的基础上,将最小冗余的思想与MIMO雷达虚拟阵元的概念相结合,利用组合设计理论中的循环差集的构造原理,提出一种新的最小冗余MIMO雷达阵列优化算法。该算法利用最少的物理阵元能够得到更大的阵列孔径,并且能快速解析地求出发射阵元和接收阵元的位置,克服了传统的穷举法运算复杂度高的不足,尤其是在大阵元数情况下其优势更加明显,因此本文算法具有更高的工程应用价值。
1 MIMO雷达信号模型
考虑发射阵和接收阵都是线性阵列的MIMO雷达,发射阵元数为M,接收阵元数为N,第m个发射阵元的位置关于半波长的归一化值为uT,m,第n个接收阵元的位置关于半波长的归一化值为uR,n。为描述方便,本文所提到的阵元位置均是指关于半波长的归一化位置。假设目标与发射阵列之间的距离远大于发射阵的阵列孔径,并且发射阵列和接收阵列之间的距离非常近(也可以是同一阵列),因此它们相对于目标的观测角相同。
MIMO雷达的发射阵同时发射M个窄带正交波形,第m个发射阵元的发射信号为sm(t),则整个发射信号矢量可以表示为S(t)=[s1(t),…,sM(t)]T,并且满足正交性条件∫T0S(t)SH(t)dt=IM,其中T0为雷达脉冲宽度,IM表示M×M的单位矩阵,符号(·)T和(·)H分别表示矩阵(或向量)的转置和共轭转置。假设空间某一远场目标的波达方向为θ,则N个接收阵元的输出信号矢量为
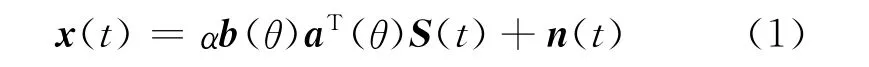
式中:x(t)为N×1维的接收信号向量,n(t)为N×1维的接收加性高斯噪声矢量,α表示目标回波的复振幅,a(θ),b(θ)分别为M×1维的发射导向矢量和N×1维的接收导向矢量,其表达式分别为

接收信号矢量经过MN个匹配滤波器后的输出为

式中=∫T0n(t)SH(t)dt。由于发射信号矢量S(t)满足正交性条件∫T0S(t)SH(t)dt=IM,所以对式(4)进一步化简,并对其进行矩阵的拉直操作后可得
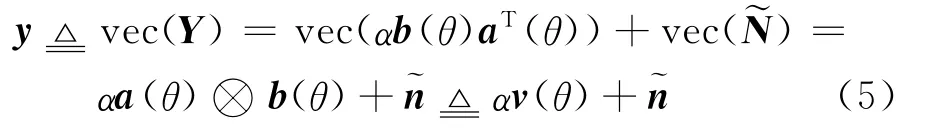
式中:y为MN×1维的匹配滤波器输出矢量为MN×1维的经过匹配滤波器后输出的噪声矢量,并假设方差为σ2的复白高斯过程,其协方差矩阵为Φ~n=σ2IMN,符号vec(·)表示矩阵拉直运算,⊗表示向量的 Kronecker积,v(θ)=a(θ)⊗b(θ)为MN×1维的MIMO雷达等效导向矢量。
由Kronecker积的定义和式(2,3)可知 MIMO雷达等效导向矢量v(θ)中有MN个元素,其中vmn(θ)=exp{jπ(uT,m+uR,n)sinθ},它等价于具有MN个阵元的虚拟阵列导向矢量[9],虚拟阵元的归一化位置为

式中k=1,2,…,NM。图1给出了发射阵元数M=3,接收阵元数N=4条件下的MIMO雷达阵列扩展示意图。

图1 MIMO雷达阵列扩展示意图
可以看出,M个发射阵元和N个接收阵元的MIMO雷达形成了MN个虚拟阵元,且实际的阵元个数越多,虚拟阵元的个数也就越多,相应的虚拟阵列孔径也就越大。因此,相对于传统的相控阵雷达,MIMO雷达的系统自由度更高,从而具有更窄的波束宽度和更高的角度分辨率。
2 最小冗余MIMO雷达
2.1 最小冗余阵列
Moffet[10]最早提出了最小冗余阵列的概念,其基本思想是在阵元间的位置差包含1到L(L为期望的归一化阵列孔径)之间的所有整数前提下,通过使阵元数M最小来降低系统硬件成本。如果以阵列的第一个阵元为参考点,即令u1=0,则阵元间相关函数只与阵元间的位置差di,j=ui-uj(其中1≤i,j≤M)有关。如果假设i≥j,亦即阵元间的位置差di,j是大于或者等于0的自然数,即所有阵元位置差的集合为

基于上述假设,最小冗余阵列的设计问题可以通过下面的约束优化问题来描述

式中|A|表示集合A的势。式(8)所描述的是一个组合优化问题,一般难于求解,但当L较小时,可以通过穷举法进行求解。表1给出了几种不同阵元数情况下最小冗余阵列的阵元位置[11](某一特定阵元数目的最小冗余阵的阵元位置不唯一,这里只列出其中一种)。

表1 最小冗余阵列
2.2 最小冗余MIMO雷达阵列
从前面的分析可知,MIMO雷达虚拟阵列的形成有效地扩展了阵列孔径,增大了整个系统的自由度。由于虚拟阵列的有效阵元数由虚拟阵列导向矢量中互不相等的元素个数决定,如果虚拟阵列导向矢量中出现相等的分量,则MIMO雷达虚拟阵列的有效阵元数就会减少,此时称虚拟阵列出现了冗余。因此可以将最小冗余的思想运用到MIMO雷达的阵列设计中,用最少的物理阵元形成尽可能大的阵列孔径,从而实现降低系统成本,提高系统性能的目的。
由式(6)可知,对于 MIMO雷达,其虚拟阵元的归一化位置为uT,m+uR,n,其中m=1,…,M;n=1,…,N,则所有虚拟阵元位置差的集合{uk-uk′}可以表示为
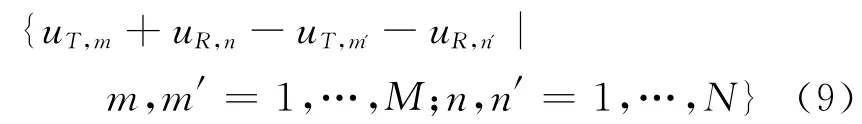
因此,最小冗余MIMO雷达的阵列设计问题可以通过下面的约束优化问题来描述

上式所描述的优化问题是比式(8)更为复杂的组合优化问题,当L较小时,可以通过穷举法进行求解,但是当L较大时,采用常规的穷举法运算复杂度会非常高。为了简化搜索,文献[8]作了如下简化

即将阵元位置差集合元素必须遍历所有1到L之间的所有整数约束条件简化为阵元位置差集合中的元素均为小于L的整数。然而,这种简化允许阵元位置差集合不连续,相当于否定了最小冗余概念中的遍历原则,得到的结果往往是次优的。同时,优化得到的阵元位置仅仅是M+N的最小时的收发阵元组合,而没有给出具体的发射阵和接收阵设置准则。
3 基于循环差集的MIMO雷达阵列优化
3.1 差集和循环差集的定义
差集和循环差集是组合设计理论中的重要概念,这里只给出其基本定义[12,13],其详细理论可以参考文献[14]。
定义1 对给定的正整数P,存在k个整数所组成的集合A={a1,a2,…,ak},满足下列两个条件(1)0=a1<a2<…<ak=P;(2)任意整数p(0≤p≤P)均可表示为集合A中两元素的差,则称集合A为P上的受限差集(简称差集),记为A(P,k)。
课外阅读,离不开教材选文学习示范。对教材选篇有效处理,学生掌握不同文本阅读方法。分析教材选文,不是“学生根据教师的指令在课文里找表面的信息”,而是使学生明白诗歌阅读是通过对字词的理解走向诗人情感、散文阅读从句子中理解作者独特情感、小说阅读在于谋篇布局与细节等具体阅读方法。针对同文体中不同文本,教会学生不同的阅读方法,形成多样化阅读能力。学习《套中人》,学生能掌握阅读《群魔》《小公务员之死》等反映现实小说的阅读方法。阅读示范包括环境示范。文学理论认为:阅读是读者与作者、作品、世界的对话。阅读对话需要安静环境。每周语文课或语文晚自习安排学生安静阅读的时间。
定义2 以正整数V为模的K个互不同余的整数所组成的集合,记为D={d1,d2,…,dK},如果对任一整数v(0<v<V),恰好在D中有Λ个有序对(di,dj),使得等式v≡(di-dj)(modV)成立,其中modV表示对V求模,则称该集合为一个(V,K,Λ)循环差集,记为D(V,K,Λ)。
循环差集的各参数之间满足如下关系

因此,循环差集的3个参数中只有两个参数是独立的。对于任意满足式(12)的(V,K,Λ),可能不存在差集,也可能一组或多组差集。特别地,当Λ=1时,D(V,K,Λ)称为完备循环差集,因为差集表中非零元素(1,2,…,V-1)出现且仅出现一次。对于完备循环差集,有[13]

此时V恒为奇数。
3.2 基于循环差集的最小冗余MIMO雷达阵列设计算法
如果把循环差集D(V,K,Λ)中的V看成是阵列关于半波长的归一化孔径,K看成阵元个数,Λ看成是阵元间位置差的出现次数,则由3.1节的分析可知,完备循环差集D(V,K,1)恰好对应最优最小冗余阵列。
考虑到最小冗余MIMO雷达要求其虚拟阵元的位置差能遍历所有小于L的整数,可以先设定发射阵列为最小冗余阵,使发射阵列的阵元位置差满足连续无间断的要求,然后再优化接收阵列,使系统形成的虚拟阵元位置差满足式(10)中的约束条件。因此,可以得到基于循环差集的最小冗余MIMO雷达阵列设计算法步骤如下:
(1)设定发射阵元数初始值M=3和接收阵元数上限Nmax;
(2)将发射阵列设置为最小冗余阵列,得到发射阵元的位置{uT,m},由前面的分析可知,集合{uT,m}是一个循环差集D(VT,M,ΛT);
(3)设定接收阵元数初始值N=3;
(4)设{bn}是对应阵元数N时的最小冗余阵列的阵元位置,显然集合{bn}也是一个循环差集D(VR,N,ΛR),取 接 收 阵 元 的 位 置 为 {uR,n}={VT·bn};
(5)根据发射和接收阵元位置计算虚拟阵列的阵元位置差,判断其是否遍历1到L之间的所有整数,如果是,转到(7),否则,进入下一步;
(6)判断接收阵元数N>Nmax是否成立,如果成立,M=M+1,转到(2),否则,N=N+1,转到(4);
(7)综合发射阵元和接收阵元的位置,得到最小冗余MIMO雷达。
最小冗余MIMO雷达阵列设计算法的流程图如图2所示。
4 仿真结果及分析
为了便于分析,主要考虑MIMO雷达的发射阵元数为M=3,接收阵元数为N=5的情形,分别比较本文算法得到的最小冗余MIMO雷达、文献[8]算法得到的最小冗余MIMO雷达和均匀线阵MIMO雷达的性能,其中均匀线阵MIMO雷达发射阵元间距为λ/2,接收阵元间距为Mλ/2。
4.1 阵列扩展性能验证
本实验比较本文算法和文献[8]算法的阵列扩展性能。由文献[8]算法计算出发射阵元的位置为{uT,m}={0,1,3},而接收阵元的位置为{uR,n}={0,6,13,40,60},则相应的虚拟阵元位置为{0,1,3,6,7,9,13,14,16,40,41,43,60,61,63},虚拟阵列的归一化孔径为L=63。按本文算法可以计算出发射阵元的位置为{uT,m}={0,1,3},该集合是一个参数为(7,3,1)的循环差集,从表1中可以看出,N=5对应的最小冗余阵列阵元位置为{bn}={0,1,4,7,9},因此,可以求得接收阵元的位置为{uR,n}={0,1,4,7,9}×7={0,7,28,49,63},则虚拟阵元的位置为{0,1,3,7,8,10,28,29,31,49,50,52,63,64,66},虚拟阵列的归一化孔径为L=66。显然,本文算法所得到的最小冗余MIMO雷达阵列孔径要大于文献[8]算法。图3给出了两种算法所得到的最小冗余MIMO雷达的虚拟阵元位置差的直方图,其中纵坐标重复数表示具有相同阵元位置差的重复阵元对个数。

图2 阵列设计算法流程图
从图3可以看出,本文算法所得到的最小冗余MIMO雷达的虚拟阵元位置差遍历了所有1到66之间的整数,而文献[8]算法所得到的最小冗余MIMO雷达的虚拟阵元的位置差遍历了所有1到63之间的整数。值得说明的是,本文算法得到的最小冗余MIMO雷达孔径优势会随着阵元数的增大而逐渐增加。
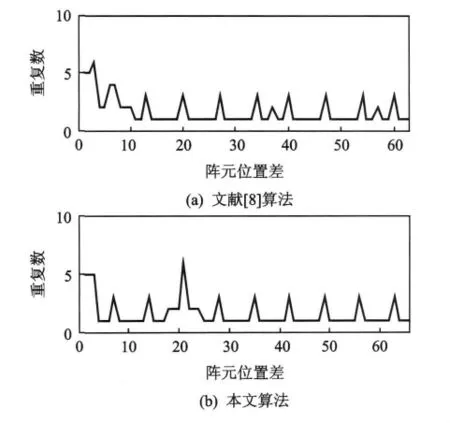
图3 最小冗余MIMO雷达的虚拟阵元的位置差
4.2 波束形成性能比较
假定期望目标的到达方向(DOA)为0°,信噪比0dB,空间有3个干扰目标,其DOA分别为-60°,2°,15°,干噪比分别为10,10,20dB,快拍数为K=200。图4为3种MIMO雷达的MVDR波束形成器的方向图。图5为3种MIMO雷达的MVDR波束形成器的输出信干噪比(SINR)与信噪比(SNR)的关系图,其中每个取值点进行500次独立的Monte-Carlo实验。

图4 3种MIMO雷达的MVDR波束方向图
从图4可以看出,对于-60°和15°方向的旁瓣干扰,3种MIMO雷达都能在这两个方向形成零陷,从而有效地进行抑制;对于2°方向的主瓣干扰,均匀线阵MIMO雷达的波束方向图出现了主瓣分裂,不能进行抑制,而最小冗余MIMO雷达仍然能够有效地抑制。这是因为与均匀线阵MIMO雷达相比,最小冗余MIMO雷达的虚拟阵列孔径更大,因而具有更窄的主瓣宽度。由图5可知,文献[8]算法得到的最小冗余 MIMO雷达的输出SINR要比均匀线阵MIMO雷达的输出SINR高5dB,本文算法得到的最小冗余MIMO雷达的输出SINR要比文献[8]算法得到的最小冗余MIMO雷达的输出SINR高约1dB,这是由于本文算法得到的最小冗余MIMO雷达的虚拟阵列孔径稍大于文献[8]算法得到的最小冗余MIMO雷达的虚拟阵列孔径。
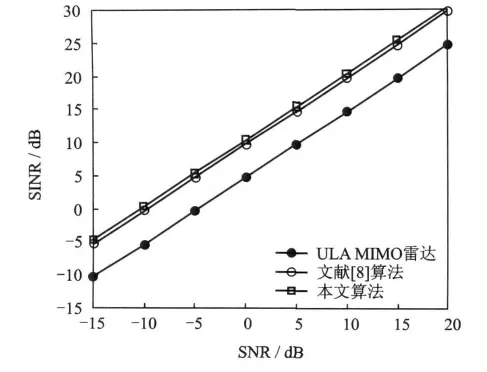
图5 3种MIMO雷达的输出SINR
4.3 角度分辨率比较
假设两个目标的DOA为θ1=-2°和θ2=2°,发射信号采用频率扩展信号[15],快拍数为K=200。如果则称θ1和θ2这两个目标可分辨。进行500次独立的Monte-Carlo实验,图6,7分别为3种MIMO雷达的分辨概率和角度估计均方根误差(RMSE)随SNR的变化关系图。
由图6可以看出,本文算法得到的最小冗余MIMO雷达的分辨概率和文献[8]算法得到的最小冗余MIMO雷达的分辨概率相当,两者均高于均匀线阵MIMO雷达的分辨概率。最小冗余MIMO雷达的分辨概率在SNR为-16dB时达到100%,而均匀线阵MIMO雷达的分辨概率要在SNR为-8dB时才达到100%。图7显示本文算法和文献[8]算法得到的最小冗余MIMO雷达的角度估计RMSE相同,在低信噪比的情况下,最小冗余MIMO雷达的角度估计RMSE要小于均匀线阵MIMO雷达,在高信噪比的情况下,最小冗余MIMO雷达和均匀线阵MIMO雷达的角度估计RMSE趋于一致。图6和图7表明最小冗余MIMO雷达的角度分辨率要高于均匀线阵MIMO雷达,这与虚拟阵列孔径越大,角度分辨率越高的理论相符。

图6 3种MIMO雷达的分辨概率
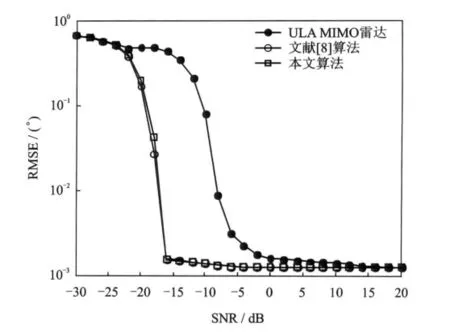
图7 3种MIMO雷达的角度估计均方根误差
5 结束语
本文将最小冗余的思想与MIMO雷达虚拟阵元的概念相结合,利用组合设计理论中的循环差集的基本原理,提出了一种基于循环差集的最小冗余MIMO雷达阵列设计算法。该算法利用最少的物理阵元能够得到更大的阵列孔径,并且能迅速确定发射阵元和接收阵元的位置,克服了传统的穷举法运算复杂度高的不足,因此本文算法更具有工程应用价值。通过计算机仿真,验证了本文所提出的算法的有效性。
[1] Fishler E,Haimovich A,Blum R,et al.MIMO radar:an idea whose time has come[C]//Proceedings of the IEEE Radar Conference.Philadelphia,PA:[s.n.],2004:71-78.
[2] Bliss D W,Forsythe K W.Multiple-input multipleoutput(MIMO)radar and imaging:degrees of freedom and resolution[C]//Proc 37th Asilomar Con Signals,Systems,Computers.Pacific Grove,CA:[s.n.],2003:54-59.
[3] Bekkerman I,Tabrikian J.Target detection and localization using MIMO radars and sonars[J].IEEE Transactions on Signal Processing,2006,54(10):3873-3883.
[4] Fishler E,Haimovich A,Blum R S,et al.Spatial diversity in radars-models and detection performance[J].IEEE Transactions on Signal Processing,2006,54(3):823-838.
[5] 陆珉,许红波,朱宇涛,等.MIMO雷达DOA估计阵列设计[J].航空学报,2010,31(7):1410-1416.Lu Min,Xu Hongbo,Zhu Yutao,et al.Array design of MIMO radar estimation of DOA[J].ACTA Aeronautic et Astronautica Sinica,2010,31(7):1410-1416.
[6] 粟毅,朱宇涛,郁文贤,等.多通道雷达天线阵列的设计理论与算法[J].中国科学:信息科学,2010,40(10):1372-1383.Su Yi,Zhu Yutao,Yu Wenxian,et al.Multi-channel radar antenna array design theory and algorithms[J].Science in China:Information Sciences,2010,40(10):1372-1383.
[7] 和洁,冯大政,李晓明.基于遗传算法和禁忌搜索的MIMO雷达天线布阵优化[J].数据采集与处理,2011,26(4):413-419.He Jie,Feng Dazheng,Li Xiaoming.Optimization of antenna array geometry in mimo radar based on genetic algorithm and tabu search[J].Journal of Data Acquisition and Processing,2011,26(4):413-419
[8] Chen C Y,Vaidyanathan P P.Minimum redundancy MIMO radars[C]//Proceedings of IEEE International Symposium on Circuits and Systems(ISCAS).Se-attle,WA:[s.n.],2008:45-48.
[9] Robey F C,Coutts S,Weikle D,et al.MIMO radar theory and experimental results[C]//Proc 38th Asilomar Conf Signals,Systems,Computers.Pacific Grove,CA:[s.n.],2004:300-304.
[10]Moffet A T.Minimum-redundancy linear arrays[J].IEEE Transactions on Antennas and Propagation,1968,16(2):172-175.
[11]王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社,2004.Wang Yongliang,Chen Hui,Peng Yingning,et al.Theory and algorithms of spatial spectrum estimation[M].Beijing:Tsinghua University Press,2004.
[12]Dong J,Li Q X,Guo W.A combinatorial method for antenna array design in minimum redundancy MIMO radars[J].IEEE Antennas and Wireless Propagation Letters,2009,8:1150-1153.
[13]董健,李青侠,靳榕,等.基于差集的综合孔径圆环天线阵稀疏优化方法[J].微波学报,2009,25(6):27-31.Dong Jian,Li Qinxia,Jin Rong,et al.Difference set based methods for optimal thinned circular arrays in aperture synthesis radiometers[J].Journal of Microwaves,2009,25(6):27-31.
[14]沈灏.组合设计理论[M].上海:上海交通大学出版社,1996.Shen Hao.Combinatorial design theory[M].Shanghai:Shanghai Jiaotong University Press,1996.
[15]He Q,Blum R S,Godrich H,et al.Target velocity estimation and antenna placement for MIMO radar with widely separated antennas[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(1):79-100.

