适用于任意雷达航迹的双基PFA波前弯曲误差补偿

何成宇 毛新华

（南京航空航天大学电子信息工程学院，南京，210016）

引 言

双基SAR系统中发射机和接收机分置于不同的平台，因此与单基SAR系统相比，双基SAR的操作方式更为灵活，获取的信息也更为丰富；而且通过采用远距离发射、近距离接收的工作方式可以使雷达作用距离更远，安全性和抗干扰性能更好。凭借上述优势，双基SAR成像成为近年来雷达领域研究的热点问题之一。

相比于单基SAR，双基SAR无论是系统实现还是成像信号处理都要复杂得多。就成像信号处理而言，双基SAR成像的主要难点在于：（1）距离历程具有双根式性，这使得基于驻留相位原理的回波信号频谱推导变得非常困难；（2）双基SAR成像几何具有三维特性，这导致很多单基SAR成像算法无法直接推广应用于双基SAR。尽管如此，科研工作者们还是提出了很多行之有效的成像算法。如基于单站转换的DMO（Dip－moveout）算法［1］，该算法通过对双基SAR回波数据进行预处理，将其转换为等效的单基SAR回波数据，进而利用单基SAR算法进行成像处理。基于显式频谱近似的LBF（Loffeld′s bistatic formula）［2］和 MSR（Multiscale retinex）方法［3］，其中 LBF方法通过将发射和接收引起的相位在各自的驻定相位点进行泰勒展开并保留到二次项来计算目标频谱，而MSR通过将回波相位表示成多项式形式并计算出各项系数获得目标频谱。基于隐式频谱分解的成像算法，如 Giroux 算 法［4］、Ender算法［5］和 QIU 算 法［6］。这些算法在双基SAR移不变模式下具有很好的应用前景，但却很难推广应用于更具实用价值的移变模式。目前，能够应用于双基移变模式的成像算法主要有卷积反投影算法［7－8］和双基PFA［9－11］。但卷积反投影算法属于时域算法，计算效率非常低，目前要达到实时处理还存在困难。而双基PFA虽然效率较高，但存在平面波前假设，其聚焦成像场景范围受到限制。

为了扩大双基PFA聚焦成像场景范围，文献［9］将单基PFA波前弯曲误差补偿方法［12］推广应用到双基SAR，提出了双基PFA波前弯曲误差补偿方法。但该方法在进行波前弯曲误差补偿时的空间频域滤波器的设计要求雷达平台飞行轨迹必须是线性的，因此无法将其推广应用于任意航迹条件下的成像处理。

本文提出了一种新的空变后处理方法，该方法通过对相位历史域的波前弯曲误差函数做与双基PFA成像相同的极坐标格式转换处理，得到雷达任意航迹条件下波前弯曲误差在两维空间频域的精确表示即一个空间频域滤波器，再通过分块后滤波处理去除散焦现象，最后通过图像域的重采样校正几何失真实现波前弯曲误差补偿，能够有效提高聚焦成像场景范围。

1 双基SAR信号模型

图1是双基聚束SAR的数据采集几何模型。不失一般性，假设发射机和接收机均以任意航迹飞行。以地面成像场景中心为坐标系原点、地平面为xy平面建立坐标系。在给定任意方位时刻t，发射机的瞬时方位角及俯仰角和接收机的瞬时方位角及俯仰角分别记为φt（t），θt（t）和φr（t），θr（t），发射机和接收机到场景中心的瞬时距离分别记为Rtc（t）和Rrc（t）。又假设场景中有一点目标，其位置为（xm，ym），发射机和接收机到该目标的瞬时距离记为Rt（t）和Rr（t）。

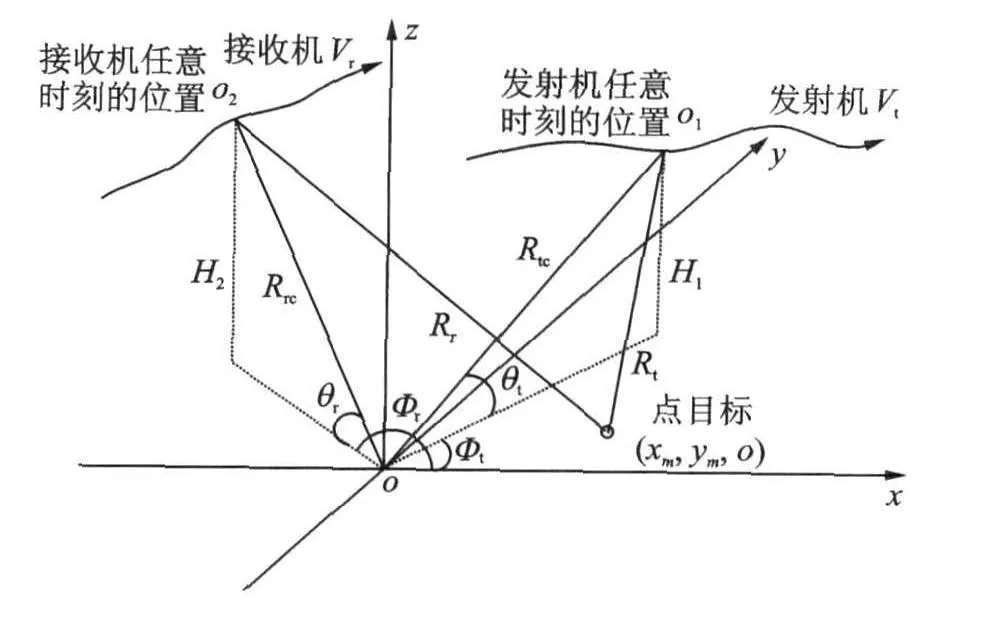
图1 双基SAR数据采集几何模型

假设雷达发射一个载频为fc的宽带信号，则场景中点目标的回波信号经过解调、匹配滤波和运动补偿后可以表示为［9］

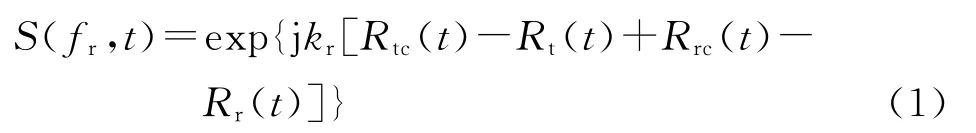
式中：kr＝2π（fc＋fr）／c，fr为距离频率，c为电磁波传播速度，为简化表示，式中忽略了幅度效应。

2 双基PFA

根据图1所示几何关系，并采用平面波前假设，式（1）中的差分距离可近似表示为［9］

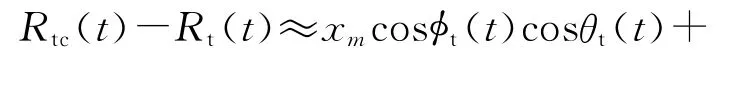
式（5）表明，雷达回波信号经过适当预处理后（即前面提到的解调、匹配滤波和运动补偿），可以看成是雷达波束照射场景函数傅里叶变换域的两维离散采样。因此，理论上通过对式（5）做两维逆离散傅里叶变换（DFT），即可得到目标的图像。

实际实现时，为了提高计算效率，总是希望能够利用快速傅里叶变换（FFT）来实现DFT。而要利用FFT实现两维逆DFT，必须要求信号在两维频域（即（kx，ky）域）是均匀采样。通常，雷达录取到的数据在（fr，t）域是采样均匀，但通过式（4）映射到（kx，ky）域后，采样位置却是按极坐标格式存放。因此在利用两维FFT成像前，必须对式（3）所示两维信号进行重采样，即改变信号在（fr，t）域上的采样位置，使重采样后的信号在（kx，ky）域是采样均匀的，这一过程通常称为极坐标格式转换。

通过极坐标格式转换后，式（5）所示信号可表示为

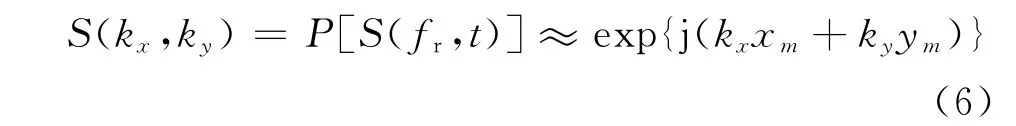
式中P［·］表示极坐标格式转换操作，其具体实现可参考文献［9］。

最后，对式（6）所示信号进行两维FFT即可得到目标的聚焦图像

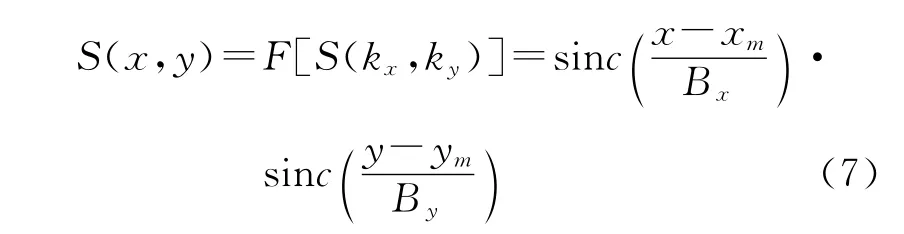
式中F［·］表示两维FFT，Bx和By分别为目标在x和y方向的频谱宽度。

3 波前弯曲误差分析

本文对差分距离进行了一阶近似，即采用了平面波前假设，实际的雷达波前是球面波前，由此引入的误差将限制双基PFA的有效成像范围。对波前弯曲误差进行补偿是扩大双基PFA成像范围的有效途径。而波前弯曲误差的补偿建立在波前弯曲误差分析的基础上，因此首先对双基PFA波前弯曲误差进行分析。

在实际的球面波前条件下，式（1）所示回波信号可以分解成如下两部分

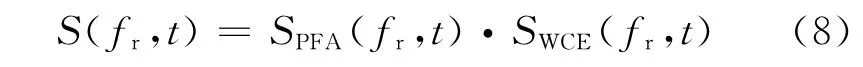
式中SPFA（fr，t）＝exp｛jφPFA（fr，t）｝为双基PFA 所依赖的基本成像项，而

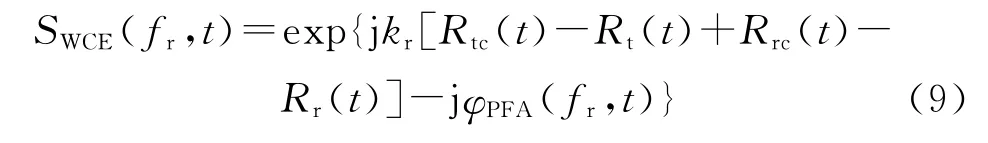
为双基PFA所不希望的波前弯曲误差项。

基于空变后处理的波前弯曲误差补偿方法通过构造一个二维空间频域滤波器来去除波前弯曲误差效应，因此获得波前弯曲误差在两维空间频域的表示是这种补偿方法实现的关键。式（9）只是波前弯曲误差在相位历史域的表示，因此问题的关键在于如何利用SWCE（fr，t）得到两维空间频域的波前弯曲误差项。已有方法都是利用泰勒展开得到波前弯曲在两维空间频域的近似表示，而且这些方法都依赖于雷达线性运动假设，无法推广到任意雷达航迹。

在极坐标格式算法中，相位历史域到两维空间频域的转换通过极坐标格式转换完成

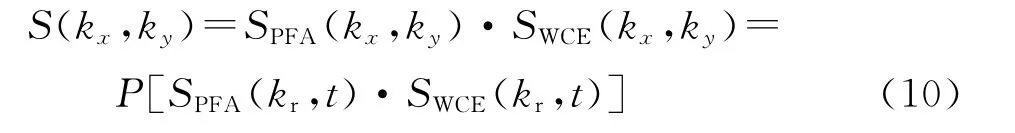
式中SWCE（kx，ky）为两维空间频域的波前弯曲误差。

极坐标格式转换是对信号的一个两维插值操作，在满足奈奎斯特采样定理前提下，它具有保运算特性，即它满足

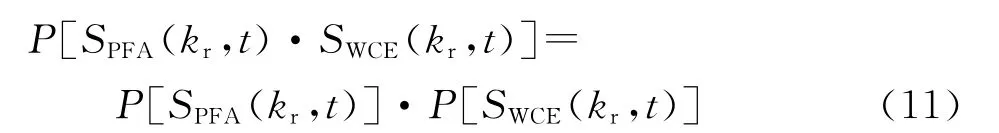
可以看到，与利用傅里叶变换将信号从相位历史域变换到二维空间频域不同，相位历史域中基本成像项和误差项的乘积在通过极坐标格式转换变换到二维空间频域后，恰好等于两个信号分别作极坐标格式转换后的乘积，因此波前弯曲误差项的二维空间频域表示SWCE（kx，ky）可以通过对相位历史域的波前弯曲误差项SWCE（kr，t）作与粗聚焦成像完全相同的极坐标格式转换来得到，即

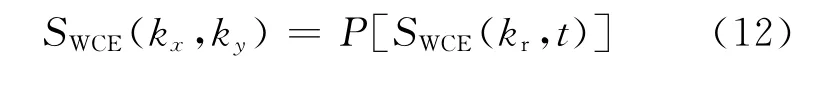
4 波前弯曲误差补偿

基于式（12）所示波前弯曲误差表示，本文提出了一种基于空变后处理的双基SAR极坐标格式算法波前弯曲误差补偿方法，其处理流程如图2所示。主要步骤包括空变滤波和几何失真校正两部分。

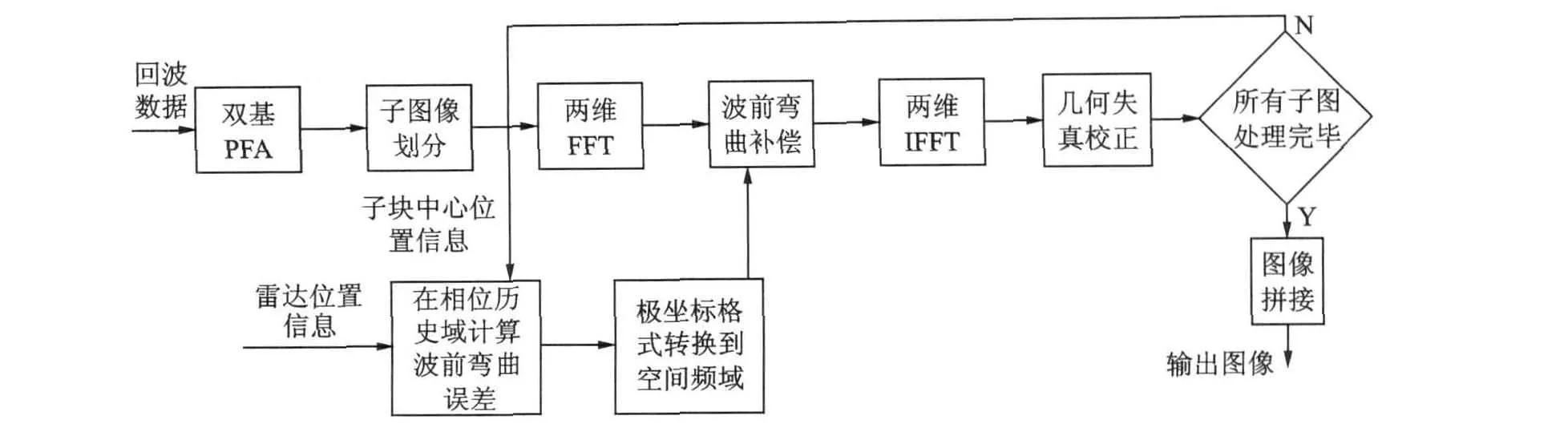
图2 波前弯曲误差补偿处理流程图

4.1 空变滤波

由于波前弯曲误差具有空变性，即不同位置的目标具有不同的波前弯曲误差，因此没有办法统一补偿，空变后处理方法通过对双基PFA粗聚焦图像进行分块校正来解决误差的空变补偿问题。子块图像大小的选择要保证子块内波前弯曲误差散焦效应的空变性可以忽略，但几何失真的空变性允许存在，这是因为波前弯曲导致的图像几何失真空变性要比散焦的空变性更严重，选取更小的子块固然可以使几何失真的空变性也能忽略，但会由于子块数过多导致算法效率降低。然后，对每个子块图像，根据子图中心位置信息得到相位历史域的波前弯曲误差表示，再通过一个极坐标格式转换将其转换到二维空间频域即式（10）中SWCE（kx，ky），然后对其取共轭构造一个二维空间频域滤波器。接着对子块图像进行二维FFT变换到二维空间频域，经过二维空间频域滤波器滤波后，作二维IFFT变换回图像域，得到滤波后的子图像。由于补偿前子块内目标散焦空变性可以忽略，因此补偿后所有目标都得到精确聚焦。

4.2 几何失真校正与子图拼接

虽然子块内目标散焦空变性可以忽略，但除子块中心点外，其余目标仍存在几何失真，而且双基PFA粗聚焦图像也存在几何失真，因此在目标精确聚焦后、子块拼接前还必须对子块图像进行几何失真校正。

因为雷达平台高机动主要引入高频误差，所以几何失真映射关系仍可根据理想线性航迹得到，根据文献［9］得到的图像像素单元位置与实际空间位置的几何失真映射关系，对子块作一个二维插值，就可以使子块图像得到精确的几何失真校正。

对各个子块图像分别进行上述波前弯曲误差补偿后，再将所有补偿后子块图像进行无缝拼接即可得到整个场景的高分辨聚焦图像。

5 仿真数据处理

利用X波段SAR仿真回波数据对算法进行了验证。仿真系统主要参数如下：雷达发射信号中心频率10GHz，带宽600MHz，距离向和方位向分辨率均为0.25m。数据采集几何模型如图1所示，发射机孔径中心时刻到场景中心距离Rtc（0）为3 500m，发射机孔径中心时刻的俯仰角为16°，方位角为45°。接收机孔径中心时刻到场景中心距离Rrc（0）为3 500m，接收机孔径中心时刻的俯仰角为19°，方位角为30°。设置地面仿真点目标分布如图3所示，相邻点目标距离向距离为180m，方位向距离为240m。

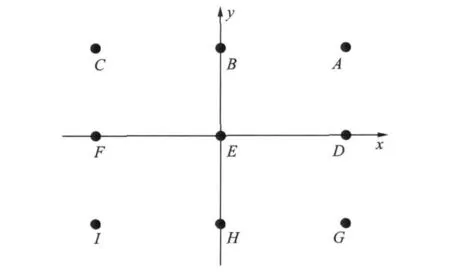
图3 地面点目标分布图

为验证算法在任意航迹下的波前弯曲误差补偿性能，假设雷达平台在y和z方向有高频扰动，发射机和接收机扰动大小分别如图4和图5所示。

图6为整个场景区域9个点目标双基PFA粗聚焦成像的仿真处理结果，从图中可以明显看出，双基PFA粗聚焦成像结果中的9个点目标除中心点外都存在几何失真和散焦。图7为粗聚焦图像经过本文的波前弯曲补偿算法补偿后的聚焦图像，可以看到场景区域的点目标都得到了精确聚焦和几何失真校正（由于双基原因图像坐标系有个旋转）。

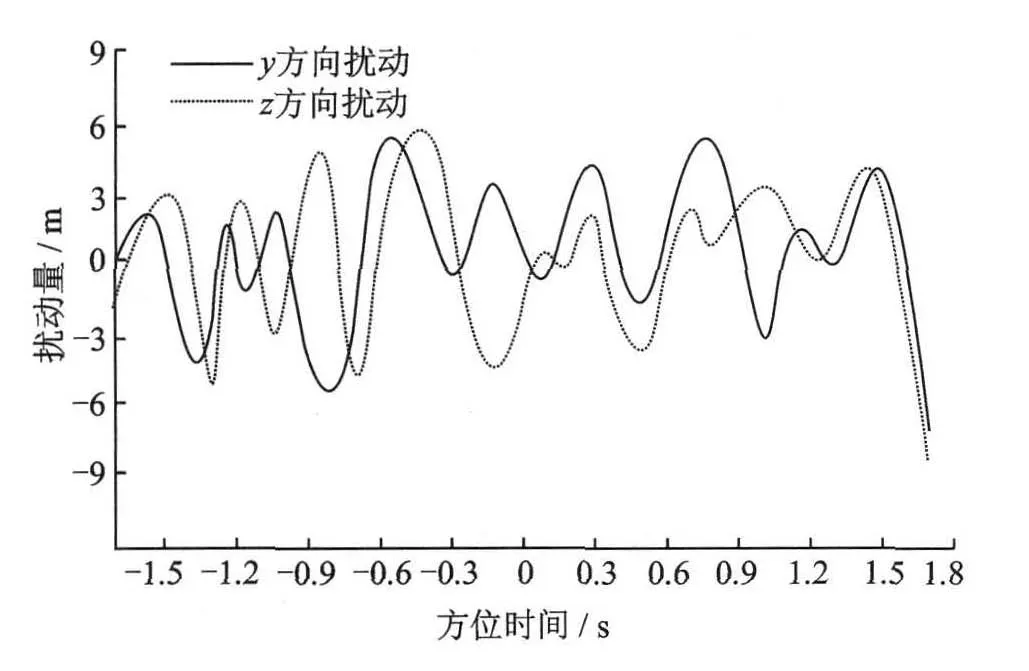
图4 雷达发射机平台扰动

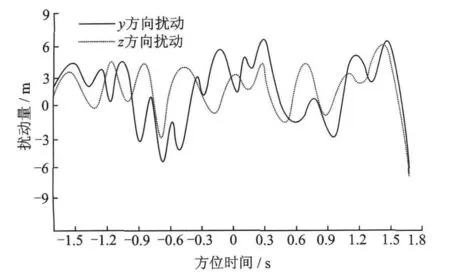
图5 雷达接收机平台扰动

图6 双基PFA成像处理结果

以A，B，D，E这4个有代表性的点目标为例，从几何失真和聚焦精度两方面给出本文补偿方法仿真处理结果的详细分析。表1给出了该算法对这4个点目标的定位结果。从表1中可以看到，双基PFA粗聚焦成像结果中的4个点目标除中心点外都明显偏离了其真实位置，因此图像存在较大的几何失真。而通过本文方法对波前弯曲误差进行补偿后，在测量精度范围内，目标定位结果与其真实位置基本吻合。

图7 波前弯曲补偿后结果

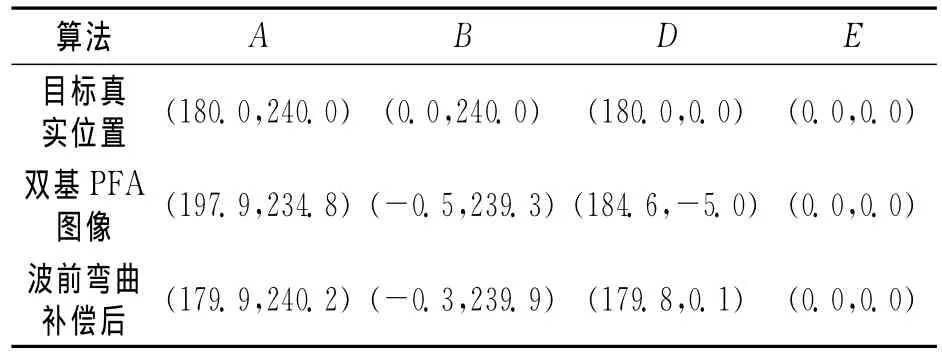
表1 几何定位结果 m

图8给出了A，B，D，E4个点目标在波前弯曲补偿前后的二维响应图（为了细化旁瓣结构，图像在距离和方位向都进行了16倍的重采样）。从图中可以看到，受波前弯曲误差影响，除了靠近场景中心的部分目标外，其余目标均存在明显的散焦，通过本文方法进行波前弯曲补偿后，所有目标聚焦效果都接近理想，波前弯曲效应得到明显补偿。

图8 波前弯曲补偿前后点目标二维响应图

6 结束语

本文提出了一种双基SAR极坐标格式算法波前弯曲误差补偿方法，该方法在相位历史域计算波前弯曲误差并将其通过极坐标格式转换变换到两维空间频域进行补偿，有效地解决了雷达平台高机动任意航迹条件下的波前弯曲误差补偿问题。仿真结果表明，即使在雷达航迹存在高频扰动条件下，本文方法仍能对大场景进行精确聚焦成像。随着成像分辨率的提高，合成孔径时间增长，雷达平台非线性运动将不可避免，因此本文算法在双基SAR大场景超高分辨率成像时具有很大的应用前景。

［1］ Hale D.Dip－moveout by Fourier transform［J］.Geophysics，1984，49：741－757.

［2］ Chen S C，Wu Q S，Zhou P，et al.Precision analysis of loffeld′s bistatic formula for constant－offset case［R］.National Lab of Radar Signal Processing.Xi′an：Xidian University，2012.

［3］ Jobson D J，Rahman Z，Woodell G A.A multi－scale Retinex for bridging the gap between color images and the human observation of scenes［J］.IEEE Transactions on Image Processing：Special Issue on Color Processing，1997，6：965－976.

［4］ Giroux V，Cantalloube H，Daout F.An Omega－K algorithm for SAR bistatic system［J］.Proceedings of IGARSS，2005，2：1060－1063.

［5］ Ender J.A step to bistatic SAR processing［C］／／European Conference on Synthetic Aperture Radar（EUSAR′04）.Ulm，Germany：［s.n.］，2004：359－363.

［6］ Qiu X L，Hu D H，Ding C B.An Omega－K algorithm with phase error compensation for bistatic SAR of a translational invariant case［J］.IEEE Transactions on Geoscience and Remote Sensing，2008，46（8）：2224－2232.

［7］ Carrara W G，Goodman R S，Majewski R M.Spotlight synthetic aperture radar：signal processing algorithms［M］.Boston：Artech House，1995.

［8］ Loffeld O，Nives H，Peters V.Models and useful relations for bistatic SAR processing［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42（10）：2031－2038.

［9］ Wang X，Zhu D Y.Wavefront curvature correction in one stationary bistatic SAR image focused via PFA［J］.IET Electronics Letters，2010，46（18）：1291－1293.

［10］Rigling B D，Moses R L.Polar format algorithm for bistatic SAR［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，40（4）：1147－1159.

［11］夏玉立，黄瑶，雷宏.双站聚束SAR极坐标格式成像算法［J］.数据采集与处理，2009，24（1）：49－54.Xia Yuli，Huang Yao，Lei Hong.Polar format algorithm for bistatic spotlight SAR［J］.Journal of Data Acquisition and Processing，2009，24（1）：49－54.

［12］毛新华，朱岱寅，叶少华，等.一种基于图像后处理的极坐标格式算法波前弯曲补偿方法［J］.电子学报，2010，38（1）：244－250.Mao Xinhua，Zhu Daiyin，Ye Shaohua，et al.Image domain space variant post－processing for wavefront curvature correction in polar format spotlight SAR image［J］.Acta Electronica Sinica，2010，38（1）：244－250.