模糊多目标规划在建设项目决策中的应用

郑 欢，程 周

（1.四川大学工商管理学院不确定实验室，成都 610064；2.重庆工商大学管理学院，重庆 400067）

0 引言

现有的项目决策模型只考虑到直接成本，包括人工、材料、机械设备和其他直接关系到项目活动的费用，忽视了相关间接成本，包括利息、管理、折旧、合同违约金及其他可变成本。在实际情况下，一个项目的总成本是在项目计划水平之上直接成本和间接成本的总和，一般情况下，项目管理决策致力于项目完成时间和项目总成本的最小化。因此，项目决策者可能会通过增加直接费用来加快项目进程以达到缩短完成时间实现间接费节约的目标。

本文目的在于建立了一个两阶段模糊规划方法来解决不确定环境下多个模糊目标的项目管理决策问题。文章多目标线性规划模型在考虑了直接成本、间接成本、合同处罚成本、活动持续时间和预算限额的条件下同时最小化项目总成本、总工期和总压缩成本。

1 模型及算法

模糊多目标决策问题的研究可以描述如下，假设一个项目包括n个相关的活动，且必须以一定的顺序来完成整个任务。因为有些环境系数和参数在项目计划阶段是不完整的，所以项目决策的目标函数不能被精确衡量。本文试图建立一个两阶段模糊目标规划方法来优化每项活动的持续时间和压缩时间，并同时考虑到直接成本、间接的成本和可用的预算限额。模糊多目标线性规划模型试图同时最小化项目总成本、总完成时间和总压缩成本。

1.1 假设条件

（1）目标函数在不确定期望水平上是模糊的。

（2）目标函数和约束条件是线性的方程。

（3）直接成本从正常值到压缩值随活动完成时间呈线性增加。

（4）每一活动的正常完成时间和压缩时间，正常成本和压缩成本都是确定的。

（5）在计划水平上可用总预算是可知的。

（6）模糊目标采用线性隶属度函数，最小算子和平均算子被循环用于加权模糊集。

（7）总间接成本可以分为固定成本及可变成本,单位时间的可变成本不随完成时间变化。

1.2 模糊线性规划目标函数

项目经理必须在一定资源条件下同时实现多目标管理，即同时考虑最小化项目总成本、完成时间、压缩成本，而这些目标通常是模糊不确定的。

1.3 约束条件

（1）活动i,j的时间约束：

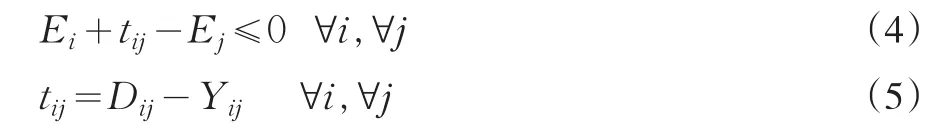
（2）活动i,j的压缩时间约束：

（3）总成本预算约束：

1.4 模型求解

阶段1：最小算子法。在阶段1中，最初的模糊多目标决策模型可以通过Bellman和Zadeh(1970)的模糊决策理念解得。首先，各个模糊函数的正理想解（positive ideal solution，PIS）和负理想解(negative ideal solution,NIS)描述如下：

相应的模糊目标函数的可能值区间是基于决策者的经验和知识来估计的，等价隶属度区间为[0,1]。

最小算子用以加权模糊集。引入满意度变动辅助函数L(1)，将模糊多目标线性规划问题转化为等价的普通线性模型，单目标线性规划模型可以表示为：

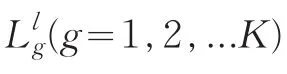
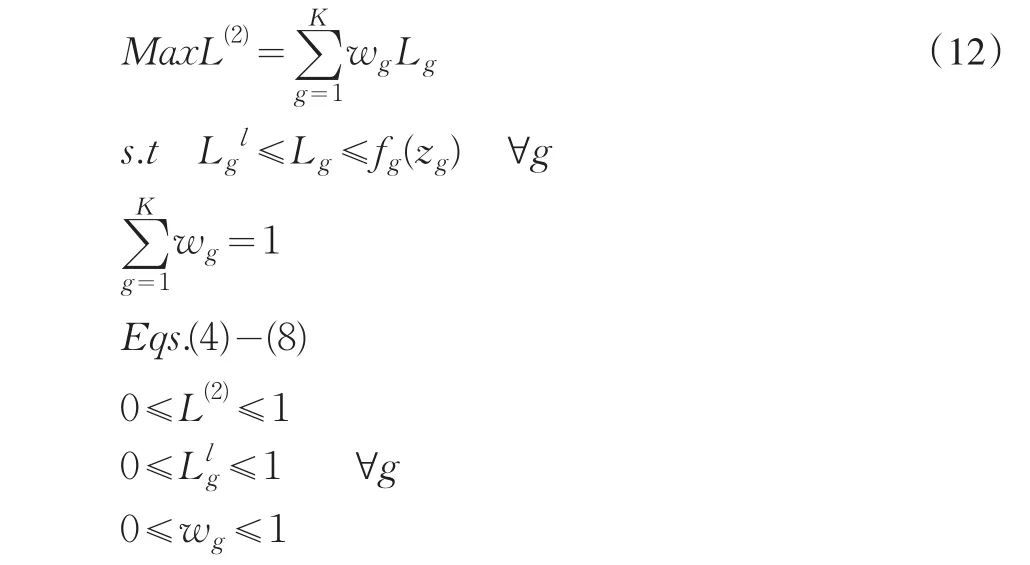
其中，wg(g=1,2,…K)是决策者对几个目标函数各自的偏好。在实际工程项目管理决策中，各目标权重的变化和最低限度值如模型（12）。

2 案例分析

本案例用两阶段模糊规划方法来求出项目管理计划，解决在不确定环境下的房地产开发建设项目中的管理决策问题。通过对整个项目决策过程的分析，来论证该方法的实用性。

2.1 项目介绍

金科·世界城，位于重庆茶园新区商业金融核心地段，项目总体规划为街区商业、居住、生活配套等多功能为一体的城市综合体。总建筑面积约34万㎡。

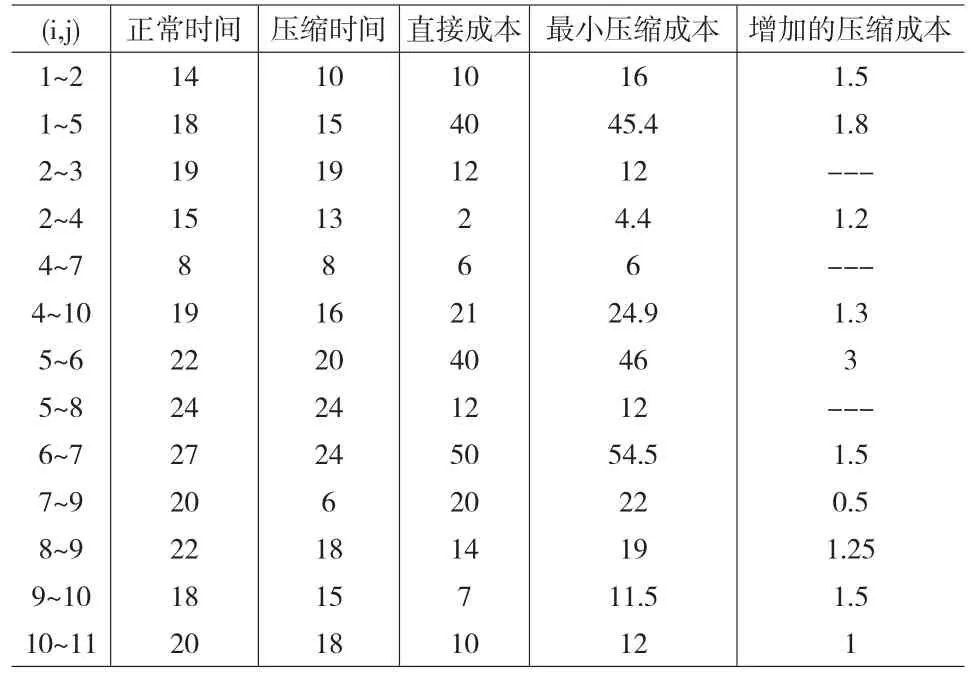
表1 世界城案例中计划工作的相关数据 （时间单位：天；成本单位：万元）

由于世界城规模庞大，为分析方便，本案例将其中一栋商业项目作为研究对象。表1列举了本案例的基本数据。其他相关数据如下：固定的间接成本120万元，节约的日常变动成本1.5万元，总预算385万元，正常条件下项目完成时间125天。项目开始时间为0。关键路径是1-5-6-7-9-10-11。网络计划图如图1：

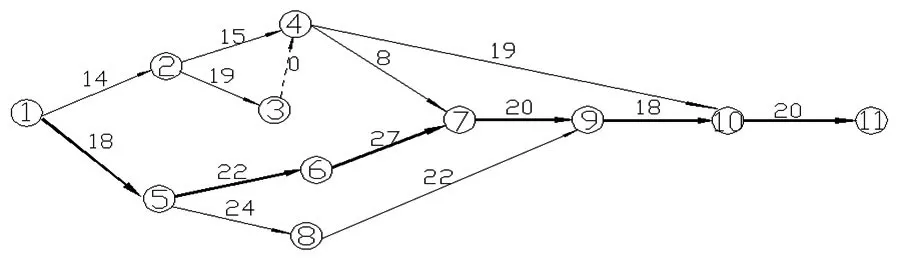
图1 网络计划图

2.2 计算程序

世界城案例应用两阶段模糊多目标规线性划方法来解决模糊决策问题的解决程序如下。在阶段1，根据Eqs.(1)～(8)列出所要解决问题的模糊多目标线性规划模型。通过Eqs.(9)的目标函数的PIS和NIS，结果如下：

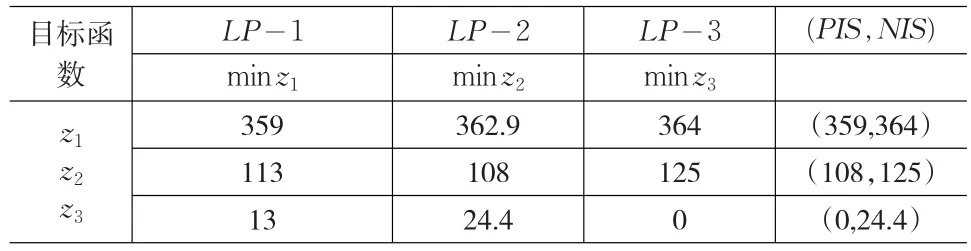
表2 各目标函数的的PIS和NIS

表2列出了普通线性规划模型的最优解以及每个模糊目标的(PIS,NIS)。

因此，通过Eqs.(10)，每个模糊目标函数的非增连续线性隶属度函数如下：

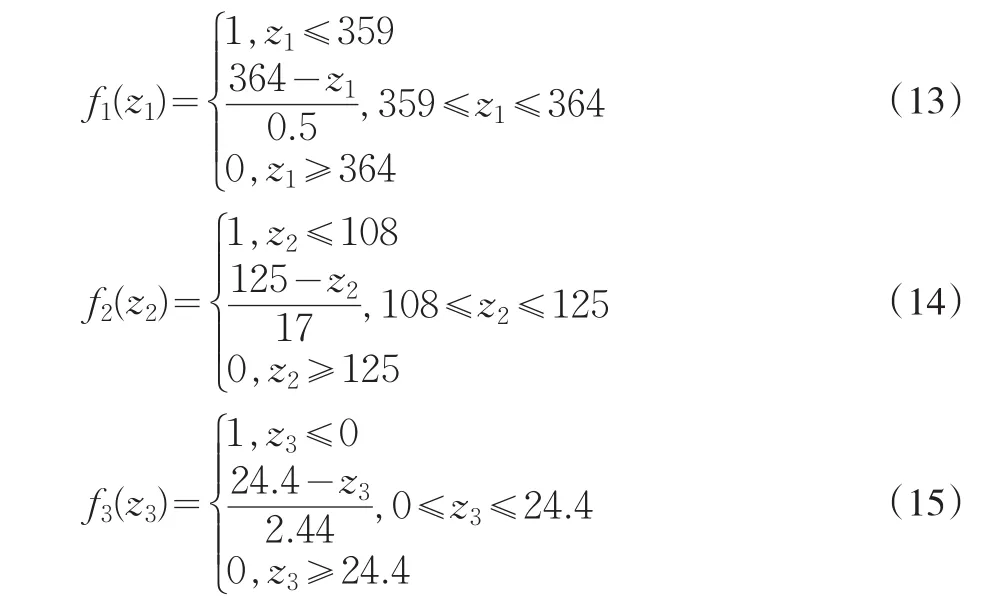
表3 项目计划的最初方案和改进方案

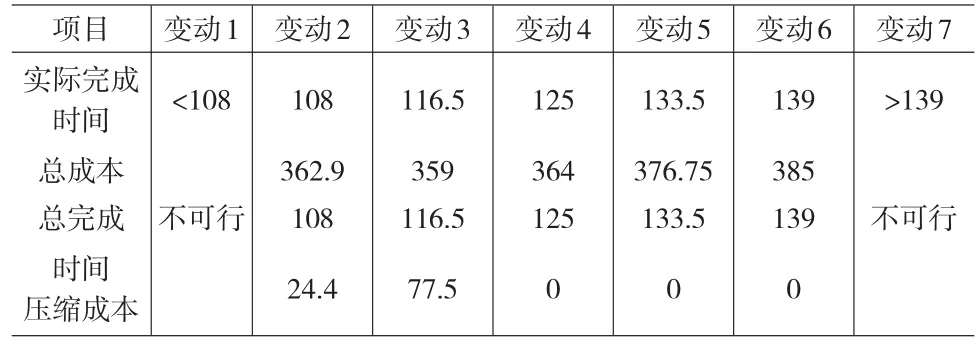
表4 完成时间的敏感性分析

期望完成时间的敏感度分析也被用于该案例的分析中，如表4。不同项目工期的敏感性分析结果表明，最小化完成时间与最小化项目总成本和最小化压缩成本是相互矛盾的，如图2所示。当项目持续时间远远低于108天时项目是不可实行的，因为关键线路上所有活动的累计压缩时间超过了允许的上限17天。反之，如果项目完成时间延长到139天以外,由于总成本超过了可用预算，也是不可行的。因此，可以通过缩短工期来实现间接费用的节约、增加直接费来加快项目。如果项目经理因为项目完成时间的推迟而面对高额的间接费用和合同索赔，那么通过额外资源的使用来减少项目完成时间就显得更有意义，因为它可以在一定程度上降低费用总额。

以项目总成本、总完成时间和总压缩成本三个参数为分析指标。由于工期长，条件多变，完成时间最容易受其他因素影响，是最不稳定的参数，因此选取完成时间为不确定性因素。由于完成时间在108天到139天范围内变动，假定变动率为0.7，得出的各参数的变动值如表4所示。从图2可以很明显的看出，在完成时间不确定、同样变动率的条件下，项目的压缩成本是最为敏感的因素，在决策前，应对项目计划工期做出预计，合理安排各工序的工作时间，保证实际工期在计划范围内，以减少压缩成本对项目完成时间的影响。

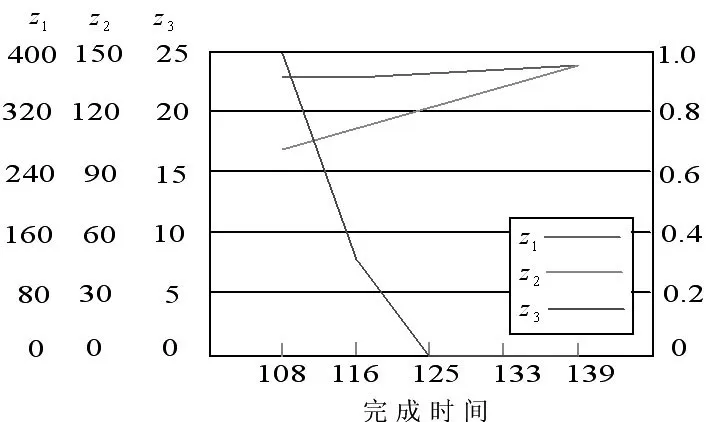
图2 分析完成时间敏感性的目标值

2.3 计算分析与对比

将两阶段模糊目标规划模型应用于项目决策问题中得到如下重要性质。首先，如表3所显示的，经过两阶段模糊目标规划并应用了加权平均算子加总模糊集的决策过程得到的解总会比阶段1最小算子得到的解效率提高。表3中的数据也说明了本文提出的方法获得的解明显优于一阶段最小算子法，因此，所提出有效解决方法能够提供改进的使决策者满意的项目管理方法。

第二，所提出的方法包含了一个解决多目标项目管理问题的模糊决策过程。两阶段模糊目标规划法可以为模糊多目标项目管理提供一个已知的综合满意度值。如果整体的项目决策满意度为L=1，那么每个目标都是完全满意，如果是0＜L＜1，所有目标在L水平上是满意的，如果L=0，则没有一个目标是满意的。一般来说，如果决策者没有接受最初的总体满意值，L值可能通过调整来适应一个更好的决策结果。例如，世界城案例中最初的一阶段决策满意度0.5892。重新获得的L值是决策者为了寻找一个更好的解决方案而调整的，经过改进的高效的结果为项目总成本359.786万元，总完成时间110.38天，总压缩成本17.72万元，整体决策者满意度提高到0.7359。

第三，由于计划期信息不完全和不确定，所以项目管理中的多个目标为模糊的，这些相互冲突的目标在不确定水平下必须同时优化。表4和图2显示了几个目标之间的平衡关系。从案例分析结果可知，提出的方法能很好满足模糊环境下多目标的实际应用。

3 结束语

本文的多目标线性规划模型，在考虑直接成本、间接成本、合同处罚成本和现有预算情况下,力求同时最小化总成本、总完工时间和总压缩成本。用一个案例的实施情况来证明应用两阶段模糊的目标规划方法解决项目决策问题的可行性。本文的贡献在于创建了一个两阶段模糊数学规划方法来解决多目标的模糊项目管理决策问题，并提供了一个有利于决策者交互的调整搜索方向直到找到最优解的系统决策框架。

本文局限性在于模糊目标函数和相关可用资源约束中涉及的每单位时间成本系数假设为确定。因此，该方法应改进来使它更好的使用于实践中。此外，该方法呈现了决策问题中线性隶属度函数的模糊目标。将来的研究者也可能应用分段线性、非线性的相关隶属函数来建立模糊多目标项目决策模型。

[1]Lukaszewicz,J.On the Estimation of Errors Introduce by Standard As⁃sumptions Concerning the Distribution of Activity Duration in PERT Calculations[J].Operations Research,1965,（13）.

[2]Parks,W.J.,Ramsing,K.D.The Use of the Compound Poisson in PERT[J].Management Science,1969,(15).

[3]Chanas,S.,Kamburowsi,J.The Use of Fuzzy Variable in PERT[J].Fuzzy Sets and Systems,1981,(5).

[4]Mjelde,K.M.Fuzzy Resource Allocation[J].Fuzzy Sets and Systems,1986,(19).

[5]Chang,I.S.,Tsujimuta,Y.,Gen,M.,Tozawa,T.An Efficient Ap⁃proach for large Project Planning based on Fuzzy Delphi Method[J].Fuzzy Sets and Systems,1995,(76).

[6]DePorter,E.L.,Ellis,K.P.Optimization of Project Network Problem with Goal Programming and Fuzzy Linear Programming[J].Computers and Industrial Engineering,1990,(19).

[7]Arikan,F.,Gungor,Z.An Application of Fuzzy Goal Programming to a Multiobjective Project Network Problem[J].Fuzzy Sets and Systems,2001,(119).

[8]Wang,R.C.,Liang,T.F.Project Management Decisions with Multiple Fuzzy Goals[J].Construction Management and Economics,2004,(22).

[9]Wang,R.C.,Liang,T.F.Application of Multiple Fuzzy Goals Program⁃ming to Project Management Decisions[J].International Journal of In⁃dustrial Engineering-Theory,Applications,and Practice,2006,(13).