部分线性变系数模型的Backfitting约束估计

安佰玲,魏传华

(1.淮北师范大学 数学科学学院，安徽 淮北 235000；2.中央民族大学 理学院,北京 100081)

0 引言

作为变系数模型和部分线性模型的推广,部分线性变系数模型在近年来得到了广泛的研究.该模型可记为如下的形式

其中Y是因变量,(U,xT,zT)为对应的自变量,不失一般性,下面假定U 为一维变量,β=(β1,β2,…,βq)T为q维未知待估参数,α(⋅)=(α1(⋅),α2(⋅),…αp(⋅))T为一列未知函数。 ε为模型误差,有 E(ε)=0 和 Var(ε)=σ2。

针对模型(1),已有多种方法提出用以估计其中的未知参数β。文[1]基于局部多项式估计方法最早研究了模型(1),文[2]利用小波方法估计该模型。文[3]针对该模型提出了一种新的有效估计,文[4]研究了模型的级数估计,文[5]提出了Profile最小二乘估计并且基于广义似然比检验方法研究了该模型的检验问题,文[6]研究了参数分量的Backfitting估计。

实际问题研究中,我们经常要对回归模型的参数(待估模型系数)向量有附加的约束条件,比如生产和消费问题的研究,详细的讨论可参见文[7]。对于一般的线性回归模型,我们都知道在约束条件下有约束最小二乘估计.然而对于半参数模型来说,关于约束条件下模型的推断问题的研究非常少。文[8]基于Profile最小二乘方法和Backfitting方法分别讨论了部分线性模型的约束估计问题。文[9]基于Profile最小二乘方法研究了模型(1)的约束估计问题并提出了一种profile拉格郎日乘子检验方法.作为文[8][9]中结果的推广，本文要研究的是模型(1)在附有约束条件下的Backfitting估计问题.我们考虑如下线性约束条件

Aβ=b

其中 A为k×q的已知矩阵,且rank(A)=k,b为k×1已知向量。

1 模型的Backfitting估计

在构造约束估计之前,我们先介绍文[6]针对模型(1)提出的Backfitting估计方法。假设

2 模型的Backfitting约束估计

下面我们考虑线性约束Aβ=b下模型(2)的估计问题。基于模型(2)以及约束条件,构造辅助函数

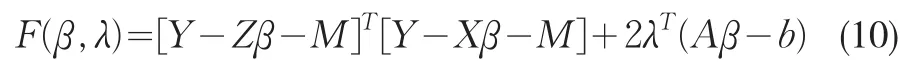
其中λ为k维Lagrange乘子。假定变系数部分M已知,将函数 F(β,λ)分别对 β,λ求导,并令偏导数等于0,有下面的估计方程

将上式带入(13)式得β的约束估计为

3 约束条件的检验

本节我们考虑约束条件的Aβ=b的存在性,即考虑如下的假设检验问题

众所周知,线性回归模型的推断中,对于上面的假设检验问题,主要是基于比较原假设和背择假设下的残差平方和的思想构造检验统计量.下面我们也基于此思想来构造检验统计量.首先我们有当H0成立时,即约束条件Aβ=b成立时,模型(2)基于上一节所提估计方法的残差平方和为

其中λ1=tr(M0-M1),δ1=tr(M1)显然检验统计量T的分子RSS0-RSS1反映了原假设与备择假设下模型的拟合效果的差异。若二者有显著差异，则倾向于拒绝原假设H0。因此,大的T值趋于拒绝原假设H0。由于模型拟合的复杂性,检验统计量T在原假设下一般不服从F分布,不过我们可以在模型误差为正态分布的假定下用F逼近法求其检验 p值。利用文[10]中的结果,令t为T的观测值,则检验p-值有如下结论

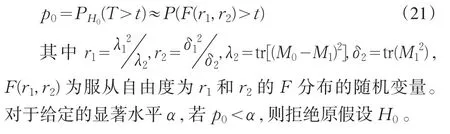
[1]Zhang,W.,Lee,S.,Song,X.Local Polynomial Fitting in Semivary⁃ing-Coefficient Model[J].J.Multivar.Anal,2002,82(1).

[2]Zhou,X.,You,J.Wavelet Estimation in Varying Coefficient Partially linear Regression Models[J].Statist.Probab.Lett,2004,(68).

[3]Xia,Y.C.,Zhang,W.Y.,Tong,H.Efficient Estimation for Semivary⁃ing-Coefficient Models[J].Biometrika,2004,(91).

[4]Ahmad,I.,Leelahanon,S.,Li,Q.Efficient Estimation of Semiparamet⁃ric Partially linear Varying Coefficient Model[J].Ann.Statist,2005,(33).

[5]Fan,J.,Huang,T.Profile likelihood Inferences on Semiparametric Varying-coefficient Partially linear Models[J].Bernoulli,2005,(11).

[6]魏传华,吴喜之.部分线性变系数模型Backfitting估计的渐近性质[J].高校应用数学学报,2008,23(2).

[7]Jorgenson,D.W.Econometric Modeling of Producer behvaior[M].Cambridge：MIT Press,2000.

[8]Przystalski,M.,Krajewski,P.Constrained Estimators of Treatment Pa⁃rameters in Semiparametric Models[J].Statistics&Probability Letters,2007,(77).

[9]魏传华,吴喜之.部分线性变系数模型的profile拉格郎日乘子检验[J].系统科学与数学,2008,28(4).

[10]Cleveland,W.S.Robust locally Weighted Regression and Smoothing Scatterplots[J].Journal of the American Statistical Association,1979,(74).