路网增长引导的区域经济扩散度量方法

王 琳，于 洋，陈钢铁

（西南交通大学a.交通运输与物流学院；b.建筑学院，成都610031）

0 引言

目前，有关交通路网的研究成果众多[1～2]，主要研究角度和方法体现在：一是立足宏观尺度，采用数量经济学方法，度量路网变化引起的宏观经济和社会效应，提出由此引起的产业集聚策略；二是采用微观视角，以特定区域为背景，对特定时间断面上的经济社会发展指标与运输网络特征指标数据进行统计分析，运用可达性等评价指标，研究运输网络特征变化引起的经济社会空间布局的结构特征。上述成果为运输网络对区域经济格局的影响提供了较为完善的研究范式，但是二者互馈关系的复杂性，以及我国路网建设长期滞后、规划引导性明显增强的特点，使得相关研究亟需在理念和方法上有所创新。本文采用能够较好反映我国当前运输网络发展新形势的“交通引导发展”理念，以区域经济和区域路网为背景，研究区域单核心城市的多经济体在路网规划引导下向周边城镇扩散的过程，尝试提供一种度量受交通条件影响的经济扩散效应的模型和算法。

1 研究假设

区域内的城镇分布是区域经济体集聚和扩散的地理空间载体，因而区域经济体的分布数量和形式呈现多样化的特征。选择具有单一核心城市、多中小城镇的区域作为研究起步，便于作为区域经济空间格局的基础形式，向多核心城市的区域拓展。

区域经济体在地理空间的分布一般呈现聚集和分散两种形式。通常，区域间运输通道的构建会引起经济体在区域内核心城市的集聚效应，而区域路网的增长则主要引起经济体在区域内部的扩散效应。以区域内部的经济扩散效应为对象，以多经济体已在核心城市形成的聚集作为初始分布状态，研究其在路网规划的引导下，向区域内部选择性扩散的过程，符合区域内部路网与经济空间扩张的客观规律。

与需求增长的渐进性不同，路网建设具有平台性，即在建成后相对较长的一段时期内基础设施能力基本维持稳定。多经济体扩散形成的运输需求的稳步增长，与路网规划所提供的运输能力的阶段增长之间存在阶段均衡的现象，为规避这种客观情况所带来的循环效应，选择以阶段性路网规划形成为起始，以多经济体扩散后形成稳态为终止，以达到扩散稳态所需的时间最短为优化目标，可以形成合理的分析周期。

各经济体在扩散过程中会不断调整自身的扩散速率和方向，受企业发展规划、企业间信息不对称、运输的距离效应和扩散路径容量等因素的影响，各经济体的扩散呈现出不同的规律和相互影响的动态关系，通过经济体的扩散组合、扩散速度、扩散路径的长度和其上的经济体密度等变量来体现该动态过程。

2 模型建立

2.1 主要变量

（1）区域经济扩散网络：定义阶段性区域路网规划所形成的运输网络G(S，A)，其中S={s1,s2,……,sn}为有限节点集合，A为有限弧集合，A⊆S×S。s1,s2,……,sn为区域规划路网中的节点（城镇）集合，s1为经济体的扩散起点，即区域的核心城市，si为经济体的扩散路径的中间点或终点，即区域规划路网所衔接的其他城镇。

（2）扩散路段长度：lij为区域规划路网中节点si,sj,(si,sj)∈A之间的距离；

（3）路段扩散速度：vij为区域规划路网中节点si,sj,(si,sj)∈A之间路径上经济体的扩散速度，表达式如（4）所示；

（4）路段扩散时间：tij表示经济体从节点si扩散到sj所需要的时间；ti为经济体到达扩散路径(si,sj)上的节点si时刻，tj为经济体到达扩散路径(si,sj)上的节点sj时刻，有tij=tj-ti；

（5）决策变量：xij=0或1，其中xij=1表示弧(si,sj)在选定的扩散路径上；xij=0表示弧(si,sj)不在选定的扩散路径上；

（6）扩散路径：扩散路径P定义为从扩散起点到扩散目的节点的一条有效路径，P为网络中结点的有序序列，设pk为路径P中包含的各结点在网络中的编号，则路径P可用 (sp1,sp2,……,spk)表示，其中 1≤pk≤n，k 是结点 spk在路径P中的经过顺序编号。p1=1,pk=n，即路径P起始于扩散起点，终止于扩散目的节点。考虑到经济扩散效应的周期划分，扩散路径P应可行且不包含回路。

（7）路径扩散时间：沿路径p=(sp1,sp2,……,spk)，1≤pk≤n，由结点sp1至结点spk所用的时间定义为沿路径p扩散至结点spk的扩散时间，记作ET(P,spk)，有

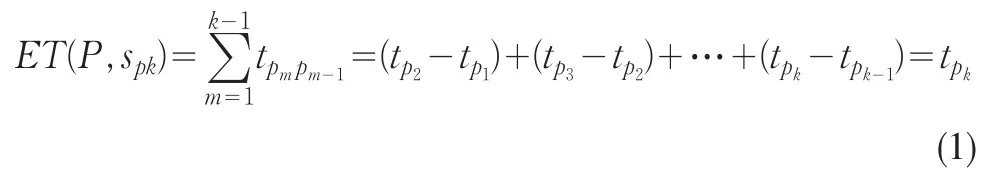
（8）扩散速度与密度：vi(ρ)表示第i个经济体的扩散速度（km/h），ρ表示扩散路径上的经济体密度（万元/km2）。

2.2 扩散模型

以上述变量为基础，建立路网规划条件下的区域多经济体动态扩散模型。

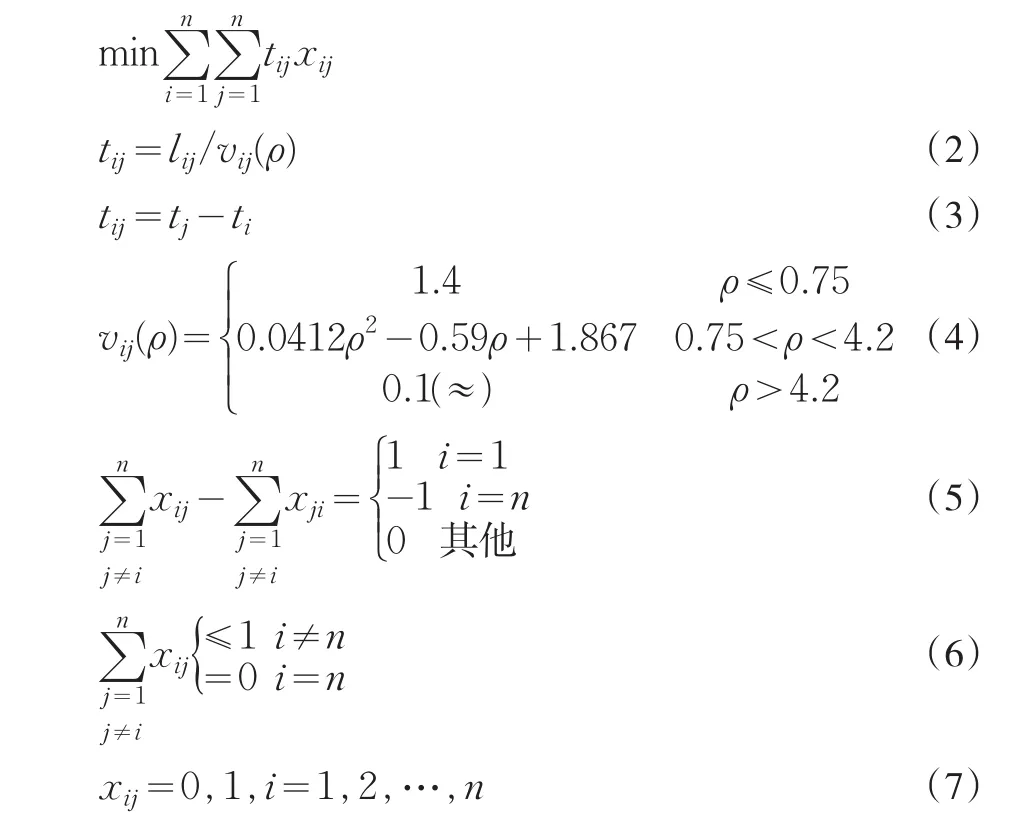
其中，式（2）、（3）为扩散时间的递推关系，即经济体在tij内以时变速度vij(ρ)通过扩散路径(si,sj)；式（4）表示各经济体在各个路径上的扩散速度；式（5）表示xij的取值构成，从核心城市s1到扩散目的地sn至少有一条可行的扩散路径；式（6）表示扩散路径中不含回路；式（7）为决策变量xij的类型约束。

为反映交通条件对经济扩散的直观影响，本模型采用核心城市与周边城镇衔接的线路长度作为路径长度的计算基础。同时，考虑到在扩散过程中，多经济体带来的相关运量分布在不同路径上可能发生的拥堵和集聚，并引起扩散速度发生变化，因此，为突出交通效应并简化计算，将相关运量统一使用经济密度（万元/km2）来表示，借用路径宽度（km）来反映运能，经济体规模（亦即对运能的占用）采用统一的单位空间产值（万元/km2/个）来表示。根据本模型的假设条件，经济体扩散速度仅具有趋势意义，不具有实际数值意义，因此借用常规流量速度来代入计算[3]。

3 模型求解

3.1 惯性权重自适应性调整粒子群算法

与遗传算法比较，粒子群优化算法的信息共享机制是很不同的。在遗传算法中，染色体共享信息，所以整个种群的移动是比较均匀地向最优区域移动。在粒子群优化算法中，只有全局极值或个体极值单项传递信息给其他的粒子，整个搜索更新过程是跟随当前最优解的过程。与遗传算法比较，在大多数的情况下，所有的粒子可能更快地收敛于最优解。

粒子群算法中的每一颗粒子代表n维空间的一个解。每一个粒子的状态为Xi=(xi1,xi2,…,xin)，粒子的速度空间向量为Vi=(vi1,vi2,…,vin)。每个粒子经历过最优的状态解集为Pi，群体的最优解集为Pg。ω为惯性权重。c1和c2为加速度常数。则t+1时刻的状态为：

3.2 求解过程

（1）编码设计：根据遗传算法中的离散和连续组合编码的优化方法，每个粒子的位置向量编码为（离散、连续变量）。其中离散变量表示N个路网节点、K个经济体的扩散问题。矩阵中的前N+k-1表示粒子的位置编码，其中的顺序为经济体的扩散顺序。矩阵的后N列表示N个路径上的经济体数目。

（2）初始解：初始解采用随机生成的方法产生。

（3）适应度计算：在解码以后，粒子的适用度采用目标函数的倒数。

区域路网规划条件下的核心城市多经济体向周边城镇扩散的动态优化问题计算流程如图1所示。

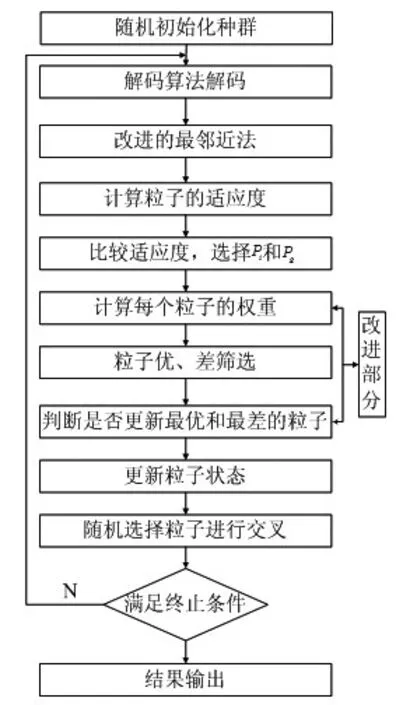
图1 经济体扩散问题求解的粒子群算法流程

4 算例

某区域为单核心城市主导区域，其中S点为该核心城市所在地，A、B、C、D、E、F分别为规划路网衔接的城镇（如图2所示）。在S点处有2385个经济体（个体产值规模为10万元/km2/个）将向这些城镇进行扩散。从核心城市到目的城镇的扩散路径分别为S-A、S-B、S-C、S-D、S-E、S-F。其中扩散路径的长度分别为S-A=40km、S-B=45km、S-C=30km、S-D=20km、S-E=25km、S-F=50km，每条扩散路径的宽度为2km。模拟结果见表1。

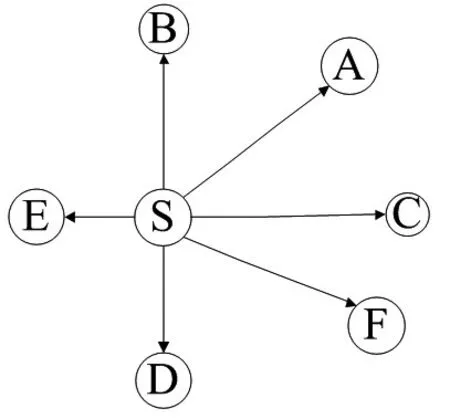
图2 区域规划路网布局

在WIN7操作系统，内存：4G，CPU：Inter P7450的环境下，通过Matlab编程，计算机上运行时间为54.5s。计算出2385个经济体从核心城市S扩散到周边城镇A、B、C、D、E、F的最优扩散方案见表1。

表1 经济体沿各路径的扩散方案

在该扩散过程中，路网中较短的路径上聚集大量的经济体，即各经济体倾向于选择扩散速度可能较快（既具有良好交通条件）的路径，较好地拟合了现实中的情景。

5 结论与展望

本文研究区域单核心城市的多经济体在路网规划引导下向周边城镇扩散的过程，建立扩散模型，并采用粒子群算法对模型进行求解。本模型的构建突出了经济个体在扩散过程中由运输和空间条件限制而产生的相互影响关系，有利于在把握经济体的博弈过程，是对当前传统的宏观分析手段的有效补充。算例证明模型和算法适用于经济扩散效应的测度，具有理论意义和实用价值。

本模型可在以下方面进一步拓展，以便更好地模拟经济扩散的过程和效果。

（1）本模型以单核心城市的区域为背景，但是真实的区域城镇分布形式可能还有多核、多层次等形式。因此，可以在本模型的基础上，增加区域核心城市的数量，并构造经济体在各层次核心城市分布的初始状态，以适应不同的区域经济空间格局；

（2）本模型假定各经济体是同质的，但是真实的经济体扩散过程可能受到产业联动关系、城镇的产业容纳能力等因素的限制。因此，根据特定区域背景，可以为本模型添加约束条件，以体现经济体之间的关联关系以及扩散路径的有限性；

（3）本模型采用核心城市路径与周边城镇衔接的线路长度表征交通条件的优劣，作为路径长度的计算基础，还可用运行时间、就业与生活的吸引机会和经济发展潜力等变量来表示交通条件所引起的阻抗，以更好地表征不同区域经济和路网构成下的扩散规律；

（4）本模型主要考虑了经济扩散的交通和空间驱动作用，但是经济体的扩散过程在速度上还受到企业扩张进程等因素的影响，在密度上还受到关联企业发展规划等因素的影响，使用常规速度密度的核算方法，虽具有定性依据，但是为更精确地反映经济扩散规律，需对这两个变量进行专题研究，建立专门反映经济体扩散的速度和密度关联公式。

[1]Peter Allen.A Sub-Regional Development Approach-Transport，In⁃ternational Trade and Investment Modeled in Space[C].SSRN Work⁃ing Paper,2001.

[2]李兴波,聂元飞,兰天.集聚视角下云南省工业地域分布与经济效应研究[J].统计与决策,2010,(4).

[3]陈曦.人员疏散速度模型综述[J].安防科技,2010,(3).

[4]聂鹏,耿技,秦志光.多路径粒子群优化自动测试用例生成算法[J].计算机集成制造系统,2012,18(1).