特质波动率与横截面收益：基于Fama-French股票组合的检验

罗登跃

（山东大学管理学院，济南 250100）

0 引言

近年来，股票特质波动率和预期收益的关系受到了国际学术界的广泛关注。经典的CAPM认为影响资产均衡价格的因素只有系统风险，投资者可以通过持有充分分散的投资组合来抵消公司特质风险，公司特质风险不影响资产均衡价格，即股票特质波动率与预期收益是无关的。

本文使用我国沪深股市1997年1月2日至2011年6月30日的AB股数据，对特质波动率与横截面收益之间的关系进行检验，原始数据来源于锐思数据库。与已有研究的最大不同在于：针对Fama-French规模-账面市值比5×5组合检验特质波动率与横截面收益之间的关系。这样做的好处是可以避免直接采用一支支股票时的信息失真问题。因为在我国股市的市场环境下，单支股票的价格往往受到操纵，其交易信息可能存在失真。另外本文还针对结果中出现的系统风险溢价为负值的情况，按照市场超额收益是否大于0将市场分为上、下市场，进行Pettengill等(1995)[1]提出的条件相关检验。

1 研究设计

1.1 特质波动率的计算

1.1.1 已实现特质波动率

特质波动率并不能直接观察到，同时对它的估计是相对于股票的系统收益的，因此它是模型依赖的。现有的特质波动率的分解方法主要有3种：Campbell等(2001)[2]基于CAPM的间接分离法；以Bali等(2005)[3]为代表的基于CAPM的直接分离法以及以Xu和Malkiel(2003)[4]为代表的基于Fama-French三因素定价模型的直接分离法。其中国内外研究中常使用Fama-French三因素模型计算特质波动率，本文也采用这种方法计算25个组合的特质波动率序列。

在每个月，对每个组合利用该月内的日数据建立三因子模型进行时间序列分析：

1.1.2 预期特质波动率和非预期特质波动率

对各组合已实现特质波动率序列分别进行P-P检验：Δyt=γyt-1+α+βt+ut，H0:γ=0（存 在 单 位 根），H1:γ＜0。其中y代表各组合已实现特质波动率。检验结果表明25个组合的已实现特质波动率均为平稳的时间序列。因此可以对25个组合的已实现特质波动率分别建立ARMA(p,q)模型来估计预期特质波动率。本文取p、q最大值为4，根据AIC准则确定最优的p、q，建立时间序列模型，然后在样本内直接采用一步向前预测得到预期特质波动率eiv，同时得到非预期特质波动率ueiv。

1.2 控制变量

为了检验特质波动率对横截面收益的影响是否是由其他因素造成的，选取控制变量。

(1)协偏度。Harvey和Siddique(2000)[5]将协偏度作为一个风险因素，证明了协偏度风险因子有显著负的风险溢价，即协偏度越高收益率越低。本文参照他们的方法度量协偏度，在每个月，对每个组合利用该月内的日数据建立如下模型进行时间序列分析：

其中的ci.t即为第i组合第t月的协偏度。

（2）前一个月的收益率。Huang等(2010)检验了Ang等(2006)提出的特质波动率之谜，发现特质波动率之谜主要是由收益率的反转效应导致的。马超群和张浩(2005)[6]发现在中国市场只有形成期和持有期在4周内的周度周期策略中存在动量异常收益。因此本文选择前一个月的收益率来控制动量效应的影响。

1.3 横截面分析模型

由于预期特质波动率在初始几个月没有对应值，本文对每一组合从1997年5月到2011年6月共170个月逐月对25个组合的超额收益与三因子的风险贝塔值、预期特质波动率以及一些控制因素进行横截面分析，得到三因子的风险溢价、特质风险溢价以及控制因素的回归系数等，完整回归模型如下：

在横截面回归得到系数γkt(k=0,1,2,3,4,5,6)的基础上，计算其时间序列的均值和方差及t-统计量来判断各个因素是否显著影响组合的横截面收益，特别是预期特质波动率的系数γ4。

2 实证研究结果

2.1 Fama-MacBeth回归结果

采用预期特质波动率、已实现特质波动率以及滞后一期的已实现特质波动率进行横截面回归分析的结果分别见表1～3。从表1～3可以得到以下几点结论：

（1）无论是否加入控制变量，预期特质波动率以及滞后一期的已实现特质波动率对组合收益都有正向的影响，但均不显著。只有当期已实现特质波动率均与收益存在显著的正相关关系。

这与一些学者的研究结论不同：邓雪春和郑振龙（2010）建立ARMA模型的方法提取预期特质波动率，研究结果表明两者之间存在显著的正向关系；左浩苗、郑鸣和张翼（2011）分别用滞后一期的实现特质波动率、GARCH（EGARCH）模型、ARMA模型估计预期特质波动率，在不加入控制变量—换手率时，预期特质波动率与预期的超额收益率之间存在显著的负相关关系，在加入控制变量—换手率时，预期特质波动率与预期的超额收益率之间仍是负相关关系，只是变得不显著；田益祥和刘鹏（2011）用EGARCH(1,1)模型估计预期特质波动率，他们的研究结果表明，预期特质波动率与股票收益率存在显著的正相关关系。

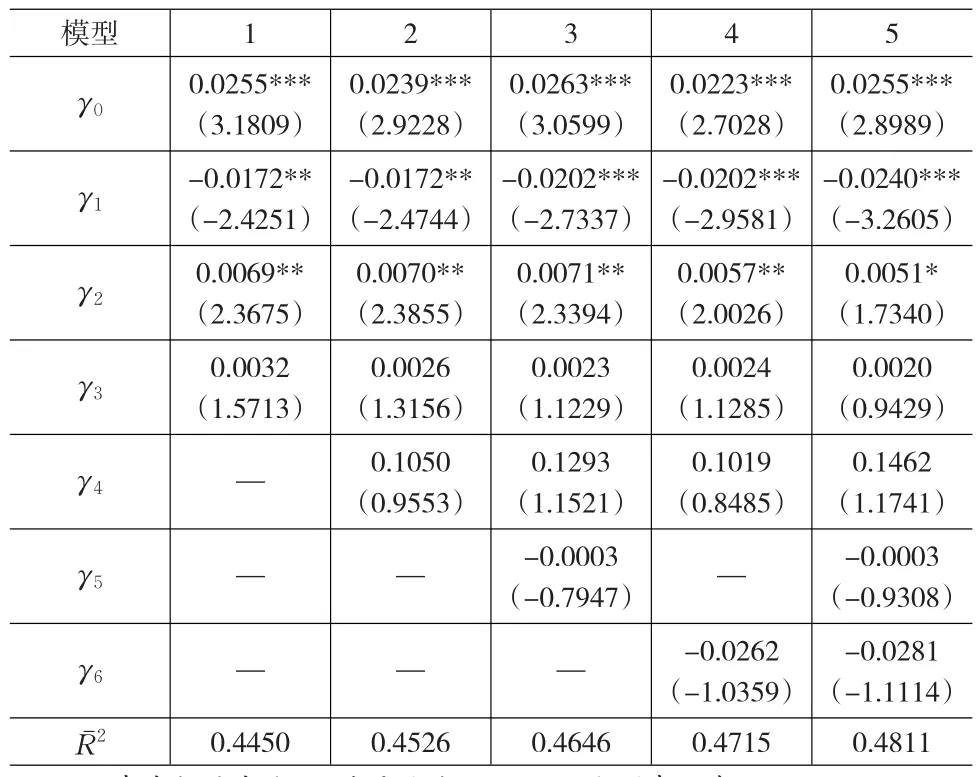
表1 预期特质波动率与收益横截面回归结果

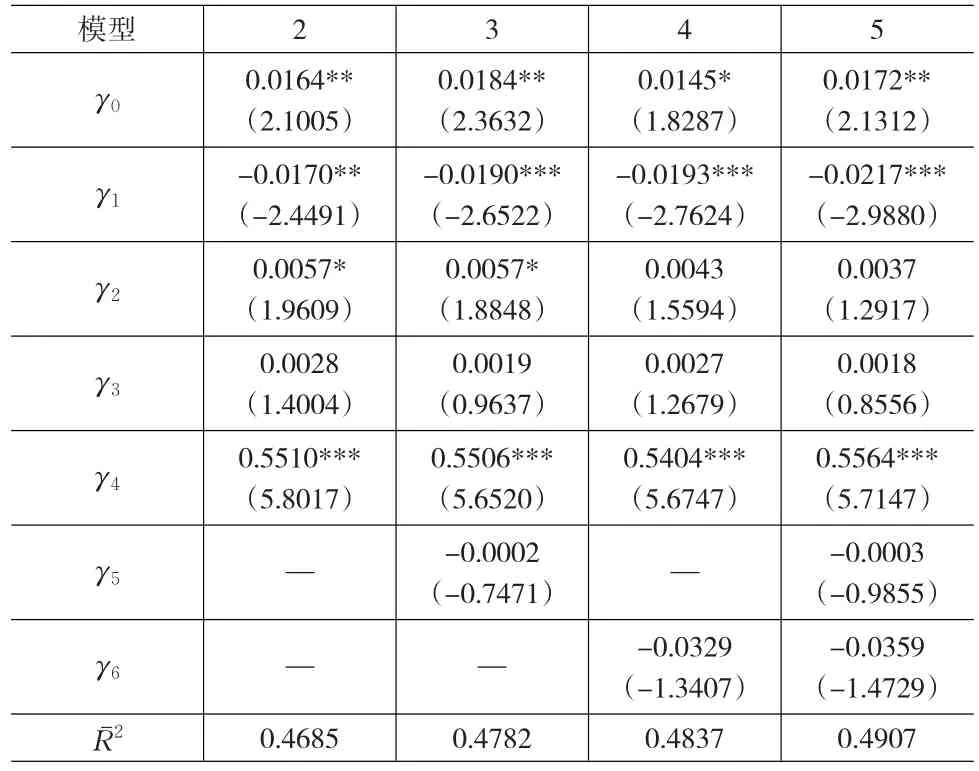
表2 已实现特质波动率与收益横截面回归结果

表3 滞后一期的已实现特质波动率与收益横截面回归结果

（2）无论是三因子模型还是分别加入预期特质波动率、已实现特质波动率、滞后一期的已实现特质波动率的模型，以及无论对收益反转和协偏度这两个因素控制与否，市场系统风险溢价均显著为负，这是与金融理论相违背的。但Miralles-Marcelo等(2012)的研究也出现了类似的情况，在他们的基准模型（CAPM和Fama-French三因子模型）、将特质波动率作为摩擦因素加入基准模型的模型以及将特质波动率作为系统风险因子加入基准模型的三个模型（加特质风险因子的模型、跨期模型和条件模型）中，市场系统风险溢价均显著为负值，只有在将特质波动率作为系统风险因子加入基准模型的标定条件模型中市场系统风险溢价为正值，且并不显著。

（3）在三因子模型、加入预期特质波动率的模型以及加入滞后一期的已实现特质波动率的模型中，规模因子的风险溢价均显著为正，但是在加入已实现特质波动率的模型中规模因子的风险溢价虽然仍为正值，但其显著性下降了或者变得不显著了。这说明当期已实现特质波动率对规模因子风险有一定的解释作用。

（4）账面市值比因子风险溢价为正，但均不显著。

（5）滞后一期的组合收益的回归系数为负值，但并不显著，表明在我国股市并不存在显著的收益反转现象。由于协偏度以及收益反转的影响均不显著，所以在后面的研究中就不再考虑这两个因素。

2.2 条件相关检验结果

前面的检验结果表明市场系统风险溢价均显著为负，这是与金融理论相违背的。Pettengill等（1995）指出由于在检验CAPM时用的是事后收益率，所以一定存在贝塔与收益的条件相关关系，即当市场收益大于无风险收益率（上市场）时，贝塔与收益正相关；而当市场收益小于无风险收益率（下市场）时，贝塔与收益负相关。风险—收益间的正相关关系成立，必须满足两个必要条件：（1）平均而言，市场超额收益应为正值；（2）上、下市场的贝塔风险溢价应该是对称的（即溢价的绝对值相等）。计算结果表明，1997年5月到2011年6月这170个月的平均市场超额收益为0.007977，大于0，满足第一个条件。但由表4可见，在上市场系统风险溢价虽然为正，但并不显著；而在下市场系统风险溢价显著为负值。因此上、下市场的贝塔风险溢价是不对称的，从而表现出前面的检验结果——市场系统风险溢价均显著为负。

2.3 非预期特质波动率

Chua等(2006)将特质波动率分解为预期和非预期的两部分，检验了非预期的特质波动率和非预期的收益率之间的关系，发现二者之间为显著的正相关。邓雪春和郑振龙（2011）在横截面回归中加入未预期到的特质波动率作为控制变量，结果表明，无论是预期的特质波动率还是未预期到的特质波动率，与收益均显著正相关。本文单独将未预期到的特质波动率加入三因子模型和同时将预期的特质波动率和未预期到的特质波动率加入三因子模型进行回归，结果表明，未预期到的特质波动率对横截面收益有显著的正向影响，在对未预期到的特质波动率进行控制的情况下，预期的特质波动率和收益存在显著的正相关关系。

表4 特质波动率与收益关系条件相关检验结果

3 结束语

本文采用1997年1月至2011年6月我国沪深股市AB股数据，基于Fama-French规模-账面市值比的5×5组合这一新视角，利用Fama-MacBeth回归法对特质波动率与横截面收益之间的关系进行了检验。研究结果表明：

(1)当期已实现特质波动率与收益呈显著正相关关系，而滞后一期的已实现特质波动率与收益的关系并不显著。

(2)非预期特质波动率与收益呈显著的正相关关系，而只有在控制了非预期特质波动率时，预期特质波动率才与收益呈显著的正相关关系。

(3)在上市场，市场系统风险与收益正相关，但不显著；而在下市场，市场系统风险与收益呈显著的负相关关系。

由于数据的局限，在进行横截面分析时无法对组合的规模、账面市值比、流动性等因素进行控制，所以得到的结论可能有一定的局限性。

[1]Pettengill,G.N.,Sundaram S.,Mathur I.The Conditional Relation be⁃tween Beta and Returns[J].Journal of Financial and Quantitative Analysis,1995,(30).

[2]Campbell,J.Y.,M.Lettau,B.G.Malkiel,Y.Xu.Have Individual Stocks Become more Volatile?An Empirical Exploration of Idiosyn⁃cratic Risk[J].Journal of Finance,2001，56（1）.

[3]Bali,T.,N.Cakici,X.Yan,X.Zhang.Does Idiosyncratic Volatility Re⁃ally Matter?[J].Journal of Finance,2005,(60).

[4]Xu Y.,B.G.Malkiel.Investigating the Behavior of Idiosyncratic Vola⁃tility[J].Journal of Business,2003,76(4).

[5]Harvey,C.R.,Siddique,A.Conditional Skewness in Asset Pricing Tests[J].Journal of Finance,2000,(55).

[6]马超群,张浩.中国股市价格惯性反转与风险补偿的实证研究[J].管理工程学报,2005,19（2）.