基于小波分析的三维Copula密度估计及其应用

彭选华

（西南政法大学经济学院,重庆401120）

0 引言

Copula理论及其金融应用前景十分广阔.Sklar(1959)[1]首次提出Copula并将其定义为把一元分布函数“连接”起来形成多元分布函数的函数.Joe(1997)[2]和Nelsen(2006)[3]系统地总结了Copula的基本性质以及Copula相关性、尾部相依性以及高维联合分布的copula藤结构等前沿问题.EmbrechtS(1998)[4]开拓性地将Copula方法引入到金融风险管理领域.随后Copula在该领域中取得了许多有价值的应用成果(Cherubini等,2004)[5]。

为此，据国内外已有研究可以推测金融变量的相依性度量简化为对随机变量潜在相依模式的最佳识别。金融变量具有复杂的统计特征，比如波动聚集性、长记忆性及分布的尖峰、厚尾等，这使得金融相依结构的局部特征非常明显，其真实Copula密度曲面可能具有参差不齐的多峰形状。由于小波函数作为局部特征识别和奇异信号处理的得力工具，具有极强的变焦功能和局部自适应能力，因此将小波引入对金融变量的相依结构度量不仅具有直观意义，还是数量金融的研究热点。为此以三维为例，考虑应用小波函数对金融变量潜在相依结构进行小波线性估值和最优化筛选。本文在给出三维Copula密度的小波线性估计量及其简洁的计算方法之后，选用DB8小波识别上证综合指数、日经225指数和标准普尔500指数等三者之间潜在相依结构的局部特征。与此同时以该估计量为基准，最小化均方积分误差筛选出最佳的混合参数Copula模型，并以此度量这三个指数在样本期内的相依结构，结果表明小波线性估计量正好弥补了参数Copula不能变焦性地展示相依结构局部特征的缺陷。

1 三维多尺度分析

小波技术已经成功地应用于不同的学科研究领域，比如信号检测、图像处理及统计学等(Vidakovic,1999)[6]。记一维尺度函数和小波函数分别为φ和ψ以及其伸缩和平移变换为：

式(6)表明小波级联分解保留了尺度之间一贯的主体趋势特征和局部异质特征。小波对相依结构的级联分解，有助于从多时间尺度方向上深度剖析随机变量之间的相依结构的变化趋势和局部细节特征。下面给出三维Copula密度的小波估计方法。

2 Copula的小波线性估计量

假设(X1,X2,X3)为三维实值随机向量，边缘分布函数分别设定为Fi(x)=Pr(Xi＜x),i=1,2,3。根据Sklar(1959)[1]定理，则(X1,X2,X3)的联合分布为：

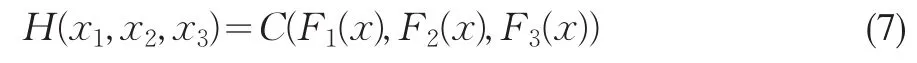
其中C为联合分布函数,边缘分布(U1,U2,U3)=(F1(x),F2(x),F3(x))∈(0,1)3为均匀分布。事实上，一般未知H的解析式，在Fi和C属于确定的分布函数簇的条件下，利用极大似然估计、两步法等经典的参数推断方法确立解析式中的参数，从C的解析式度量了三者之间的相依结构，改变其边缘分布不会影响C的函数形式。然而在未知Fi和C所属的分布函数簇时，常常利用边缘分布的经验分布对潜在Copula进行统计推断(Nelsen,2006)[3]。

假设(X1,1,X2,1,X3,1),…,(X1,T,X2,T,X3,T)是从未知分布H中抽取的T组样本，(R1,i,R2,i,R3,i)表示(X1,i,X2,i,X3,i)秩序统计量，经验分布函数为

(F1,T(X1,i),F2,T(X2,i),F3,T(X3,i))=(R1,i/T,R2,i/T,R3,i/T),i∈{1,…,T}.

易见，(R1,i/T,R2,i/T,R3,i/T)表示从C(u1,u2,u3)中随机抽取的不可观测边缘分布(U1,i,U2,i,U3,i)的样本值，容易证明C(u1,u2,u3)∈L2(R3)。由于样本的经验分布是无偏估计量，因此将其代替真实的边缘分布，对(X1,X2,X3)的Copula密度C(u1,u2,u3)进行统计推断。利用式(3)、(6)和(7)，可得：

其中尺度系数和小波系数分别为

3 计算步骤

小波给出了随机变量相依结构识别与统计推断的新方法。本文三维估计量的计算原理为：从标准化秩序统计量(R1,i/T,R2,i/T,R3,i/T)的直方图开始，运用三维小波函数对参差不齐的经验直方图逐次磨光，得到局部光滑的空间曲面，不断地调整小波分解尺度，直至获得最佳空间曲面，最后对该曲面进行规范化后作为潜在Copula的小波线性估计量。计算步骤如下：

4 实证研究

本节选取美国标普500指数(SP500)、日经225指数(N225)和上证指数(SSEC)为实证对象，其中SP500代表世界成熟股市指数，N225代表亚太地区成熟股市指数，SSEC代表新兴市场指数，时间跨度为1999年10月26日至2010年1月12日。根据Hamao等(1990)[9]的研究结论,如果两个市场中某一市场在某日没有交易,在同一实证模型中删去另一市场在该日的交易数据来进行数量分析,则不会影响研究结果的正确性。因此,为了保证交易日期的同步性,使得相依结构的小波估计量具有局部可比性,故实际平行观测样本为2132个，选用DB8小波识别三个不同性质市场指数之间潜在的局部相依结构，同时筛选出最佳的参数Copula模型。利用WavLab8.5工具箱编写程序：执行算法步骤1～5，实现对样本相依结构的小波线性估计，结果见图1～2和表1；执行算法步骤6～7，实现最优化筛选参数Copula模型，结果见表2和图3。

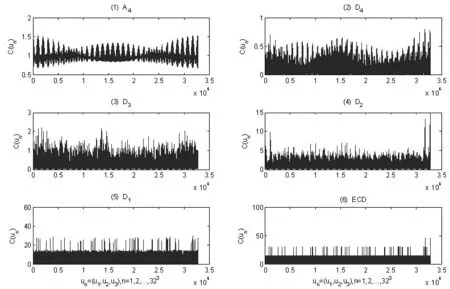
图1 三指数收益率相依结构的多尺度分析

图1是对(14)式的直观解释，其中(a)分解尺度j=1,2,3,4及网格为323个；(b)图1(1)A4表示经验Copula在分解尺度4上的趋势；图1(6)ECD表示三指数收益率之间的经验Copula；图1(2)D4表示经验Copula在分解尺度4上的局部细节；图1(3)D3表示经验Copula在分解尺度3上的局部细节；图1(4)D2表示经验Copula在分解尺度2上的局部细节；图1(5)D1表示经验Copula在分解尺度1上的局部细节。

图2 三指数收益率相依结构的多尺度级联分解

图2是对(6)式的直观解释，其中(a)分解尺度j=0,1及网格为323个；(b)图2(1)-(7)表示经验Copula ECD在分解尺度j0+1上分解成的7个细节成分；图2(8)为经验Copula在分解尺度1上的趋势；图(9)为经验Copula在分解原尺度j0上的趋势。

表1给出了不同分解尺度上小波线性估计量的均方积分误差。这些数据表明随着尺度j0增加，小波线性估计量对标普500指数、日经225指数、上证综合指数等三者之间经验Copula的估值均方积分误差越来越小，因而潜在相依结构的最佳估计量取为尺度j0=1的小波线性估计量，详见图3(8)。

表1 基于小波收缩估计量的均方积分误差 （单位：10-3）

表2给出了基于最佳小波估计量的参数Copula筛选结果及其均方积分误差(由式(15)给出)，其中c1～c6依次对应于正态N-Copula族、学生T-Copula族、冈贝G-Copula族、凯莱C-Copula族、富兰克F-Copula族和这五个族构成的混合Copula族,详见图3(1)至(6)。

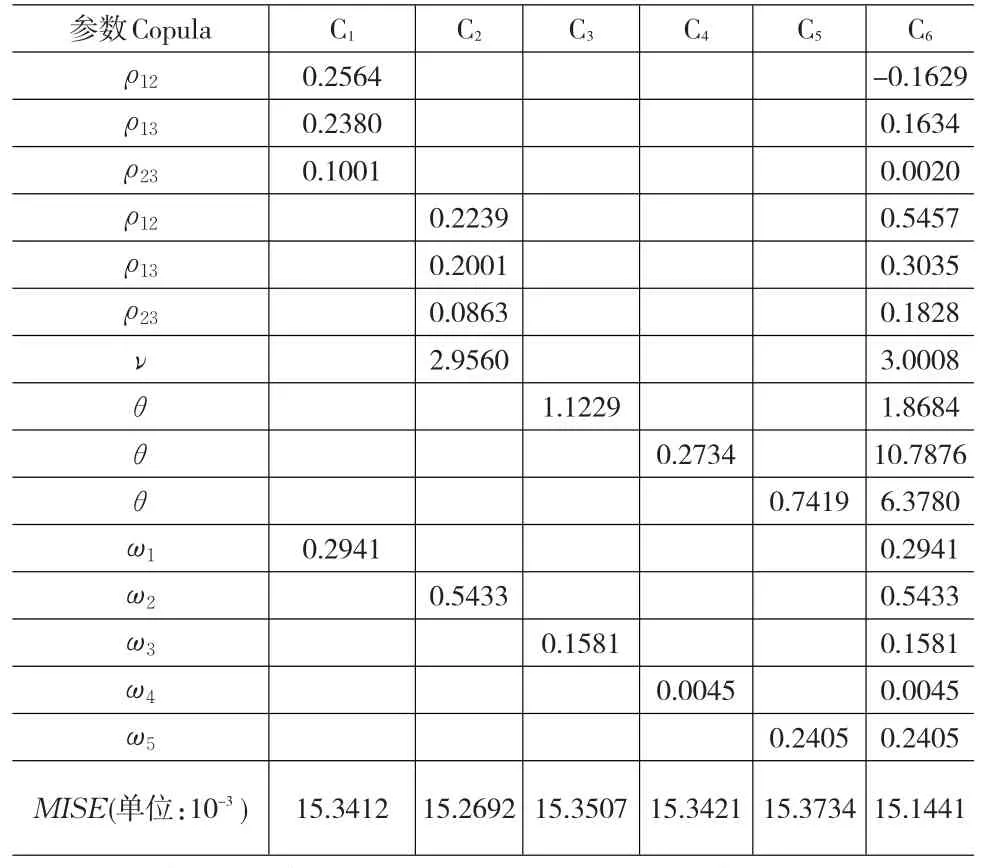
表2 基于小波线性估计量的Copula参数最优化与最小均方积分误差

表2中MISE显示每个单一参数Copula的估值误差都比混合Copula族的大，说明混合Copula族是所有参数Copula族中最好的Copula模型，用以刻画三个股市指数之间潜在相依结构特征。混合参数Copula族中对应单一参数Copula的权重度量了其对样本相依结构描述的最大贡献力度，权重还体现了混合参数Copula族内单一参数Copula之间的和谐性，从而使得混合参数Copula族中多个单一参数Copula共同增强了相依结构的建模精度。这证实了，混合Copula族整合了所有单一参数Copula族的共同优点，单一参数Copula族的最优化估值与其在混合参数Copula族的估值有明显的差异，这种差异在于后者包容了前者的不足，从而实现对样本潜在相依结构的最佳建模。

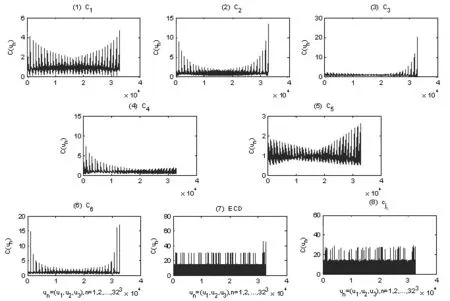
图3 指数收益率相依结构最优化的参数Copula模型

图3(8)为样本潜在相依结构在最佳尺度j0=1的小波线性估计量；图3(7)是样本的经验Copula；图3(1-6)分别是以最佳小波线性估计量为基准对参数Copula的最优化估值，顺序依次为高斯Copula、学生T-Copula、冈贝G-Copula、凯莱C-Copula、富兰克F-Copula及其混合参数Copula。

图3表明混合参数Copula是对样本潜在相依结构的最佳参数化建模。我们发现最佳的混合参数Copula清楚地展示了样本的相依结构，但视觉效果不及小波线性估计量，某些局部结构特征并不能准确地被展示出来，这是参数Copula的不足之处，然而小波线性估计量正好弥补了这个缺陷。小波线性估计量是对美国标准普尔500指数、日经225指数、中国上证综合指数等三者收益率之间相依结构的真实刻画。这为正确认识三大经济体在经济金融方面的关联性提供了一种重要的多尺度工具。

5 结论与启示

针对随机变量的相依结构建模中参数Copula估计和最佳筛选问题，本文建立了三维Copula密度函数的线性小波估计量，以最小化参数Copula与该估计量的均方积分误差为准则，筛选出最佳的混合参数Copula模型用以描述三维随机变量之间潜在的相依结构。对中美日三国的股指收益率的实证研究表明：利用Copula函数来刻画金融资产相关结构的时候,以小波线性估计量为基准更加适合在备选的参数Copula函数族中选择最优的Copula函数,该方法既可以选出与真实相关结构比较接近的混合参数Copula函数,较为真实地再现了三指数之间潜在的相依结构特征。

本文研究表明小波线性估计量具有极强的局部自适应能力。这是对潜在相依结构近乎全真地识别和重现，其尺度变焦功能体现为从不同的时间尺度展示相依结构的局部特征。因此将该方法用于多个金融市场、多个资产等之间的市场风险度量与管理也是颇有重大意义的事情。尤其应着眼于世界一体化的高度，风险管理人员及相关学者有必要利用现有的Copula技术深入研究国际金融、经济等系统变量之间的相依性结构的复杂特征及演变规律，为人类在可持续发展征途中深刻地认识清楚自身所面临的各种风险之间的联动特征，从而实现全球化的风险管理。

[1]SklarA.FonctionsdeRépartitionànDimensionsetLeursMerges[J].Pub⁃lications de l’Institutde Statistique del’Université deParis,1959,(8).

[2]Joe H.Multivariate Models and Dependence Concepts[M].London：Chapman and Hall,1997.

[3]NelsenRB.An Iintroduction to Copulas2ndEdition[M].Berlin：Springer,2006.

[4]Embrechts P,McNeil A J,Straumann D.Correlation：Pitfalls and Al⁃ternatives[J].Risk Magazine,1998,12(5).

[5]Cherubini U,Luciano E,Vecchiato W.Copula Methods in Finance[M].New York：Wiley,2004.

[6]Vidakovic B.Statistical Modeling by Wavelets[M].New York：Wiley,1999.

[7]Genest C,E Masiello,K Tribouley.Estimating Copula Densities through Wavelets[J].Insurance：Mathematics and Economics,2009,44(2).

[8]S Mallat.A Wavelet Tour of Signal Processing[M].CliforniaAcademic Press,1998.

[9]Hamao Y,Masulis RW,Ng K.Correlations in Price Changes and Vol⁃atility across International Stock Markets[J].Review of Financial Stud⁃ies,1990,(3).