随机模糊环境下供应链企业间博弈研究

刘东宝，韩东平

（1.黑龙江八一农垦大学，黑龙江 大庆 163319；2.哈尔滨工业大学管理学院，哈尔滨150001）

0 引言

伴随着知识经济以及全球经济一体化的发展，企业的经营特征以及市场环境都在发生根本性变化。作为现代竞争的主要模式，供应链对企业的发展起着至关重要的作用，处于供应链不同层级的企业充分发现，只有与其他企业建立战略合作关系，才能根据企业特点，实现优势互补，培养自身核心能力，由此更好的适应新的竞争环境。实践中，企业经营的环境就是这种充满各种不确定性因素的环境，这种不确定性是指当引入时间当引入时间因素后，事情的特征和状态不可充分的和准确的加以观察，测度和预见．在供应链上每一级节点的供应者，生产者和客户自身以及节点上下游之间产生的不确定性[1]。从供应链管理角度来看，这种不确定性主要来自六方面：供应者自身的不确定性、生产者自身的不确定性、供应链企业间合作的不确定性、客户需求的变化、供应商库存的不确定性、交货期的不确定。本文在此基础上，分析随机模糊环境下供应链企业间博弈关系，从而为企业更好的适应市场环境，加快企业发展提供参考。

1 模型的构建

本文涉及的供应链主要是从上游制造商到下游零售商之间形成的供应链，在这个供应链中，制造商以批发价销售给下层级零售商某一单种产品，然后面向顾客群体销售。销售后期对于一些未销售完的产品，零售商往往以打折方式处理掉，这个过程可能就使自身利益得到损害。所以，制造商和销售商分别决定最佳的批发价格和最佳定购批量以获取各自的最优利润。本文假定顾客需求、制造商制造成本是模糊变量，并且制造商不回收零售商未销售的产品，零售商的零售价格以及打折价相对固定，基于此，本研究构建了分散决策以及集中结构下的供应链模型：

设定制造商利润函数：

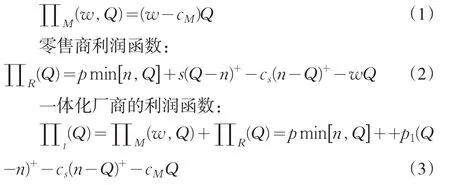
上式中各符合分别代表如下含义：

n：每期顾客需求；s：零售商对滞销产品的处理价格；cs：零售商的缺货成本；cM：制造商的制造成本；p：零售价格；w：批发价格。

实践中：n＜w≤p，此外，∏M(w,Q)、∏R(Q)分别是定义在可能性空间[θ1,P(θ1),Pos1]、[θ2,P(θ2),Pos2]上的随机模糊变量；∏I(Q)是定义在乘积可能性空间[θ1×θ2,P(θ1×θ2,Pos1∧Pos2)]上的随机模糊变量。为了更好的明确不同模糊环境下供应链企业间的博弈状况，本文分别构建了分散决策结构下的供应链模型以及集中决策结构下的供应链模型。

1.1 分散决策结构下的供应链模型

在供应链博弈中，如果制造商占主导地位，此时作为供应链上的核心企业，制造商在与零售商的Stackelberg博弈中会先做出决策，零售商据此再做出决策。具体来说，这个过程供应链制造商与零售商博弈顺序为：零售商在制造商给出产品批发价之后，会据此选择订货数量，经供应链传递，双方获得市场收益[2]。根据这一实践顺序，随机模糊环境下，建立制造商主导的两级供应链的期望值模型。

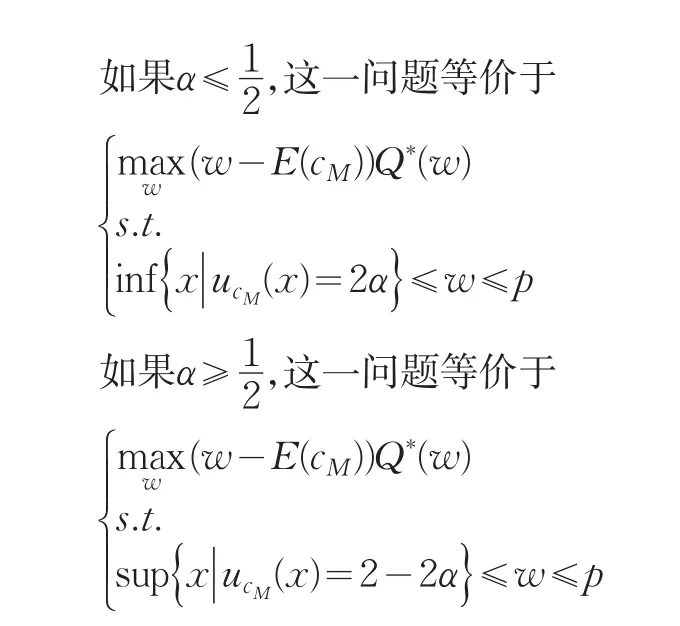
此外，E[∏M(w,Q*(w))]是关于w的连续函数，该函数在闭区间中存在最大值，制造商主导的两级供应链的期望值模型（4）的期望纳什均衡存在。

1.2 集中决策结构下的供应链模型

集中决策结构下的供应链中，纵向一体化厂商在该供应链中处于主导地位，其职能除了销售之外还涉及生产，此时可认定该供应链中制造商和经销商共同制定双赢的最优销售策略。这种情况下，两者决策不再相互影响，w将消失，E[∏IQ]是关于Q的连续函数，纵向一体化厂商可通过以下模型确定最优订货值。

2 混合智能算法

为了更好的求解本研究随机模糊模型，本文给出了一种基于PSO的混合智能算法。在粒子群算法（PSO）下，每个需要优化的问题都是一个“粒子”，通过迭代从被优化函数中找到相对应的函数值。在迭代中，该算法不仅能通过粒子本身找到最优解pbest，还能找到整个种群中的最优解。

2.1 随机模糊模拟E[∏R(Q)]

2.2 集成神经网络的随机模糊模拟的PSO算法

当上层制造商给定批发价格w时，为了减少在随机模糊模拟上的时间消耗，本文提供一种下层零售商最优利润的混合智能算法。

通过随机模糊模拟技术对n的不确定函数∏R产生输入输出数据：U:(w,Q)→E[∏R(w,Q,n)]，训练人工神经网络NN，在搜索空间内初始化微粒群，随机产生每个微粒的速度和位置[4]。

图1 混合智能算法流程图

3 模型的模拟应用

根据表1模糊语言变量和三角模糊变量的关系，可充分明确模糊变量与模糊语言变量之间的关系.在此基础上，设定制造商制造成本适中，销售期最低、最高的市场需求分别为60、75，并且p=25、cs=1.5、n=1，此时运用PSO迭代混合智能算法进行二千次的模拟，可得出本模型的数值表2。

表1 三角模糊变量和模糊语言变量间关系

表2 本模拟中供应链企业的最优决策与利润

由此可以发现，在随机模糊环境下，在供应链中处于主导地位的企业更具有竞争优势，并且制造商和零售商分散决策下的利润要少于集中决策下的利润，企业更适合采用集中决策。这一模拟结果与清新和模糊环境下的结论相一致，由此可将本模型予以拓展，应用到清晰和模糊环境下两级供应链企业间博弈研究。

4 结论

根据博弈论相关理论，在供应链中占主导地位的企业利润较大，因此，制造商和零售商在博弈中应从自身利益最大化角度出发，积极探求良好地发展对策。本文在随机模糊环境下构建的供应链企业间博弈模型以及混合智能算法，为制造商和零售商提供了良好地决策依据，以此为企业自身长远健康发展提供了理论参考和实证借鉴。

[1]C.Corbett，D.Zhou,C.Tang.Designing Supply Contracts：Contract type and Information Asymmetry[J].Management Science,2011,(50).

[2]A.Kaufmann，M.Gupta.Introduction to Fuzzy Arithmetic：Theory and Applications[M].New York：Van No Strand Reinhold,2005.

[3]关志民,潘德惠.供应链环境下供应链选择多属性组合决策模型[J].东北大学学报,2006,8(27).

[4]G.Chemo.Approximations by Super Positions of a Sigmoid Function，Mathematics of Control[J].Signals and Systems,2009,(2).

[5]聂茂林.供应链合作伙伴选择的层次变权多因素决策[J].系统工程理论与实践,2006,(3).