基于可靠性理论的被腐蚀钢筋混凝土结构维修次数优化

李 晖，滕海文，2，赵 卓，贺志远，霍 达，2

（1.北京工业大学 建筑工程学院，北京100124；2.北京工业大学 工程抗震与结构诊治北京市重点实验室，北京100124；3.郑州大学 土木工程学院，郑州450001）

确定合理的维修时间点及维修次数不仅可以延长结构的使用年限，还能够降低建筑物的日常维护成本。Nader等［1］考虑了定期或不定期的维修时间间隔对结构的影响，并通过结构的性能指标来寻求最佳的维护策略。Michael等［2］认为最佳维修时间和修复程度的确定应主要依据结构的最佳收益率。Mullard等［3］针对受腐蚀钢筋混凝土结构的维修效率进行了研究，提出以被腐蚀结构出现开裂为维修时间点为确定依据。谢桂华等［4］采用概率网络估算法对被腐蚀混凝土结构的动态可靠度及维修决策方法进行了研究。秦剑君等［5］运用群体多目标规划理论推导了建立被腐蚀结构维修策略模型的全过程。

目前，国内外针对一次性维修的优化研究较多，但由于被腐蚀结构所处的环境各不相同，各个结构的腐蚀速率也不同。对于那些长期受到严重侵蚀的结构，如果在结构服役期间仅考虑进行一次维修加固是不适合的。如何确定每个被腐蚀结构在其设计基准期内的最优维修次数就成了一个亟待解决的问题。本工作针对目前结构仅考虑一次维修加固的不足，讨论了被腐蚀结构在其服役过程中经多次维修的动态可靠度变化规律，提出了被腐蚀结构在其设计基准期内考虑维修加固处理条件下的最优维修次数的实用方法，对被腐蚀结构合理优化维修次数具有一定的理论意义和实用价值。

1 被腐蚀钢筋混凝土结构多次维修的动态可靠度衰减规律

在腐蚀性介质环境影响下，结构或构件的及抗力荷载效应均表现为一随机过程［6］。在任意一次维修时间点表现为一随机变量，假定在任意一次维修时间点（t＝tn），抗力及荷载效应均服从正态分布，则采用一次二阶矩方法［7］。计算结构n次维修的动态可靠性指标的公式为：

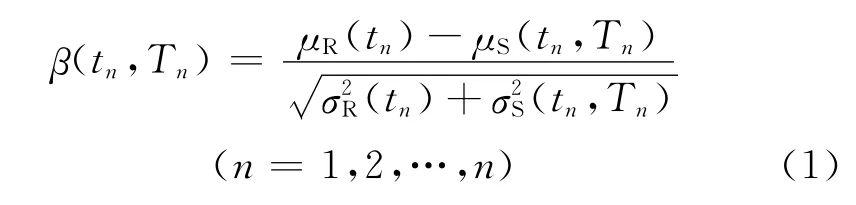
式中：β（tn，Tn）——已服役时间为tn、后续使用时间为Tn时结构的动态可靠度指标；μR（tn），σS（tn）——服役时间为tn时，结构抗力变量的均值和标准差；μS（tn，Tn），σS（tn，Tn）——服役时间为tn、后续使用时间为Tn时，结构荷载效应变量的均值和标准差。

对上述关系式进行简化，近似认为荷载效应变量的均值与方差均为常数，不随服役时间而改变，故受腐蚀结构n次维修的动态可靠度即是结构服役时间的函数。

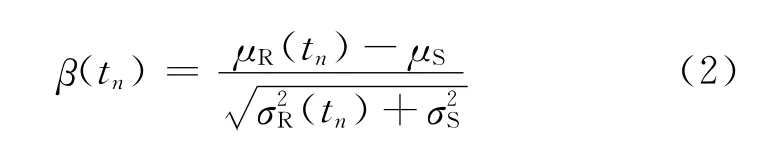
对于被腐蚀结构，其综合动态承载能力是从结构正常承载力水平开始逐渐降低的。因此被腐蚀结构从投入使用到完成设计基准期的时间区段T内，结构可靠度水平的衰减量为［8］

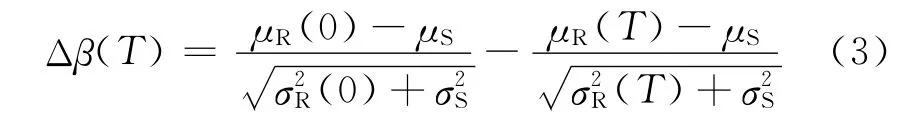
由此可见，受腐蚀结构的动态可靠度随服役时间的变化规律主要取决于结构承载能力均值和标准差随时间而变化的特点。

2 考虑多次维修条件下的优化设计

若假定在结构设计基准期内需进行多次维修，则与结构设计可靠度、多次维修的时间点、维修可靠度水平等参数完全相关。若以T表示已确定的结构设计基准期，tn表示结构多次维修的时间点，则维修目标所确定的结构后续使用时间为Tn＝T-tn。以C（0，T），（tn，Tn）分别表示结构的直接费用和多次性维修费用的总和，以表示结构n次维修所需要的时间（年），U表示正常条件下，该结构的年使用效益，则n次维修而导致的使用效益的损失为tncU，考虑n次维修情况下，被腐蚀结构总效益的优化设计与维修决策目标函数可表示为：

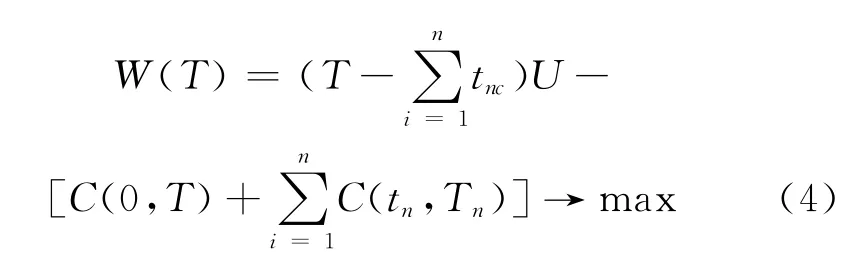
通常情况下，结构在设计基准期内的维修次数不会超过三次，当结构的维修次数n≤3时，结构的总维修时间与设计基准期相比较小，为简化计算将其忽略不计。则使上述优化目标函数取极大值等价于：

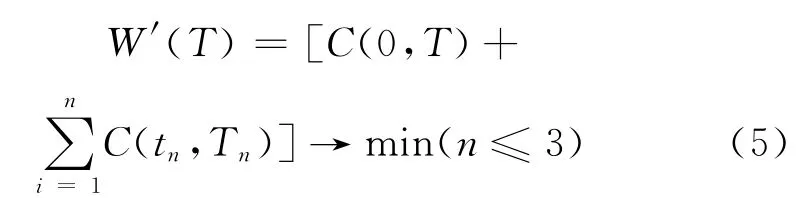
文献［9］研究并建立了设计可靠度与结构造价之间的函数关系以及结构维修费用与维修可靠度间的函数关系。

当结构设计可靠度取时，造价则可表为［9］：

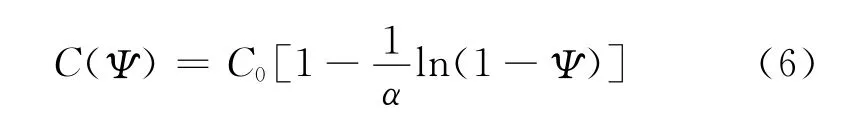
式中：C0表示结构可靠度趋近于零时的结构造价，根据近似工程经验及专家判断，对其进行大致估计。

当在时刻tn对结构进行维修，将其可靠度水平Ψn由提高到Ψ′n时，维修费用可表为：

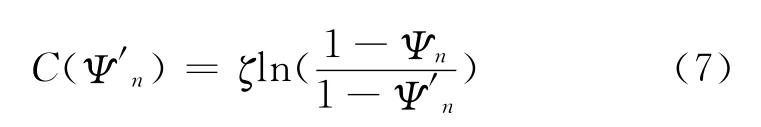
式中：ζ表示结构维修后的失效概率为维修前失效概率的0.368倍时所需要的维修费用，其值可利用综合评定和专家经验来进行评估；Ψn，Ψ′n分别表示结构第n次维修前后的可靠度水平。

上式（5）则可进一步表示为：

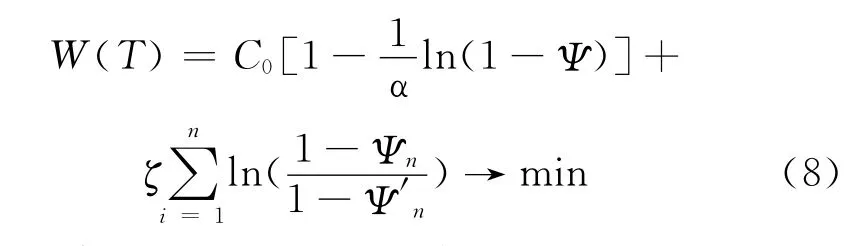
此式建立了结构设计可靠度、n次维修时刻可靠度及维修后结构可靠度与优化设计目标函数之间的显式函数关系。但由于建筑结构腐蚀过程的复杂性，使得建筑结构可靠度随服役时间的变化规律难以用简单的函数式表达，因此上式具有定性意义，如果要进行定量的优化设计还需作进一步简化。

通常情况下，建筑结构的设计基准期是由设计工艺确定的，当设计基准期内结构的维修次数分别为1次和2次时，建筑结构全过程动态可靠度水平的变化曲线分别如图1和图2所示。图中纵坐标β（t）表示在t时刻结构的可靠度水平，其为无量纲物理量，横坐标t表示结构的服役时间，其单位一般为年，也可以是天或月。β（0）表示结构在建成时的可靠度水平，然而随着结构服役时间的延长，结构可靠度水平会因外界腐蚀环境的不同而呈现出不同的下降趋势。其可靠度水平的下限值βmin可根据《建筑结构可靠度设计统一标准》（GB 50068-2001）确定。图中T表示结构的设计基准期，t1、t2表示在设计基准期内，当可靠度水平下降到βmin时结构需要进行第一次及第二次维修的时间点，Δβ（t1）、Δβ（t2）则表示结构经第一次、第二次维修后可靠度水平的提升值。

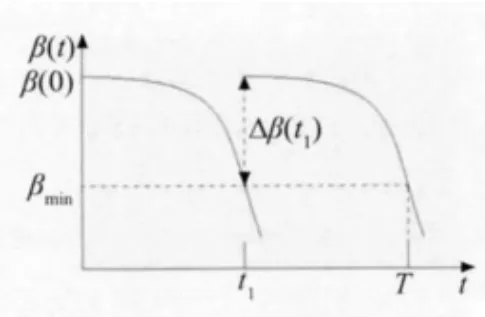
图1 一次维修条件下的动态可靠度曲线

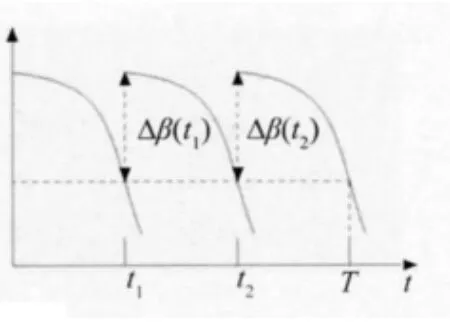
图2 两次维修条件下的动态可靠度曲线

由图可知，对结构本身而言，在其设计的基准期内要求其动态可靠度水平满足规范下限要求。图中可靠度下限值与动态可靠度变化曲线构成的封闭图形面积即是结构设计基准期内的安全裕度，其面积越大，则服役过程中结构的可靠度水平愈高，相应结构总投资额就越大。因此建筑结构优化目标函数（8）式的实质含义就是：结构在其设计基准期内，在满足规范要求的前提下，安全裕度越小，越经济。

3 受腐蚀钢筋混凝土结构维修次数的优化

动态可靠度曲线的下降速率反映了钢筋混凝土结构所受腐蚀的严重性，曲线的下降速率越大，结构所处的腐蚀环境越恶劣，所受腐蚀越严重［10］。若图1、图2中结构的设计基准期T均为50a，通过图1与图2对比可知，图2中结构的可靠度曲线在单位时间内的下降速率要高于图1，所以图2中的结构所受到的外界腐蚀要比图1严重，则图2结构的第一次维修时间点t1要早于图1，故选择进行两次维修。如果对图2结构仅考虑一次维修，则其一次维修条件下的动态可靠度曲线如图3所示。而如果对图1结构考虑两次维修，则其两次维修条件下的动态可靠度曲线如图4所示。

由图3可知，对于受腐蚀影响严重的结构，如果仅考虑一次维修方案是显然不合适的。同理对于受腐蚀影响较轻的结构，如果考虑两次维修或多次维修也会产生不必要的浪费。那么如何能够针对结构的受腐蚀情况来确定相应的维修次数就是受腐蚀结构维修次数优化的关键问题。

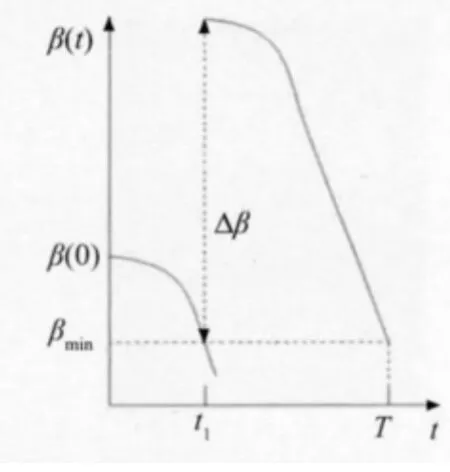
图3 严重腐蚀条件下一次维修动态可靠度曲线

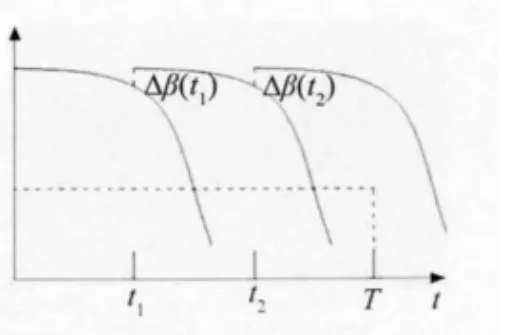
图4 一般条件下两次维修动态可靠度曲线

由图1、图2可知，在理想状态下，当β（tn）＝βmin时，动态可靠度变化曲线与可靠度下限值构成的封闭图形的面积达到最小，即此时最经济。但在实际工程中大多数情况是β（tn）＞βmin或β（tn）＜βmin。由图3、图4可知，当β（tn）＜βmin时所产生的维修费用要远大于β（tn）＞βmin时，所以受腐蚀结构维修次数的优化策略可表示为：

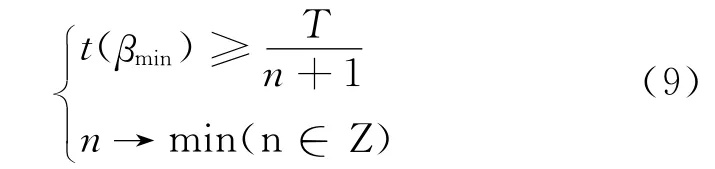
当维修次数n确定后，对维修时间点ti（i＝1，2，…，n）进行优化：

4 算例分析

在无维修条件下某钢筋混凝土框架结构在腐蚀性介质环境中工作的动态可靠度曲线如图5所示。试确定此结构在50a设计基准期内需进行几次维修加固并确定各次维修的时间点。

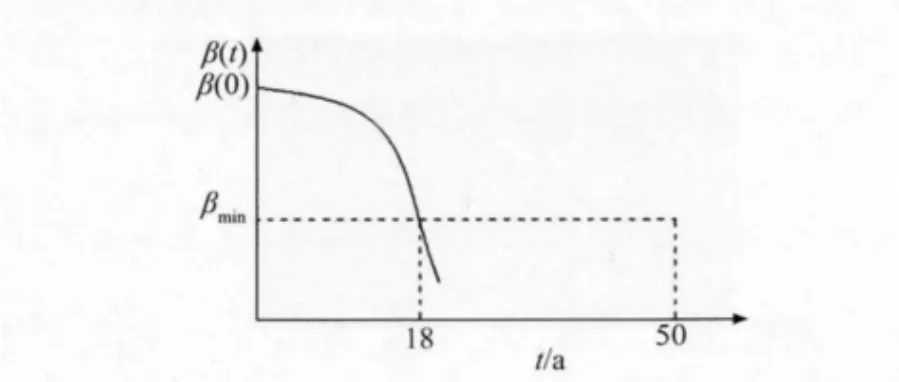
图5 无维修条件下的动态可靠度曲线

（1）结构维修次数的优化 现假设对该结构分别进行一次、两次和三次维修，即取n＝1，2，3代入（9）式。当n＝1时：

当n＝2时：

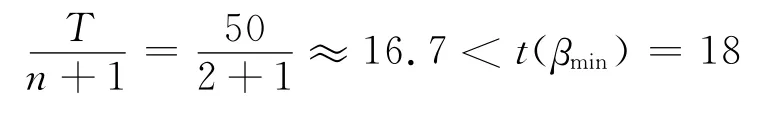
当n＝3时：

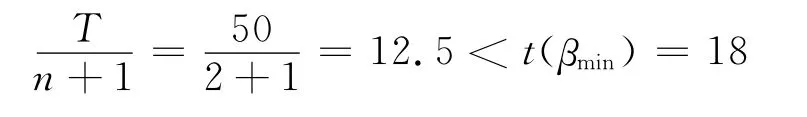
由（9）式所给条件得，即此结构在50年设计基准期内的最优维修次数为两次。

（2）结构维修时间点的优化 由（10）式得：

所以通过优化该受腐蚀结构应分别在服役18a和34a时进行维修。其优化后两次维修条件下的动态可靠度曲线如图6所示。

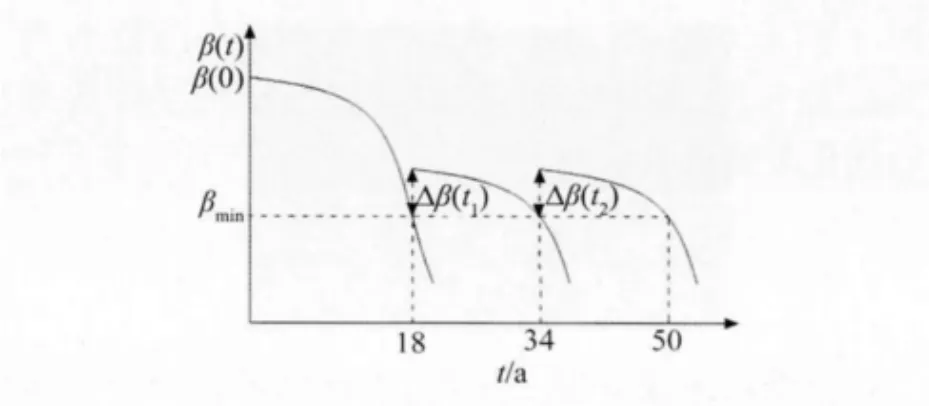
图6 优化后两次维修条件下的动态可靠度曲线

曲线与坐标轴所围面积为工程总造价。将图3与图6对比可知，若只进行一次维修，其总造价将远大于两次维修。将图4与图6对比可知，若只简单的将两次维修时间点等分于设计基准期内，又会造成不必要的浪费。所以只有选择好合理的维修次数及维修时间点，才能达到工程总造价最小的目的。

5 结论

长期处于腐蚀环境中的建筑结构，对其进行维修加固处理是使用过程中的必要环节，其设计可靠度、维修次数及维修时间点、维修可靠度水平的确定是一个复杂的全局优化问题。本工作研究了被腐蚀钢筋混凝土结构在其服役过程中经多次维修的动态可靠度变化规律，提出了被腐蚀钢筋混凝土结构在其设计基准期内确定最优维修次数的实用方法，并针对各维修时间点的确定进行了优化。该方法是全局规划问题的一种定性简化思路，对于被腐蚀严重且需进行多次维修加固的钢筋混凝土结构具有一定的理论意义和实用价值。

［1］Nader M Okasha，Dan M Frangopol.Novel approach for multicriteria optimization of life-cycle preventive and essential maintenance of deteriorating structures［J］.Journal of Structural Engineering，2010，136（8）：1009-1022.

［2］Michael Macke，Shoko Higuchi.Optimizing maintenance interventions for deteriorating structures using cost-benefit criteria［J］.Journal of Structural Engineering，2007，133（7）：925-934.

［3］Mullard J A，Stewart M G.Stochastic assessment of timing and efficiency of maintenance for corroding RC structures［J］.Journal of Structural Engineering，2009，135（8）：887-895.

［4］谢桂华，李继祥，王军.受腐蚀混凝土结构的可靠性分析及维修决策方法［J］.四川建筑科学研究，2008，34（2）：89-92.

［5］秦剑君，刘西拉，左勇志，等.结构最优可靠度的选择模型与经济收益及维修策略的影响［J］.岩石力学与工程学报，2005，24（1）：97-104.

［6］郭院成，钟维瑾，贾志尧.受腐蚀结构的动态可靠度分析［J］.郑州工业大学学报（增刊），1999：66-69.

［7］赵国藩，金伟良，贡金鑫.结构可靠性理论［M］.北京：中国建筑工业出版社，2000.

［8］郭院成，李勐勋，赵 卓.化工结构考虑一次维修时的优化设计［J］.基建优化，2000，21（5）：1-3.

［9］郭院成，霍达，赵卓.化工钢筋砼结构设计抗力水平的优化决策［J］.固体力学学报（专集），1999：232-235.

［10］吴谨.钢筋混凝土结构锈蚀损伤检测与评估［M］.北京：科学出版社，2005.